추천글 : 【화학】 화학 목차
a. 양자역학 1부
d. 양자역학 4부
1. 오비탈 원자 모형 [목차]
⑴ 오비탈(orbital) : 원자 오비탈, 분자 오비탈 등
① 넓은 의미 : 원자, 분자 등의 전자가 공간상에 존재할 확률 분포 함수. 궤도함수라고도 함
② 좁은 의미 : 그림상에 나타난 경계면은 원자핵부터 그 경계면까지 그 입자가 존재할 확률이 90%라는 의미
③ 확률 밀도는 파동함수의 제곱 ψ2으로 나타남
④ 파동함수는 슈뢰딩거 방정식으로부터 얻어짐 : 오비탈이 특정 모양을 가지는 이유는 방정식을 성립시키기 위함
⑵ 양자수(quantum number) : 양자화된 오비탈의 상태를 표시
① 주양자수 : n = 1, 2, ···으로 표시. 오비탈 크기, 전자의 에너지 준위, 전자껍질 수 등을 나타냄
○ K (n = 1인 전자껍질), L (n = 2인 전자껍질), M (n = 3인 전자껍질), ···
② 부양자수(각운동량 양자수) : ℓ = 0(s), 1(p), 2(d), 3(f), ···, n-1으로 표시. 오비탈의 3차원적 모양을 나타냄
○ 축퇴되지 않은 전자들의 에너지 상태도 나타냄
③ 자기 양자수 : mℓ = -ℓ, ···, 0, ···, ℓ로 표시. 핵 주위에서의 오비탈의 방향성을 나타냄
④ 스핀 양자수 : ms = ±1/2로 표시. 전자의 스핀 각운동량의 방향, 즉 스핀 방향을 나타냄
○ 오비탈의 위상 내지 오비탈을 구성하는 전자의 공전 방향 같은 개념
⑤ n에 해당하는 전자껍질의 양자상태는 총 2n2개가 존재
⑶ 마디(노드, node) : 전자가 존재할 확률이 0이 되는 부분
① 방사방향 마디 : 핵으로부터 방향에 관계없이 일정한 거리에서 전자가 존재할 확률이 0이 되는 표면
② 각운동량 마디 : 핵으로부터 거리에 관계없이 일정한 방향에서 전자가 존재할 확률이 0이 되는 표면
○ 오비탈 종류에 따라 각 마디의 형태와 수가 달라짐
③ 마디의 개수
○ 방사방향 마디 : n - ℓ - 1
○ 각운동량 마디 : ℓ. s 오비탈은 0개, p 오비탈은 1개, d 오비탈은 2개
○ 전체 마디 : n - 1
④ 파동함수 ψ(r)와 확률밀도함수 P(r) 간의 관계
P(r) = |ψ(r)|2 = ψ(r)ψ*(r)
⑤ 파동함수 ψ(r)와 방사 방향 확률분포함수 f(r) 간의 관계
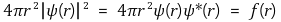
⑷ 원자오비탈(atomic orbital, 궤도함수)의 형태
① s 오비탈 (ℓ = 0) : 구형의 전자 분포를 가짐. 각마디가 없음. 1개의 오비탈을 가짐
○ 어원 : sharp orbital
○ 핵 근처(r = 0)에서 파동함수의 절대값은 최대(≠ ∞)이고, 확률밀도함수는 0의 값을 가짐
○ 예 : 2s 오비탈의 슈뢰딩거 방정식 해 (단, a0는 보어 반지름, r은 원점으로부터의 거리, c는 상수)
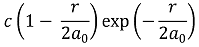
② p 오비탈 (ℓ = 1) : 아령처럼 2개의 로브를 가짐. 에너지 준위가 같은 3개의 오비탈을 가짐 (mℓ = -1, 0, 1)
○ 어원 : principal orbital
○ 두 개의 구면 중 하나의 상 부호는 (+), 반대쪽은 (-)임
○ 부호는 위상을 나타낼 뿐 전자를 발견할 확률의 대소를 의미하지는 않음
○ 상의 부호는 위상과 관련된 것으로 분자 결합을 형성할 때 나오는 보강 간섭 및 상쇄 간섭 개념과 관련 있음
○ 세 개의 p 오비탈은 x, y, z 축을 따라 배열되고 각각은 px , py , pz로 지칭
○ 핵 근처에서 전자 발견 확률이 0으로 수렴
③ d 오비탈 (ℓ = 2) : 4개의 로브를 가지며, 에너지 준위가 준위가 같은 5개(mℓ = -2, -1, 0, 1, 2)의 오비탈을 가짐
○ 어원 : diffuse orbital
④ f 오비탈 (ℓ = 3)
○ 어원 : fundamental orbital
⑤ 그 이후의 오비탈은 알파벳 순서대로 g (ℓ = 4) → h (ℓ = 5) → i (ℓ = 6) 등으로 이어짐
⑸ 원자가전자(최외각전자)
① 원자의 가장 바깥 껍질에 존재하는 전자수
② 화학 반응에 참여하는 전자들
⑹ 선택규칙(selection rule) : 전자 전이의 제한
① 주양자수 변화량 : Δn은 음수일 수도 있음
② 각양자수 변화량 : Δℓ = ±1
○ 예 : 1s → 2p는 허용되지만 1s → 2s는 허용되지 않음
③ 자기 양자수 변화량 : Δmℓ = 0, ±1
④ 스핀 양자수 변화량 : 전자는 전이할 때 스핀이 바뀌지 않음 (스핀 보존의 법칙)
⑤ Δj = ±1
2. 다전자 원자 : 바닥 상태 전자 배치 원리 [목차]
⑴ 축퇴 깨짐
① 수소꼴 원자에서는 에너지 준위가 주양자수만 결정했지만 다전자 원자의 경우 부양자수도 기여
② 원인 1. 차단효과 (shielding effect) : 전자가 많아지면 유효핵전하가 전자마다 상이
③ 원인 2. 침투효과 (penetration effect) : p 전자는 궤도 각운동량 때문에 핵에 가까이 접근 불가 → 에너지 증가
⑵ 축조원리(쌓음원리, Aufbau principle) : 오비탈에 전자가 채워질 때 에너지가 낮은 오비탈부터 채워짐
① 예시

Figure. 1. 축조원리 도식

1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d < 7p
② 주의 1. Aufbau 쌓음원리에 따르면, 4s 오비탈이 3d 오비탈보다 더 낮아 4s 오비탈에 먼저 전자가 채워지지만, 오비탈이 형성되면 3d 오비탈이 4s 오비탈보다 더 낮아 4s 오비탈부터 전자가 빠져나옴
○ 예. Fe의 바닥상태 전자배치는 1s22s22p63s23p63d64s2이고, Fe2+의 바닥상태 전자배치는 1s22s22p63s23p63d6임
③ 주의 2. d5 오비탈과 d10 오비탈은 이론이 예측하는 것보다 양자역학적 에너지가 낮음
○ 예. Cr : [Ar] 3d54s1, Cu : [Ar] 3d104s1
○ 원인 1. 4s 오비탈과 3d 오비탈은 에너지가 상당히 비슷
○ 원인 2. 4s 오비탈의 전자-전자 반발이 불안정 → d 오비탈에 나눠담는 게 안정
⑶ 파울리 배타원리(Pauli's exclusion principle)
① 한 원자에 4개의 양자수가 모두 같은 전자는 존재할 수 없음
○ 4개의 양자수 : 주양자수, 부양자수, 자기양자수, 스핀양자수
② 최대 2개의 전자가 하나의 궤도 함수를 점유할 수 있음 : 2개 전자가 있는 경우 스핀의 방향은 반대 방향
⑷ 훈트 규칙(Hund's rule) : 축퇴된 여러 오비탈이 존재할 때, 홀전자가 많을수록 안정
① 축퇴(degeneracy) : 에너지 준위가 같은 상태
② 상자성 : 홀전자가 1개 이상 있는 경우. 외부 자기장과 반응
○ 이유 : 전자의 공전은 전류이므로 외부 자기장에 의해 로렌츠 힘이 발생
③ 반자성 : 홀전자가 없는 경우. 외부 자기장과 반응하지 않음
④ 원자가 바닥상태가 아닐 경우 훈트 규칙을 만족하지 않을 수 있음
⑤ 수소꼴 원자의 경우 축퇴는 주양자수 n에 의해서만 결정
⑥ sp3d2 오비탈, 고스핀의 경우 유사 훈트 규칙이 성립함
3. 원자가결합 이론(VBT, valence bond theory) [목차]
⑴ 개요 : 루이스 구조 - 원자가 전자쌍 반발이론 - 원자가결합 이론(VBT) - 분자오비탈 이론
① 정의 : 오비탈을 루이스 구조, VSEPR에 적용시킨 것
② 근사 양자 이론 (approximate quantum theory)
⑵ 가정 : 한 원자의 서로 다른 오비탈이 결합을 위해 축퇴된 혼성오비탈이 되는 것
① 보충 : 한 원자 내의 원자가오비탈은 파동의 성질을 가지므로 섞일 수 있음
⑶ σ 결합, π 결합
① 원자가결합 이론부터 σ 결합, π 결합의 개념이 도입되기 시작
② σ 결합 : 결합축(bonding axis)을 포함하는 nodal plane이 없는 결합
○ 예 : s-s, s-p, pz-pz
③ π 결합 : 결합축(bonding axis)을 포함하는 nodal plane이 있는 결합
○ 예 : px-px, py-py
④ σ 결합과 π 결합의 결합세기
○ nodal plane이 없는 σ 결합은 결합이 세고, nodal plane이 있는 π 결합은 결합이 약함
○ 단일결합 : σ 결합 1개. 결합의 이득이 있어야 하므로 항상 σ 결합
○ 이중결합 : σ 결합 1개, π 결합 1개. 결합세기가 단일결합의 2배가 되지 못함
○ 삼중결합 : σ 결합 1개, π 결합 2개. 결합세기가 단일결합의 3배가 되지 못함
○ π 결합은 결합세기가 약해 가까워야 함 → 3주기 이상의 원자부터 좀처럼 다중결합이 관찰되지 않음
○ C, N, O는 다중결합이 쉽게 형성
⑷ sp3 혼성오비탈 : 정사면체 (예 : ethane)
① 3개의 p 오비탈이 혼성화되어 정사면체의 배향을 만듦
② 수식을 통해 h1 ~ h4 오비탈의 모양을 직접 확인해볼 수 있음
○ h1 오비탈 : ½ (s + px + py + pz)
○ h2 오비탈 : ½ (s + px - py - pz)
○ h3 오비탈 : ½ (s - px + py - pz)
○ h4 오비탈 : ½ (x - px - py + pz)
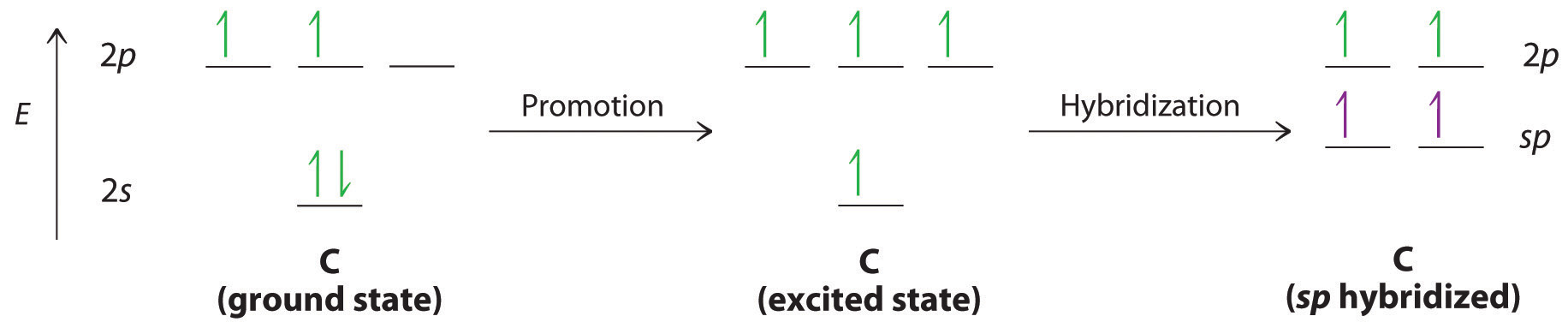
③ 예 : CH4
○ (initial) C 원자의 오비탈 : 2s2 2px1 2py1 2pz0 → 결합가지가 2개이므로 부적합
○ (promotion) C 원자의 오비탈 : 2s1 2px1 2py1 2pz1 → p 오비탈이 각 축에 놓이므로 모양이 부적합
○ (hybridization) C 원자의 오비탈 : 2h11 2h21 2h31 2h41 → 결합가지 4개. 모양 예측도 적합
⑸ sp2 혼성오비탈 : 정삼각형 (예 : ethene)
① 이중결합에서 하나는 σ 결합, 다른 하나는 π 결합
② 두 개의 p 오비탈이 혼성화되어 정삼각형의 배향을 만듦
⑹ sp 혼성오비탈 : 선형 (예 : ethyne, 이산화탄소)
① 삼중결합에서 하나는 σ 결합, 다른 두 개는 π 결합
② 한 개의 p 오비탈이 혼성화되어 선형의 배향을 만듦
③ 예 : acetylene
4. 분자오비탈 이론(MOT, molecular orbital theory) [목차]
⑴ 개요 : 루이스 구조 - 원자가 전자쌍 반발이론 - 원자가결합 이론 - 분자오비탈 이론(MOT)
① 원자가결합 이론의 한계
○ 가정 : 원자가전자가 개별 원자에 편재
○ 한계 1. 분자의 상자성·반자성을 예측할 수 없음 : 루이스 구조는 O2를 반자성이라 예측하나 사실은 상자성
○ 실제 산소는 상자성이고, MOT에 의해서만 산소의 상자성을 일으키는 홀전자가 예측됨
○ 한계 2. 결합의 benefit을 예상할 수 없음 : 예를 들면, 비활성기체는 왜 결합하지 않는가?
② 특징
○ 완전 양자 이론 (full quantum theory)
○ 모든 원자가전자가 전체 분자에 비편재
⑵ 단순화 : LCAO-MO(linear combination of atomic orbital - molecular orbital)
① 정의 : 원자오비탈 간의 선형 겹침(linear combination)에 의해서 분자오비탈이 형성된다고 보는 근사법
② 가장 널리 알려진 분자 궤도함수 근사법
③ 분자를 구성하는 원자 오비탈 간의 더하기, 빼기 조합으로 분자 오비탈을 나타내는 근사법
④ 분자오비탈 수 = 분자를 이루는 원자들의 원자오비탈 수의 합
⑤ 원자들의 전자수 = 분자오비탈에 채워지는 전자수
⑶ 분자 오비탈 총론
① 결합에 기여하는지에 따른 분자 오비탈 종류
○ 종류 1. 결합 오비탈(BO, bonding molecular orbital) : 원자 오비탈보다 에너지 준위가 낮은 오비탈
○ 원자 오비탈의 위상이 같으면 보강간섭을 하여 결합 오비탈을 형성함
○ bonding 간 상호작용과 관련
○ 예 : ψσ = ψA1s + ψB1s
○ 종류 2. 반결합 오비탈(ABO, anti-bonding molecular orbital) : 원자 오비탈보다 에너지 준위가 높은 오비탈
○ 원자 오비탈의 위상이 다르면 상쇄간섭을 하여 반결합 오비탈을 형성함
○ 오비탈에 전자가 채워져 결합 시 생기는 반발력과 관련
○ node가 있어 결합을 방해하는 요인이 있음
○ 예 : ψσ* = ψA1s - ψB1s
○ 종류 3. 비결합 오비탈(NBO, non-bonding molecular orbital) : 원자 오비탈과 에너지 준위가 같은 오비탈
② 결합의 형태에 따른 분자 오비탈 종류
○ σ 오비탈(시그마 결합) : 결합축(bonding axis)을 포함하는 nodal plane이 없는 결합 및 반결합 오비탈
○ 예 : 1sA + 1sB → σ1s + σ1s*
○ 예 : 2sA + 2sB → σ2s + σ2s*
○ π 오비탈(파이 결합) : 결합축(bonding axis)을 포함하는 nodal plane이 있는 결합 및 반결합 오비탈
○ 예 : 2px + 2px → π2px + π*2px
○ 파이 결합은 일반적으로 혼성화하지 않은 p 오비탈의 겹침
○ 파이 결합은 반드시 시그마 결합과 같이 형성 (∵ 결합의 이득이 있어야 하므로)
○ 시그마 결합이 이중으로 형성되기보다는 파이결합이 형성 (∵ 전자반발)
○ π 결합이 깨지면 너무 불안정해지므로 다중결합은 회전하지 않음
○ 3주기 이상의 원소들은 거리가 멀어 π 결합이 형성되기 힘듦 → 이중결합이 드묾
③ LUMO와 HOMO
○ LUMO(lowest unoccupied molecular orbital) : 전자가 비어 있는 오비탈 중에서 가장 낮은 에너지 준위의 분자 궤도
○ HOMO(highest occupied molecular orbital) : 전자가 채워져 있는 오비탈 중에서 가장 높은 에너지 준위의 분자 궤도
○ band gap energy : LUMO와 HOMO의 에너지 차이
○ 바닥상태에서 이에 해당하는 빛을 쏘면 전자 전이
○ LUMO가 HOMO보다 에너지 준위가 높음
④ 결합 차수
○ 결합 차수 = (결합 전자 수 - 반결합 전자 수) / 2
○ 비결합 오비탈에 배치된 전자는 결합 차수에 영향을 주지 않음
○ 결합 차수가 클수록 결합 거리가 짧고 결합 에너지가 큼
○ 결합길이, 결합세기를 비교할 때는 결합 차수를 비교해야 함
⑤ 분자오비탈의 노드 수 : 팁. 직접 그려보면 됨
○ σ2s는 0개, σ2s*는 1개
○ σ2p는 2개, σ2p*는 3개
○ π2p는 1개, π2p*는 2개

Figure. 4. 분자오비탈의 노드 수
⑥ 이온화 에너지와 전자친화도
○ 전자가 제거되는 오비탈의 에너지 준위가 낮을수록 이온화 에너지가 큼
○ 전자가 첨가되는 오비탈의 에너지가 낮을수록 전자 친화도가 큼
⑷ 분자오비탈 전자 배치
① 원자오비탈과 동일
○ 낮은 MO부터 전자배치
○ 파울리 배타원리 : 각 MO당 최대 2개의 전자 배치
○ 훈트 규칙 : 홀전자수가 최대가 되도록 전자 배치
② 경우 1. H와 2주기 원자의 결합 (예 : z축 상에 놓여 있는 H 원자와 F 원자가 결합을 형성할 때)
○ F 원자의 2px, 2py 오비탈은 결합에 참여하지 않으므로 비결합 오비탈, HF에서 에너지 준위는 불변
○ H 원자의 1s 오비탈과 F 원자의 2pz 오비탈은 σ 오비탈이자 sp 혼성 오비탈인 두 오비탈 생성
○ σ 오비탈 중 결합 오비탈은 F의 2pz 오비탈의 기여가 높고 F의 2pz 오비탈보다 낮게 위치
○ σ 오비탈 중 반결합 오비탈은 H의 1s 오비탈의 기여가 높고 H의 1s 오비탈보다 높게 위치
○ 파울리의 배타원리에 의해 각 오비탈에는 최대 두 개의 전자가 들어갈 수 있음
③ 경우 2. 2주기 동핵 이원자 분자 : X2 꼴의 분자
○ 오비탈 에너지 준위는 원자 번호의 합이 커질수록 낮아짐
○ sp orbital mixing
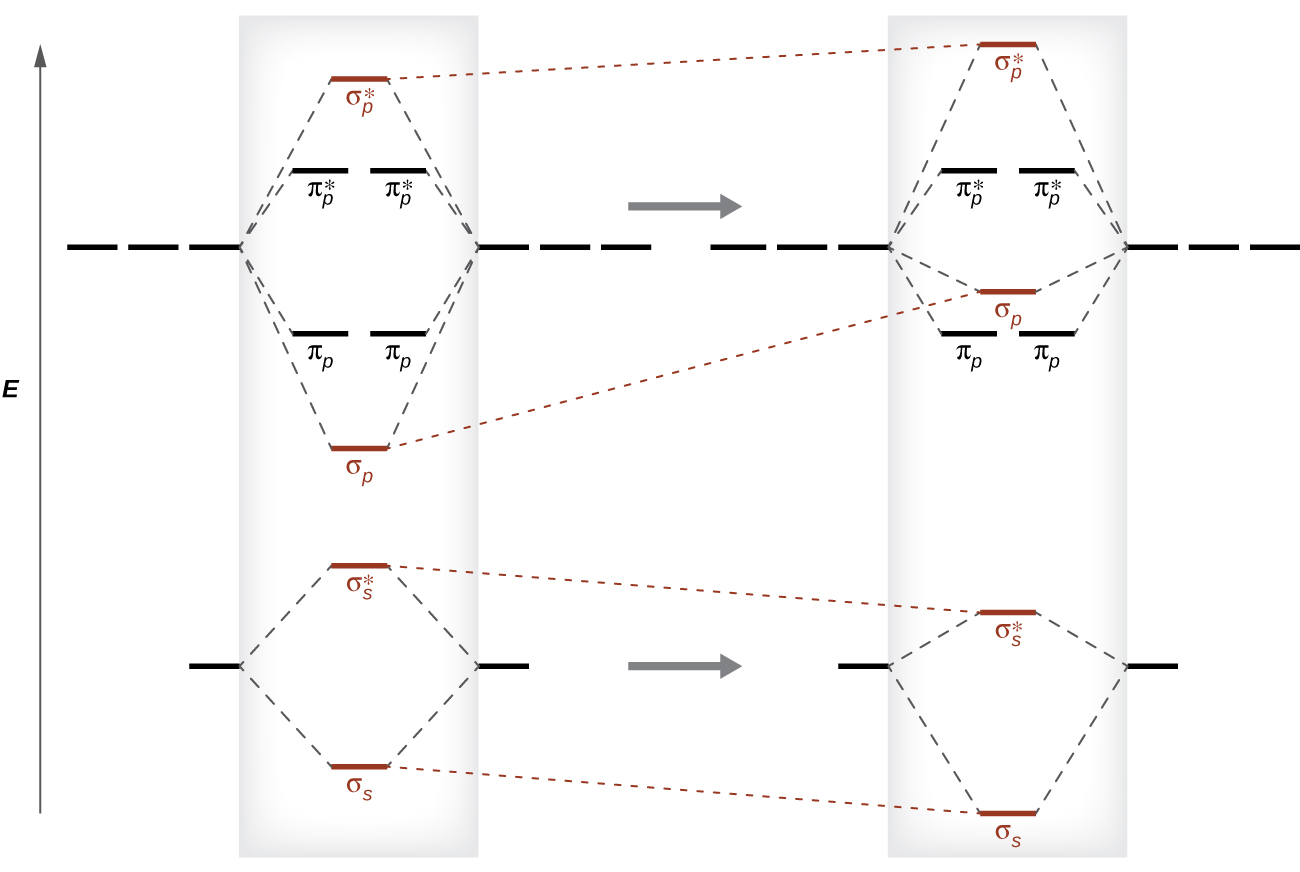
○ 2p 오비탈에서 유도된 σp 오비탈과 2s 오비탈에서 유도된 σs 오비탈은 서로 유사함
○ 서로 유사한 두 오비탈 내 전자는 파울리 배타 원리에 의해 서로 밀어냄
○ 2p 오비탈에서 유도된 σp 오비탈은 더 위로 올라가고, 2s 오비탈에서 유도된 σs 오비탈은 더 아래로 내려감
○ 2p 오비탈에서 유도된 σp 오비탈이 sp orbital mixing에 의해 πp 오비탈보다 위로 올라갈 수 있음
○ 2-1. O2, F2를 제외한 2주기 동핵 이원자 분자 : sp 혼성이 크므로 σ2p와 π2p가 뒤바뀜

Figure. 6. O2, F2를 제외한 2주기 동핵 이원자 분자의 분자 오비탈
○ 2-2. O2, F2 : sp 혼성이 없으므로 예상대로 σ2p가 π2p보다 작음

Figure. 7. O2, F2의 분자 오비탈
④ 경우 3. 2주기 이핵 이원자 분자
○ 이핵 이원자 분자의 기여도 계산
○ ψ = cAψA + cBψB
○ 1 = ∫ |ψ|2 dτ = ∫ ψψ* dτ = cA2 ∫ ψA2 dτ + cAcB ∫ ψAψB* dτ + cAcB ∫ ψA*ψB dτ + cB2 ∫ ψB2 dτ = cA2 + cB2
○ cA2 : 결합전자가 ψA에서 머무르는 확률
○ cB2 : 결합전자가 ψB에서 머무르는 확률
○ 이핵 이원자 분자의 기여도 예측 : A, B가 있을 때 B가 전기음성도가 큰 상황이라고 가정
○ B가 전기음성도가 크기 때문에 전자를 더 많이 끌어들여 에너지 준위가 낮음
○ 결합 오비탈에 대한 기여도 : A < B. (참고) 즉, 결합 오비탈에 있는 전자 밀도는 B에서가 더 높음
○ 반결합 오비탈에 대한 기여도 : A > B. (참고) 즉, 반결합 오비탈에 있는 전자 밀도는 A에서가 더 높음
○ 특정 전자의 오비탈이 A 또는 B의 특정 오비탈과 가까울 때, 그 전자는 정말 그 원자와 가깝다고 간주
○ 예 1. NO의 경우 : O2가 아닌 N2와 같은 형태의 분자 오비탈을 보임
⑤ 경우 4. polyatomic molecule에 대한 분자 오비탈
○ 3개 이상의 원자로 된 물질을 polyatomic molecule이라고 하며 MO diagram을 어떻게 그릴지가 문제가 됨
○ 4-1. H2O의 분자 오비탈
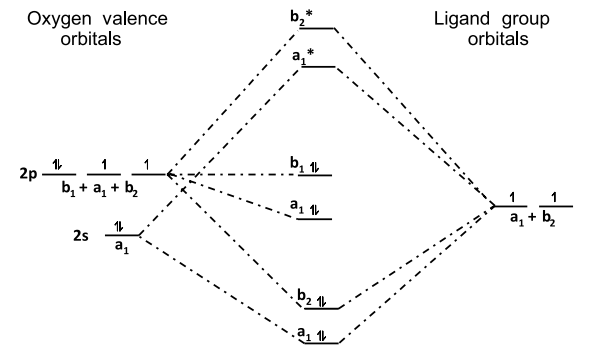
○ 4-2. NH3의 분자 오비탈
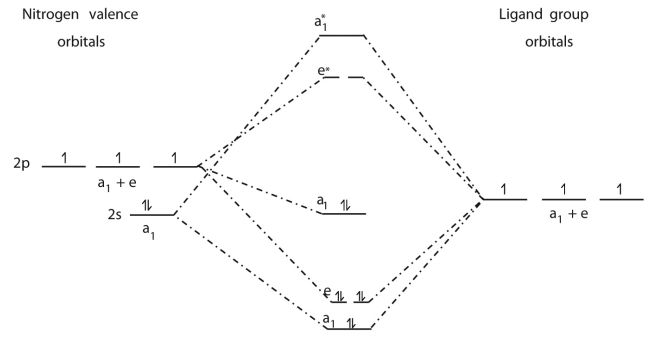
○ 4-3. BH3의 분자 오비탈
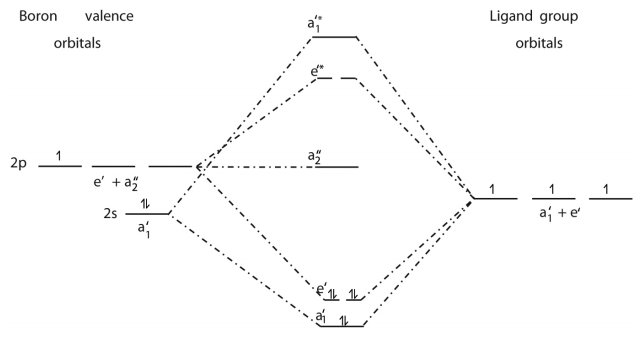
○ 4-4. SiH4의 분자 오비탈
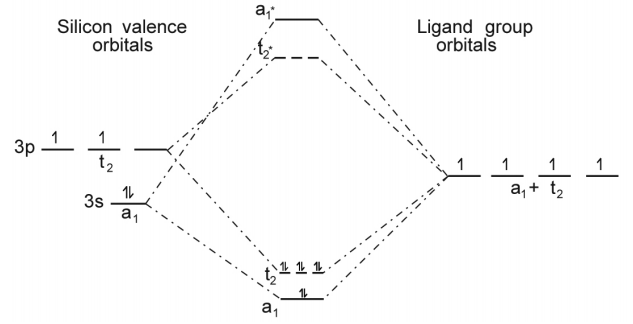
○ 4-5. CH2CHCHCH2의 분자 오비탈

Figure. 12. dien의 분자궤도함수
⑸ ► 휘켈 근사(Hückel method)
① 정의 : cyclic 혹은 acyclic polyene의 MO 에너지 및 공명 에너지를 예측하는 방법
② 기본 방정식 : | Hij - E Sij |n×n = 0 (단, | · |은 행렬식)
○ n : MO의 개수
○ 단순화를 위해, Sii = 1, Sij (단, i ≠ j) = 0이라 가정
○ Hij : i번째 탄소가 j번째 탄소 자리에 주는 영향
○ Hii = α (Columb integral). α는 탄소의 2p 오비탈 에너지 (대략 -11 eV 또는 -1100 kJ/mol)
○ Hij (단, i ≠ j) = β (resonance integral). 폴리엔의 경우 β는 대략 α의 10%
○ α, β < 0 : 음의 포텐셜 에너지를 나타냄
③ 에너지 계산
○ 전체 에너지 : 기본 방정식에서 얻어진 여러 에너지 중 가장 낮은 에너지 자리부터 MO 전자를 채운 뒤, 그 합을 구함
○ π 전자 에너지 = 이중 결합 개수 × (2α + 2β)
○ 비편재 에너지(resonance energy) = 전체 에너지 - π 전자 에너지 - 고립 전자의 개수 × α
④ 예 1. ethene
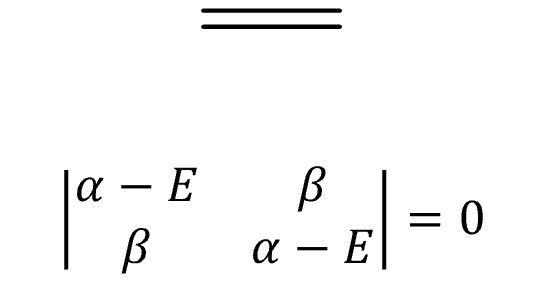
○ E = α ± β
○ MO 전자의 개수 = 2
○ 전체 에너지 = 2(α + β) = 2α + 2β
○ π 전자 에너지 = 2α + 2β
○ 비편재 에너지 = (2α + 2β) - (2α + 2β) = 0
⑤ 예 2. 1,3-butadiene
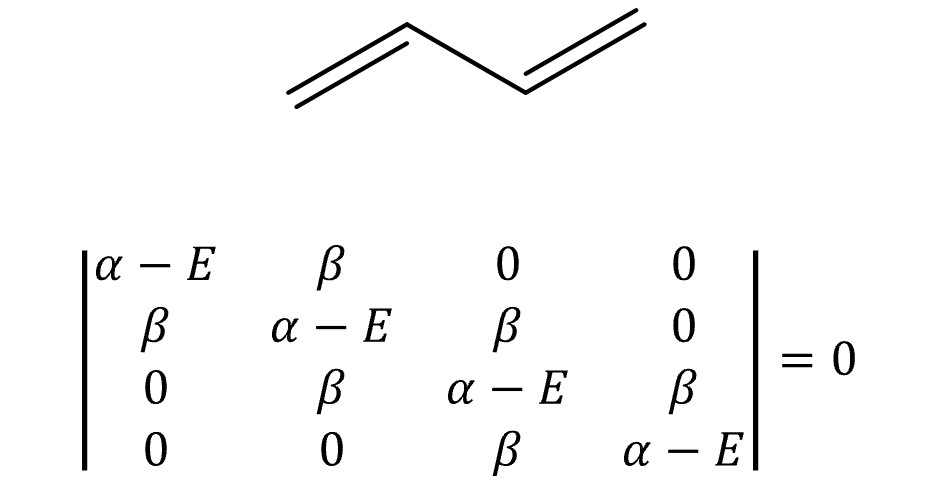
○ E = α ± 1.618β, α ± 0.618β
○ MO 전자의 개수 = 4
○ 전체 에너지 = 2 × (α + 1.618 β) + 2 × (α + 0.618 β) = 4α + 4.472 β
○ π 전자 에너지 = 2 × (2α + 2β) = 4α + 4β
○ 비편재 에너지 = (4α + 4.472 β) - (4α + 4β) = 0.472 β
⑥ 예 3. cyclopropenyl
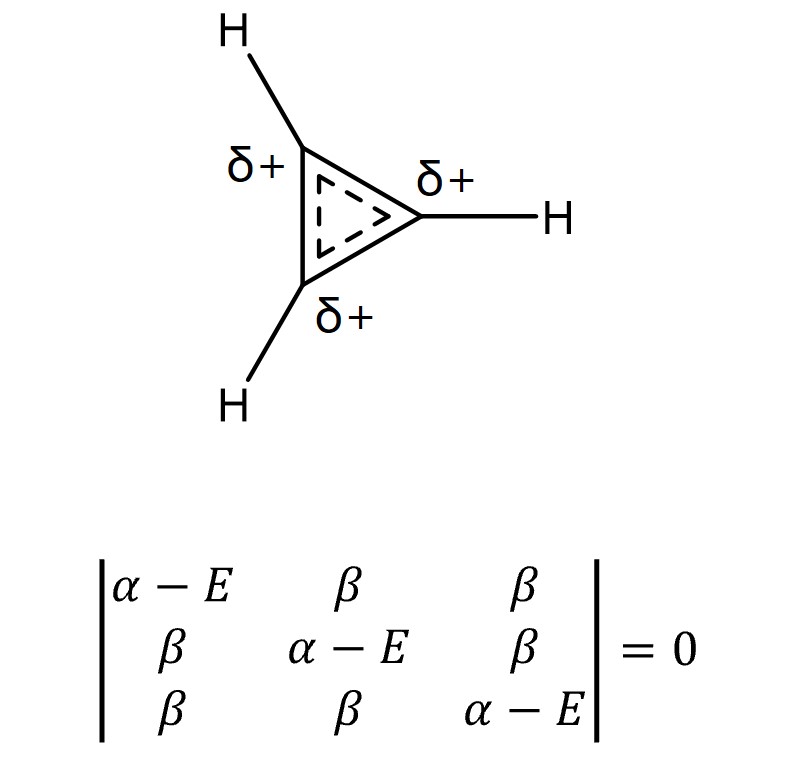
○ E = α + 2β, α – β, α – β
○ MO 전자의 개수 = 2
○ 전체 에너지 = 2 × (α + 2β) = 2α + 4β
○ π 전자 에너지 = 2α + 2β
○ 비편재 에너지 = (2α + 4β) - (2α + 2β) = 2β (∴ 방향족성)
⑦ 예 4. 벤젠(benzene)
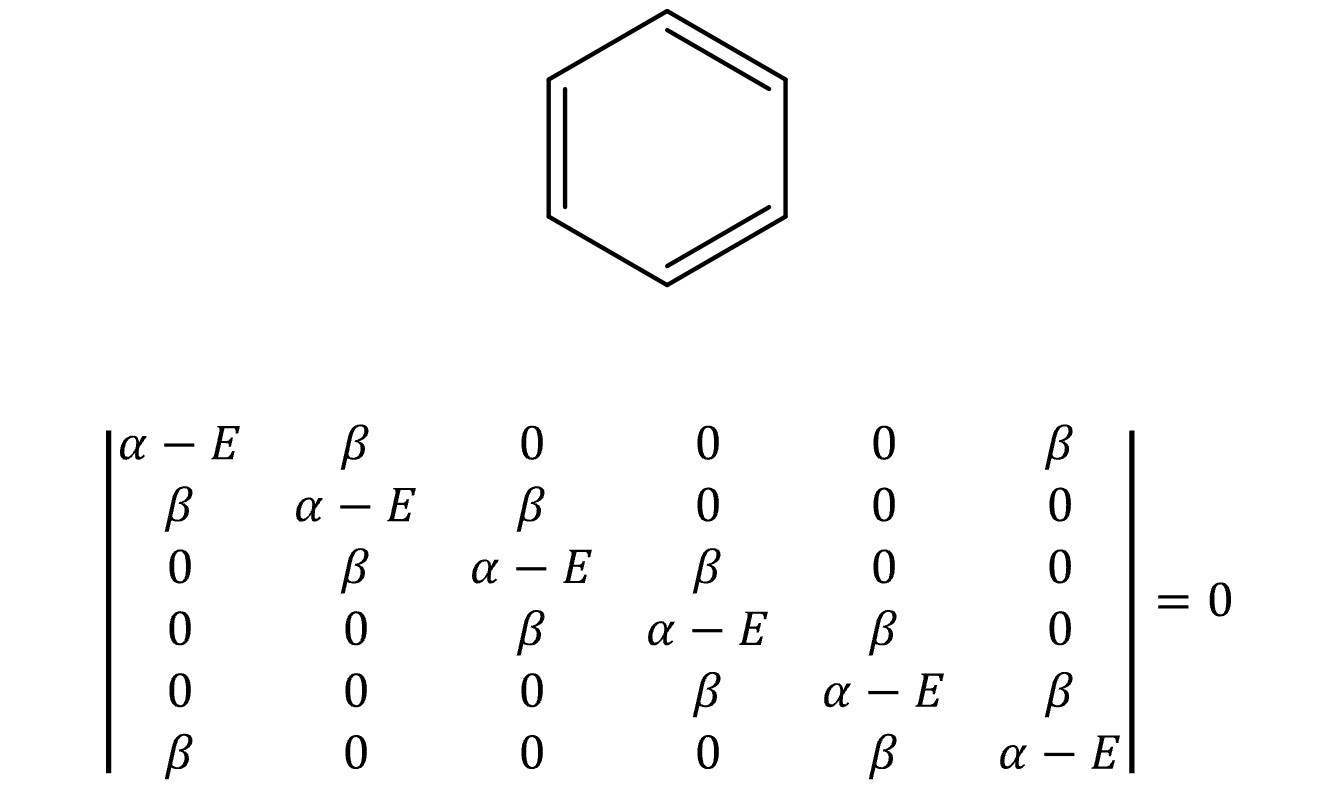
○ E = α + 2β, α + β, α + β, α – β, α – β, α - 2β
○ MO 전자의 개수 = 6
○ 전체 에너지 = 2 × (α + 2β) + 4 × (α + β) = 6 α + 8 β
○ π 전자 에너지 = 3 × (2 α + 2β) = 6 α + 6 β
○ 비편재 에너지 = (6 α + 8 β) - (6 α + 6 β) = 2 β (∴ 방향족성)
⑧ 예 5. 트라이메틸렌메테인
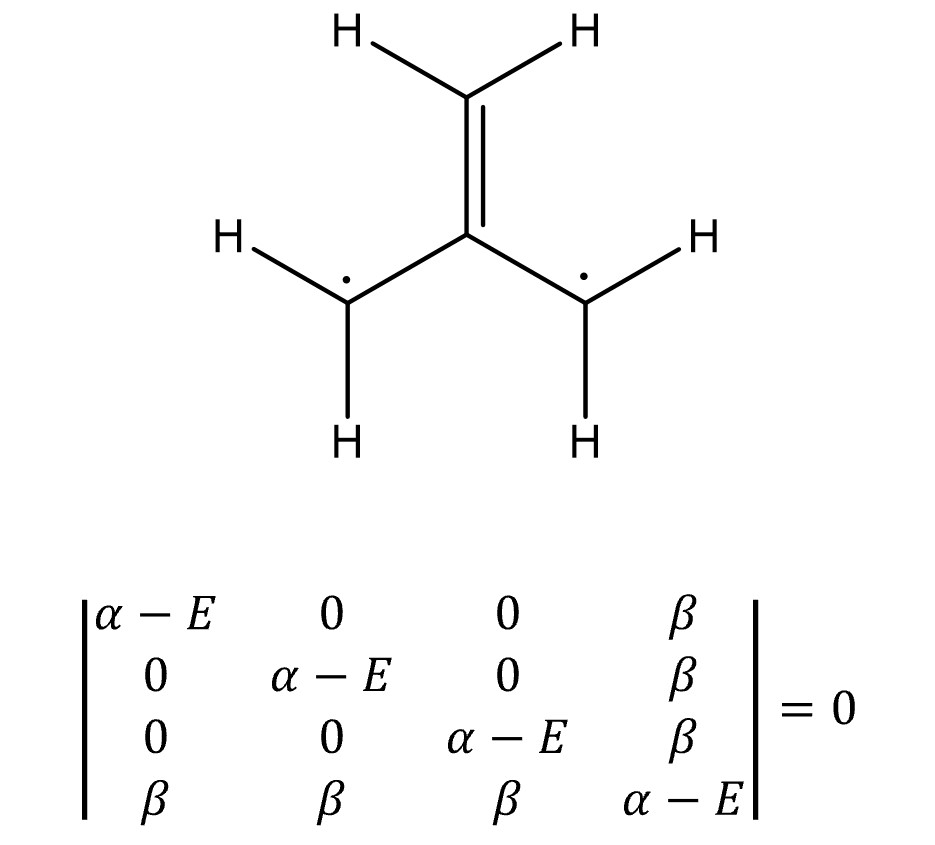
○ E = α ± √3 β, α, α
○ MO 전자의 개수 = 4
○ 전체 에너지 = 2 × (α + √3 β) + 2 × α = 4α + 2√3 β
○ π 전자 에너지 = 2α + 2β
○ 고립 전자 에너지 = 2α
○ 비편재화 에너지 = (4α + 2√3 β ) - (2α + 2β ) - 2α = (2√3 - 2)β
⑨ 예 6. 알릴 라디칼
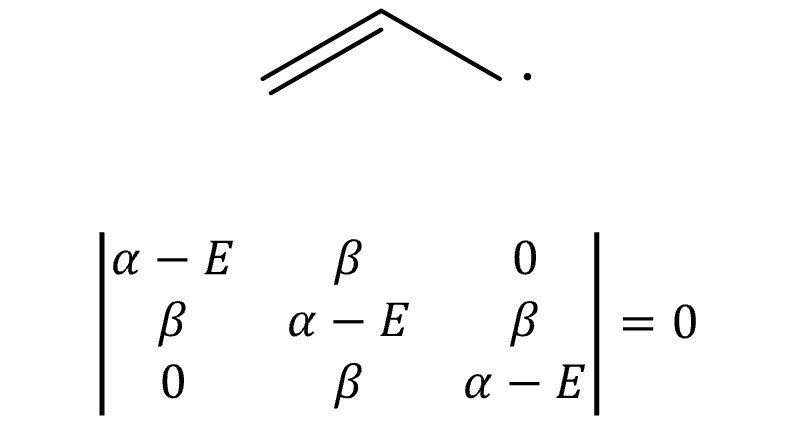
○ E = α ± √2 β, α
○ MO 전자의 개수 = 3
○ 전체 에너지 = 2 × (α +√2 β) + α = 3α + 2√2β
○ π 전자 에너지 = 2α + 2β
○ 고립 전자 에너지 = α
○ 비편재화 에너지 = (3α + 2√2β ) - (2α + 2β ) - α = (2√2 - 2)β
입력: 2019.03.02 18:22
수정: 2024.10.11 16:56
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 8강. 물질의 상태 (0) | 2018.12.27 |
|---|---|
| 【화학】 7강. 양자역학 4부 - 밴드갭 이론 (0) | 2018.12.27 |
| 【화학】 4강. 양자역학 1부 - 물질파의 도입 (0) | 2018.12.24 |
| 【화학】 3강. 원자가 전자쌍 반발 이론(VSEPR) (3) | 2018.12.20 |
| 【화학】 5강. 양자역학 2부 - 슈뢰딩거 방정식 (12) | 2018.12.20 |




최근댓글