1강. 유체의 성질
추천글 : 【물리학】 유체역학 목차
1. 개요 [본문]
2. 밀도, 비중량, 비중, 비체적 [본문]
3. 점성 [본문]
4. 압력 [본문]
5. 부력 [본문]
6. 표면장력 [본문]
7. 유체의 종류 [본문]
1. 개요 [목차]
⑴ 유체 : 아무리 작은 전단응력에도 저항할 수 없어 연속적으로 변형하는 물질
⑵ 유족 측정 기관
① 시차 액주계 (시차 정압관)
② 피토우관
⑶ 유량 측정 기관
① 관 : 벤츄리 미터, 오리피스, 로타미터
② 위어(wier) : V-놋취위어, 사각위어
2. 밀도, 비중량, 비중, 비체적 [목차]
⑴ 밀도(density) : 단위 체적당의 질량. ρ로 표시

① 압축성 유체(compressible fluid) : 밀도의 변화를 동반하는 유체
○ 예 : 일반적인 기체, 수격작용(water hammering)이나 충격파(shock wave)가 있는 액체
② 비압축성 유체(incompressible fluid) : 압축성이 없다고 가정한 유체
○ 예 : 낮은 유속으로 흐르는 기체, 일반적인 액체
③ 여러 가지 물질의 밀도
| 물질 | 밀도 |
| 공기 | 0.001 g/㎤ |
| 물 | 1.0 g/㎤ |
| 설탕 | 1.6 g/㎤ |
| 소금 | 2.2 g/㎤ |
| 알루미늄 | 2.7 g/㎤ |
| 철 | 7.9 g/㎤ |
| 금 | 19.3 g/㎤ |
Table. 1. 여러 가지 물질의 밀도
⑵ 비중량(specific weight) : 단위체적당 무게. γ로 표시
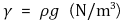
⑶ 비중(specific gravity)
① 정의 : 물의 밀도에 대한 어떤 물질의 밀도. s로 표시
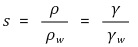
② 측정방법 : 부력의 원리, 비중병, 파스칼의 원리
⑷ 비체적(specific volume) : 밀도의 역수
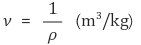
3. 점성 [목차]
⑴ 정의
① 점성(viscosity) : 끈적끈적한 정도. 분자 간 인력의 척도
② 전단변형률(deformation rate) : 속도기울기

③ 절대점성계수(absolute viscosity, dynamic viscosity) : 전단응력에 대한 전단변형률의 비례상수. μ로 표시
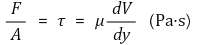
○ 차원 : μ = FTL-2 = ML-1T-1
○ 단위 : 1 poise = 100 centipose = 1 dyne·s / cm2 = 0.1 N·s / m2
④ 동점성계수(kinematic viscosity) : 절대점성계수를 밀도로 나눈 물리량. ν로 표시
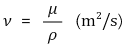
○ 차원 : ν = L2T-1
○ 단위 : 1 stokes = 1 cm2 / s = 10-4 m2 / s
⑤ 이상유체(ideal fluid) : 점성이 없는 유체
⑥ 실제유체(real fluid) : 점성이 있는 유체
⑵ 점성계수 유도 : 기체에 대한 kinetic theory에 의하면 이상기체의 경우 점도는 다음과 같이 유도됨
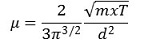
① m : 기체 분자량
② R : 기체상수
③ T : 절대온도
④ d : 기체분자의 지름
⑶ 점성계수 측정방법
① 뉴턴의 점성법칙을 적용한 점도계 : 맥미켈 점도계, 스토머 점도계
② 하겐모아젤 방정식을 적용한 점도계 : 오스트왈트 점도계, 세이볼트 점도계
③ 스토크스 법칙을 적용한 점도계 : 낙구식 점도계
⑷ 응용
① 문. 물 속에 고체의 구형 콜로이드 입자(입자크기 < 1 ㎛, 비중 = 1.20)들이 부피분율 Φ1과 Φ2로 분산되어 있을 때(Φ1 > Φ2) 어느 쪽의 콜로이드 입자들이 먼저 침전하겠는가?
○ 출처 : 이동현상의 응용과 해법, 이동현상 부문위원회(이현구), 한국화학공학회, 2002, 14 p.
② 답. 미세한 입자가 분산되어 있는 현탁액의 유효점도 μ는 입자의 부피분율 Φ가 크지 않고(즉, Φ << 1이고) 레이놀즈 수가 매우 작을 때(즉, Re << 1일 때)
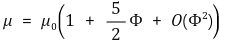
로 주어진다. 여기서 μ0는 순수한 물의 점도를 나타낸다. 따라서 Φ가 커지면 용액의 유효점도 μ가 커지면서 콜로이드 용액 내의 입자의 침강속도는 느려진다. 그러므로 Φ1 > Φ2일 때 부피분율이 Φ2로 작은 쪽의 입자가 먼저 침전한다. 또한 입자수 농도가 증가하면 입자끼리의 상호작용에 의한 hindering 효과에 의해서도 침강속도가 느려진다.
⑸ (참고) 프란틀의 혼합거리(mixing length)
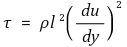
4. 압력(pressure) [목차]
⑴ 정의 : 단위 면적당 받는 힘의 크기
P = F / A
① 스칼라량으로 방향을 포함하지 않음
⑵ 단위 : N / ㎡, Pa, bar, hPa, atm, mmHg, torr, Aq
① 1 Pa = 1 N / ㎡
② 1 bar = 100 kPa
③ 1 hPa = 100 Pa
④ 1 atm = 101,325 Pa
⑤ 1 atm = 760 mmHg
⑥ 1 torr = 1 mmHg
⑦ 1 Pa = 0.00010204 mAq
⑶ 유체 표면으로부터 깊이가 h인 지점에서의 압력
① 수식화
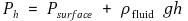
② 증명
Figure. 1. 부력 공식 증명 도식
○ 힘 표시
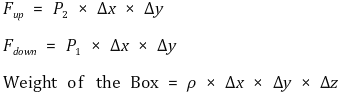
○ 힘의 평형에 의해 Fup + Weight = Fdown이 성립
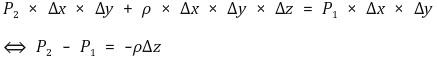
○ 만약 ρ가 상수라면 위 식을 적분해서 다음을 얻을 수 있다.
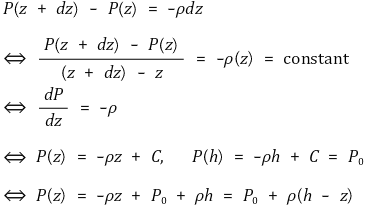
○ P(z)는 해저를 0으로 할 때 연직 z (m)에서의 압력 ↔ Pº(z)는 해수면을 0으로 연직 아래 z (m)에서의 압력
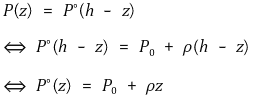
○ 만일 ρ가 상수가 아니라면 식은 다음과 같이 변형됨
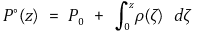
⑷ 파스칼의 원리(Pascal's Principle)
① 개요
○ 정의 : 압력은 유체 내 각 부분에 골고루 전달된다는 법칙
○ 정리 1. 임의의 한 점 압력은 어느 방향에서나 같음
○ 정리 2. 압력은 단면에 직각으로 작용
○ 정리 3. 동일 연직선상의 압력은 동일
② 증명
Figure. 2. 파스칼의 원리 증명
○ 전단응력이 없다고 가정
○ 수평힘 평형
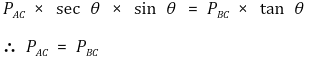
○ 수직힘 평형
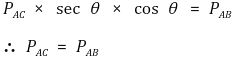
○ 임의의 수중 구조물은 무수한 삼각형의 조합으로 이뤄짐 → 임의의 지점에서의 연직방향 압력은 모두 동일
③ 힘의 이득 有, 일의 이득 無
④ 응용 : 사이펀 원리
⑸ 압력 측정기
① 마이크로 미압계 : 미세한 압력 측정
② 피에조 메터 구멍 : 교란되지 않는 정압 측정
③ 피토우관 : 동압 측정 기관
④ 브르돈 압력계 : 게이지 압력과 평형이 되게 하여 측정
○ 정확한 미압을 측정하지는 못하고 탱크 내의 가스 압력을 측정하기 위함
5. 부력(buoyancy) [목차]
⑴ 정의 : 물체가 유체에 잠겨있을 때 물체의 중력과 반대 방향으로 작용하는 힘
⑵ 크기

⑶ 유도
① 중력장 내에서 물체의 앞뒤, 좌우에 미치는 압력의 합력은 0
② 중력장에서 아래쪽 압력이 위쪽 압력보다 큼 → 힘의 합력은 아래쪽에서 유체가 물체를 들어올리는 힘 존재
③ 엄밀한 수학적 증명 : 발산정리가 사용
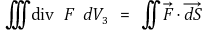
⑷ 아르키메데스의 원리(Archimedes' Principle)
① 부력의 다른 표현
② 표현 1. 유체 속의 물체는 잠겨 있는 부분의 부피에 해당하는 유체의 무게만큼 부력을 받음
③ 표현 2. 물을 가득 담은 수조에서 유체에 의한 부력은 넘친 물의 무게와 같음
④ 일화 해석
○ 순금과 가짜 금의 부피는 일정 → 순금과 가짜 금의 부력은 같음
○ 순금의 밀도가 가짜 금의 밀도보다 크므로 중력은 순금이 큼
○ 순 중력은 순금이 큼 → 수중에서 양팔저울에 순금과 가짜 금을 올려놓으면 순금 쪽으로 기울어짐
⑸ 물에 잠긴 빙하의 부피 계산 : 약 87% ~ 88.5%
① 일반적인 얼음의 밀도 : 0.9 g / ㎤
② 빙하의 얼음의 밀도 : 0.917 g / ㎤ (압축돼 있음)
③ 해수의 밀도 : 1.035 g / ㎤
④ 수식화
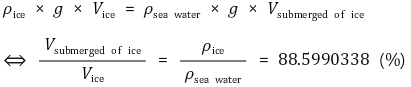
6. 표면장력(surface tension) [목차]
⑴ 정의 : 유체를 이루는 분자들이 표면적을 최소화하려는 힘
① 물방울이 둥근 이유
② 유체분자 간 인력이 클수록 강함 : 특히 물과 같이 수소결합하는 물질이 해당
⑵ 쉬운 이해
① 내부에 있는 분자는 모든 방향으로 인력이 작용해 합력이 0
② 표면에 있는 분자에 작용하는 인력의 합력은 내부로 향함
⑶ 어려운 이해
① 표면이 내부보다 포텐셜이 높음
② ①에 의해 표면에 있으려는 분자수를 최소로 하려고 함
③ ②에 의해 표면적을 낮추려는 힘이 작용
⑷ 라플라스-영(Laplace-Young) 식 : 표면장력의 크기를 기술
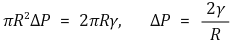
⑸ 현상 1. 액체 막의 확장
Figure. 3. 액체 막의 확장과 표면장력
액체 막의 크기는 과장되었다.
분자 간 인력의 평형상태인 2, 3번 입자는 저항력을 생성하지 않는다.
그러나 1번 입자는 ← 방향의 알짜 합력을 받는다.
왜냐하면 다른 액체들이 끌어 내리려고 하기 때문이다. (V 표시)
1번 입자들을 연결하면 하나의 선을 이루므로 표면장력은 표면적이 아니라 길이에 비례한다.
F = 2 × b × σs + F마찰, 운동이다. (단, 폭은 무시한다.)
계수 2는 막이 2쪽이 있어서 가장자리도 2개이기 때문이다.
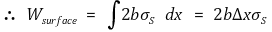
⑹ 현상 2. 액체 위에 떠 있는 동전 : 소금쟁이의 예
Figure. 4. 액체 위에 떠 있는 동전
이 경우 동전 아래의 입자는 힘의 평형으로 들어올리는 힘이 없다. (즉, 수직항력 = 0)
모서리 부분의 물 분자가 각 θ만큼 경사진 부분의 물 분자에 의해 당겨진다; 그 힘으로 동전이 들어 올려진다.
⑺ 현상 3. 모세관 현상와 매니스커스
① 모세관 현상(capillary action)
○ 정의 : 유체가 가느다란 관과의 인력으로 유체 기둥을 형성하는 것
○ 접착력(adhesion) : 서로 다른 물질 간의 인력
○ 응집력(cohesion) : 같은 물질 간의 인력
② 매니스커스(maniscus)
○ 모세관의 유체기둥의 표면 형태
○ 물의 매니스커스 : 물-실험관의 부착력이 물-물 응집력보다 크므로 ∪자 모양의 매니스커스 형성
○ 수은의 매니스커스 : 수은-실험관의 부착력이 수은-수은 응집력보다 작으므로 ∩자 모양의 매니스커스 형성
⑻ 접촉각(안식각, contact angle)
① 정의 : 접촉점에서의 접선과 고체면이 이루는 각
② 접촉점에서 힘의 합력은 0임
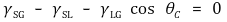
③ 적심성(wettability)에 따른 물질의 분류
○ θ = 0° : 친수성(hydrophilic)
○ 0° < θ < 90° : 부분 친수성
○ 90° < θ : 소수성(hydrophobic)
④ 임계 표면장력(critical surface tension)
○ 정의 : 접촉각이 0이 될 때 액체의 표면장력 γLG. 즉 γLG의 최솟값. Zisman이 제안
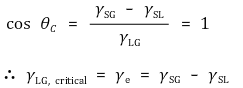
○ 1st. 한 표면에 서로 다른 표면장력을 가진 액체의 접촉각을 측정
○ 2nd. γLG - cos θ 그래프를 플롯
○ 3rd. 그래프를 선형 추세선으로 연장하여 θ = 0일 때의 γLG를 추산
○ 중요성 1. 재료 고유의 성질
○ 중요성 2. 임계 표면장력을 통해 접촉각을 예측할 수 있음

⑤ 접촉각 측정 방법 : 정접촉각 측정방법, 동접촉각 측정방법
⑥ 접촉각으로부터 표면에너지를 구하는 방법
○ 1st. 접촉각을 측정
○ 2nd. dispersive component와 polar component를 구함
○ 3rd. Owens-wendt 표면에너지를 계산
⑼ 계면활성제 : 표면장력을 낮춤
① 강한 계면활성제 : 비누, SDS, Triton X
② 약한 계면활성제 : bile salt
7. 유체의 종류 [목차]
⑴ 유체의 멱법칙 모델(power law model)
① 유체가 z-축으로 흐르고 있다고 가정
② 유체의 운동방정식은 다음과 같은 멱법칙에 의해 지배받음
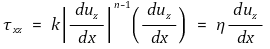
○ τ : 전단응력 (Pa)
○ k : 점조성계수(consistency coefficient) (Pa·sn)
○ η : 유동거동지수(flow behavior index) 또는 겉보기 점도(apparent viscosity)
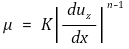
○ 전단속도(shear rate)
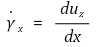
⑵ 종류 1. 뉴턴 유체(Newtonian fluid) (예 : 물, 공기 등)
① 정의 : 응력에 관계없이 점성이 일정한 유체. n = 1인 경우
② 전단응력과 속도구배가 선형적
③ 관류에서의 속도분포가 포물선형을 가짐
⑶ 종류 2. 비뉴턴 유체(non-Newtonian fluid)
① 종류 2-1. 시간 독립성 거동 유체(time-independent behavior fluid) : 유체의 멱법칙 모델을 잘 따름
② 종류 2-2. 시간 의존성 거동 유체(time-dependent behavior fluid) : 소수의 비뉴턴 유체에 해당
⑷ 종류 2-1-1. 의소성 유체(슈도플라스틱, pseudo-plastic fluid) (예 : 시럽, 페인트 등)
① 정의 : 응력이 증가함에 따라 점성이 감소하는 유체. n < 1인 경우
② 전단 박화 유체(shear thinning fluid)라고도 함
③ 관류에서의 속도 분포 : 벽
○ 벽에서는 no slip 조건이 성립하므로 벽쪽으로 갈수록 속도 기울기가 증가함
○ 따라서 벽 근방에서는 점도의 감소효과가 두드러져서 벽 근방에서 유체의 속도기울기가 상대적으로 큼
④ 관류에서의 속도 분포 : 관의 중심
○ 관의 중심 부근에서는 속도기울기가 매우 작음
○ 따라서 점도가 상대적으로 커서 속도가 상대적으로 느리고 속도기울기도 작음
⑸ 종류 2-1-2. 팽창성 유체(딜레이턴트, dilatant fluid) (예 : 옥수수, 전분 등)
① 정의 : 딜레이턴트는 응력이 증가함에 따라 점성이 증가하는 유체. n > 1인 경우
○ 전단 농화 유체(shear thickening fluid)라고도 함
○ 즉, 평소에 액체지만 급격한 충격이 가해지면 고체가 됨
② 관류에서의 속도 분포 : 벽
○ 관벽에서는 점도가 두드러지게 증가함
○ 따라서 유체의 속도기울기가 작아짐
③ 관류에서의 속도 분포 : 관의 중심
○ 관의 중심 부근에서는 속도기울기가 매우 작음
○ 따라서 중심부로 갈수록 점도가 증가하므로 속도기울기가 커짐
④ 방탄조끼 등에 활용됨
⑹ 종류 2-1-3. 빙햄소성유체(Bingham plastic fluid) (예 : 치약, 마요네즈)
① 정의 : 유동이 시작되기 전까지 유한한 항복응력이 필요한 유체
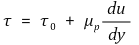
○ τ0 : 유동을 유발시키는 항복응력 (Pa)
② 이상소성 유체(ideal plastic fluid)라고도 함
③ 정성적 설명
○ 빙햄유체는 항복응력(yield stress) τ0가 꽤 큰 유체를 지칭
○ 관류에 대하여 τwall < τ0이면 빙햄유체가 정역학적 힘의 평형으로 유체가 흐를 수 없음
○ 관류에 대하여 τwall ≥ τ0이면 빙햄유체가 압력기울기 및 전단력 간 동역학적 힘의 평형으로 자연스럽게 유체가 흐름
○ (주석) 정역학적 힘의 평형은 정지 마찰력과 유사하고 동역학적 힘의 평형은 운동 마찰력과 유사함
⑺ 종류 2-2-1. 딕소트로픽 유체(thixotropic fluid)
① 정의 : 일정한 전단응력 하에서 시간에 따라서 겉보기 점도가 감소하는 유체
② 예 : 젤라틴(gelatin), 쇼트닝(shortening), 크림(cream), 페인트(paint) 등
⑻ 종류 2-2-2. 레오펙틱 유체(rheopectic fluid)
① 정의 : 일정한 전단응력 하에서 시간에 따라서 겉보기 점도가 증가하는 유체
② 예 : 고농축 녹말 용액
입력: 2016.12.01 22:28
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【유체역학】 4강. 미분형 방정식 (0) | 2016.12.08 |
|---|---|
| 【유체역학】 2강. 유체의 운동 방정식 (0) | 2016.12.01 |
| 【물질전달】 1강. 물질전달 및 복합전달 (2) | 2016.06.27 |
| 【열전달】 10강. 열교환기(Heat Exchanger) (0) | 2016.06.27 |
| 【열전달】 7강. 자연 대류계 (0) | 2016.06.27 |












최근댓글