1강. 물질전달(mass transfer) 및 복합전달(complex transfer)
추천글 : 【물질전달】 물질전달 목차
1. 플럭스 [본문]
2. 용액에서의 물질전달 (Fick의 법칙) [본문]
3. 기체에서의 물질전달 [본문]
4. 기타 이동현상 [본문]
5. 유체역학, 열역학과의 유사성 [본문]
6. 유체역학, 열역학과의 차이 [본문]
7. 응용 1. 기포, 표면장력, 부피감소율 [본문]
8. 응용 2. OMCVD법 [본문]
9. 응용 3. 혼합-침강기 [본문]
10. 응용 4. 생물반응공학 [본문]
11. 응용 5. 촉매의 기공을 통한 물질전달 [본문]
12. 응용 6. 수직 소금벽에서 물의 방향에 따른 소금의 용해속도 비교 [본문]
1. 플럭스(flux) [목차]
⑴ 플럭스 : 주어진 방향에 대하여 수직인 단위 면적을 통하여 단위 시간당 특정 물리량이 수송되는 비율
⑵ 몰 평균속도 v : A, B 이성분계에서 각 성분의 몰분율이 xA, xB이고 절대속도가 vA, vB일 때 v를 다음과 같이 정의

⑶ 몰 플럭스 N : A, B 이성분계에서 N을 다음과 같이 정의

⑷ 몰 평균속도에 대한 몰 확산 플럭스 J : A, B 이성분계에서 J를 다음과 같이 정의

2. Fick의 법칙 - 용액에서의 물질전달 [목차]
⑴ Fick의 법칙(Fick's law) : 1855년 최초로 제안됨
① 발상 : 약식으로 계산할 때 다음 공식을 사용할 수 있음
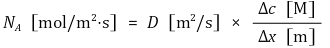
② 일정한 온도와 압력(21 ℃, 1 atm) 아래 정상상태이고 z방향으로만 확산이 일어난다고 가정하고, 주어진 계가 A와 B의 이성분계라 하면 물질전달식은 다음과 같다. 참고로 c는 A와 B의 몰농도 합이고 D는 확산계수(Diffusion Coefficient)이다.
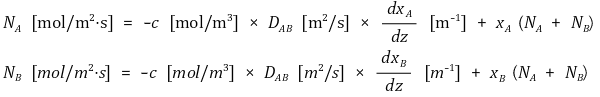
○ 첫 번째 항
○ A와 B 간의 농도차이에 의한 물질전달과 관련된 항
○ 몰분율 xA의 변화율에 영향을 주는 화학적 조성 차이(Composition Gradients, Activity Gradients)
○ 두 번째 항
○ 계 외부요인으로 인한 전체적인 움직임
○ 전체적인 움직임에 영향을 주는 열적·동적·전자기적·중력적 힘 등
○ 두 개의 물체가 서로 전기적 힘으로 상호작용(∽ 물질전달)하는 어떤 계가 중력이라는 Body Force의 영향(∽ 전체적인 움직임)을 받는 상황을 떠올리면 이해하기 쉬움
○ NB = 0인 경우가 많으며 이 경우 다음과 같이 식이 변형된다.
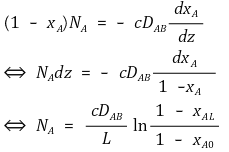
④ 아주 묽은 용액에서 용질의 확산계수는 Stokes-Einstein 식으로부터 다음과 같이 결정됨
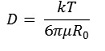
○ 단, k는 Boltzman 상수, T는 절대온도, μ는 용매점도, R0는 용질의 반지름
○ 가정 1. 용질의 확산의 driving force는 화학포텐셜의 기울기
○ 가정 2. 용질의 이동에 대한 저항은 Stokes 식으로 주어짐
○ 가정 1 보충 : 아주 묽은 용액이므로, 이상용액으로 가정할 수 있다. 이 경우 용질의 몰분율 x1에 대하여 화학포텐셜은 다음과 같이 주어진다.
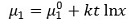
⑤ 작은 분자에 대한 확산계수 D의 실험적 결정
○ 1st. Fluo-EX labeling kit : 형광물질인 FITC와 conjugation
○ 2nd. Krypton-argon laser : FRAP 현상을 통해 분자들이 형광 빛을 발하도록 함
○ 3rd. CCD 카메라로 녹화한 뒤 Spatial Fourier Analysis Technique으로 위치좌표를 특정
○ 4th. Exponential Time Decay를 계산하여 확산계수 D를 결정
⑥ 출처
○ 이동현상의 응용과 해법, 이동현상 부문위원회(이현구), 한국화학공학회, 2002, 165 p.
○ R.B. Bird, W.E. Stewart, E.N. Lightfoot. (2002). Transport Phenomena 2nd edition. Wiley.
⑵ 일반적 표현
① 확산에 대한 구성방정식 : Fick의 법칙
② 확산도(diffusivity)가 D, 농도 C인 분자의 경우 몰플럭스 J는 다음과 같이 표현
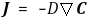
③ 대류에 의한 물질전달을 고려하면 물질보존식은 다음과 같음

④ 직각좌표계(x, y, z)에서 물질보존식
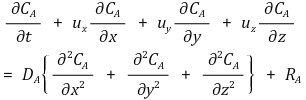
⑤ 원주좌표계(r, Φ, z)에서 물질보존식
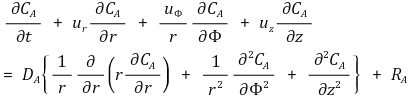
⑥ 구형좌표계(r, θ, Φ)에서 물질보존식
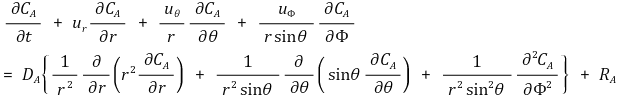
⑶ 물질확산(mass diffusion) : 열전도(heat conduction)와 유사
① ln(1-x)를 -x로 근사할 수 있음을 이용하면 다음과 같이 나타낼 수 있음
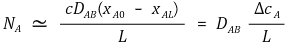
② 이는 열전도식이나 뉴턴의 전단응력식과 유사
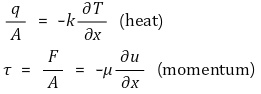
⑷ 확산에 의한 물질수송(mass transport by convection) : 열대류(heat convection)와 유사
① L ≪ 1 또는 L이 정형화 : DAB/L을 물질전달 계수(mass transfer coefficient) K라는 상수로 나타남
② 열전달 유사성 : 열확산식

3. 기체에서의 물질전달 [목차]
⑴ 개요
① A와 B의 확산계수 DAB에 대하여,
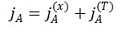
② 일반적으로 분자확산에 의한 물질전달은 액체에서보다 기체에서 더 빠르게 일어남
⑵ 농도차에 의한 Mass Flux
① 표현 1. A와 B의 확산계수 DAB에 대하여,
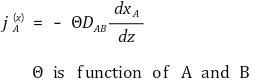
② 표현 2.
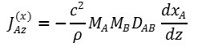
⑶ 온도차에 의한 Mass Flux : 압력차도 관여할 것임을 암시
① 표현 1. A와 B의 확산계수 DAB에 대하여,
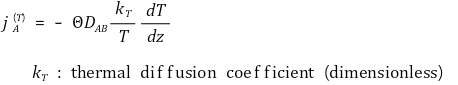
② 표현 2.
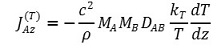
⑷ 응용 : 몰농도는 다르지만 몰분율이 같은 두 이상기체 계 사이에 물질전달이 일어나는가?
① 답. 일어나지 않는다. 앞서 c를 상수라고 가정했기 때문에 몰농도의 변화량으로 표현됐음을 유의하자. dxA/dz = 0이므로 물질전달이 일어나지 않는다.
② 참고. 물질전달은 화학퍼텐셜(Chemical Potential) 차이에 의해 일어난다. 이상기체의 경우 활성도(activity coefficient) γi가 1이므로 화학퍼텐셜은 다음과 같다.
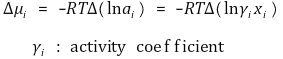
4. 기타 이동현상 [목차]
⑴ 커켄들 효과(Kirkendall effect)
① 이종성분 합금의 매끄러운 접합면을 고온으로 가열해 원자를 확산시켰을 때 얻어나는 접합경계면의 이동현상
5. 유체역학, 열역학과의 유사성 [목차]
⑴ 운동량 방정식(Momentum Equation)
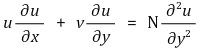
⑵ 열 방정식(Thermal Equation)
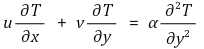
⑶ 물질 방정식(Mass Equation)
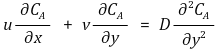
⑷ 속도와 온도의 비 : 즉, 동점도와 열확산도의 비
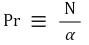
⑸ 속도와 농도의 비 : 즉, 동점도와 확산계수의 비
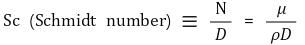
⑹ 온도와 농도의 비 : 즉, 열확산도와 확산계수의 비
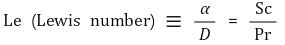
⑺ Nu 수 : 대류에 의한 열전달과 관련
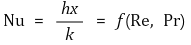
⑻ Sherwood 수 : 대류에 의한 물질전달과 관련
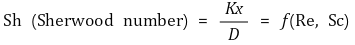
⑼ 열전달 상관식 : 누셀트 수
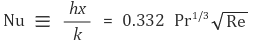
⑽ 물질전달 상관식
① 근사식 1
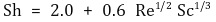
○ 위 식에서 2.0은 매우 희석된 농도에서 또는 등몰상호 확산조건 하에서 물질전달이 확산에 의해서만 진행될 때의 Sherwood 수를 의미
○ 실제로 확산에 의해서만 물질전달이 일어날 때의 물질전달식을 세우면 k = DAB / R임을 쉽게 보일 수 있음
② 근사식 2
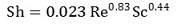
⑾ 기타 복합전달 상수
① Brinkman 수 : 점성소산(Viscous Dissipation)에 의한 열손실의 중요도를 결정한다.

6. 유체역학, 열역학과의 차이 [목차]
⑴ 열전도와 물질전달의 속도차이
① 문. 열전도는 기체에서보다 액체에서 더 빠르게 일어나지만, 분자확산에 의한 물질전달은 반대로 기체에서 더 빠르게 일어난다. 그 이유를 설명하시오.
② 답. 열은 분자의 진동에너지가 분자에서 분자로 전달됨에 의하여 이동되므로 분자 사이의 간격이 좁을수록 빠르게 전달될 수 있다. 그러나 확산은 분자 자체가 다른 분자들 사이로 이동하는 것이므로 분자 간격이 넓을수록 다른 분자와의 충돌 없이 빠르게 전달될 수 있다. 따라서 열전도도는 기체에서보다 액체에서, 분자확산속도는 액체에서보다 기체에서 더 크다.
⑵ 프란틀 수(Prandtl No.)와 슈미트 수(Schmidt No.)의 Dimension 차이
① 문. 기체에서는 열확산계수 α와 분자확산계수 D의 크기가 대략적으로 비슷하다. 즉, 상압 하에서 기체에서는 프란틀 수와 슈미트 수의 크기가 대략적으로 비슷하다. 액체의 경우 일반적으로 프란틀 수와 슈미트 수의 크기가 어떠한가?
② 답. 기체에서의 에너지전달, 물질전달은 주로 분자들의 Random Motion에 의한 실질적인 자리바꿈에 의해 일어나므로 열확산계수와 분자확산계수의 크기는 대략 비슷하다. 그러나 액체에서의 분자들의 운동은 기체에 비해 훨씬 제약을 받는다. 즉, 열전달은 분자들의 충돌, 진동, 자리바꿈 등 여러 가지 방법에 의해 전도가 일어나는 반면, 분자확산의 경우 실제적인 자리바꿈만이유일한 전달 방법이므로 훨씬 느리게 된다. 따라서 열확산계수에 비해 분자확산계수가 매우 작다.
⑶ 출처
① 이동현상의 응용과 해법, 이동현상 부문위원회(이현구), 한국화학공학회, 2002, 165 p.
② R.B. Bird, W.E. Stewart, E.N. Lightfoot. (2002). Transport Phenomena 2nd edition. Wiley.
7. 응용 1. 기포, 표면장력, 부피감소율 [목차]
⑴ 문. 크기가 서로 다른 두 기포가 액체 속에 있다. 기포 속의 기체는 액체에 잘 흡수된다. 어느 관찰자가 기포의 시간에 따른 부피변화를 측정한 결과 작은 기포의 부피는 빨리 감소하나, 큰 기포는 그 부피 감소율이 작은 기포에 비해 상대적으로 매우 느렸다. 그 이유를 설명하시오.
⑵ 답. Laplace 식에 의하면 외부압력이 같을 경우에 기포 내부압력은 같은 물질일 경우 기포 크기가 작을수록 크다.

기체의 경우 Henry의 법칙에 의해 일반적으로 액체에 대한 용해도는 압력이 클수록 크므로 작은 기포의 기체가 큰 기포 내의 기체보다 용해력이 커서 그 크기가 더 빨리 줄어든다.
⑶ 출처
① 이동현상의 응용과 해법, 이동현상 부문위원회(이현구), 한국화학공학회, 2002, 165 p.
② R.B. Bird, W.E. Stewart, E.N. Lightfoot. (2002). Transport Phenomena 2nd edition. Wiley.
8. 응용 2. OMCVD법 [목차]
⑴ 문. 갈륨비소(GaAs) 박막을 얻는 방법 중에 OMCVD(Organometallic Chemical Vapor Deposition)법이 있다. 대개 수소 Carrier 기체에, 반응물 아르신(AsH3, Arsine)과 TMG(Trimethyl Gallium)를 혼합한 혼합기체를 사용한다. 혼합기체로부터 반응물이 가열된 기판 위로 확산되어 기판 위에서 화학반응에 의하여 GaAs 박막이 형성된다. 균일한 두께의 박막을 얻기 위해서 보통 기판을 약 10° 정도의 경사로 기울이는 데 그 이유를 설명하시오.
⑵ 답. 평판인 경우에는 기체 흐름방향으로 진행하면서 경계층이 계속 자라게 되므로 물질전달 플럭스가 감소한다. 하지만 경사지게 기판을 배치하면 경계층은 자라지만 경계층 밖에서의 속도는 계속하여 증가하여(∵ 연속방정식) 경계층의 증가에 의한 물질전달 플럭스 감소효과와 속도의 증가에 의한 물질전달 플럭스 증가효과가 상쇄되어 물질전달 플럭스가 일정하게 유지될 수 있다. 즉, 성장하는 박막의 두께가 일정해질 수 있다.
⑶ 출처
① 이동현상의 응용과 해법, 이동현상 부문위원회(이현구), 한국화학공학회, 2002, 165 p.
② R.B. Bird, W.E. Stewart, E.N. Lightfoot. (2002). Transport Phenomena 2nd edition. Wiley.
9. 응용 3. 혼합-침강기(mixer-settler) [목차]
⑴ 문. 용매 추출공정에서 사용되는 혼합-침강기(mixer-settler)에 대하여 용매의 손실 및 장치의 크기를 최소화하기 위한 사항들을 열거하고, 혼합기의 성능을 높일 수 있는 방안을 제시하시오.
⑵ 용매의 손실 및 장치의 크기를 최소화하기 위한 방안 : 용매의 휘발성↓, 높은 분배계수 유지, 부유·침강속도 증가, 옹매를 분산상으로 유지, 침강기 표면적↓, 에멀션(emulsion)의 양↓, 슬러지(sludge)의 양↓
⑶ 혼합기의 성능을 높일 수 있는 방안 : 물질전달 또는 혼합이 잘 되도록 baffle 등을 사용하고 동력사용↓
⑷ 출처
① 이동현상의 응용과 해법, 이동현상 부문위원회(이현구), 한국화학공학회, 2002, 165 p.
② R.B. Bird, W.E. Stewart, E.N. Lightfoot. (2002). Transport Phenomena 2nd edition. Wiley.
10. 응용 4. 생물반응공학 [목차]
⑴ 문 1. 발효기에서 회분식으로 세포가 호기성으로 배양되고 있다. 어떤 시간 t0에서 배양액으로 분사되는 공기의 공급을 중단하는 것에 의해 탈산소화되었다. 그 후 공기가 일정 유속으로 배양액에 다시 공급되고 배양액의 산소 농도는 CLS로 유지되었다. 시간 t1과 t2 (t1 < t2)를 공기의 공급 중단과 다시 공급되는 사이의 시간이라고 할 때, 동역학적 방법으로 시간 t1과 t2 사이에서의 KLa를 아래에 제시한 기호(CLS, CL1, CL2)를 활용하여 유도하시오.
⑵ 답 1. 세포가 발효기 내 산소를 고갈시키지 않는다고 가정하자. (동역학적 방법이 적용되는 경우는 이런 가정이 필요하다.) 우선 정상상태 조건에서 미생물의 산소섭취속도 OUR(Oxygen Uptake Rate)을 계산할 수 있다.
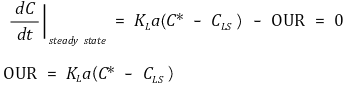
그런데 공기의 공급 중단과 다시 공급되는 사이의 시간에서 다음과 같은 식을 발견할 수 있다.
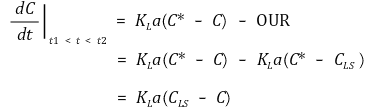
따라서 다음과 같다.
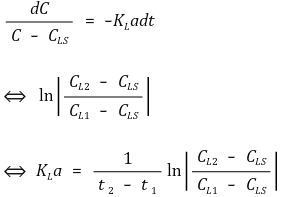
참고로 KLa는 물질전달계수 K를 지칭한다.
⑶ 문 2. 아래의 그래프를 이용하여 (1) 세포의 산소섭취속도(OUR)를 계산하고 (2) 세포 건조 중량이 2 g cell/L로 측정될 경우, 이 배양에서의 비호흡속도를 구하시오. (3) KLa를 정상상태 방법을 통하여 구하시오. 그래프에서 C* : 포화용존산소농도, CL : 시간 t에서의 산소농도, KLa : 시간당의 부피물질전달계수이다. (단, 곡선의 직선부분에 해당하는 공기 공급이 중단된 후 0.5분~3분 데이터를 직선으로 활용하시오.)
⑷ 답 2. 문제의 그래프는 기본적으로 동역학적인 방법으로 KLa를 구하는 그래프이다. 이를 정상상태 방법에 응용하면 산소공급이 중단된 시기에서 OUR 값을 구하고 정상상태가 되는 시점에서 dCL/dt = 0이 되는 것을 이용하여 최종적으로 KLa 값을 구할 수 있게 된다.
세포가 산소 공급을 중단하고 얼마 안 돼 반응기 내 산소를 거의 고갈시켰다고 가정하자. (정상상태 방법이 적용되는 경우는 이런 가정이 필요하다.) 따라서 반응기 내 산소와 맞닿은 수면의 용존 산소농도는 배양액의 산소농도와 같다. 즉, 산소전달속도 OTR(Oxygen Transfer Rate)을 다음과 같이 나타낼 수 있다.
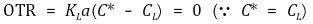
따라서 산소 공급이 중단될 때 시간에 따른 용존산소의 변화량은 아래와 같다.
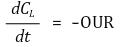
문제에서 주어진 대로 0.5분에서 3분까지의 데이터를 이용할 것이다.

세포 건조 중량(X)은 2 g/L이고 OUR은 비호흡속도 qO2와 세포의 중량(X)의 곱으로 표현되므로 앞에서 구한 OUR을 통해 비호흡속도를 구할 수 있다.
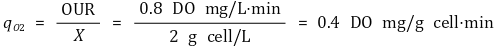
그래프에서 C* = 7.3 DO mg/L이고 20분 이후부터 CL = 2.3 DO mg/L로 유지되므로 시간에 따른 용존산소량은 0이 된다. 이를 KLa와 OUR 사이의 관계에서 표현하면 아래와 같이 계산된다.
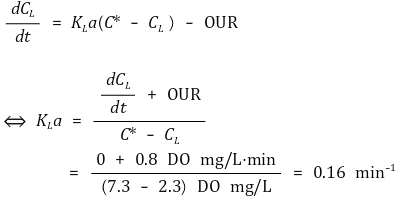
⑸ 출처 : 제18회 한국화학공학회 생명공학 경시대회(LG화학 후원) (생물반응공학 부문)
11. 응용 5. 촉매의 기공을 통한 물질전달 [목차]
⑴ 픽 확산(Fick diffusion) : 기공 크기가 확산기체의 Mean Free Path보다 훨씬 큰 경우에 일어나는 전달
⑵ 크누센 확산(Knudsen diffusion) : 기공 크기가 확산기체의 Mean Free Path와 같은 크기의 Order인 경우 일어나는 전달
⑶ 표면 확산(surface diffusion) : 상대적으로 많은 양의 분자가 흡착되어, 흡착된 분자가 기공변에서의 농도구배에 의해 표면을 따라 이동하는 현상
12. 응용 6. 수직 소금벽에서 물의 방향에 따른 소금의 용해속도 비교 [목차]
⑴ 발상 : 소금이 녹아 나오면 소금물은 물보다 밀도가 크므로 중력에 의하여 아래로 향하는 자연대류운동이 존재
⑵ 물이 중력방향인 경우 : 자연대류운동과 강제대류운동이 같은 방향이므로 용해속도가 비교적 빠름
⑶ 물이 중력반대방향인 경우 : 자연대류운동과 강제대류운동이 반대 방향이므로 용해속도가 비교적 느림
⑷ 출처
① 이동현상의 응용과 해법, 이동현상 부문위원회(이현구), 한국화학공학회, 2002, 165 p.
② R.B. Bird, W.E. Stewart, E.N. Lightfoot. (2002). Transport Phenomena 2nd edition. Wiley.
입력: 2016.06.09 00:41
수정: 2018.07.28 00:04
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【유체역학】 2강. 유체의 운동 방정식 (0) | 2016.12.01 |
|---|---|
| 【유체역학】 1강. 유체의 성질 (0) | 2016.12.01 |
| 【열전달】 10강. 열교환기(Heat Exchanger) (0) | 2016.06.27 |
| 【열전달】 7강. 자연 대류계 (0) | 2016.06.27 |
| 【열전달】 6강. 강제 대류계 (0) | 2016.06.27 |






최근댓글