2강. 유체의 운동 방정식
추천글 : 【물리학】 유체역학 목차
1. 연속방정식(continuity equation) [목차]

⑴ 정의 : 질량 보존의 법칙. 어느 단면에서나 통과한 유량은 동일
⑵ 수식화

⑶ 응용
① (참고) 다음과 같이 수식화할 수도 있음

② 비압축성 정상유동에 관한 연속 방정식

③ 압축성 정상유동에 관한 연속 방정식 : 밀도항이 추가됨
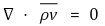
④ 압축성 비정상유동에 관한 연속 방정식 : 밀도항과 시간항이 추가됨
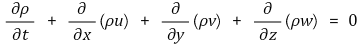
2. 오일러 방정식(Euler equation) [목차]

⑴ 정의 : 전단응력 없이 수직응력만 작용할 때 성립하는 법칙. 뉴턴법칙의 변형
⑵ 가정
① 유선, 즉 정상류
② 비압축성 흐름
③ 비점성 흐름
⑶ 수식화
① 검사체적에 작용하는 압력에 의한 힘
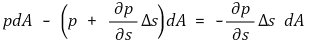
② 검사체적의 무게를 운동방향으로 분해한 성분
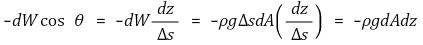
③ 운동방향으로의 가속도 성분
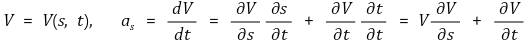
④ 뉴턴의 운동 제2법칙 적용
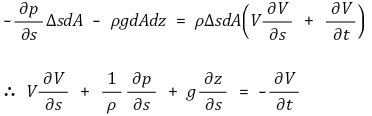
⑤ 정상상태 가정 적용
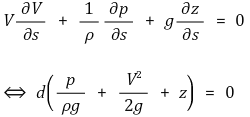
3. 베르누이 방정식(Bernoulli equation) [목차]
⑴ 정의 : 유선을 따라 오일러 방정식을 적분한 형태
⑵ 가정
① 유선, 즉 정상류
② 비압축성 흐름
③ 비점성 흐름
⑶ 수식화
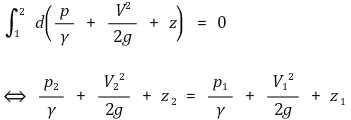
① p / γ : 압력수두(pressure head)
② V2 / 2g : 속도수두(velocity head)
③ z : 위치수두(potential head)
④ 수력구배선과 에너지선

⑷ (참고) 역학적 에너지 보존법칙을 통한 증명
⑸ (참고) 레이놀즈 수송 이론을 통한 증명
⑹ 응용 1. 날개가 없는 선풍기

① 1st. (가) : 공기는 날개가 없는 선풍기의 모터를 통해 속이 빈 고리 내부로 이동
② 2nd. (나) : 고리의 작은 틈으로 공기가 빠져 나감
③ 3rd. 틈이 좁아 틈으로 빠져 나간 공기의 속력이 빨라짐
④ 4th. 베르누이 방정식에 의해 공기의 압력이 작아짐
⑤ 5th. 대기압보다 압력이 낮아서 주변에 있던 공기가 앞서 공기 빠져 나간 방향으로 함께 들어가면서 연속적인 공기의 흐름을 만듦
⑥ 6th. A에서 B 방향으로 공기의 흐름이 형성됨
⑦ 날개 없는 선풍기는 처음 빨아들인 바람보다 15배나 많은 바람을 이동시킴
⑺ 응용 2. 마그누스 효과(Magnus effect)
① 정의 : 양쪽의 공기 흐름이 다를 경우 공이 똑바로 날아가지 못하고 압력이 낮은 쪽으로 커브를 돌게 되는 현상
② 공의 운동 방향과 회전 선속도가 같은 지점은 압력이 작고, 공의 운동 방향과 회전 선속도가 반대인 지점은 압력이 큼
⑻ 응용 3. 코안다 효과(Coanda effect)
① 정의 : 물체의 표면에 흐르는 유선(stream line)이 표면의 형상에 따라 흐르려고 하는 경향
② 원리 : 제트 상태의 유체 부근은 빠른 유속으로 압력이 낮고, 그 바깥은 압력이 높아 물체 표면을 따라 등압선이 형성
③ 응용 : 제트 안에 갇힌 물체는 제트가 움직이는 방향에 따라 같이 따라 움직이려고 함
4. 일-에너지 방정식 [목차]

⑴ 베르누이 방정식은 일-에너지 방정식의 특수한 형태
⑵ 수식화
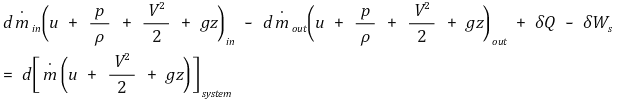
① u : 내부에너지 (J/kg)
② q : 투입열량 (J/kg)
③ ws : 축일 (J/kg)
5. 레이놀즈 수송 이론(Reynolds transport theorem) [목차]
⑴ 개요

Figure. 6. 레이놀즈 수송 이론 개요
① N : 종량적 성질(extensive property)
② η : N의 단위질량당 성질
③ 다음과 같은 성질이 발견
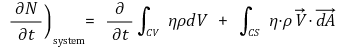
④ 증명
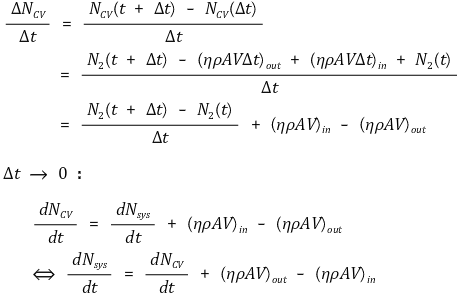
⑤ 기하학적으로 확장
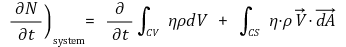
⑵ N = M, η = 1이라 두면,
어떤 system 내에서는 각 입자의 질량값이 보존되고, 입자의 존재도 보존되므로 질량이 보존된다.
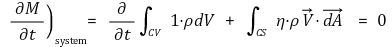
이는 모든 질량체적에 적용되는 식으로 종종 질량 평형이라고 한다.
⑶ 정상유동과정에 대한 질량 평형
① 정상유동과정에서 질량체적 내 밀도 변화는 항상 0임
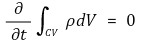
② 정상유동과정인 질량체적 내 밀도 변화는 항상 0이다. 따라서
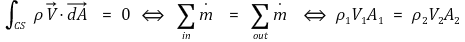
⑷ 정상비압축성 유동 : 밀도가 변하지 않는다. 즉, 압축되지 않는다.
입력: 2016.12.01 22:32
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【유체역학】 5강. 차원해석 (0) | 2016.12.08 |
|---|---|
| 【유체역학】 4강. 미분형 방정식 (0) | 2016.12.08 |
| 【유체역학】 1강. 유체의 성질 (0) | 2016.12.01 |
| 【물질전달】 1강. 물질전달 및 복합전달 (2) | 2016.06.27 |
| 【열전달】 10강. 열교환기(Heat Exchanger) (0) | 2016.06.27 |




최근댓글