5강. 차원해석(dimension analysis)
추천글 : 【물리학】 유체역학 목차
1. 모형(모델)과 프로토타입(실제 크기 모형) [목차]
⑴ 제품설계 과정 : 개념 설계 → 모형 설계 → 시뮬레이션 → 모형 시험 → 프로토타입 시험 → 시제품 → 제품
⑵ 모형을 만드는 이유 : 비용절감, 시간절감, 실험곤란(예 : 크기), 실험의 위험성
⑶ 모형의 유형 : 축소형과 확대형
⑷ 풍동(wind tunnel) : 고형의 물체 또는 주변에 대한 공기 움직임의 효과 연구를 위한 도구
Figure 1. 비행기 모형 시험을 위한 풍동
2. 버킹엄의 파이 정리(Buckingham PI theorem) [목차]
⑴ 차원(Dimension)
① 기본 차원(SI Base Units)은 총 7개이다.
② 점도(μ)의 단위는 kg/m·s이다. 점도의 차원은 ML-1T-1이다.
③ 동점도(ν or υ)의 단위는 m2/s이다. 동점도의 차원은 L2T-1이다.
④ 점도는 M을 포함하므로 물질의 특성과 관련된 반면, 동점도는 그렇지 않으므로 유동의 특성만 관련됨
⑵ 차원 분석의 본질
① n개의 독립변수 방정식을 표현하려면 n 차원 그래프를 그려야 한다.
② n개의 독립변수별로 10가지 조건을 시험한다면 10n(≫ 1)회의 실험이 필요
⑶ 버킹엄의 파이 정리
① 정리 : 어떤 n개의 독립변수가 m개의 기본차원으로 표시된다고 할 때, 다음 변환을 찾을 수 있다.
g(x1, x2, ..., xn) = 0 ⇔ G(∏1, ∏2, ..., ∏n-m) = 0
② 증명
○ 수식화
○ [a]를 변수 a의 차원이라고 정의
○ 기본차원 p1, p2, ..., pm에 대해 다음 행렬을 고려
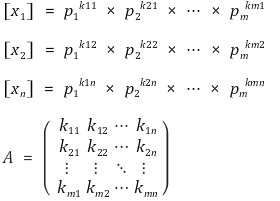
○ 위와 같은 행렬 A를 차원행렬(Dimensional Matrix)이라고 함
○ A에 의한 선형사상을 T : V → W라 하면, dim(V) = n임을 알 수 있음
○ rank-nullity theorem 적용
○ 다음과 같은 사실을 발견할 수 있음

○ 이때 y ∈ Y = im(A)는 x1을 v1승, ..., xn을 vn승한 것을 모두 곱한 것을 기본차원들로 나타낸 것
○ 기본차원의 개수가 m개이기 때문에 dim(im(A)) ≤ m임을 알 수 있음
○ 앞서 n개의 변수가 독립변수임을 알고 있으므로 dim(im(A)) < m일 이유가 없음 → dim(im(A)) = m임 (더 엄밀한 증명은 수학적 귀납법을 이용)
○ Rank-Nullity Theorem에 의해 kernel(A)의 차원은 n - m임을 알 수 있음
○ Av = 0, v ∈ V인 V의 차원이 n - m임
○ kernel과 무차원 변수
○ 행렬의 곱셈 결과가 0이라는 것은 기본차원으로 나타내었을 때 무차원이라는 것임
○ 따라서 주어진 x1, ..., xn을 조합해서 만든 무차원 변수는 n - m차원으로 제한됨
○ 다시 말하면 기껏해야 n - m개의 독립적인 무차원 변수를 찾을 수 있음
○ 그 이상 찾은 무차원 변수는 기존의 무차원 변수들의 적절한 곱으로 나타낼 수 있음
○ 그러므로 적절히 n - m개의 독립적인 무차원 변수를 찾은 뒤 실험을 통해 n - m차원의 그래프를 만들면, 이 그래프는 다른 실험 상황에서도 그대로 쓸 수 있음
○ 주의사항
○ 위 논리를 그대로 따라가면 이런 오류를 저지를 수 있음 : im 대신 kernel을 이용하려는 오류
○ 앞서 kernel의 기저벡터(무차원 변수)는 V의 원소들이었기 때문에 x1, ..., xn ∈ V의 정보를 얻을 수 있었음
○ 하지만 im(A)의 기저벡터(∈ W)는 p1, ..., pm이거나 그것의 선형조합인 정보로서 V와 동떨어진 정보를 가지므로 이들로 x1, ..., xn의 정보를 얻겠다는 것은 넌센스임
③ 응용 : 만일 G의 어떤 해 I가 있을 때, 또다른 변수의 조합 J가 I에서 사용된 n - m개의 무차원 변수의 값을 변화시키지 않을 때 J 또한 G의 해가 된다. 이는 모델 이론에서 가장 중요한 명제이다.
⑷ 무차원화
① 힌트 : 방정식의 모든 항은 동일한 차원을 가진다.
○ 즉, 한 계수가 무차원이면 다른 모든 계수들도 무차원이다.
② 예시
2차원 비압축성 정상유동의 Navier-Stokes Equation은 다음과 같다.
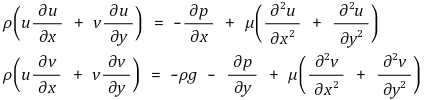
임의의 기준거리 L, 기준속도 V∞를 이용하여 각 변수를 무차원 변수화하자.

미분방정식의 각 항을 무차원 변수를 이용하여 표시하자.

미분방정식의 모든 항을 정리하면,
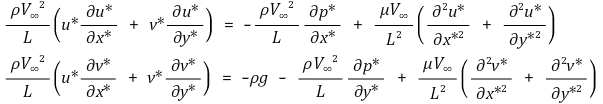
계수를 정리하면,

⑸ 무차원 변수 선택
① 1st. 반복변수(Repeating Variable) 선택
○ 반복변수의 조합은 모든 기본차원을 포함해야 하고 각각은 차원상 일차독립이어야 함
○ 반복변수는 다음 중 하나씩 선택한다; 유체의 성질(ρ, μ), 물체의 크기(L), 유동의 특성(V, ∂P/∂x)
○ 측정목적이 되는 변수 반복변수로 선택하지 않음
② 2nd. 각 비반복변수와 반복변수 조합을 새로 조합하여 무차원 변수를 만듦
○ 연립방정식을 푸는 과정이 요구됨
③ 차원 분석의 단점 : 특정 무차원 변수가 아니면 물리적 의미가 없는 식을 얻음
3. 중요한 무차원 변수들 [목차]
⑴ 레이놀즈 수 (Re, Reynolds number)
① 수식화

② 유체역학 전반에 걸쳐 중요하게 사용됨
⑵ 프루드 수 (Fr, Froude number)
① 수식화

○ 팁. √ gl의 차원이 속도와 같은 차원임을 유의
② 상황 1. 두 가지 혼합될 수 없는 유체가 접촉하는 흐름
③ 상황 2. 배와 같이 물과 분리되어야 할 때
⑶ 오일러 수 (Eu, Euler number)
① 수식화

② 압력 또는 압력차에 관한 상황에서 사용
⑷ 코시 수 (Ca, Cauchy number)
① 수식화

② 유체 압축이 중요한 상황에서 사용
⑸ 마하 수 (Ma, Mach number)
① 수식화

② 유체 압축이 중요한 상황에서 사용
⑹ 스트로우홀 수 (St, Strouhal number)
① 수식화

② 특정 주파수의 진동이 있는 비정상 유동에서 사용
⑺ 웨버 수 (We, Weber number)
① 수식화

② 표면장력이 중요한 흐름에서 역학적 상사성이 성립하기 위해 프루드 수를 같게 해야 함
⑻ 본드 수 (Bo, Bond number)
① 수식화

⑼ 갈릴레오 수 (Ga, Galileo number)
① 수식화
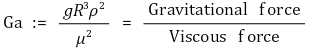
⑽ 모세관 수 (Ca, Capillary number)
① 수식화

⑾ 오네조르게 수 (Oh, Ohnesorge number)
① 수식화

4. 상사성 [목차]
⑴ 만일 모델로 실제 상황을 예측하고자 할 때, 모델과 프로토타입 간 성립해야 하는 동등조건
⑵ 상사성의 종류
① 기하적 상사성(geometric similarity) : 각도 일정, 방향(ex. 유속) 일정, 길이비 일정, 조도 일정
② 운동학적 상사성(kinematic similarity) : 속도(스케일 보정) 일정, 가속도(스케일 보정) 일정
③ 동역학적 상사성(dynamic similarity) : 압력 일정, 전단력 일정, 중력가속도 일정 등
④ 열역학적 상사성(thermodynamic similarity) : 온도 일정
⑤ 지배방정식(governing equation)에 관여하는 무차원 변수 값은 항상 같아야 함
⑶ 불완전 상사(incomplete similarity)
① 여러 무차원 변수의 값을 맞추는 게 현실적으로 어렵거나 논리적으로 불가능한 경우
② 해결책 1. 무차원 독립변수 중 어느 하나에 대하여 이론적 해석이나 별도의 실험자료를 이용하여 그 영향을 무시하거나 최악의 경우에는 영향을 미치는 정도를 무시하고 모형실험을 수행한다.
③ 해결책 2. 모형실험에서 변수의 범위가 넘는 경우에 모형실험식을 외삽하여 추정하기도 한다.
5. 차원해석 예제 [목차]
⑴ Planck 길이 : GR1776 14번, GR1775 12번
⑵ 표면 전하 밀도 : GR8677 63번
⑶ 켈빈 전하의 역수와 열역학 관계식 : GR8677 66번
입력: 2016.12.10 02:18
수정: 2023.12.20 14:18
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【유체역학】 7강. 외류 (0) | 2016.12.09 |
|---|---|
| 【유체역학】 6강. 내류 (0) | 2016.12.09 |
| 【유체역학】 4강. 미분형 방정식 (0) | 2016.12.08 |
| 【유체역학】 2강. 유체의 운동 방정식 (0) | 2016.12.01 |
| 【유체역학】 1강. 유체의 성질 (0) | 2016.12.01 |






최근댓글