6강. 내류(Internal Flow)
추천글 : 【물리학】 유체역학 목차
1. Reynolds 수에 따른 유동 특성 [본문]
2. 내류의 개념 [본문]
3. 마찰 수두의 개념 [본문]
4. 뉴턴 유체의 층류 유동 [본문]
5. 비뉴턴 유체의 층류 유동 [본문]
6. 뉴턴 유체의 난류 유동 [본문]
7. Three Types of Pipe-flow Problem [본문]
8. Flow in Non-circular Ducts [본문]
9. Minor Losses in Pipe Systems [본문]
10. Multiple Pipe Systems [본문]
11. Fluid Meters [본문]
1. Reynolds 수에 따른 유동 특성 [목차]
⑴ 점성유동의 3가지 영역
① 0 < Re < 1 : 고점성 층류 (Creeping Flow)
② 1 < Re < 102 : 층류, Reynolds 수의 영향이 큼
③ 102 < Re < 103 : 층류. 경계층 이론 적용 가능
④ 103 < Re < 104 : 난류로의 천이
○ 평판의 천이 구간 : 5 × 105 ~ 5 × 106
○ 관류의 천이 구간 : 2000 ~ 2300
⑤ 104 < Re < 106 : 난류. Reynolds 수의 영향이 보통
⑥ 106 < Re : 난류. Reynolds 수의 영향이 적음
Figure 1. 층류와 난류 : ⒜ 층류, ⒝ 천이구간, ⒞ 난류
⑵ 역사적 배경
① 층류와 난류의 차이 발견
② 압력차에 대한 근사식: Δp ∝ V (층류), Δp ∝ V1.75(난류)
Figure 2. 평균속력 대 압력차의 대략적인 그래프
2. 내류의 개념 [목차]
⑴ 내류(Internal Flow) : 유체가 벽에 의해 갇혀져 있다.
⑵ 입구 지역(Entrance Region) : Le로 표시
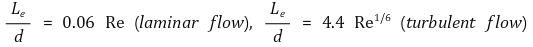
Figure 3. Entrance Region과 Fully Developed Flow Region의 묘사
3. 마찰수두의 개념 [목차]
⑴ 마찰수두(friction head) : 마찰에 의해 손실된 에너지를 길이의 차원으로 표시한 것. 베르누이 방정식에서 잘 드러남
⑵ 방정식 1. 베르누이 방정식

⑶ 방정식 2. 힘의 평형
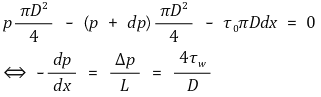
⑷ Darcy-Weisbach 식 (1850년) : 방정식 1과 방정식 2를 결합
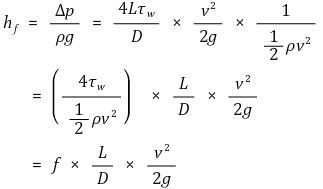
① f : 마찰계수
② L : 길이
③ D : 내경
④ v : 평균 유속
⑤ 팁. 손실수두 hf가 길이에 반비례하므로 D/L의 형태가 아니고 L/D의 형태가 돼야 함
⑥ 팁. 손실수두 hf는 속력이 클수록 크기 때문에 v2이 분모가 아니라 분자에 있음
⑸ 관 마찰계수(friction coefficient of pipe) f
① 정의 : Re, ε/d, 형상(duct shape)에 대한 무차원 변수
② 물리적 의미가 중요하기 때문에 무차원 그래프에서 자주 등장함
③ (평행) 일정한 관
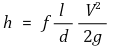
④ 돌연 축소관 (K = 0.5)
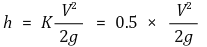
⑤ 돌연 확대관 (K = 1)
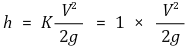
⑥ 임의의 관 : 축소계수 Cc에 대하여
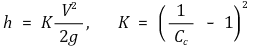
⑹ 표면마찰계수(skin friction coefficient) 또는 패닝 마찰계수(Fanning friction factor)
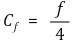
4. 뉴턴 유체의 층류 유동 [목차]
⑴ 가정 : 층류 완전 발달 관류(laminar fully developed pipe flow)
⑵ 방정식 1. 뉴턴의 제2법칙
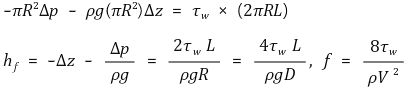
⑶ 방정식 2. 나비에-스톡스 방정식(Navier-Stokes equation)
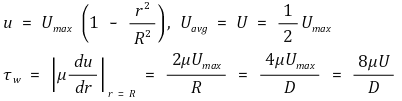
⑷ Darcy의 마찰 계수
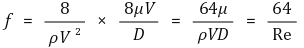
⑸ 마찰수두
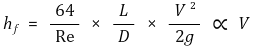
5. 비뉴턴 유체의 층류 유동 [목차]
⑴ (참고) 비뉴턴 유체의 겉보기 점도 : η로 표시
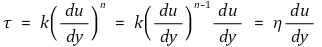
⑵ Metzner와 Reed는 비뉴턴 유체의 겉보기 점도를 다음과 같이 제시함
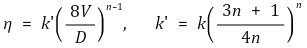
⑶ 일반화된 레이놀즈수(generalized Reynolds number)
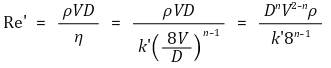
⑷ 비뉴턴 유체의 마찰계수
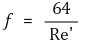
6. 뉴턴 유체의 난류 유동 [목차]
⑴ 난류유동
① 층류유동 : 경계조건과 함께 미분방정식의 해를 구하여, V와 p를 구할 수 있음
② 난류유동 : 시간에 따른 섭동 때문에 V와 p가 순간적으로 심하게 변화해서 정확한 해를 구할 수 없음
③ 난류유동의 경우 sliding friction이 있을 수 있음
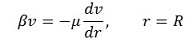
○ β : coefficient of sliding friction
⑵ 난류의 지배방정식(governing equation)
① 난류강도 (Intensity of Turbulent)
○ 새로운 통계적 개념
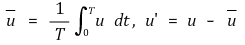

Figure 4. 임의의 함수를 평균함수와 오차함수로 분리하는 방법
○ High Turbulence : 터빈 또는 압축기의 내부, 5-20 %
○ Medium Turbulence : 파이프 또는 vet, 덕트, 1-5 %
○ Low Turbulence : 차 주변의 공기의 흐름, 자연대류, < 1 %
② Continuity Equation
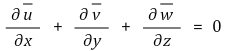
③ Navier-Stokes Equation
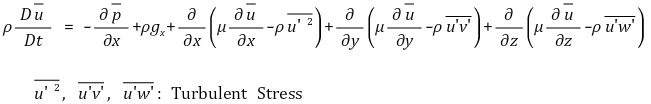
⑶ In Duct and Boundary Layer Flow
① 난류 전단력
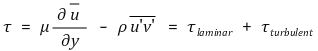
② 대수 중복층 법칙(logarithmic-overlap low)
○ (1) wall layer : Viscous shear stress is dominant
○ (2) outer layer : Turbulent shear stress is dominant
○ (3) overlap layer : Both types of shear stress are important
Figure 5. 벽 근처의 난에서 층류 전단력과 난류 전단력
③ Velocity in Wall Layer (Prandtle, 1930)
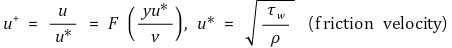
④ Velocity in Outer Layer (Kármán, 1933) : 유체의 점도와 무관, Velocity Defect Law
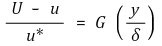
⑤ Velocity in Overlap Layer (Milikan, 1937)
○ Logarithmic-Overlap Low
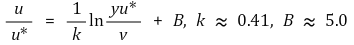
○ 전단 Reynold 수 (Shear Reynolds No)
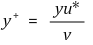
○ Wall Layer: 0 < y+ < 5
○ Overlap Layer: 5 < y+ < 30
○ Outer Layer: 30 < y+
○ 벽 층과 외층에서 약간의 오차가 있다.
Figure 6. 난류경계층 내에서의 속도분포 (Logarithmic-Overlap Low)
⑷ 매끈한 관의 마찰계수
① 자주 이용되는 식
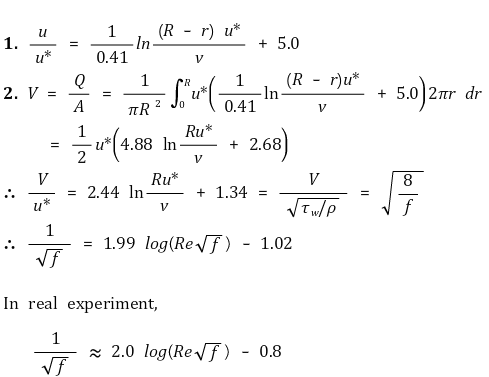
② Coulson-Richardson 식
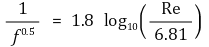
③ 기타
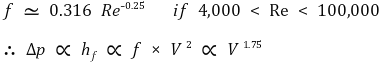
⑸ Rough Pipe 내 난류 (Wall Layer가 끝나는 지점)
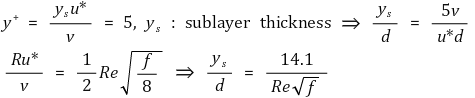
① 만일 조도(ε/d)가 sub-layer thickness보다 더 크면 sub-layer는 부서진다.
Figure 7. 난류인 관류에서의 조도의 영향:
⒜ log 함수적인 그래프는 우측아래로 편이, ⒝ sand-grain을 이용한 Nikuradse 실험
⑹ 거친 벽면의 3영역 (Nikuradse)
① εu*/ν < 5: Hydraulically smooth wall, No effect of roughness on friction, Depend on Re only
② 5 < εu*/ν < 70: Transitional roughness, Moderate Re effect
③ 70 < εu*/ν: Fully rough wall, 마찰은 Re와는 무관, 조도 ε만이 영향
⑺ 완전히 거친 벽면의 경우
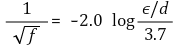
⑻ Moody Chart
① by Colebrook
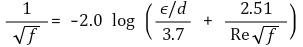
② Moody Chart: 정밀도 ± 15 %
③ by Haaland, 근사적으로
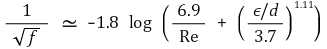
Figure 8. Moody Chart
7. Three Types of Pipe-flow Problem [목차]
⑴ 타입 Ⅰ
① Given : d, L, V or Q, μ, ρ, g
② Find : hf
⑵ 타입 Ⅱ : 시행착오법이 필요
① Given : d, L, hf, μ, ρ, g
② Find : V or Q
⑶ 타입 Ⅲ : 시행착오법이 필요
① Given : Q, L, hf, μ, ρ, g
② Find : d
8. Flow in Non-circular Ducts [목차]
⑴ 동수 반경 및 동수 직경
Rh = A / P (A: 면적, P: 둘레), Dh = 4Rh
⑵ 수정 마찰계수
f NCD = 8 τw, avg / (ρV 2)
⑶ 오차
① 층류: ± 40 %
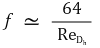
② 난류
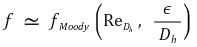
9. Minor Losses in Pipe Systems [목차]
⑴ 파이프의 유입, 유출구(Entrance Region Pressure Drop), 확대 및 축소, Bends, Elbows, Tees, Valves 등에서의 손실로, 실험에 의해 추정한다.
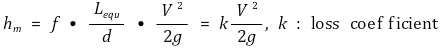
⑵ Open Valves, Elbows, Tees
Figure 9. ⒜ Gate Valve, ⒝ Glove Valve, ⒞ Angle Valve, ⒟ Swing-Check Valve, ⒠ Disk-Gate Valve
Table 1. Resistance Coefficient(K = hm / (V2 / 2g))
⑶ Partially Open Valves
Figure 10. Partially Open Valves에서의 평균 Loss Coefficient
⑷ 45°, 90°, 180° Bends
Figure 11. Red = 200,000일 때 45°, 90°, 180° Bends에서의 Resistance Coefficient
⑸ Sudden Expansion, SE
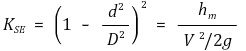
⑹ Sudden Contraction, SC
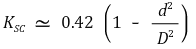
Figure 12. Sudden Expansion에 대한 그래프
⑺ Entrance Loss
Figure 13. Entrance Loss에 대한 그래프
⑻ Gradual Conical Expansion
Figure 14. Gradual Conical Expansion에 대한 그래프
⑼ Gradual Contraction
10. Multiple Pipe Systems[목차]

Figure 15. Multiple Pipe Systems. ⒜ Simple, ⒝ Series, ⒞ Parallel.
⑴ Series : 저항(마찰수두)의 직렬연결과 유사
⑵ Parallel : 저항(마찰수두)의 병렬연결과 유사
⑶ Reservoir Junction
Figure 16. Reservoir Junction의 예시
11. Fluid Meters[목차]
⑴ Local Velocity Measurements
① Float or Buoyant Particles
② Rotating Sensors
③ Pitot Static Tube : Yaw 각에 따라 2차 발생
④ Electromagnetic Current Meter : Conducting Fluid에 가해진 자장으로 인한 유동이 양극 전압 발생
⑤ Hot-wire Anemometer (열선 풍속계) : 열손실이 유속에 따라 변화
⑥ Laser-doppler Anemometer : 장점은 많으나 유체가 투명해야 하고 가격이 비싸다.
⑵ Volume-Flow Measurements
① Nutating Disc Meter
② Turbine Meter : 가장 많이 사용, 유체의 점도에 따라 Calibration이 필요
③ Vortex Flow-meter
④ Ultrasonic Flow-meter
⑤ Rotameter
⑥ Coriolis Mass Flow-meter
⑶ Head-loss Device to Measure the Volume-flow Rate
① Bernoulli Obstruction Theory : 파이프 내에 장애물 설치
입력: 2016.12.09 13:18
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【열전달】 열전달 목차 (0) | 2019.04.07 |
|---|---|
| 【유체역학】 7강. 외류 (0) | 2016.12.09 |
| 【유체역학】 5강. 차원해석 (0) | 2016.12.08 |
| 【유체역학】 4강. 미분형 방정식 (0) | 2016.12.08 |
| 【유체역학】 2강. 유체의 운동 방정식 (0) | 2016.12.01 |




















최근댓글