4강. 미분형 방정식
추천글 : 【물리학】 유체역학 목차
1. 지배방정식(governing equation) [목차]
⑴ 연속방정식(continuity equation)
속도벡터 u, 밀도 ρ인 유체의 연속방정식은 벡터기호를 써서 상징적으로 표현하면 다음과 같이 나타낼 수 있다.

⑵ 점성유체의 운동방정식
Cauchy의 운동방정식으로 알려져 있는 점성유체의 운동방정식은 Gibbs의 상징표현법으로 나타내면

과 같다. 여기서 P는 압력이며 ρg는 중력가속도와 같이 유체의 단위부피당 작용하는 물체힘(body force)을 나타낸다. 또한, 유체 변형과 관련된 τ는 편차응력텐서(deviatoric stress tensor) 또는 점성응력텐서이다.
우선 직각좌표계(x, y, z)에 대해서는 다음과 같다.
x 방향 성분 :

y 방향 성분 :

z 방향 성분 :

원주좌표계(r, Φ, z)에 대해서는 다음과 같다.
r 방향 성분 :
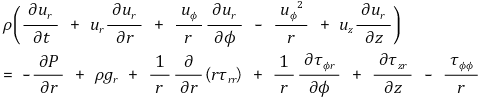
Φ 방향 성분 :
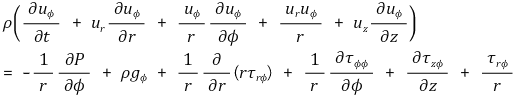
z 방향 성분 :
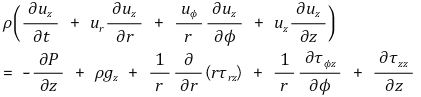
마지막으로 구형좌표계(r, θ, Φ)에 대해서는 다음과 같다.
r 방향 성분 :
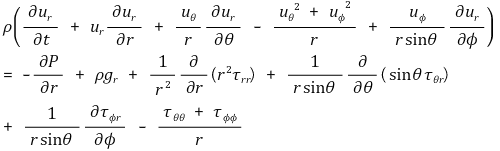
θ 방향 성분 :
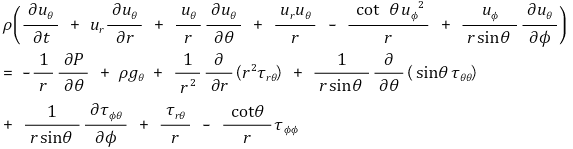
Φ 방향 성분 :
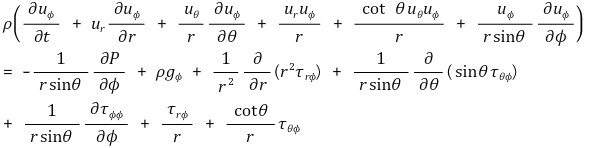
⑶ 변형률텐서(Rate of Strain Tensor)와 뉴턴유체의 구성방정식
유체의 변형률텐서 D는 속도벡터 u를 써서 다음과 같이 정의된다.
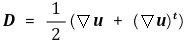
여기서 상첨자 t는 텐서의 전치(Transpose)를 나타낸다. 한편, 뉴턴유체의 구성방정식은 유체의 전단점도(Shear Viscosity) μ와 부피점도(Bulk Viscosity) κ를 써서

와 같이 표현된다. 여기서 I는 등방텐서(Isotropic Tensor)를 나타낸다.
직각좌표계(x, y, z)에서의 변형률텐서 및 구성방정식은 다음과 같다.
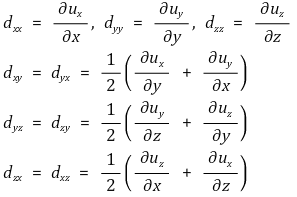
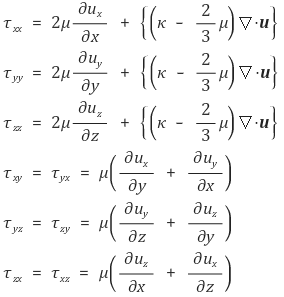
원주좌표계(r, Φ, z)에서의 변형률텐서 및 구성방정식은 다음과 같다.
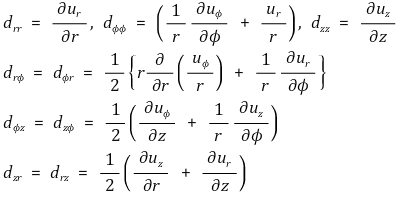
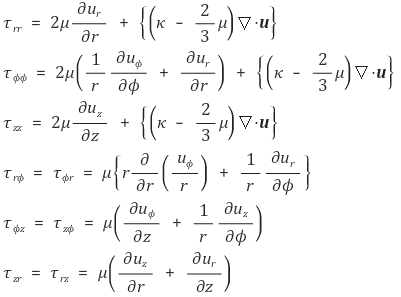
마지막으로 구형좌표계(r, θ, Φ)에서의 변형률텐서 및 구성방정식은 다음과 같다.
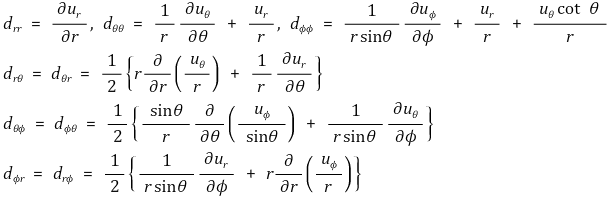
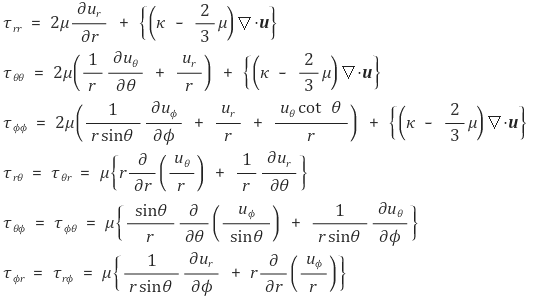
⑷ 비압축성 뉴턴유체의 운동방정식
흔히 나비에-스토크스(Navier-Stokes) 방정식으로 알려져 있는 뉴턴유체의 운동방정식은 Cauchy의 운동방정식에 뉴턴유체의 구성방정식을 대입하여 얻을 수 있다. 그 결과를 Gibbs의 상징표현법으로 나타내면 다음과 같다.
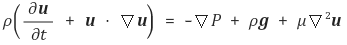
이를 직각좌표계(x, y, z)에 대해 나타내면 다음과 같다.
x 방향 성분 :
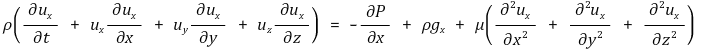
y 방향 성분 :
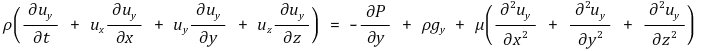
z 방향 성분 :
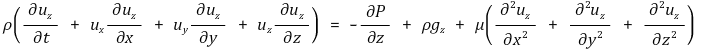
원주좌표계(r, θ, Φ), 구형좌표계(r, θ, Φ)에 대해서는 생략하겠다.
2. 지배방정식의 응용 [목차]
⑴ 경사면에서 Fully Developed된 층류의 연속방정식

Figure. 1. 경사면에서 Fully Developed된 층류
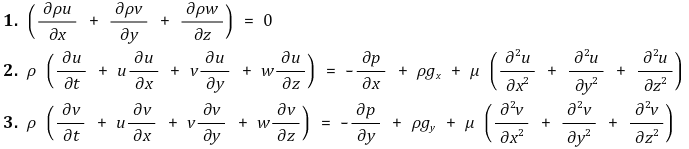
2D Flow이므로 z축 성분의 속도는 0이다.
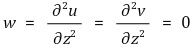
Fully Developed이므로 시간이나 x의 값에 따라 속도는 변하지 않는다.
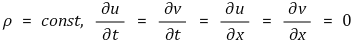
연속방정식에 의해 v = 0이다.
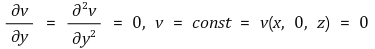
y축에 대한 Navier-Stokes Equation을 적용하면 x와 무관한 P의 식을 구할 수 있다.
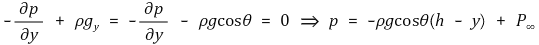
x축에 대한 Navier-Stokes Equation을 적용하면 u의 일반해를 구할 수 있다.
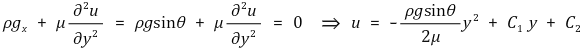
u(0) = 0, ∂u/∂y|(y=h) = 0이므로 u의 해를 정확히 구해낼 수 있다.
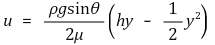
⑵ Couette 유동

Figure. 2. 두 개의 평행한 평판 사이의 점성층류유동 (z축 양끝부분에서 막혀 있음)
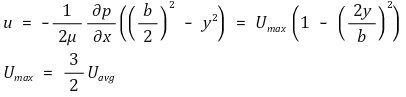
⑶ Hagen-Poiseuille 유동
① 수식화

Figure. 3. 원형관 안의 점성 층류유동
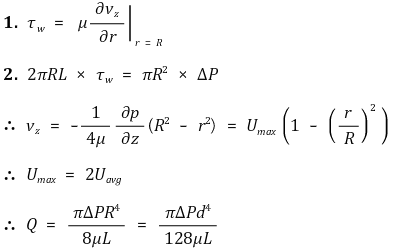
② 팁. Q ∝ ΔP × d4임을 그때그때 유도하는 게 편할 수도 있음
3. 연속함수 [목차]
⑴ 유선(streamline) : 속도 벡터에 접하는 방향을 가지는 연속적인 선
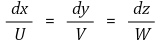
⑵ 유적선(pathline) : 한 유체 입자가 일정한 기간 내에 움직인 경로
⑶ 유맥선(streakline) : 공간 내의 한 점을 지나는 모든 유체 입자들의 순간 궤적 (예 : 한 순간의 담배 연기 궤적)
⑷ 속도 포텐셜(velocity potential)
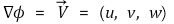
⑸ 유선함수(stream function)
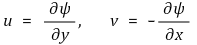
4. 점성소산의 이해 [목차]
⑴ 점성소산(점성소실, viscous dissipation) : 점성에 의한 운동에너지가 얼마나 열로 전환되는지에 대한 척도
⑵ 에너지 보존식과 점성소산
열전도에 대한 구성방정식은 Fourier 법칙이며, 이는 다음과 같이 표현된다.
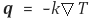
여기서 T는 온도, k는 열전도도, q는 열플럭스 벡터를 나타낸다. 열용량 Cp와 열전도도 및 밀도가 상수인 계에서 에너지 보존식은 다음과 같이 표현된다.
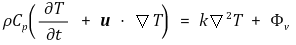
여기서 Φv가 점성소산으로서 유체의 점성마찰에 의해 열에너지로 변환되는 양이다.
직각좌표계(x, y, z)에서 점성소산은 다음과 같다.
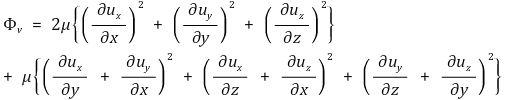
원주좌표계(r, Φ, z)에서 점성소산은 다음과 같다.
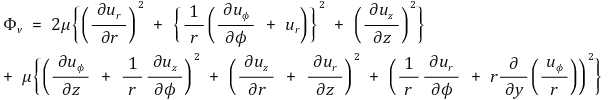
마지막으로 구형좌표계(r, θ, Φ)에서 점성소산은 다음과 같다.
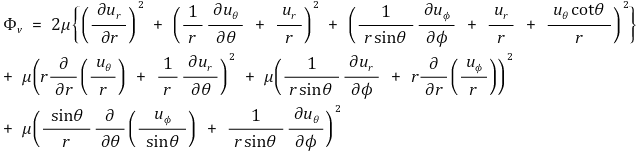
일반적으로 단순화된 문제를 접하게 될 것이며, 다음과 같은 공식을 자주 사용할 것이다.
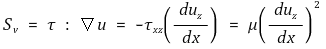
⑶ 직관

Figure. 4. 점성소성에 대한 문제 상황
x축으로 간격 H를 갖는 두 평판에 대해, 아랫판은 고정돼 있고, 윗판이 U(z축 방향)의 속도로 움직이면 두 평판 사이에서 일정한 전단응력이 생긴다. 두 평판 사이의 임의의 미소체적을 고려하면, 미소체적의 아랫변은 -u로 움직이고, 미소체적의 윗변은 u+du로 움직인다고 할 수 있다. τ가 윗변과 아랫변에 동일하게 작용하고 방향은 z축 방향이므로 미소체적은 τ(u+du) + τ(-u) = τdu만큼의 미소일이 미소체적에게 주어진다. 이는 미소체적의 x축 높이가 dx이므로 단위높이당 미소일은 τ du/dx임을 알 수 있다. 이러한 고찰은 크기만을 고려했음을 유의하자.
⑷ 점성소산은 유체역학과 열역학(특히 열전달) 개념이 필요한 복합전달 문제에서 곧잘 등장한다.
입력: 2016.12.08 20:28
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【유체역학】 6강. 내류 (0) | 2016.12.09 |
|---|---|
| 【유체역학】 5강. 차원해석 (0) | 2016.12.08 |
| 【유체역학】 2강. 유체의 운동 방정식 (0) | 2016.12.01 |
| 【유체역학】 1강. 유체의 성질 (0) | 2016.12.01 |
| 【물질전달】 1강. 물질전달 및 복합전달 (2) | 2016.06.27 |




최근댓글