추천글 : 【물리학】 유체역학 목차
1. 레이놀즈 수와 기하학적 효과 [목차]
⑴ 국소 Reynolds 수(local Reynolds number)
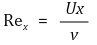
⑵ 속도경계층 : 팁. 일반기계기사에서 경계층 공식으로서 아래 공식을 사용하면 됨

Figure 1. Reynolds 수가 낮고 높은 경우에 평판을 지나는 유동의 비교
⒜ 층류, 낮은 Reynolds 수 유동, ⒝ 층류 및 난류, 높은 Reynolds 수 유동
Figure 2. 뭉특한 물체 뒤에서 점성과 비점성 영역 사이의 심한 간섭의 설명
⒜ 뭉특한 물체유동의 실제로 불가능한 이상적인 유동, ⒝ 실제 유동현상
2. 운동량 적분 추정량 [목차]
Figure 3. 평판 위의 속도경계층의 성장
⑴ 항력(drag force)
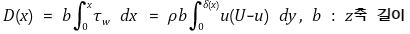
⑵ 평판(flat plate)에 대한 Kármán의 분석
① 운동량 두께(momentum thickness), θ
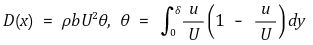
② 운동량 적분식(momentum integral relation)
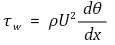
③ 속도 방정식
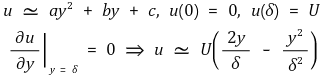
④ 층류 (Re < 3,000,000)
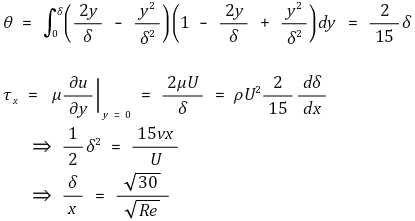
⑤ 표면마찰계수(skin friction coefficient), cf
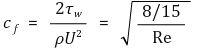
⑥ 배제두께(displacement thickness), δ*
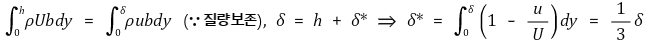
Figure 4. 경계층의 배제효과
⑸ 다른 평판 분석 : 평판을 일정한 속도 u로 잡아당겼을 때 유체의 속도 분포는 다음과 같이 나타낼 수도 있음
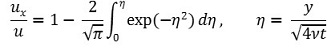
① u : 평판을 잡아당긴 속도
② μ : 점도
③ ρ : 밀도
④ ν : 동점도
3. 경계층 방정식 [목차]
⑴ 외부유동(external flow) 문제풀이 방법론
① numerical(digital-computer) solution
② experimentation
③ boundary-layer theory
⑵ derivation for 2D flow
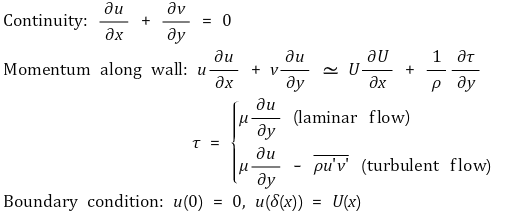
4. 평판의 경계층 해석 [목차]
Figure 5. 층류와 난류의 평판 속도분포의 비교
Figure 6. 매끈한 평판과 거친 평판의 층류와 난류경계층의 항력계수
이 도표는 평판에 대한 Moody 선도의 유사물
⑴ 층류
① Blasius 방정식 : f의 4차 미분 f'''', f의 2차 미분 f''에 대하여,
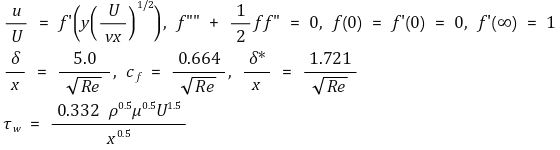
② 항력계수(drag coefficient)
○ 항력계수의 정의
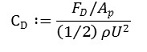
○ 항력(drag force)과의 연립
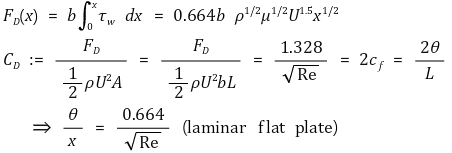
③ 형상계수(shape factor)
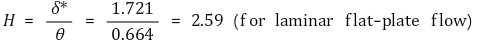
⑵ 천이구간 및 난류
① 벽을 다듬고(polishing) 자유 흐름(free stream)을 조용히 유지한 경우
Rex,tr = 3 × 106
② 일반적인 상업용 표면과 돌풍이 이는 자유 흐름(gusty free stream)
Rex,tr = 5 × 105
⑶ 난류
① 공식 1.
u / u* =(1 / 0.41)× ln(yu* / ν) + 5.0
u* = (τw / ρ)½
② 공식 2.
(2 / cf)½ = 2.44 ln(Reδ ×(cf / 2)½) + 5.0
③ 공식 3.
cf = 0.02 Reδ⅙
④ 공식 4.
(u / U)turb =(y / δ)⅐
⑤ 공식 5.
θ =(7 / 72)δ
⑥ x= 0, δ = 0으로 가정하면
Reδ = 0.19 Rex6 / 7 또는 (δ / x) = 0.16 / (Rex1.7)
⑦ 표면계수(skin-friction coefficient)
cf = 0.027 /(Rex⅐)
⑧ 공식 6.
τw, turb = 0.0135 μ⅐ρ(6 / 7)U(13 / 7)/x⅐
⑨ 항력계수(drag coefficient)
CD = 0.031 /(ReL⅐) =(7 / 6)cf (L)
⑩ 배제두께(displacement thickness)
δ* =(1 / 8)δ
⑪ 형상계수(shape factor)
H = δ* / θ = 1.3
⑫ 완전 거친 영역(fully rough regime)에서의 skin friction 및 drag
cf =(2.87 + 1.58 log (x / ε))2.5
CD =(1.89 + 1.62 log (L / ε))2.5
⑬ 천이(transition)가 시작되는 레이놀즈 수에 따른 천이 항력 곡선(transition drag curve)
CD = 0.031 /(ReL⅐) - 1440 /(ReL)(단, Retrans = 5 × 105일 때)
CD = 0.031 /(ReL⅐) - 8700 /(ReL)(단, Retrans = 3 × 106일 때)
5. 실제 외류 해석 [목차]
⑴ boundary layer thoery의 문제점
① 2차원 및 3차원 물체의 항력(drag)
○ blunt body
○ streamlined shape
② 부유하는 물체의 퍼포먼스
○ 익형(airfoil)과 항공기(aircraft)
○ 투사체(projectile) 및 핀 부착체(finned body)
○ 새와 곤충
⑵ 유체에 잠긴 물체에 작용하는 항력
Figure 7. 균일유동에 잠겨진 물체에 작용하는 힘과 모멘트의 정의
① 항력 : 유선(free stream line)을 따라 물체에 가해지는 힘
② 유선 방향에 대한 운동 분류
○ roll : 유선 방향에 대해 좌우로 흔들리는 운동
○ pitch : 유선 방향에 대해 위아래로 흔들리는 운동
○ yaw : 유선 방향이 바뀌는 운동
Figure 8. 유동이 두 대칭면에 평행하면 단지 항력성분만 있게 됨
③ 물체가 좌우대칭면을 갖고 있으면 roll, yaw 성분이 0이 됨
○ 이 경우 항력, 양력, pitch만 고려
○ 만약 유선이 수평면의 법선벡터에 수직하면 양력과 pitch 성분도 사라짐
④ 자유흐름속도(free-stream velocity)와 레이놀드 상수
Re = UL/ν
⑶ characteristic area
① 힘 계수(force coefficient)
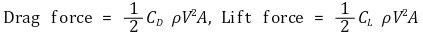
② 정면 면적(frontal area) : 유동 방향에서 본 물체의 면적으로, 구(sphere), 실린더(cylinder), 자동차(cars), 미사일(missiles), 투사체(projectiles), 어뢰(torpedoes)와 같이 두껍고 견고한 형상의 물체에 적합함
③ 평면 면적(planform area) : 위에서 본 물체의 면적으로, 날개(wings) 및 수중익(hydrofoils)과 같이 넓고 평평한 형상의 물체에 적합함
④ 습윤 면적(wetted area) : 주로 수상 선박(ships) 및 바지선(barges)에서 사용되는 면적
⑷ 마찰항력(Skin Friction Drag)과 압력항력(Form Drag, Pressure Drag) (ref)
① 수식화
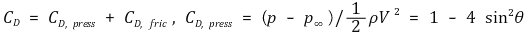
Figure 9. Rec = 106에서 유선형 2차원 실린더의 항력
⒜ 두께 비가 마찰항력의 백분율에 비치는 영향
⒝ 두 가지 다른 면적을 기준으로 하였을 때의 두께 비 대 총항력
② 박리현상과 후류
○ 박리 현상 (분리 현상) : 유동과정에서 발생한 역압력 구배에 의해 유체 입자가 이탈하는 현상
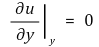
○ 후류(wake) : 항상 박리점 후방에 생김
Figure 10. 원형 실린더 주위의 유동
⒜ 층류박리, ⒝ 난류박리, ⒞ 이론적 및 실제적 표면압력분포
Figure 11. 원형실린더 주위의 유동의 묘사
⒜ 층류박리, ⒝난류박리
○ 출처 : 이동현상의 응용과 해법, 이동현상 부문위원회(이현구 등), 한국화학공학회, 2002, 49p.
○ 예전에는 골프공의 표면을 매끄럽게 제작하여 사용하였다. 그러나 사람들은 골프공이 낡아 표면이 거칠어졌을 때 더 멀리 날아가는 것을 경험적으로 알게 되었다. 지금은 골프공의 표면에 의도적으로 작은 홈(Dimple)을 300개 이상 만들어 사용하고 있다. 이와 같이 표면에 홈이 파진 골프공이 더 멀리 날아가는 이유를 서술하시오.
○ 매끈한 공의 경우, 공이 바른 속도로 나아갈 때 공의 중간쯤에서부터 경계층의 분리가 일어난다. 이때 공의 중간이후부터 공기의 속도가 급격하게 떨어짐과 동시에 공기의 흐름의 방향이 바뀌어 순환후류가 형성된다. 이 경우 공의 앞면에서는 높은 압력이, 뒷면에서는 낮은 압력이 걸려 큰 형태저항이 걸린다. 반면, 홈이 있는 공의 경우 공의 앞 표면에서 난류유동이 발생하여 경계층의 분리 및 순환후류가 훨씬 작아진다. 이렇게 되면 낮은 압력을 가지게 되는 공의 표면이 줄어들어 공의 저항이 감소한다.
Figure 12. 직경 8.5 in의 볼링공이 25 ft/s의 속도로 물 속에 잠길 때에 대한 층류와 난류박리의 중요한 차이
⒜ 매끈한 볼, 층류 경계층, ⒝ 같은 물 속의 낙하에서 앞부분이 모래로 거칠게 된 경우에 형성되는 난류경계층
(NAVAIR Weapons Division Historical Archives)
④ 포복흐름에서 총 항력 6πμUR 중 마찰항력이 2πμUR이고, 압력항력이 4πμUR이다. 반지름이 R인 기포는 마찰항력이 작용하지 않아 총 항력이 4πμUR인데 그 이유를 설명하겠다. 기표표면에서는 접선응력(τrθ)이 연속이어야 한다. 즉,
τrθ = τrθ*
여기서 τrθ, τrθ*는 각각 기포의 외부와 내부의 접선응력을 나타낸다. 그러나 접선응력이 점도에 비례하고 기포점도가 유체점도에 비해 무시할 수 있을 정도로 작으므로 접선응력은 0이 된다. 따라서, 기포의 경우 점성마찰항력은 0이 된다.
⑤ 다운워시(downwash)
○ 정의 : 비행기 날개에서 발생하는 공기 흐름이 아래 방향으로 휘어지는 현상
○ 베르누이 원리 : 비행기가 양력을 얻으려면 날개 위쪽의 공기는 상대적으로 빠르고 아래쪽 공기는 느려야 함
○ 날개 끝에서 공기가 회전하면서 와류(vortex)를 형성하고, 날개를 지나간 공기는 아래쪽으로 휘어지게 됨
○ 영향 : 유도항력 증가, 뒤따르는 비행기에 난기류 유발, 지면 효과 (다운워시가 지면과 반작용하면서 추가적인 양력이 발생)
⑸ 항력계수에 대한 직관
① 직관 : 특성길이가 lc인 물체가 비압축성 뉴턴액체에서 Re가 매우 크면 항력계수 CD는 Re에 관계없이 거의 일정
○ 출처 : 이동현상의 응용과 해법, 이동현상 부문위원회(이현구 등), 한국화학공학회, 2002, 26p.
② Re가 매우 클 때 : Re가 매우 크면서 층류라면 Figure. 11.과 같이 물체의 후면에서 경계층이 분리되고 순환와류가 발생한다. 이에 따라 물체에 작용하는 항력은 주로 압력으로부터 온다. 또한 압력은 베르누이 원리에 의해 (1/2)ρU2의 상수배가 된다. 해당 상수는 형상과 물리적 환경에 따라 물체에 영향을 미치는 유효비율과 관계된다. 그러므로 다음이 성립한다.

③ 물체가 유선형일 때 : 이때는 물체의 후면에서 경계층의 분리가 일어나지 않아서 순환와류가 발생하지 않아 점성응력이 항력을 지배한다. Re가 큰 층류에서 경계층 두께는 물체의 전체 표면에서 크기 차수가 O(lcRe-1/2)이다. 따라서 전단응력 τ는 경계층 내에서의 속도기울기에 비례하므로 크기차수는 τ = O(μURe1/2/lc)이고 항력 FD = O(μUlcRe1/2)이다. 그러므로 다음이 성립한다.
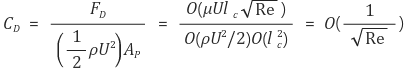
④ Re가 매우 작을 때 : 경계층 두께가 물체의 전체 표면에서 크기 차수가 O(lcRe-1/2)이 아님을 유의
⑹ 주요 도형의 항력계수
Figure 13. Re ≥ 104에서 2차원 물체의 항력계수
Figure 14. 낮은 Mach 수에서 매끈한 물체의 항력계수
⒜ 2차원 물체, ⒝ 3차원 물체.
문툭한 물체는 높은 Reynolds 수에서 Reynolds 수의 영향을 받지 않음에 주목
① 일부 대표적인 넓은 스팬(거의 2차원) 형상의 항력. 모든 형상은 매우 낮은 레이놀즈 수(Re ≤ 1.0, 서행 유동)에서 높은 항력 계수(CD)를 가지며, 높은 레이놀즈 수에서는 유선형 정도에 따라 항력 값이 달라진다.
⑺ 종말속도(terminal velocity)
① 정의 : 물체의 항력과 중력이 같아지는 순간의 낙하속도
② 방법 1. 갈릴레오 수(Galileo number), 레이놀즈 수(Reynolds number)를 이용
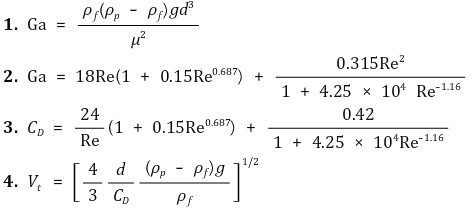
③ 방법 2. 구형물체가 아닌 경우 종말속도 방정식

⑻ 포복흐름(creeping flow)
① Re < 0.1 : Navier-Stokes 방정식에서의 가속도 성분은 무시됨
② 연속방정식과 Navier-Stokes 방정식 : 만일 Re가 매우 작다면,
∇·V = 0, ∇p ≃ μ∇2V
③ 구에서의 항력계수
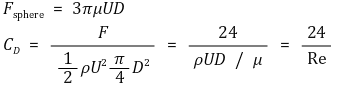
④ 유용한 공식 : 0 < Re < 6 × 103에서 구에 적용되는 항력계수는 다음과 같음
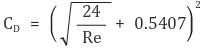
○ 이 식은 전국 대학생 화학공학 학력경시대회(이동현상)에서 유용하게 사용
⑤ 유용한 공식 : 0.1 ≤ Re ≤ 1000에서 구에 적용되는 항력계수는 다음과 같음
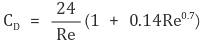
⑼ Biological Drag Reduction
Figure 15. 바람에 대한 생물학적 적응
⒜ 튜울립 나무의 잎들은 높은 풍속에서 원추형으로 감김
⒝ 검은 호두나무 잎사귀 등은 바람이 증가함에 따라 저항이 적은 다발 형태를 이룸
① 대부분의 이러한 연구는 강체 형상에 집중되어 있다. 그러나 자연에서는 다른 과정이 발생한다. 나무의 뿌리 시스템은 바람에 의해 발생하는 굽힘 모멘트에 저항할 수 있도록 여러 방식으로 진화해 왔다. 또한 나무의 줄기 단면은 굽힘에 강하지만 상대적으로 비틀리거나 재구성되기 쉬운 구조를 갖추고 있다.
⑽ 부유하는 물체에 작용하는 힘
① 이상적인 부유물(airfoil, hydrofoil, vane, etc)은 큰 양력과 작은 항력을 생성함
② 베르누이 원리 : 완만한 leading edge에서는 흐름을 가르지만, 날카로운 trailing edge에서는 비교적 나란한 흐름(wake)을 생성하며, 이로 인해 양력이 발생됨
Figure 16. 양력발생의 과도단계
⒜ 시작 : 뒷 정체점은 윗면에 위치함. 양력 없음
⒝ 날카로운 뒷전은 박리를 유발하고, 시동와류가 형성됨. 양력은 적음
⒞ 시동와류는 떨어져 나가고, 유선들은 후연으로부터 매끄럽게 유출됨. 약 80 %의 양력 발생
⒟ 시동와류는 멀리 떨어지고 뒷전 유동은 매구 매끄러움. 완전한 양력 발생
Figure 17. 양력날개의 부위별 명칭
CL,theory ≃ 2π sin(a + 2h/c)
③ 레이놀즈 수의 증가는 (기울기 변화 없이) 최대 양력을 증가시키고, 항력계수를 감소시킨다.
④ 분리플랩(split flap) : 날개에 부착되는 보조구조로서 airfoil을 비대칭적으로 만들어서 양각을 조절하여, 날개 전체의 운동 없이 양력을 효율적으로 이용할 수 있게 한다.
Figure 18. 무한수팬의 NACA0009 대칭형 익형의 양력과 항력
분리플랩의 전향각의 영향을 보여줌(α = -12°)
분리플랩이 CD를 100 ~ 300% 증가시킴에 유의
⑤ 양력을 발생시키는 비행체는 낮은 받음각에서 순항하며, 이때 양력은 항력보다 훨씬 크다. 유한한 날개폭은 가늘고 긴 형태(slenderness) 또는 종횡비(aspect ratio, AR)와 상관관계를 가질 수 있다.
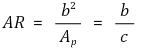
⑥ 유한 스팬 익형 이론에 따르면, 유효 받음각(effective angle of attack)은 다음과 같은 양만큼 증가한다.
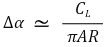
Figure 19. 표준형(0009)과 층류운동형(63-009)의 NACA 익형의 양력-항력 극좌표 도시
Figure 20. 유한 종횡비가 익형의 양력과 항력에 미치는 영향
⒜ 유효각 증가, ⒝ 유도항력 증가
⑦ 유한 스팬에서의 양력은 다음과 같이 표현됨
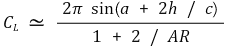
⑧ 이에 따른 항력 증가는 다음과 같음
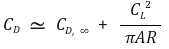
⑨ 최대 양력 계수가 존재한다는 것은 양력이 기체의 무게를 지탱하는 경우 최소 속도, 즉 실속 속도(stall speed)가 존재함을 의미
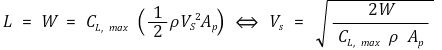
Figure. 21. 고양력장치에 따른 성능
A = NACA 0009; B = NACA 63-009; C = Kline-Fogleman형; D~I는 상기 표기
⒜ 고양력장치의 형태, ⒝ 여러 가지 장치에 대한 양력계수
⑩ (참고) Kwtta Kaukowski의 정리
○ V : 평행흐름. Γ : 물체 둘레의 순환. L : 양력. ρ : 유체의 밀도
○ 원통표면상의 한 점 P
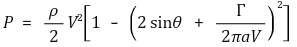
○ 양력 L에 대한 공식
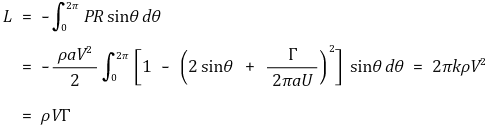
입력: 2016.12.09 13:18
수정: 2025.02.22 00:45
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【물질전달】 2강. 함수율 (0) | 2019.09.23 |
|---|---|
| 【열전달】 열전달 목차 (0) | 2019.04.07 |
| 【유체역학】 6강. 내류 (0) | 2016.12.09 |
| 【유체역학】 5강. 차원해석 (0) | 2016.12.08 |
| 【유체역학】 4강. 미분형 방정식 (0) | 2016.12.08 |

























최근댓글