10강. 액체와 고체
1. 액체, 고체의 정의 [목차]
⑴ 액체의 정의는 기체나 고체보다 모호함
① 기체 : 분자간 인력이 거의 없음
② 고체 : 공간 상에 고정돼 있음
③ 액체 : 유동적이지만 서로 벗어나지 못함, 매니스커스가 액체를 정의할 때도 쓰임
⑵ 배열(ordering)에 따른 정의
① 기체 : ordering이 없음
② 고체 : long-range ordering
③ 액체 : short-range ordering
⑶ 진동 진폭에 따른 정의
① 기체
② 고체 : 결정구조에서 입자와 입자 간의 거리에 반 미만으로 진동하는 경우
③ 액체 : 결정구조에서 입자와 입자 간 거리의 반 이상으로 진동하는 경우
⑷ 액정(liquid crystal) : 액체이지만 고체처럼 ordering이 유지되는 경우
① nematic phase : 같은 방향, 어긋남
② smectic phase : 같은 방향, 일정 간격
③ cholesteric phase : 다음 layer가 기존 layer에 일정한 각도로 기울어져 있을 때
2. 액체의 성질 [목차]
⑴ 표면장력
⑵ 점성도
⑶ 증기압
① 증기압과 끓는점
○ 증기압 : 액체의 증발과 응축이 평형에 도달했을 때 증기가 갖는 압력
○ 끓는점 : 액체의 증기압이 외부 압력과 같아질 때의 압력
○ 정상 끓는점 Tb : 1기압에서의 끓는점
② 증기상평형(예 : 물)
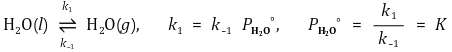
③ 온도와 르샤틀리에 법칙
○ 증기상(김, steam)이 기체상(수증기, vapor)이 되는 반응은 흡열반응, 즉 ΔH < 0
○ 온도 증가 ⇒ 르샤틀리에 법칙에 의해 온도를 줄이려는 흡열반응으로 평형 이동 ⇒ K 증가 ⇒ 증기압 증가
④ 클라우지우스-클라페이론(Clausius-Clapeyron)
○ 수식화 : 절대온도 T에 대하여
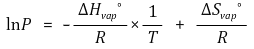
○ 유도
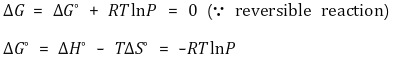
○ 서로 다른 온도에서의 증기압
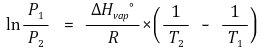
○ 증발 엔탈피와 증발 엔트로피 계산
○ 가정 : 온도에 따라 증발 엔탈피와 증발 엔트로피가 변하지 않는다고 가정
○ 증발 엔탈피 계산 : ln P - 1/T 곡선에서 기울기를 구한 뒤 (-R)을 곱함
Figure. 1. 증발 엔탈피 계산
○ 증발 엔트로피 계산
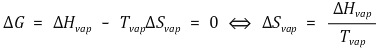
⑤ Antoine 식 : 증기압을 구하는 실험적인 식
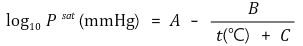
⑷ 음펨바 현상
① 정의 : 어는점 아래로 온도가 내려가도 응고하지 않는 현상, 즉 과냉각현상 (예 : 물)
② 원리 : 물의 육각구조 형성시간이 오래 걸려 어는점 아래에서 얼지 않는 현상
3. 고체의 성질 [목차]
⑴ 고체의 종류
① 결정성 고체와 비결정성 고체로 구분
② 결정성 고체는 분자결정
③ 종류 1. 금속결정(metallic solid) : 금속결합(전자의 바다). 전기전도도 있음 (예 : Na)
④ 종류 2. 이온결정(ionic solid) : 이온결합. 액체상태만 전기전도도 있음 (예 : NaCl)
⑤ 종류 3. 원자결정(network solid) : 공유결합. 전기전도도 없음
○ 아보가드로수를 정의한 수단
○ 반례 : 탄소 결정은 고체 상태에서 전기전도성을 가짐
⑥ 종류 4. 분자결정(molecular solid) : 분자간 힘. 전기전도도 없음
⑵ 금속 결정의 구조
① 개요
○ nearest neighbor : 어떤 원자 혹은 이온을 중심으로 가장 가까운 거리에 있는 원자
○ 일반적인 배위수 : 특정 원자와 가장 가까운 원자의 수
○ 음이온의 배위수 : 특정 음이온과 가장 가까운 양이온의 수
○ 양이온의 배위수 : 특정 양이온과 가장 가까운 음이온의 수
○ 금속 결정의 단위세포는 총 14 종류가 있음
Figure. 3. 육방밀집구조
② 단순입방구조(simple-cubic, primitive-cubic)
○ 형태 : 정육면체의 8개의 꼭짓점에 원자가 있음
○ 단위세포 내 입자수 : 꼭짓점 원자는 1/8반구임
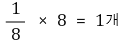
○ 배위수 : 세 개의 축으로 각각 2개, 총 6개
○ 반지름 관계 : 한 변의 길이 a에 대해
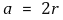
○ 공간점유율 : 점유율이 낮아 자연계에서 드묾

○ 밀도

○ 쌓는 방법 : 가장 똑바로 배열하면 됨
③ 체심입방구조(BCC, body-centered-cubic)
○ Cr, W, Mo, V, Li, Na, Ta, K, α-Fe, δ-Fe 등
○ 형태 : 정육면체의 8개의 꼭짓점에 원자가 있고, 정육면체의 중심에 1개의 원자가 있음
○ 물리적 성질 : 융점이 높고 강도가 큼
○ 단위세포 내 입자수 : 꼭짓점 원자는 1/8반구이고, 중심원자는 하나의 구임
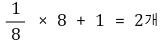
○ 배위수 : 중심원자를 기준으로 생각하면 편함. 8개
○ 반지름 관계 : 한 변의 길이 a에 대해 3차원 대각선을 생각하면
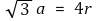
○ 공간점유율
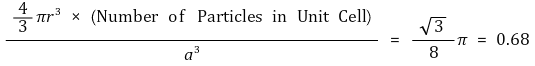
○ 밀도
○ 쌓는 방법 : 각 층은 똑바로 배열하고, 윗층과 아랫층은 어긋나게 쌓으면 됨
④ 면심입방구조(입방조밀쌓임, FCC, face-centered-cubic, cubic close-packed)
○ Al, Ag, Au, Cu, Ni, Pb, Ca, Co, γ-Fe 등
○ 형태 : 정육면체의 8개의 꼭짓점에 원자가 있고, 정육면체의 6개 면의 중심에 원자가 있음
○ 물리적 성질 : 전기전도율이 크고 가공성이 우수함
○ 단위세포 내 입자수 : 꼭짓점 원자는 1/8반구이고, 면 원자는 1/2반구임
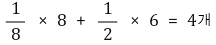
○ 배위수 : 면 원자를 기준으로 하면 해당 면에 4개, 해당 면 앞에 4개, 해당 면 뒤에 4개, 총 12개임을 알 수 있음
○ 반지름 관계 : 한 변의 길이 a에 대해 2차원 대각선을 생각하면
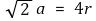
○ 공간점유율 : 가장 조밀하게 쌓음
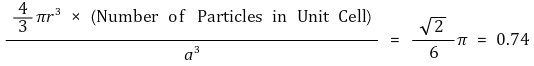
○ 밀도
○ 쌓는 방법 : 임의의 열은 주위의 모든 열과 어긋나도록 쌓으면 됨
⑤ 육방밀집구조(육방조밀쌓임, HCP, hexagonal closed packed)
○ Mg, Zn, Cd, Ti, Be, Zr, Ce 등
○ 형태 : 6개 - 3개 - 6개의 단위세포가 벌집처럼 붙는 구조
○ 물리적 성질 : 전기전도성, 접착성, 가공성이 불량함
○ 단위세포 내 입자수 : 꼭짓점 원자는 1/6반구이고, 육각형 면 원자는 1/2반구임, 또 내부 3개는 단일구임
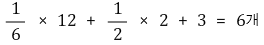
○ 배위수 : 12개. Figure. 3.에서 위·아랫면의 중앙 원자를 상기하면 쉽게 이해할 수 있음
○ 반지름 관계 : 한 변의 길이 a에 대해
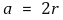
○ 공간점유율 : 면심입방구조처럼 가장 조밀하게 쌓음
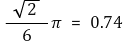
○ 밀도
⑥ 철의 결정구조
| α 형 | γ 형 | δ 형 | |
| 온도 (℃) | 906 ℃ 이하 | 906 ~ 1401 ℃ | 1401 ℃ 이상 |
| 밀도 (g / ㎤) | 7.9 | 8.6 | 약 7.9 |
| 결정구조 | 단순입방 | 면심입방 | 체심입방 |
Table. 1. 철의 구조
⑶ 이온결정의 구조
① 이온 결정의 예시
② 이온결합의 결합에너지
○ 단일 쌍극자의 쿨롱 퍼텐셜
Figure. 5. 단일 쌍극자의 쿨롱 퍼텐셜
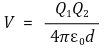
○ 1차원 결정의 쿨롱 퍼텐셜 : 무한한 1차원 결정의 중심 원자의 쿨롱 퍼텐셜에 아보가드로 수를 곱함
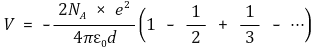
○ NaCl 결정의 쿨롱 퍼텐셜 : 무한한 3차원 결정의 중심 원자의 쿨롱 퍼텐셜에 아보가드로 수를 곱함
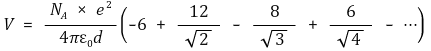
○ CsCl 결정의 쿨롱 퍼텐셜 : 무한한 3차원 결정의 중심 원자의 쿨롱 퍼텐셜에 아보가드로 수를 곱함
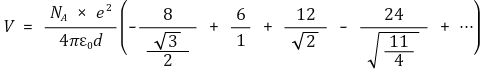
○ 격자에너지 : 쿨롱 퍼텐셜의 절댓값을 의미함. 격자에너지가 작을수록 용해도가 큼
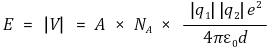
○ 이온결합의 결합에너지 = - 금속 이온화에너지 + 비금속 전자친화도 + 격자에너지
○ 금속 이온화에너지 : E(Na+(g)) - E(Na(g))
○ 비금속 전자친화도 : E(Cl (g)) - E(Cl- (g))
○ 격자에너지(lattice energy) : E(Na+ (g)) + E(Cl- (g)) - E(NaCl(s))
○ 이온결합의 결합에너지 : E(Na(g)) + E(Cl(g)) - E(NaCl(s))
③ 면심입방구조의 구멍
○ 면심입방구조는 두 종류의 구멍(hole)이 존재
○ 정사면체 틈새 : 면심입방구조에서 사면체 틈새는 각 꼭짓점을 중심으로 8개 존재 (구체적인 좌표를 구하는 과정)
○ 정팔면체 틈새 : 면심입방구조에서 팔면체 틈새는 4개 존재, 다음과 같이 확인
Figure. 6. 팔면체 틈새 팁
○ 정사면체 틈새가 정팔면체 틈새보다 작음
⑷ 원자결정의 구조
① 다이아몬드의 구조
○ 다이아몬드의 전체 구조
○ 다이아몬드의 단위 세포의 구조 : 단위 세포에는 8개의 원자가 포함돼 있음
○ 공간점유율
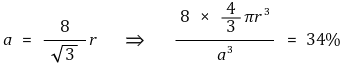
⑸ 실제 결정의 구조
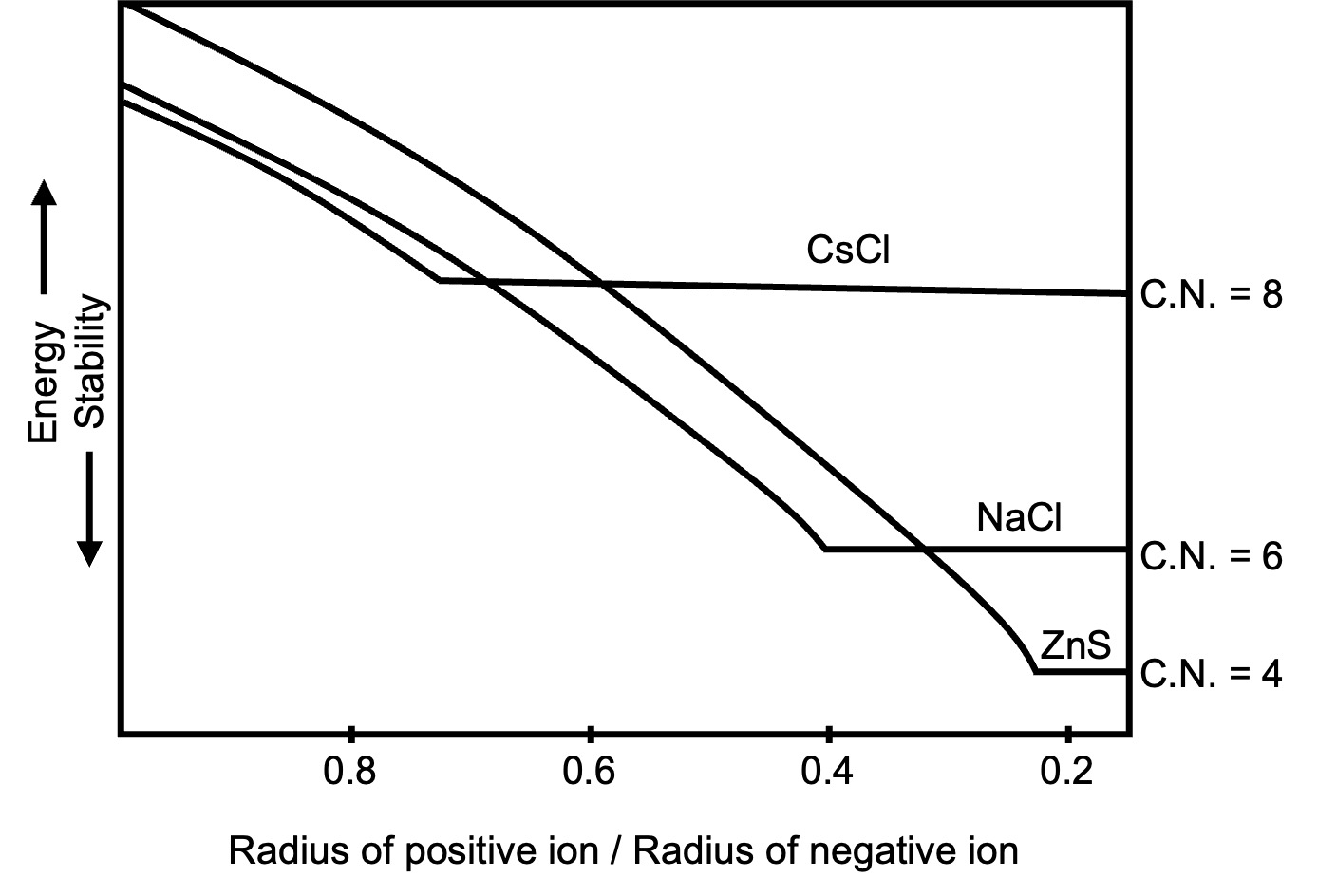
Figure. 9. 실제 결정의 구조
① 일반적으로 잘 알려진 결정구조는 가장 대칭적인 구조이고, 실제 결정구조는 이 대칭성이 깨짐
② 이온 결정에서 양이온-음이온 간 인력이 강해지면 격자를 이루는 단위 셀의 각 면이 오목해지는 경향이 생김
③ 이온 결정에서 양이온-양이온 혹은 음이온-음이온 간 척력이 강해지면 격자를 이루는 단위 셀의 각 면이 볼록해지는 경향이 생김
④ 척력이 충분히 존재하면 격자구조가 바깥으로 팽창하는 힘이 생겨서 배위수가 일정하게 유지되는 격자를 형성하려는 경향이 생김
⑤ 척력이 충분히 존재하지 않으면 결정 구조가 깨지고 배위수가 불규칙해지며 에너지 수준이 높아짐
입력: 2018.12.30 22:29
수정: 2024.08.10 14:47
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 13강. 열역학 (42) | 2018.12.27 |
|---|---|
| 【화학】 11강. 용액 (0) | 2018.12.27 |
| 【화학】 12강. 혼합물의 분리 (0) | 2018.12.27 |
| 【화학】 9강. 기체 (2) | 2018.12.27 |
| 【화학】 8강. 물질의 상태 (0) | 2018.12.27 |












최근댓글