11강. 용액(solution)
추천글 : 【화학】 화학 목차
1. (참고) 물질의 분류 [목차]
⑴ 순물질 : 홑원소 물질과 화합물로 구분
⑵ 혼합물 : 균일 혼합물과 불균일 혼합물로 구분
⑶ 홑원소 물질
① 한 가지의 원소로만 이루어진 물질
② 예 : 구리(Cu), 질소(N2), 철(Fe), 다이아몬드(C), 알루미늄(Al)
⑷ 화합물
① 두 가지 이상의 다른 원소들이 일정 비율로 구성된 물질
② 예 : 이산화탄소(CO2), 황산구리(CuSO4), 물(H2O)
⑸ 균일 혼합물(용액)
① 두 가지 이상의 순물질이 균일하게 섞여서 모든 부분의 조성이 같은 혼합물
② 예 : 공기, 설탕물
⑹ 불균일 혼합물
① 두 가지 이상의 순물질이 불균일하게 섞여서 취하는 부분에 따라 조성이 다른 혼합물
② 예 : 흙탕물, 우유
2. 개요 [목차]
⑴ 용액의 형성
① 용매(solvent) : 녹이는 물질
○ 예 : 소금물에서 물
○ 예 : 에탄올 수용액에서 더 많은 양을 차지하는 것
② 용질(solute) : 녹는 물질
○ 예 : 소금물에서 소금
○ 예 : 에탄올 수용액에서 더 적은 양을 차지하는 것
③ 용해(solvation) : 용질이 용매에 녹는 현상
○ 용액이 형성될 때 용매는 용질 주변을 감쌈
○ 용매가 물인 경우 수화(hydration)라고 함
⑵ 용액의 농도
① 질량%, 부피%
② 몰농도(M) : 용매 1 L당 용질의 몰수
③ 몰랄농도(m) : 용매 1 kg당 용질의 몰수
④ 몰분율(x) : 용매와 용질의 입자수 비
⑤ ppm, ppb
⑶ 용액의 종류
① 불포화용액 : 용질을 더 녹일 수 있는 용액
② 포화용액 : 최대의 용질이 녹아 있는 용액
③ 과포화용액 : 포화상태보다 더 많은 용질이 있는 용액, 용질이 석출됨
⑷ 전해질과 비전해질
① 전해질(electrolyte) : 물에 용해되었을 때 전기를 전도하는 물질
○ 전해질은 서로 반대 전하를 띠는 입자로 해리되어 있음
○ 예 : 소금, 황산구리 II
② 비전해질(non-electrolyte) : 물에 용해되었을 때 전기를 전도하지 않는 물질
○ 예 : 증류수, 에탄올, 설탕물
③ 강전해질 : 용질이 용액에서 이온화되는 정도가 높은 물질
○ 이온의 수가 많으면 강전해질에 해당
○ 예 : 이온결합 화합물(NaCl), 강산(HCl), 강염기(NaOH) 등
④ 약전해질 : 용질이 용액에서 이온화되는 정도가 낮은 물질
○ 이온의 수가 적으면 약전해질에 해당
○ 예 : 약산(CH3COOH), 약염기(NH4OH) 등
3. 용해도 [목차]
⑴ 용해의 기본 원리
① 용해엔탈피
○ ΔH용해, dissolution = ΔH격자 + ΔH수화 : M+(g) + N-(g) → M+(aq) + N-(aq)
○ ΔH격자, lattice (< 0) : M+(g) + N-(g) → MN(s)
○ 금속 이온의 반지름이 작을수록 격자엔탈피의 절댓값이 큼
○ ΔH수화, hydration (0 ± ) : MN(s) → M+(aq) + N-(aq)
② 수화 : 수용액에서 물 분자에 의해 둘러싸이는 현상
○ 이온성 용질 : 이온이 작을수록, 전하가 클수록 수화가 잘 일어남
○ 수화로 인해 물 분자가 질서 있는 상태가 되므로 용매의 엔트로피 감소
○ 수화로 인해 용질이 규칙적인 구조를 잃어버리므로 용질의 엔트로피 증가
○ 수화 과정은 엔트로피 증가 반응
○ 순수한 용매의 증발엔트로피 = S기체 - S용매 > S기체 - S용액 = 용액의 증발 엔트로피
⑵ 온도와 용해도
① 고체의 용해도 : 온도가 증가할수록 용해도 증가, 흡열반응(ΔH용해 > 0)
② 기체의 용해도(일부 고체도 해당) : 온도가 증가할수록 용해도 감소, 발열반응(ΔH용해 < 0)
③ 헨리의 법칙(Henry's law)
○ 수식화 : 용액 내 몰농도 (C) = 헨리 상수 (K) × 기체의 분압 (P)
○ 기체의 용해도는 기체의 부분압력에 비례한다고 기술
○ 비교적 용해도가 작은 기체에서만 성립
○ 헨리의 법칙 증명
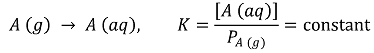
⑶ 극성과 용해도 : 끼리끼리 녹인다(like dissolves like)
① 극성 용매는 극성 용질을 잘 녹임
② 비극성 용매는 비극성 용질이 잘 녹임
4. 용액의 총괄성 [목차]
⑴ 정의
① 용질의 종류에 관계없이 용질의 입자수와 관련된 성질
② 이상용액이라는 가정 하에서 모든 총괄성에 원인이 되는 인자는 엔트로피
⑵ 반트호프인자(van't Hoff factor) : i로 표시
① 정의

② 예 : NaCl (s)를 물에 넣으면 Na+(aq)와 Cl-(aq)로 완전히 분리되므로 반트호프인자는 2
③ 실제 용액 : 농도가 진할수록, 이온의 전하량이 클수록 용액 내에서 더 많은 이온쌍을 형성하므로 i가 작아짐
④ 이온화도와 반트호프인자
⑶ 증기압 내림
① 라울의 법칙(Raoult's law)
○ 내용 1. 평형상태에서 각 성분의 부분압력은 액체 혼합물의 몰 분율에 비례
○ 내용 2. 혼합물의 부피는 혼합하기 전의 각 성분의 부피의 합과 같음
○ 내용 3. 혼합물의 분자간 상호작용은 순수 성분에서의 분자간 상호작용과 동일
○ 관련 수식
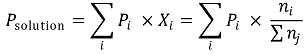
② 용매와 용질이 모두 증기압을 형성할 때
③ 이상용액(↔ 비이상용액) : 라울의 법칙을 만족하는 용액
Figure. 1. 라울의 법칙과 양의 편차, 음의 편차
○ P용액 = P이상용액 : ΔH용해 = 0
○ P용액 < P이상용액 : 용매가 증기가 되기를 싫어해 증기압 감소 ⇔ 용질-용매 상호작용 강함 ⇔ ΔH용해 < 0
○ P용액 > P이상용액 : 용매가 증기가 되려는 경향이 강해 증기압 증가 ⇔ 용질-용매 상호작용 약함 ⇔ ΔH용해 > 0
④ 이상용액의 분별증류 : 이상용액은 액체상과 기체상의 조성이 다름 → 기화, 액화를 반복시 순수 성분 추출 가능
⑷ 끓는점 오름 : 1차 근사이므로 묽은 용액, 작은 온도변화에서만 성립
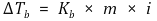
⑸ 어는점 내림 : 1차 근사이므로 묽은 용액, 작은 온도변화에서만 성립
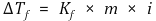
① 몰랄 내림 상수 Kf는 용질이 아니라 용매의 속성
② 몰랄 내림 상수 Kf는 근사값이므로 온도 범위가 달라지면 기존 상수값을 사용할 수 없을 수도 있음
⑹ 삼투현상(osmosis)
① 삼투
○ 반투막을 사이에 두고 농도가 다른 두 용액이 있을 때 용매 분자의 알짜 이동이 생기는 현상(자유물분자의 확산)
○ 삼투압(osmotic pressure)
○ 삼투 현상이 일어나지 않도록 가해주어야 하는 압력
○ 반트호프 법칙에 의해 수식화
π = CRT × i
○ 용질의 농도에 비례하여 용매(e.g., 물)를 끌어당기는 힘으로 이해할 수 있음
○ 삼투압 식이 이상기체상태방정식과 유사한 이유 : 용액 속 용질 분자가 묽기 때문에 이상기체처럼 작용
② 역삼투
○ 삼투압보다 큰 압력을 가해주면 물이 고농도에서 저농도로 이동하는 현상
○ 역삼투에서 이론적으로 필요한 압력 = 원하는 만큼의 물이 제거되어 삼투압이 증가된 경우 평형을 이룰 수 있는 압력
○ 역삼투 예제
5. 콜로이드 [목차]
⑴ 개요
① 정의 : 1 ㎚ ~ 1,000 ㎚의 미립자가 기체 또는 액체 중에 분산된 것
② 기체 중에 분산된 것을 에어로졸(aerosol)이라고 함
⑵ 성질 : 입자의 크기
① 틴들 현상(틴달 현상, Tyndall phenomenon)
○ 정의 : 콜로이드 내 입자들로 인해 입사한 빛의 궤도가 보이는 것
○ 레일리 산란과 유사하게 특정 파장대를 산란시키지만 레일리 산란 조건 및 산란 궤도가 상이함
○ 현재까지 틴들 현상을 정확하게 기술하는 수학적 공식은 없음
② 투석 : 반투과성 막을 통과할 수 있는 물질의 확산
○ 투석액 농도 > 용액 농도 : 투석액에서 용액으로 해당 물질 이동
○ 투석액 농도 = 용액 농도 : 물질 이동 없음
○ 투석액 농도 < 용액 농도 : 용액에서 투석액으로 해당 물질 이동
○ 신장 혈액투석이 대표적
③ 흡착(adsorption)
○ Freundlich adsorption isotherm equation
○ Langmuir adsorption isotherm equation
④ 브라운 운동(Brownian motion)
○ 개요
○ 정의 : 용액 내 미립자들의 랜덤워크 운동
○ 아인슈타인이 노벨상을 받은 분야
○ 평균 자유 경로(mean free path)
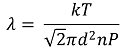
○ k : 볼츠만 상수
○ T : 절대 온도
○ d : 분자의 직경
○ n : 단위 부피당 분자의 수
○ P : 압력
○ 제곱 평균 제곱근 속력 : 단원자 기체 혹은 자유도가 3인 기체의 경우 다음과 같음
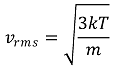
○ m : 분자량
○ 분자 간 충돌까지의 평균 시간
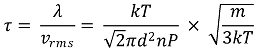
○ 응용 : DLS(dynamic light scattering)는 브라운 운동을 반영하는 산란광을 측정하여 입자의 크기를 측정함
○ 1st. time-intensity plot을 그림
Figure. 2. DLS setting 및 intensity-time plot
○ 2nd. 두 개의 intensity-time plot을 cross-correlation을 하여 delayed time-correlation function plot을 그림
Figure. 3. delayed-correlation function plot
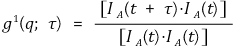
○ 3rd. exponential decay curve를 분석하여 translational diffusion coefficient Dt를 구함
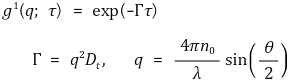
○ 4th. Stokes-Einstein law에 따라 hydrodynamic diameter Dh를 계산함
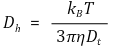
⑶ 성질 : 전하
① 전기영동
② 제타 전위 또는 제타 포텐셜(zeta potential)
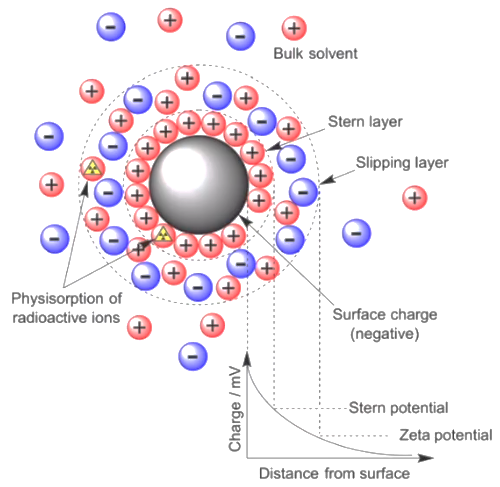
Figure. 5. 입자의 종류에 따른 제타 전위 양상
○ 배경이론
○ 하전된 입자 주위로 반대 극성의 입자가 모여 1차적인 껍질을 형성함
○ stern layer : 1차적인 껍질
○ 1차적인 껍질 주위로 관련된 극성의 입자가 모여 2차적인 껍질을 형성함
○ stern layer는 입자를 따라 움직임
○ double layer : 2차적인 껍질. DEL(double electrode layer)라고도 함
○ 2차적인 껍질은 처음 입자와 같은 극성일 수도 있고 다른 극성일 수도 있음
○ 입자보다 용매의 영향에 의해 움직임
○ 제타전위(zeta potential)
○ 정의 : double layer의 표면의 전위
○ surface potential, stern potential과 달리 측정 가능
○ 전위를 가했을 때 입자의 이동속도의 차이를 통해 제타전위를 측정할 수 있음
○ 유용성 1. 입자의 polarity를 측정할 수 있음
○ 유용성 2. 전하 상태뿐만 아니라 입자 분산 정도도 반영함
○ 두 입자가 같은 부호이고 충분히 큰 제타 전위를 가지면 서로 응집하지 않음
○ 제타 전위의 절대값이 30 mV를 넘으면 입자들 간에 반발력이 우세하게 작용하여 응집하지 않음
○ 이유 : 척력이 발생하기 때문
③ 엉김(응집, flocculation)
○ 콜로이드 입자가 입자 사이의 정전기적 인력으로 모여 작은 덩어리를 만드는 현상
○ 엉김은 용질과 염이 같이 침전된다는 점에서 염석과 구별됨
○ Schulze-Hardy (S-H) rule : 응집력은 용질 간의 정전기적 인력에 비례. 약 125년 전에 제안됨
○ 요인 1. 이온의 농도 : 양전하 용질과 음전하 용질이 모두 많을수록 응집이 빠르게 일어남
○ 요인 2. 용질의 전하가 클수록 응집력이 큼
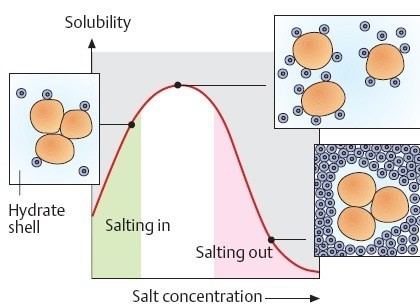
④ 염석(salting-out)
○ 염석은 용질만 침전된다는 점에서 엉김과 구별됨
○ 저농도 염 : 염이 첨가될수록 용해도 증가 (salting-in). 염들로 인한 물질 변성이 물의 침투를 돕기 때문
○ 고농도 염 : 염이 첨가될수록 용해도 감소 (salting-out). 염들이 물질을 둘러싸 물과의 상호작용을 감소시키기 때문
○ 표적 물질의 양이 많을수록 용해도의 피크값이 커짐
○ 정제의 초기수단이며 황산암모늄을 많이 사용
○ 응용 : 두부를 만들 때 간수(MgCl2)를 넣음
입력: 2018.12.30 20:39
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 13-1강. 열역학 과정과 카르노 순환 (8) | 2018.12.27 |
|---|---|
| 【화학】 13강. 열역학 (42) | 2018.12.27 |
| 【화학】 10강. 액체와 고체 (4) | 2018.12.27 |
| 【화학】 12강. 혼합물의 분리 (0) | 2018.12.27 |
| 【화학】 9강. 기체 (2) | 2018.12.27 |







최근댓글