13강. 열역학(thermodynamics)
추천글 : 【화학】 화학 목차
a. 심화 열역학
1. 계와 주위 [목차]
⑴ 계의 정의
① 계(system) : 관심의 대상이 되는 것, 화학 반응에서 반응물과 생성물
② 주위(surrounding) : 계를 제외한 나머지 공간
③ 우주(universe) : 계와 주위를 통츨어 지칭
⑵ 계의 분류
① 열린계(open system) : 물질, 에너지 출입이 있는 계
② 닫힌계(closed system) : 에너지만 출입 가능
③ 고립계(isolated system) : 주위와 아무런 상호작용을 하지 않는 경우
⑶ 계의 조건
① 온도
○ 섭씨온도 : 정상 대기압 하에서 물이 어는점을 0 ℃, 물이 끓는점을 100 ℃로 둔 온도눈금
○ 화씨온도 : 정상 대기압 하에서 물이 어는점을 32 ℉, 물이 끓는점을 212 ℉로 둔 온도눈금
○ 절대온도 : 정상 대기압 하에서 물이 어는점을 273.15 K, 물이 끓는점을 373.15 K로 둔 온도눈금
○ Rankine 온도 : 정상 대기압 하에서 물이 어는점을 0 ℉, 물이 끓는점을 180 ℉로 둔 온도눈금
② 압력
③ 표준상태(STP, standard temperature and pressure) : 0 ℃, 1 atm
○ 기체 1몰의 부피 = 22.4 L
④ SATP(standard ambient temperature and pressure) : 25 ℃, 1 bar
○ 기체 1몰의 부피 = 24.79 L
⑤ NTP(normal temperature and pressure) : 20 ℃, 1 atm
⑥ ATP(actual temperature and pressure) : 실제 온도와 실제 기압
⑦ 온도와 압력의 측정
○ Bayard-Alpert pressure gauge : 기체를 이온화하여 전류를 측정, 저압 조건에서 압력 측정에 이용
○ capacitance manometer : 최고급 타이어를 제작할 때 사용
⑶ 열역학
① 반응물과 생성물의 에너지, 자발성 등을 기술하는 학문
② 열역학 법칙
○ 열역학 제1법칙 : 에너지 보존 법칙, 고립계의 내부에너지는 일정
○ 제1종 영구기관 : 없는 에너지를 만드는 영구기관
○ 열역학 제2법칙 : 무질서도 증가의 법칙, 반응의 자발성·방향성 예측
○ 제2종 영구기관 : 가능하지 않은 에너지 변환을 하는 영구기관
○ 열역학 제3법칙 : 절대영도에서 완전결정의 절대 엔트로피는 0
○ 열역학 제0법칙 : 등가온도의 정의
○ 법칙의 필요성 : 온도에는 정의가 없음. 그저 상대적인 척도로서 에너지가 흐르는 방향을 표시
○ 내용 : 열적 평형(thermal equilibrium)에서 TA = TB, TB = TC → TA = TC
⑷ 상태함수, 경로함수
① 상태함수(state function) : 오직 현재 상태와만 관련 있는 물리량
○ 예 : 내부에너지
② 경로함수(path function) : 상태가 변하는 과정에 영향을 받는 물리량
○ 예 : 열, 일
2. 열역학 제1법칙 [목차]
⑴ 에너지
① 일 = 힘 × 거리
② 에너지 : 일을 할 수 있는 능력
⑵ 내부 에너지(e) : 계를 이루는 모든 입자의 역학적 에너지의 총합
① 기체의 내부에너지는 온도에 대한 상태함수
○ 내부에너지가 온도에 대한 함수임을 증명
○ 내부에너지가 상태함수인 이유 : 역학적 에너지가 상태함수이기 때문
② 에너지 등분배 법칙(energy equipartition law)
○ 정의 : 한 개의 기체 분자들은 한 자유도마다 평균적으로 ½ kBT의 에너지를 가짐
○ 자유도 : 기체 분자가 에너지를 가질 수 있는 독립된 방법의 수
○ 병진운동에너지(translational energy)
○ 회전운동에너지(rotational energy)
○ 진동운동에너지(vibrational energy)
③ 단원자 기체(monoatomic gas)
○ 자유도는 총 3개 : x축, y축, z축 병진운동에너지
○ 단원자 분자 이상 기체의 분자 1개의 평균 운동 에너지
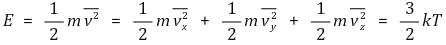
④ 이원자 기체(diatomic gas)
○ 자유도는 총 5개 : x축, y축, z축 병진운동에너지, x축, y축 회전운동에너지
○ 이원자 분자 이상 기체의 분자 1개의 평균 운동 에너지
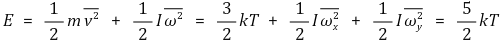
⑤ angular triatomic gas
○ 자유도는 총 6개 : x축, y축, z축 병진운동에너지, x축, y축, z축 회전운동에너지
○ angular triatomic gas 분자 1개의 평균 운동 에너지

⑥ 다원자 기체
○ 자유도는 총 7개 : x축, y축, z축 병진운동에너지, x축, y축, z축 회전운동에너지, 진동운동에너지
○ 다원자 분자 이상 기체의 분자 1개의 평균 운동 에너지
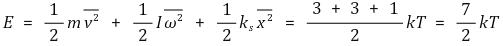
○ 다원자 기체의 온도별 정적 몰비열의 양상

Figure. 1. 다원자 기체의 온도별 정적 몰비열의 양상
⑦ 뒬롱-프티의 법칙(law of Dulong and Petit)
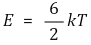
○ 고체 원자가 평형점 둘레를 조화진동하고 있다고 가정
○ 고전 통계역학에서만 성립. 양자 통계역학에서 불성립
⑶ 일(w) : 기체가 팽창할 때 외부로 전달되는 에너지의 형태
① 정의 : 방향성이 있는 에너지
○ 물리에서는 주위로의 일을 양으로 정의. 화학에서는 주위로의 일을 음으로 정의. 여기선 후자 채택
○ 물리는 계가 주위와 상호작용하는 데 관심이 많고, 화학은 계 자체에 관심이 많기 때문
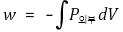
② 등온가역적 팽창
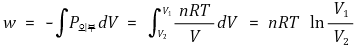
③ 외부 압력이 일정할 때

④ 자유팽창 : 외부 압력이 0이므로 0
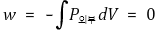
⑷ 열(q)
① 정의 : 방향성이 없는 에너지
② 열역학 제1법칙 : 내부 에너지, 일, 열의 관계
○ q = qin임을 주의하자.
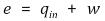
③ 열과 관련된 용어
○ 발열반응(exothermic process)
○ 흡열반응(endothermic process)
○ 단열벽(adiabatic wall)
○ 투열벽(diathermic wall)
④ 열용량(heat capacity)
○ 열량 : 열의 양적인 크기. Q (단위 : cal, J 등)
○ 열용량(heat capacity) : 단위 온도만큼 올리기 위해 필요한 열량. C (단위 : cal/℃, J/K 등)
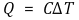
○ specific heat capacity : 단위 질량당 열용량. Cs = C/m (단위 : kJ/kg·℃)
○ molar heat capacity : 1몰당 열용량. Cm = C/n (단위 : kJ/mol·℃)
○ 몰 정적열용량 : 1 ℃ 당 일정한 부피에서 전달된 열
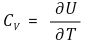
○ 몰 정압열용량 : 1 ℃ 당 일정한 압력에서 전달된 열
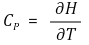
○ 정적열용량과 정압열용량의 관계식
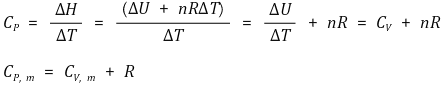
○ 기체의 몰 열용량 : 온도 T (단위 : K), 열용량 Cp (단위 : cal/g-mol·K)에 대하여
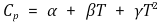
| α | β × 103 | γ × 106 | |
| CH4 | 3.381 | 18.044 | -4.30 |
| C2H6 | 2.247 | 38.201 | -11.049 |
| CO2 | 6.214 | 10.396 | -3.545 |
| H2O | 7.256 | 2.298 | 0.283 |
| O2 | 6.148 | 3.102 | -0.923 |
| N2 | 6.524 | 1.25 | -0.001 |
Table. 1. 기체의 몰 열용량
○ (참고) 위 식에서 단위가 cal/g-mol·K인 이유는 연료 + 공기의 전체 질량을 1 g으로 두고 계산하겠다는 의미
⑤ 열량계
○ 봄베 열량계 (통 열량계) : 부피를 일정하게 유지하여 일을 0으로 하고 열량을 측정하는 것
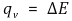
○ 간이 열량계 : 압력을 일정하게 유지하여 열량을 측정하는 것
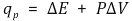
○ (참고) 교축 열량계 : 교축과정에서 엔탈피가 일정할 때 증기건도를 측정하는 것
⑸ 엔탈피
① 개요
○ 정의 : 내부에너지에 일 개념을 추가한 것
○ 엔탈피는 압력이 일정하지 않아도 정의될 수 있음
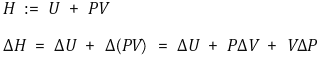
○ 압력이 일정한 경우 엔탈피는 출입한 열과 같음
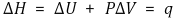
○ 엔탈피는 비팽창일이 없는 경우 열과 같음
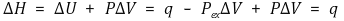
○ (주석) 엔탈피가 등압조건에서만 정의된 것으로 이해했으나 다음 식을 보고 생각이 바뀜
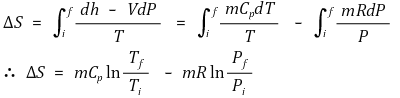
② 특징
○ 상태함수 : 엔탈피는 오직 온도에 대한 함수. 처음과 나중의 온도만 같으면 일정
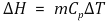
○ 엔탈피는 절대값이 없어서 엔탈피 변화량이 중요
○ 반응이 역으로 진행되면 ΔH의 부호가 반대가 됨
○ 크기성질 : 물질의 양에 비례
○ 등압조건에서 간이 열량계로 측정 : CP는 정압비열이지만 dh = mCPdT임은 압력이 일정하지 않아도 성립함
③ 반응 엔탈피
○ 생성 엔탈피(ΔHf) : 안정한 홑원소 물질로부터 물질 1몰이 만들어질 때의 반응 엔탈피
○ 공식 1. 동핵 이원자 기체(예 : O2(g))의 생성 엔탈피 = 0
○ 공식 2. 금속결정 (예 : Mg(s))의 생성 엔탈피 = 0
○ 분해 엔탈피(-ΔHf) : 물질 1몰이 안정한 홑원소 물질로 분해될 때의 반응 엔탈피
○ 결합 엔탈피(ΔHD) : 어떤 물질 1몰이 그 물질을 구성하고 있는 원자들의 기체상으로 분해될 때의 반응 엔탈피
○ 결합이 분해되는 반응은 흡열반응
○ 연소 엔탈피(ΔHC) : 어떤 물질 1몰을 완전히 연소시킬 때의 반응 엔탈피
○ 용해 엔탈피
○ ΔH용해 = ΔH격자 + ΔH수화
○ ΔH용해 : MN(s) → M+(aq) + N-(aq)
○ ΔH격자 (> 0) : MN(s) → M+(g) + N-(g)
○ 금속 이온의 반지름이 작을수록, 각 이온의 개별전하가 클수록 격자엔탈피의 절댓값이 큼
○ ΔH수화 (< 0) : M+(g) + N-(g) → M+(aq) + N-(aq)
○ 표준 반응 엔탈피(ΔHº) : 표준 상태에서의 반응 엔탈피
○ 기체 상태의 물질의 표준 상태는 압력 1 atm, 온도 25 ℃ (298.15 K)인 순수한 기체
○ 액체, 고체 상태 순물질의 표준 상태는 순수한 액체 또는 고체
○ 용액의 표준 상태는 농도가 1 M인 용액
○ 원소의 표준 상태는 1 atm에서 그 원소가 존재하는 상태
○ 표준 생성 엔탈피

○ 표준 결합 엔탈피

○ 표준 연소 엔탈피

④ 본-하버 순환(Born-Haber cycle)
○ 본-하버 순환 : 이온 화합물의 생성을 설명하기 위한 가상의 반응 경로
○ 헤스의 법칙(Hess's law) : 엔탈피가 상태함수이기 때문에 어떤 경로를 거쳐도 반응물과 생성물이 동일하면 ΔH 동일
⑤ 기타
○ 가열 곡선에서의 기울기
○ 고체 : 분자간 인력이 거의 안 끊어지므로 열이 운동에너지로 전달
○ 액체 : 분자간 인력을 끊는 데에도 일부의 에너지가 사용. 기울기가 가장 작음
○ 기체 : 분자간 인력이 없음. 열이 운동에너지로 전달. 기울기가 가장 큼
○ 내부에너지와의 관계
○ 기체 반응 : 반응물과 생성물의 기체 몰수비 변화가 없으면 ΔH = ΔU
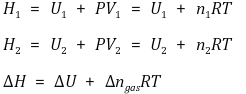
○ 액체, 고체의 반응은 등압과정으로 간주할 수 있고, 일은 거의 없으므로 ΔH = ΔU
⑴ 개요
① 엔트로피(entropy) : 무질서도를 나타내는 상태함수
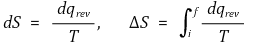
② 가역과정(reversible process) : 전체 엔트로피 변화가 0인 과정
③ 열역학 제2법칙은 다음과 같이 총 네 가지 표현으로 표현할 수 있음
⑵ 표현 1
① 자발적 변화 : 외부 영향 없이 일어나는 변화
② 법칙 : 자발적 변화는 우주의 엔트로피가 증가하는 방향으로 진행
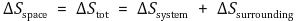
③ 주위 엔트로피 ΔS주위 : 반응의 가역·비가역과 무관
○ 주목하는 계와 그 주위가 고립된 계를 이루면 비로소 열역학 제2법칙을 적용할 수 있음
○ 주위 엔트로피 ΔS주위의 계산 : 반응의 가역·비가역과 무관. 주위가 일정한 온도·압력이라고 가정

○ ΔS주위가 위와 같이 단순하지는 않겠지만 시스템으로 도출할 수 있는 값들로 구성된다는 점에서 중요
④ 결론 : ΔS전체>0이면 자발적, ΔS전체<0이면 비자발적
⑶ 표현 2 : 클라우지우스 부등식(Clausius inequality)
① 클라우지우스의 표현 : 열은 고온에서 저온으로 흘러감. 자발적으로 저온에서 고온으로 흘러가지 못함
② 수식화 (단, 등호조건은 가역과정일 때)
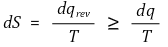
③ 증명
○ 계에 일을 하는 만큼 외부 압력이 같이 상승해 주어야 더 많은 일을 할 수 있음
○ 그래서 가역조건은 비가역조건보다 주위에 많은 일을 함

○ 가역과정과 비가역과정의 처음과 나중 상태가 같다면 다음과 같음 (물리적 표현을 적용)

○ 그러므로 다음 식을 얻는다.
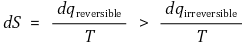
④ 열역학 제2법칙 도출 : 만약 계가 주위로부터 고립된 경우 dq = 0이므로 dS ≥ 0
⑤ 자유팽창
○ 자유팽창과 등온팽창은 직관적으로 엔트로피 변화가 동일함
○ 자유팽창의 경우 열의 출입이 없음
○ 자유팽창의 경우 가역과정이 아니기 때문에 위의 공식을 적용하면 안 됨
⑷ 표현 3 : 카르노기관에서 서술
① 켈빈-플랑크의 표현 : 외부에서 흡수한 열을 전부 일로 바꾸는 열기관을 만들 수 없음
② 즉, 열효율이 100%인 열기관을 만들 수 없음
③ 카르노 기관의 효율은 70%임 : 100의 열이 있으면 70만큼만 일로 전환할 수 있음
⑸ 표현 4. 통계역학적 정의
① 볼츠만(Boltzmann) 식에 의해 정의되므로 볼츠만 엔트로피라고도 부름
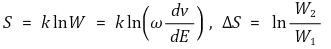
② 상태수 W : 전체 에너지를 일정하게 유지시키면서 계의 분자들을 배치시킬 수 있는 방법의 수
○ 위치적 확률 : 분자배열이 무질서할수록 해당 경우의 수가 많아 그 방향으로 반응 진행
○ 분자의 운동상태 : 서로 다른 에너지 준위에서 분자배열 시 해당 경우의 수가 많아 더 선호 → 온도가 높을수록 엔트로피가 커짐
○ 엔트로피의 절대값과 0의 엔트로피를 정의할 수 있음 → 열역학 제3법칙
③ 열역학적 정의와 통계역학적 정의의 등가성 증명
○ 단일 분자에 주어지는 미시적 상태수가 부피에 비례한다고 가정

○ N개 분자에 대해서 전체 상태수는 다음과 같이 나타남

○ 이상기체가 V1에서 V2로 등온팽창할 때 통계역학적 엔트로피는 다음과 같음
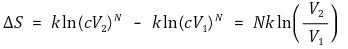
○ 결국 통계적 엔트로피의 정의는 열역학적 엔트로피의 정의와 동등
○ 볼츠만이 열역학적 정의에서 심오한 의미를 끄집어 내기 위해 역계산을 했던 것으로 추정됨
④ 고전통계역학과 양자통계역학
○ 고전통계역학 : 볼츠만이 시작한 열역학적 개념
○ 양자통계역학 : 오비탈 이론으로 대표되는 양자역학적 개념
⑹ 엔트로피의 적용
① 적용 1. 일반 열역학과정
② 적용 2. 기체 반응의 엔트로피 변화 예측
○ 반응 엔트로피 ΔS : 기체 분자의 수가 증가하는 반응에서 ΔS > 0
③ 적용 3. 진공에서의 팽창
○ (참고) ΔT=0, W=0 → Q=0
○ 열역학적 정의가 적용되지 않는 상황
○ 통계역학적 정의대로 상태수 개념으로 접근하면 등온팽창과 다름이 없으므로
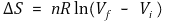
④ 적용 4. 상전이 엔트로피
○ 일정 압력 하에서 상전이 온도 T전이는 일정하고, Qp=ΔH이므로
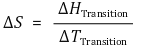
○ 표준 상전이 엔트로피 ΔSº : 표준 상태(1 bar)에서 전이가 일어났을 때의 상전이 엔트로피
○ Trouton 규칙 : 대부분의 액체 표준 증발 엔트로피가 약 85 J/K로 비슷
○ 물의 경우 ΔSºvap가 큰 편 (∵ 액체상 물의 엔트로피가 작기 때문)
| 액체 | 정상 끓는점 (K) | ΔSº (J/K·mol) |
| 아세톤(acetone) | 329.4 | 88.3 |
| 암모니아(ammonia) | 239.7 | 97.6 |
| 아르곤(argon) | 87.3 | 74 |
| 벤젠(benzene) | 353.2 | 87.2 |
| 에탄올(ethanol) | 351.5 | 124 |
| 헬륨(helium) | 4.22 | 20 |
| 수은(mercury) | 629.7 | 94.2 |
| 메탄(methane) | 111.7 | 73 |
| 메탄올(methanol) | 337.8 | 105 |
| 물 | 373.2 | 109 |
Table. 2. 정상 끓는점에서의 액체 표준 증발 엔트로피
⑤ 적용 5. 시간이 한쪽 방향으로만 흐르는 이유는 열역학 제2법칙과 관련 있음
4. 열역학 제3법칙 [목차]
⑴ Nernst의 열 정리
① 표현 1. 물리적이나 화학적 변화에 수반되는 엔트로피 변화는 절대영도로 접근함에 따라 0으로 접근
② 표현 2. 모든 완전한 결정 물질의 엔트로피는 T=0에서 0임
⑵ 잔류 엔트로피
① T=0에서 실제로 측정되는 엔트로피
② 예 1. CO의 잔류 엔트로피 : random orientation이 비교적 자유로워 잔류 엔트로피 ↑
○ CO분자 두 개를 고려할 때 CO ··· CO와 CO ··· OC로 두 가지 두 개의 배열이 가능하다. Boltzmann의 통계역학적 정의에 의해 S = k ln W = k ln(2×2)= k ln 4만큼의 절대 엔트로피를 가지게 된다. 이를 1몰(6.02 × 1023개)로 확대하면 이때 예측되는 잔류 엔트로피는 S = NAk ln 2 = 5.76 (J/K)이 된다. 실제 측정값은 4.6 (J/K)으로 꽤 유사한 값이 나온다.
③ 예 2. HCl의 잔류 엔트로피 : arrangement가 한 종류만 가능하여 잔류 엔트로피가 0에 가까움
⑶ 표준 몰 엔트로피
① 절대 영 : 0 K에서 순수한 고체 결정의 엔트로피를 0으로 정의
② 물질의 표준 몰 엔트로피 계산
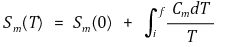
③ 특징 1. Sm(s) < Sm(ℓ)< Sm(g) : 고체에서 기체로 갈수록 더 무질서해지므로
④ 특징 2. 무거운 원소의 몰 엔트로피가 가벼운 원소보다 높음
⑤ 특징 3. 크고 복잡한 화학종은 작고 단순한 화학종보다 몰 엔트로피가 높음
⑥ 25 ℃에서의 표준 몰 엔트로피
| 기체 | Sº | 액체 | Sº | 기체 | Sº |
| 암모니아 (NH3) |
192.4 | 벤젠 (C6H6) |
173.3 | 산화칼슘 (CaO) |
39.8 |
| 이산화탄소 (CO2) |
213.7 | 에탄올 (C2H5OH) |
160.7 | 탄산칼슘 (CaCO3) |
92.9 |
| 수소 (H2) |
191.6 | 물 (H2O) |
69.9 | 다이아몬드 (C) |
2.4 |
| 질소 (N2) |
191.6 | 그래핀 (C) |
5.7 | ||
| 산소 (O2) |
205.1 | 납 (Pb) |
64.8 |
Table. 3. 25℃에서 물질들의 표준 몰엔트로피(J/K·mol)
⑷ 표준 반응 엔트로피
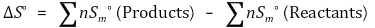
5. 깁스 자유에너지(G, Gibbs free energy) [목차]
⑴ 정의 : 반응의 자발성을 나타내는 상태함수
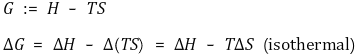
① 열역학 제2법칙을 적용하려면 계와 주위를 모두 고려해야 하므로 번거로움
② 깁스 자유에너지는 반응의 자발성을 판단하기 위해 계의 성질만 사용하면 되므로 용이함
○ (참고) 계의 성질과 주위의 성질을 따로 고려하면 계산과정이 많아짐
③ 의미 1. ΔG < 0이면 자발적인 반응, ΔG > 0이면 비자발적인 반응, ΔG = 0이면 평형
④ 의미 2. 일정한 온도, 압력 조건에서 자발적인 반응이 일어날 때 반응으로부터 얻을 수 있는 최대 비팽창일
⑤ 한계 : 주위의 엔트로피 변화가 그렇게 단순하지는 않음
⑵ 증명
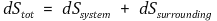
일정한 온도와 압력에서 dq = dH, dq주위 =-dH이므로 위 식은 다음과 같이 변한다.
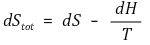
양변에 -T를 곱해주면 깁스 자유에너지 식을 얻는다.
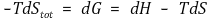
자발적인 반응은 dS전체 > 0이므로
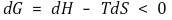
⑶ 물리적 의미 : ΔG = 최대 비팽창일
① 전기화학과 깁스 자유 에너지 (단, E = 환원전위)
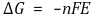
⑷ 자유에너지 변화 ΔG와 표준 자유에너지 변화 ΔG˚의 관계
① 수식화
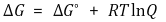
○ 위 수식은 등온과정에서만 성립하는 식 : 단, 이를 벗어나기 위해 반트호프 식이 사용됨
○ ΔGº은 표준 상태의 자유에너지 변화를 의미하지만, 임의의 기준 상태로 두어 문제를 푸는 경우도 가끔 존재함
○ ΔG = 0인 경우, 반응지수 Q는 평형상수 K로 치환될 수 있음
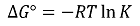
② 증명
○ 몰수를 n, 1몰당 깁스 자유에너지를 Gm이라고 하면 ΔG는 다음과 같이 정의됨
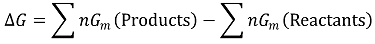
○ 기체의 예 (단, 등온과정)
○ 자유에너지 변화는 최대 비팽창일과 같음

○ 1번 상태를 표준상태(즉, P1 = 1)라고 하면 다음과 같음
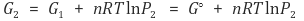
○ 양변을 n으로 나눠주면 다음과 같음
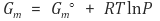
○ 자유에너지는 절댓값이 없으므로 임의의 기준점에 대한 변화량으로 계산
○ 용액의 예 (단, 등온과정)
○ 삼투압 공식에 따르면 압력과 농도는 다음과 같은 관계를 가짐 (단, C는 몰농도)
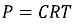
○ 따라서 다음과 같은 관계식을 얻음
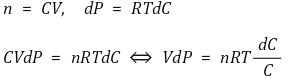
○ 최종적으로 다음과 같은 결론을 얻음
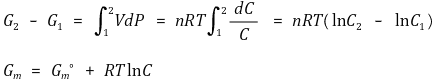
○ 활동도(activity)라는 개념으로 기체와 용액의 경우를 통합할 수 있음
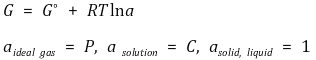
○ 화학반응에 적용하면 다음이 도출
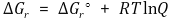
③ 해석
○ 임의의 시점의 자유에너지 변화 ΔGr와 표준 자유에너지 ΔGrº의 관계

○ 표준 생성 자유에너지 ΔGrº : 표준 상태에서 생성물 1몰이 만들어질 때의 자유에너지 변화
○ ΔGrº<0 : 표준 상태에서 정반응이 자발적, K>1
○ ΔGrº>0 : 표준 상태에서 역반응이 자발적, K<1
○ ΔGrº = 0 : 표준 상태에서 평형에 도달, K = 1
○ 반응지수 Q와 평형상수 K의 관계
○ Q>K : 역반응 진행
○ Q = K : 평형
○ Q<K : 정반응 진행
○ 반응경로 - 자유에너지 곡선

Figure. 2. 반응경로 - 자유에너지 곡선
○ 반응경로 - 자유에너지 곡선의 기울기는 ΔGr
○ 생성물이 없는 반응 초기는 정반응이 진행되므로 ΔGr < 0
○ Gr은 반응이 진행될수록 커지다가 (∵ Q 증가) ΔGr = 0인 지점(정반응 = 역반응)에서 평형상태가 됨
○ 평형지점은 기울기가 0인 지점
④ 응용 : 반트호프 방정식(van't Hoff equation)
○ 도입 : 등온 과정 제약을 벗어나기 위해 선형 근사를 통해 자유에너지 변화를 추정
○ 가정 : ΔHº와 ΔSº가 온도에 따라 일정함
○ 수식화
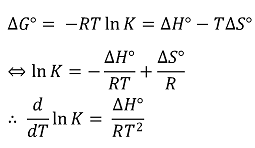
○ 포인트. 위 수식에서도 Δ(TS)가 아니라 TΔS라고 돼 있는 것은 등온과정 제약이 일부 반영된 것
○ 예제
⑸ 자유에너지 변화 ΔG와 반응속도의 관계
① (참고) Brønsted-Evans-Polanyi (BEP) 원리 : 자유 활성화 에너지와 반응의 자유 에너지가 비례
② 위 원리는 하몬드 가설처럼 경험칙인 것으로 보임
입력: 2019.01.09 13:33
수정: 2023.01.05 00:35
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 14강. 산화환원반응 (0) | 2018.12.27 |
|---|---|
| 【화학】 13-1강. 열역학 과정과 카르노 순환 (8) | 2018.12.27 |
| 【화학】 11강. 용액 (0) | 2018.12.27 |
| 【화학】 10강. 액체와 고체 (4) | 2018.12.27 |
| 【화학】 12강. 혼합물의 분리 (0) | 2018.12.27 |



최근댓글