17강. 화학평형
추천글 : 【화학】 화학 목차
1. 평형상태 [목차]
⑴ 평형상태 : 정반응과 역반응의 속도가 같아 화학종의 농도가 더 이상 변하지 않는 상태
① homogeneous : 모든 반응물과 생성물이 같은 상태인 경우
② heterogeneous : 둘 이상의 상태가 공존하는 경우
⑵ 평형상수(equilibrium constant) : 평형상태에서 일정하게 유지되는 상수

① 농도 평형상수 KC : 용액의 경우 몰농도로 평형상수 계산

② 압력 평형상수 KP : 기체의 경우 압력 평형상수를 사용

③ 열역학적 평형상수 K : 활동도(activity)라는 개념을 도입
○ 기체의 활동도
aideal gas = P ÷ Pº, Pº = 1 atm
⇔ aideal gas = P (단위 없음)
○ 용액의 활동도
asolution = C ÷ Cº, Cº = 1 M
⇔ asolution = C (단위 없음)
○ 고체, 기체의 활동도
asolid = aliquid = 1
○ 열역학적 평형상수
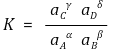
○ 평균 활동도 계수 γ : 각 이온들의 활동도 계수들의 기하 평균
○ 예 : CaCl2의 평균 활동도 계수 = (γCa2+ × γCl-)1/3
⑶ 평형상수 유도 1. 열역학적 해석
우선 A, B, C, D의 각각의 자유에너지는 다음과 같이 표현된다.
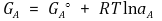
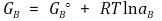
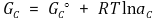

또한 반응의 자유에너지 변화는 다음과 같이 표현된다.
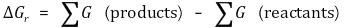
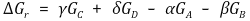
따라서 다음과 같은 결론을 얻는다.
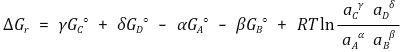
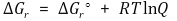
평형상수 K에 대하여 다음 식이 성립한다.
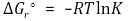
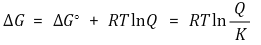
ΔGº이 일정하므로 K도 일정하다.
⑷ 평형상수 유도 2. 반응속도론적 해석
정반응 속도상수가 k1이고 역반응 속도상수가 k-1이라면 반응속도식은 다음과 같다.
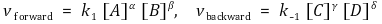
평형상태에서 정반응 속도와 역반응 속도가 같으므로 다음과 같다.
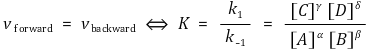
보충. 평형상태에서는 단일단계 반응처럼 간주하고 반응속도 식을 세울 수 있음
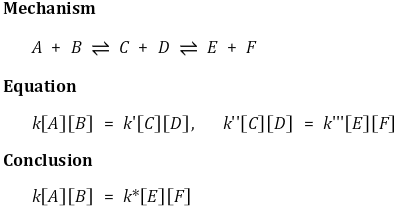
⑸ 반응지수 Q : 어떤 임의의 순간에 반응의 진행 정도를 나타내는 상수
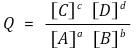
① 임의의 시점의 자유에너지 변화 ΔGr와 표준 자유에너지 ΔGrº의 관계

○ 표준 생성 자유에너지 ΔGrº : 표준 상태에서 생성물 1몰이 만들어질 때의 자유에너지 변화
○ ΔGrº < 0 : 표준 상태에서 정반응이 자발적, K>1
○ ΔGrº > 0 : 표준 상태에서 역반응이 자발적, K<1
○ ΔGrº = 0 : 표준 상태에서 평형에 도달, K = 1
② 반응지수 Q와 평형상수 K의 관계
○ Q > K : 역반응이 자발적
○ Q < K : 정반응이 자발적
○ Q = K : 평형상태
⑹ 반응식의 가감승제
① 규칙 1. 평형상수가 K0화학반응식에 계수 k를 곱하면 평형상수 K = K0k가 됨
② 규칙 2. 평형상수가 K1인 반응식과 K2인 반응식을 더하면 평형상수 K = K1 × K2가 됨
③ 규칙 3. 평형상수가 K1인 반응식에서 K2인 반응식을 빼면 평형상수 K = K1 ÷ K2가 됨
⑺ 평형상수 K에 따른 반응의 정도 예측
① K > 103 : 생성물이 dominant
② K = 10-3 ~ 103 : 어느 것도 dominant하지 않음
③ K < 10-3 : 반응물이 dominant
2. 르 샤틀리에 원리(principle of Le Chatelier) [목차]
⑴ 정의 : 계에 변화를 주었을 때 변화를 최소화하는 방향으로 평형이 이동한다는 원리
⑵ 농도에 의한 평형 이동
① 물질을 첨가하면, 첨가한 물질이 감소하는 방향으로 평형 이동
② 반응과 무관한 물질이 첨가되면 평형 이동은 없음
⑶ 부피에 의한 평형 이동
① 기체의 부피가 커지면 기체의 분자수가 증가하는 방향으로 평형 이동
○ (주석) 자연은 변화를 싫어하지만 이 경우 변화를 증폭한다는 점에서 유의
② 기체의 압력이 커지면 기체의 분자수가 감소되는 방향으로 평형 이동
③ 용액의 부피가 커지면 입자의 수가 증가하는 방향으로 평형 이동
④ 비활성기체의 첨가 효과
○ 일정 부피 조건 : 평형이동이 없음
○ 일정 압력 조건 : 비활성기체에 의해 부피가 증가하므로 기체 분자수가 증가하는 방향으로 평형이동
⑷ 온도에 의한 평형 이동
① 계의 온도가 높아지면 흡열반응이 우세
② 계의 온도가 높아지면 발열반응의 평형상수는 감소하고, 흡열반응의 평형상수는 증가
③ (참고) 온도가 증가하면 활성화에너지를 넘는 분자들이 많아져 정반응, 역반응 모두 증가
3. 고난이도 문제 유형 : 기체 + 화학평형 [목차]
⑴ 어려운 이유
① 평형상수 계산 시 압력을 쓰지만, 화학반응 자체는 몰수로 고려해야 하므로, 계산량이 많아짐
② 팁 : 무조건 압력으로만 문제를 풀자.
⑵ 초기 상태
① ⑶ ~ ⑸에 근거하여 계산
② 온도가 변하는 경우 : 평형 상수가 변하므로 주어진 계의 상태를 초기상태로 보고 계산
⑶ 부피가 고정 장치로 고정된 경우

① A, B, C의 초기 압력을 PA0, PB0, PC0라고 정의
② 압력비가 곧 몰수비이므로 최종 압력을 다음과 같이 표시할 수 있음
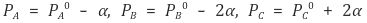
③ 주어진 평형상수에 맞춰 α를 구할 수 있음
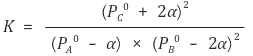
⑷ 전체 압력이 일정한 경우

① A, B, C의 초기 압력을 PA0, PB0, PC0라고 정의
② 먼저 화학반응을 하고 이상기체 상태방정식을 맞춰도 최종 상태는 동일
③ 화학반응의 몰수비를 먼저 고려하는 의미에서 A, B, C의 나중 압력을 다음과 같이 표시할 수 있음
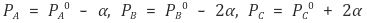
④ 이상기체 상태방정식을 고려하면 A, B, C의 최종 압력을 다음과 같이 표시할 수 있음
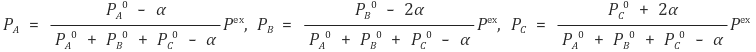
⑤ 주어진 평형상수에 맞춰 α를 구할 수 있음
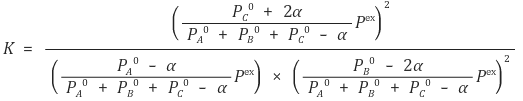
⑸ 최종 부피가 일정한 경우

① 대부분 최종 압력 Pf = β인지 물어보는 경우가 거의 대부분
② 먼저 이상기체 상태방정식을 통해 최종 압력을 추정
○ nf 계산
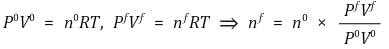
○ α 계산
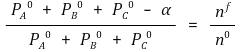
○ 각 압력 계산

③ 주어진 평형상수에 대입해서 Pf = β라는 가정이 타당한지 확인
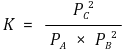
입력: 2019.01.01 11:53
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 19강. 용해도와 착이온 평형 (0) | 2018.12.27 |
|---|---|
| 【화학】 18강. 산·염기 반응 (16) | 2018.12.27 |
| 【화학】 15강. 전기화학 (48) | 2018.12.27 |
| 【화학】 14강. 산화환원반응 (0) | 2018.12.27 |
| 【화학】 13-1강. 열역학 과정과 카르노 순환 (8) | 2018.12.27 |



최근댓글