14강. 교류회로이론(frequency-domain)
추천글 : 【회로이론】 회로이론 목차
1. 개요 [목차]
⑴ 교류의 장점
① 전압 변환 용이
② 장거리 전송 효율 우수 (∵ 고전압)
⑵ 평균값과 실효값
① 평균값 : 주기함수의 평균값은 0이므로 절대값의 평균을 고려

② 실효값 : 교류전원과 같은 효과(주로 전력)를 내는 직류전원 값

⑶ 일반적인 교류 회로는 단일 주파수를 가지는 정현파 전원을 가지고 있음
① 반례 : 비정현파
⑷ 교류회로와 직류회로 공통
① 직렬-병렬 합성
② 키르히호프 법칙
③ 중첩의 원리
④ 등가회로
3. 페이저의 개념 [목차]
⑴ 라플라스 변환 : 모든 시스템을 쉽게 해석할 수 있음
① 1st. 순시전압, 순시전류, 순시전력 등에 대한 문제는 라플라스 변환인 V, I, P등에 대한 표현으로 변환
○ 순시전압 : 특정 순간에 측정된 전압. v(t)로 표시
○ 순시전류 : 특정 순간에 측정된 전류. i(t)로 표시
○ 순시전력 : 특정 순간에 측정된 전압과 전류의 곱. p(t)로 표시
② 2nd. V, I, P 등의 해를 각각 구함
③ 3rd. V, I, P의 라플라스 역변환인 v(t), i(t), p(t)를 구해 원하는 형태의 해를 구함
④ 4th. s가 포함된 식은 라플라스 변환식 ↔ jω가 포함된 식은 페이저 식
○ 저항의 단자 특성
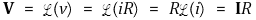
○ 캐패시터의 단자 특성
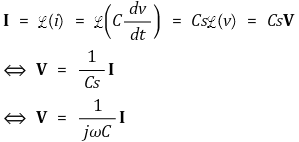
○ 인덕터의 단자 특성
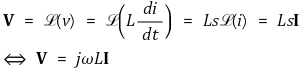
⑵ 페이저(복소형식, phasor) : 정상 정현파량을 복소량으로 표시한 것
① 도입 : 복소수는 복소평면(complex plane)이라는 강력한 비주얼라이징 툴이 존재함
② 전제 : v(t) = A cos(ωt + θ)에 대해,
○ 이를 페이저라는 복소수의 실수부로 간주
○ ωt는 공통이므로 무시
③ 복소량의 표현
○ 직각좌표계 : z = x + jy
○ 극좌표계 : z = r∠θ○ 원의 방정식 : z = rejθ
④ 페이저의 연산

⑶ 라플라스 변환은 모든 시스템에 적용할 수 있으나 페이저는 교류 회로에서만 쓸 수 있음
① 복소형식은 안 되고 라플라스 변환만 적용 가능한 예가 있음
② 예 : 직류전압과 교류전압이 동시에 쓰이는 전자기파 발진회로
4. 페이저의 응용 [목차]
⑴ 임피던스(impedence, Z로 표시)
① 개요
○ 복소형식에서 저항, 커패시터, 인덕터를 저항처럼 간주할 수 있음
○ 중요한 이유 : 미분연산을 사칙연산으로 대체할 수 있음
② 저항 : R (Ω)만큼의 임피던스를 가짐
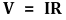
③ 캐패시터 : 1/jωC (Ω)만큼의 임피던스를 가짐
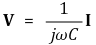
④ 인덕터 : jωL (Ω)만큼의 임피던스를 가짐
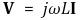
⑤ 임피던스 = 저항 + j × 리액턴스
○ 저항 : 임피던스의 실수부
○ 리액턴스(reactance) : 임피던스의 허수부. X로 표시. 커패시터와 코일의 공진 반응(reaction)에서 유래
○ 어드미턴스(admittance) : 임피던스의 역수
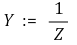
○ 어드미턴스 = 컨덕턴스 + j × 서셉턴스
○ 컨덕턴스(conductance) : 어드미턴스의 실수부
○ 서셉턴스(susceptance) : 어드미턴스의 허수부
⑥ 복소형식임을 전제한 교류 회로에서 j 값을 생략하여 표현하는 경우도 있음
⑵ 복소형식에서도 직류회로이론이 여전히 성립
① 예제 1. node voltage analysis
Figure. 1. node voltage analysis 예제
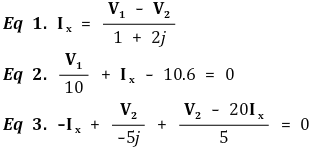
② 예제 2. mesh current analysis
Figure. 2. mesh current analysis 예제
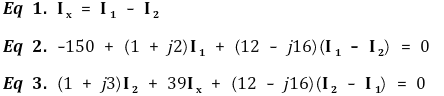
⑶ 위상자도(페이저도, phasor diagram)
① 정의 : 전압, 전류, 전력 등을 복소평면상에 나타낸 그래프
○ 초록색 화살표가 빨간색 화살표보다 빠름 (위상차가 180도 미만이 되도록 한 뒤 속도 비교 가능)
Figure. 3. 위상자도
○ 위상자도에서 ωt의 위상을 0°로 가리킴○ 예 : I = 50 sin(ωt + ∠0) → I = 50 ∠0
② 지상전류(lagging current) : 인덕터
○ 인덕터(코일)를 유도 임피던스, 유도 리액턴스라고도 부름
○ 지상전류 페이저도
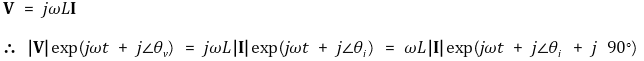
③ 진상전류(leading current) : 캐패시터
○ 커패시터를 용량 임피던스, 용량 리액턴스라고도 부름
○ 진상전류 페이저도
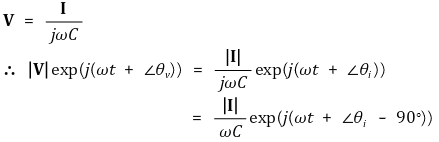
5. 전력 [목차]
⑴ 개요
① 전력은 직류회로이론 때도 그랬던 것처럼 단순하지 않은 제어량임
② 에너지 보존법칙에 의해 회로 내 모든 소자의 전력의 합은 0이다.
⑵ RMS (root-mean-square; 제곱 평균 제곱근) : RMS를 도입하는 이유는 직류회로와의 유사성 때문
① RMS 전압
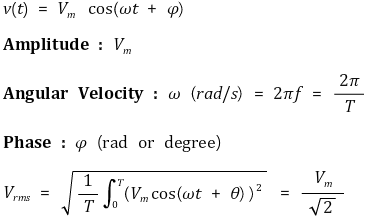
○ 대한민국 기준
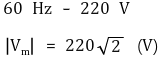
② RMS 전류
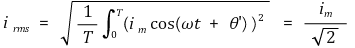
③ 실효값 : RMS 정의에 따라 산출된 물리량
○ 도입 배경 : 전력 = 전압 × 전류의 형태가 자연스럽기 때문에 전압 및 전류의 대표값으로 실효값을 정의
○ 정현파 전압 및 전류를 복소평면상에 화살표로 표시하는 페이저(phasor)에서 일반적으로 실효값 사용
○ 파형률 = 실효값 / 평균값 ○ 파고율 = 최대값 / 실효값
④ 저항, 코일, 커패시터의 전력
○ 저항에서 사용하는 에너지
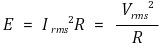
○ 코일에 저장된 에너지
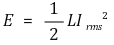
○ 커패시터에 저장된 에너지
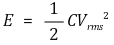
⑶ 전력 계산
① 시간 도메인(time-domain) 전력 계산
○ 우선 v와 i가 다음과 같이 표현된다고 가정 : Vm = Vpeak = 최댓값
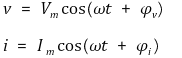
○ 그럼 전력의 기대값은 다음과 같다.
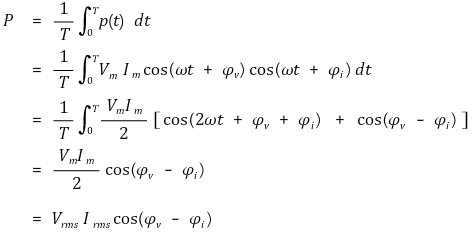
② 피상전력(apparent power)
○ 정의 : 허수 값까지 고려한 전력값. 전압 페이저와 전류 페이저를 곱한 것
○ 단위 : VA(voltage-ampere)
○ 수식화
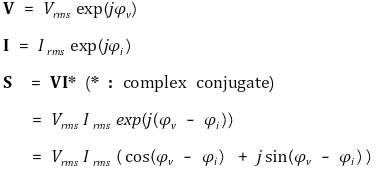
○ 켤레복소수(complex conjugate)를 곱하는 이유
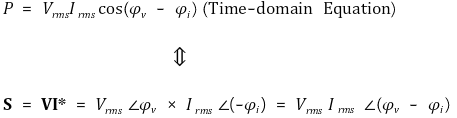
○ 켤레복소수를 취하는 게 전압이어도 되고, 전류여도 됨
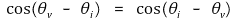
③ 유효전력(active power)
○ 실제로 저항에 의해서 쓰이는 전력(P)
○ 단위 : W(Watt)
○ 유효전력은 저항에서의 전력과 필요충분조건

④ 무효전력(reactive power)
○ 코일, 커패시터에 저장되는 전력으로 Q를 의미
○ 단위 : VAR(volt-ampere reactive)
○ 수식화
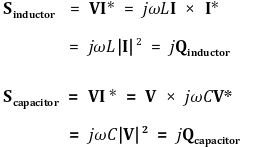
○ 코일, 커패시터에 머무는 에너지는 실제로 아무 일도 하지 않음
○ 무효전력은 전자가 회로를 돌면서 자기가 가진 에너지를 전부 쓰지 않고 전원으로 돌아오는 양
○ 인덕터의 무효전력이 양의 값 : 전기 에너지가 자기장 에너지로 전환
○ 인덕터의 무효전력이 음의 값 : 자기장 에너지가 전기 에너지로 전환
○ 무효전력은 유효전력을 높임
○ 리액턴스는 무효전력을 발생시켜 역률을 낮춤
○ 역률을 낮추면 같은 일을 하기 위해 더 많은 전류가 흘러야 함
○ 더 많은 전류가 흐르면 저항을 통해 손실되는 에너지(유효전력) 또한 커짐
⑤ 역률(power factor) : cos θ (단, θ : 전류와 전압의 위상차)로 나타남
○ 빗변의 길이 × cos θ = 밑변의 길이
○ 복소수의 크기 × cos θ = 실수값
○ 피상값의 크기 × cos θ = 유효값
○ |유효전력| ÷ |피상전력| = cos(θv - θi)
○ (참고) 무효도 : |무효전력| ÷ |피상전력| = sin(θv - θi)
○ 회로상에서 음의 저항은 존재하지 않으므로 cos(θv - θi)가 음이 될 일은 없다.
○ 표시 : lagging/leading p. f
⑷ 부하 임피던스와 최대 유효전력
Figure. 6. 부하 임피던스와 최대 유효전력
(단, VS는 rms 전력으로 표기돼 있음)
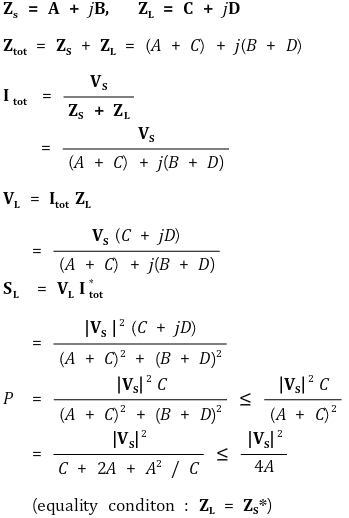
⑸ phase compensation
(단, VS는 rms 전력으로 표기돼 있음)
① 계산
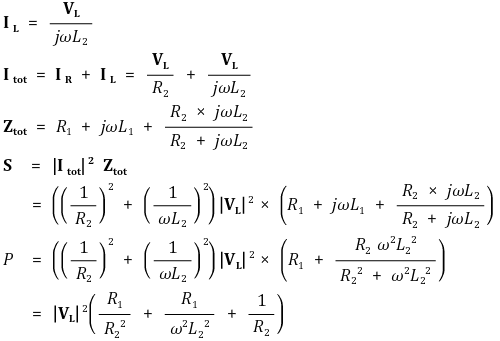
○ VL은 일정 : 수용가의 전압값이 일정하도록 전원의 전압이 계속 피드백을 받음
○ P는 L2에 대한 감소함수 : L2가 ∞가 되는 것(⇔ 부하 코일의 효과를 없애는 것)이 가장 효율적임
② 커패시터 도입 : 공진을 통해 부하 코일의 효과를 없앨 수 있음
Figure. 8. phase compensation에서 커패시터를 도입한 것
③ (참고) 공진현상
○ 공진(resonance) : 용량 리액턴스와 유도 리액턴스가 서로 상쇄되어 무효전력이 0이 되는 현상
○ RLC 직렬
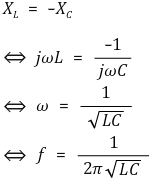
○ RLC 병렬
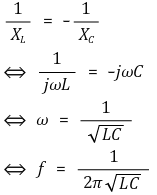
⑹ 예제 1. 저항 부하는 순저항만 있고 50 kW를 소모한다. 모터의 피상전력 크기는 100 kVA이고, 역률이 0.8 lagging p. f 이다.
Figure. 9. 예제 1
(단, VS는 rms 전력으로 표기돼 있음)
① 저항부하와 모터에 흐르는 각 전류와 Itot을 구하라.

② 모터와 부하저항을 병렬로 연결한 부하의 피상전력과 역률을 구하여라.
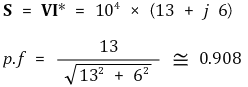
6. 비정현파 [목차]
⑴ 개요
① 일정한 주기를 갖는 모든 파형은 정현파의 합으로 나타낼 수 있음
② 이 정현파들은 기본파와 기본파의 정수배 주파수를 갖는 고조파로 나눌 수 있음
③ 푸리에 급수 표현

⑵ 해석
① 중첩의 원리로 해석
② 주파수에 따라 임피던스가 달라지는 것에 유의
⑶ 전압
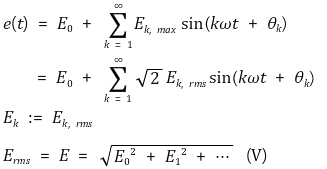
⑷ 피상전력(apparent power)
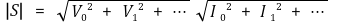
⑸ 역률
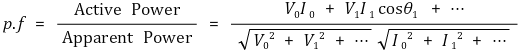
7. 변압기(transformer) [목차]
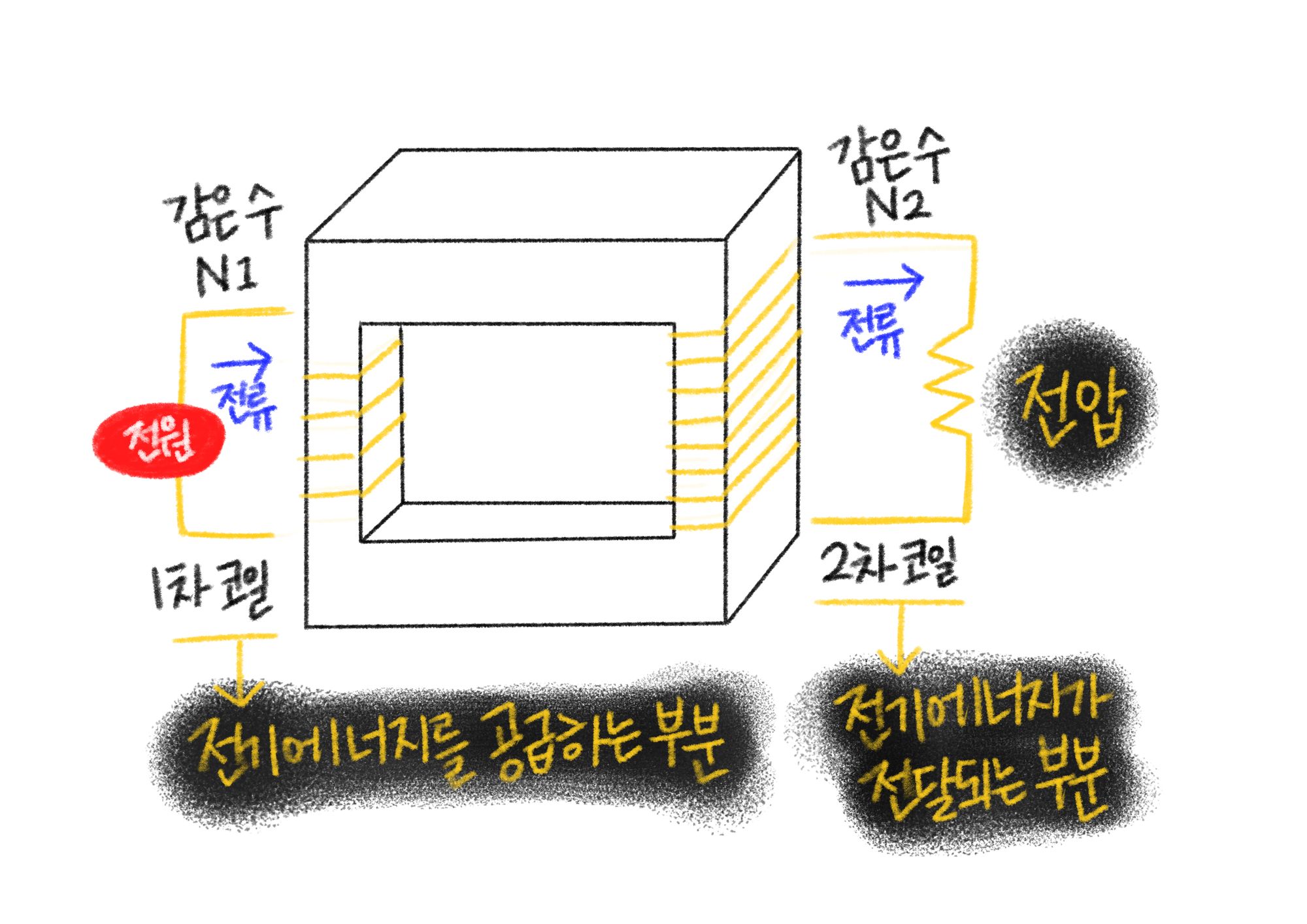
⑴ 구조 : 얇은 금속판 여러 장을 붙인 回 모양의 철심 양쪽에 코일을 감은 구조
Figure. 10. 변압기의 구조
⑵ 기능
① 임피던스 정합
② 부하로 교류를 통과시키는 반면 직류는 격리
③ 균형회로(balanced circuit)와 불균형회로(unbalanced circuit), 급전시스템(feed system), 부하(load)를 조화롭게 연결
④ 변압기에서 전력은 보존
⑶ 변압기 철심이 갖추어야 할 조건
① 투자율이 클 것
② 전기저항이 클 것
③ 성층 철심으로 할 것
④ 히스테리시스손 계수가 작을 것
⑷ 상호유도(Mutual Inductance)
① 상호유도계수 도입
○ 상황 : n개의 코일이 있고, 각 코일에 전류 ip가 흐름
○ ΦB, p, q : q번째 코일에만 전류 iq가 흐를 때 p번째 코일 단자에 생기는 자속
○ 맥스웰 법칙에 의해 다음과 같은 상수를 찾을 수 있음
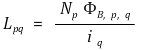
○ p = q인 경우 : Lpq를 self-Inductance라고 부름. 그 도체에 의해 생기는 인덕턴스
○ p ≠ q인 경우 : Lpq를 mutual-Inductance라고 부름. 다른 도체에 의해 생기는 인덕턴스
○ p번째 도체에 생기는 총 자속 : Faraday's law를 적용할 수 있음
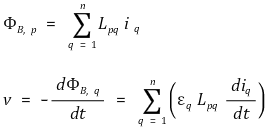
○ εq : 어떤 방향을 전류의 + 방향으로 했는지에 따라 -1 또는 1이 되는 상수
○ 두 개의 코일의 경우
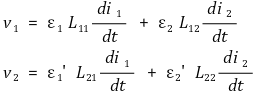
⑸ dot convention : 점이 찍혀 있는 방향으로 전류가 증가하면 자속이 더해진다고 약속
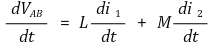
① VAB = VA - VB를 의미
② i1 : A에서 B로 흐르는 전류
③ i2 : D에서 C로 흐르는 전류
⑹ 변압기 해석
Figure. 12. 변압기 해석
① 1단계. M12 = M21
○ 상황 : 어떤 도체의 서로 다른 부분에 두 코일이 감겨져 있음
○ i1 : 코일 1에 흘린 전류
○ Φ1 : 코일 1과 쇄교하는 전 자속
○ Φ1 = Φ11 + Φ12
○ Φ11 : 코일 1의 전류에 의해 코일 1만 통과하는 누설자속
○ Φ12 : 코일 1의 전류에 의해 코일 2를 통과하는 자속
○ i2 : 코일 2에 흘린 전류
○ Φ2 : 코일 2와 쇄교하는 전 자속
○ Φ2 = Φ21 + Φ22
○ Φ21 : 코일 2의 전류에 의해 코일 1을 통과하는 자속
○ Φ22 : 코일 2의 전류에 의해 코일 2만 통과하는 누설자속
○ 맥스웰 법칙 : Φ ∝ 1/N, Φ ∝ I → L 도출
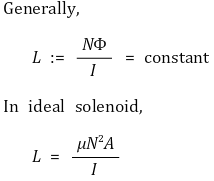
○ 대칭성을 이용하여 최종 결론을 보일 수 있음
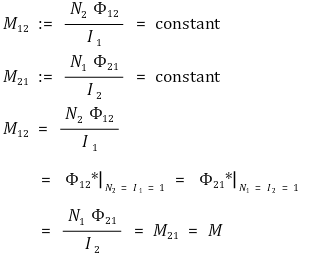
② 2단계. M = √(L1L2)
○ 결합계수(coupling factor) : 두 코일 간의 유도결합 정도를 나타내는 양
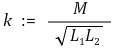
○ k = 0 : 상호자속이 없는 경우 (무유도결합 상태)
○ k = 1 : 누설자속이 없는 경우 (완전유도결합 상태)
○ 코일이 이상적인 솔레노이드인 경우 k = 1
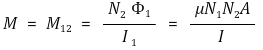
③ 3단계. V2 = aV1
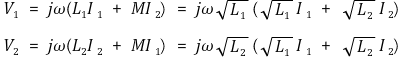
○ L ∝ N2이므로 준명제를 증명
○ 변압기가 순접이 아니라 역접이어도 똑같은 결론이 나옴
④ 4단계. KVL(Kirchhoff's Voltage Law) 식을 적용하자.
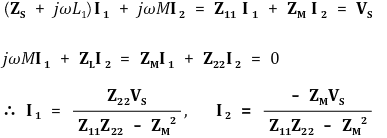
○ 만약 전원측 부하 ZS = 0이라면 | I1 | = a | I2 |가 성립 : 이 경우, P = V1I1 = V2I2 라서 전력이 보존됨을 쉽게 보일 수 있음
○ 다음과 같은 합성 임피던스를 발견할 수 있음
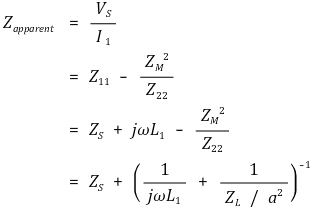
○ 변압기를 a2만큼 크기가 작아진 부하 임피던스와 1차 회로의 코일의 병렬연결로 간주할 수 있음
○ 코일 자체도 또한 저항이 있으므로 합성 임피던스가 다음과 같이 수정돼야 함
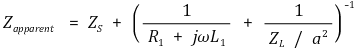
○ 변압기 철심은 저항이 크므로 합성 임피던스는 다음과 같이 근사될 수 있음
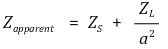
○ 이상적인 변압기 회로에서 최대전력이 전달되는 조건은 다음과 같음
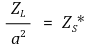
⑤ 5단계. 실제 피상전력과 합성 임피던스의 피상전력은 같다.
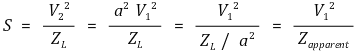
⑺ 임피던스 정합(Impedance Matching) 예제 : 부하에 최대전력이 전달되도록 설계하라.
① 1단계. 입력 임피던스는 1 + j 2π ⅹ 10-1 Ω이다.
② 2단계. 부하 임피던스가 1 - j 2π ⅹ 10-1 Ω인 경우 최대 전력이 전달된다.
③ 3단계. 감은 수의 비가 1 : 10인 변압기로 저항의 값을 맞춘다.
Figure. 14. 임피던스 정합 3단계
④ 4단계. 커패시터를 삽입하여 허수부의 값을 조절
Figure. 15. 임피던스 정합 4단계
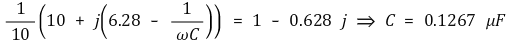
⑻ 캠벨 브릿지(Campbell bridge)
① 캠벨 브릿지 해석
② 평형 조건 : 2차 회로의 전류가 0이 되는 조건
⑼ 변압기의 %임피던스
① 변압기의 임피던스 전압 : 변압기의 임피던스와 정격 전류와의 곱
② %저항 강하
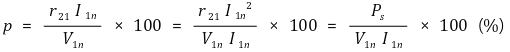
③ %리액턴스 강하
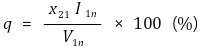
④ %임피던스 강하
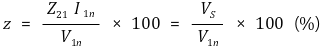
⑤ 동손(임피던스 와트)
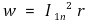
⑽ 응용
① 응용 1. 변전소 변압기
② 응용 2. 납땜인두, 글루건
○ 출력측 전압이 입력측 전압보다 n배 감소하면 출력측 전류는 대략 n배 증가함
○ 부하열은 전류의 제곱에 비례하기 때문에 이 변압기 회로는 n2배의 열량을 낼 수 있음
○ 실제로 납땜인두, 글루건은 출력열을 극대화하기 위해 출력측 코일의 감은 횟수를 1로 함
③ 응용 3. 휴대전화의 무선충전
○ 1st. 무선 충전기에서 윗방향으로 증가하는 자기장이 발생
○ 2nd. 휴대전화 내부 코일에 자기 선속이 증가
○ 3rd. 휴대전화 내부 코일에서 자기 선속의 증가를 방해하는 방향으로 유도기전력 및 유도전류 발생
○ 4th. a 방향으로 전류 발생
○ 5th. 휴대전화 내부의 커패시터에 전하가 저장됨 (충전)
④ 응용 4. 인덕션 레인지
○ 1st. 인덕션 레인지 내부 코일에 전류가 흐름 : 20000 Hz 이상의 교류가 흐름
○ 2nd. 조리 기구가 2차 코일의 역할을 하여 조리 기구에 유도 전류가 발생
○ 3rd. 이 전류에 의해 조리 기구가 가열됨
○ 3-1. 유전가열
○ 대상 : 목재, 고무, 면 등의 유전체
○ 원리 : 유전체손에 의한 자기 발열
○ 특징 : 피가열물의 내부로부터 균일하게 가열
○ 3-2. 유도가열
○ 대상 : 금속류
○ 원리 : 피가열물에 유기되는 와전류에 의한 줄열
⑤ 응용 5. 교통카드 단말기
○ 1st. 교통카드를 교류가 흐르는 단말기에 접촉
○ 2nd. 교통카드 내부의 코일을 통과하는 자기장이 변하여 고통카드에 유도 전류가 흐름
⑥ 응용 6. 금속 탐지기
○ 1st. 금속 탐지기의 전송 코일에 교류가 흐름
○ 2nd. 전자기 유도에 의해 금속에도 전류가 흐름
○ 3rd. 금속 물질에서 발생되는 자기장의 변화를 검출 코일이 감지함
⑦ 응용 7. 고압 방전 장치 : 자동차의 연료에 불을 붙이는 데 이용됨
○ 1st. 1차 코일에 전류를 흐르게 하다가 갑자기 끊음
○ 2nd. 2차 코일에 과전류가 유도됨
○ 3rd. 2차 코일에 연결된 두 금속 사이에서 불꽃이 튐
입력: 2016.01.20 23:54
수정: 2018.12.12 11:56
'▶ 자연과학 > ▷ 회로이론' 카테고리의 다른 글
| 【회로이론】 16강. 4단자망과 제어이론 (0) | 2016.06.27 |
|---|---|
| 【회로이론】 회로이론 응용: Flash Lamp (4) | 2016.06.27 |
| 【회로이론】 회로이론 응용 : 스피커 (0) | 2016.06.27 |
| 【회로이론】 6-16강. 등가회로의 존재성 반증 (0) | 2016.06.27 |
| 【회로이론】 6-15강. RLC 복합회로 (0) | 2016.06.27 |






















최근댓글