15강. 다층퍼셉트론(MLP, multilayer perceptron)
추천글 : 【알고리즘】 알고리즘 목차
1. 보편근사이론(universal approximation theorem) [목차]
⑴ Cybenko (1989)와 Hornik (1991)이 제안
⑵ 내용
① Hornik (1991)은 유계이고 정규화된 어떤 함수 f : ℝd → ℝ도 한 개의 은닉층이 있고, 같은 활성화 함수를 가지며, 한 개의 선형 출력 뉴런을 가지는 유한한 크기의 신경망으로 표현될 수 있음 (ref)
② 𝜙가 유계이고, 연속이며 단조증가하는 활성화 함수라고 하자. 또한 𝐾𝑑를 ℝ𝑑의 부분집합이고 컴팩트한 집합이라고 하고, 𝐶(𝐾𝑑)를 𝐾𝑑의 부분집합이고 연속인 함수라고 하자. 이때 모든 𝜖 > 0에 대하여 어떤 𝑁 ∈ ℕ, 실수 𝑣𝑖, 𝑏𝑖, ℝ𝑑, 벡터 𝜔𝑖가 있어서, 만일 다음과 같이 정의하면,
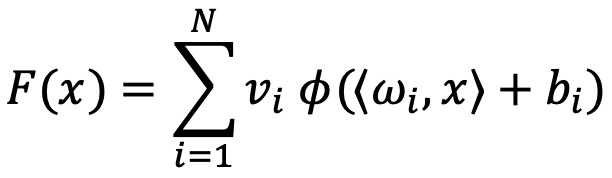
다음을 얻는다.

③ 시그모이드 활성화 함수를 가지는 특수한 케이스에 대한 보편 근사 이론은 이미 Cybenko (1989)에 의해 증명
⑶ 한계
① 이 이론은 이론적인 면에서는 흥미롭지만 한 개의 은닉층으로 구현하려면 은닉층에 있는 뉴런의 수가 매우 많아질 것이므로 실질적으로 그렇게 유용하지 않음 : 딥러닝의 효과는 깊음, 즉 은닉층의 수에 있음
2. 다중 퍼셉트론 알고리즘(MLP, multi-layer perceptron) [목차]
⑴ 개요
① 여기서는 한 개의 입력층, 은닉층, 출력층으로 이루어진 삼중 퍼셉트론에 대해서 다루도록 함
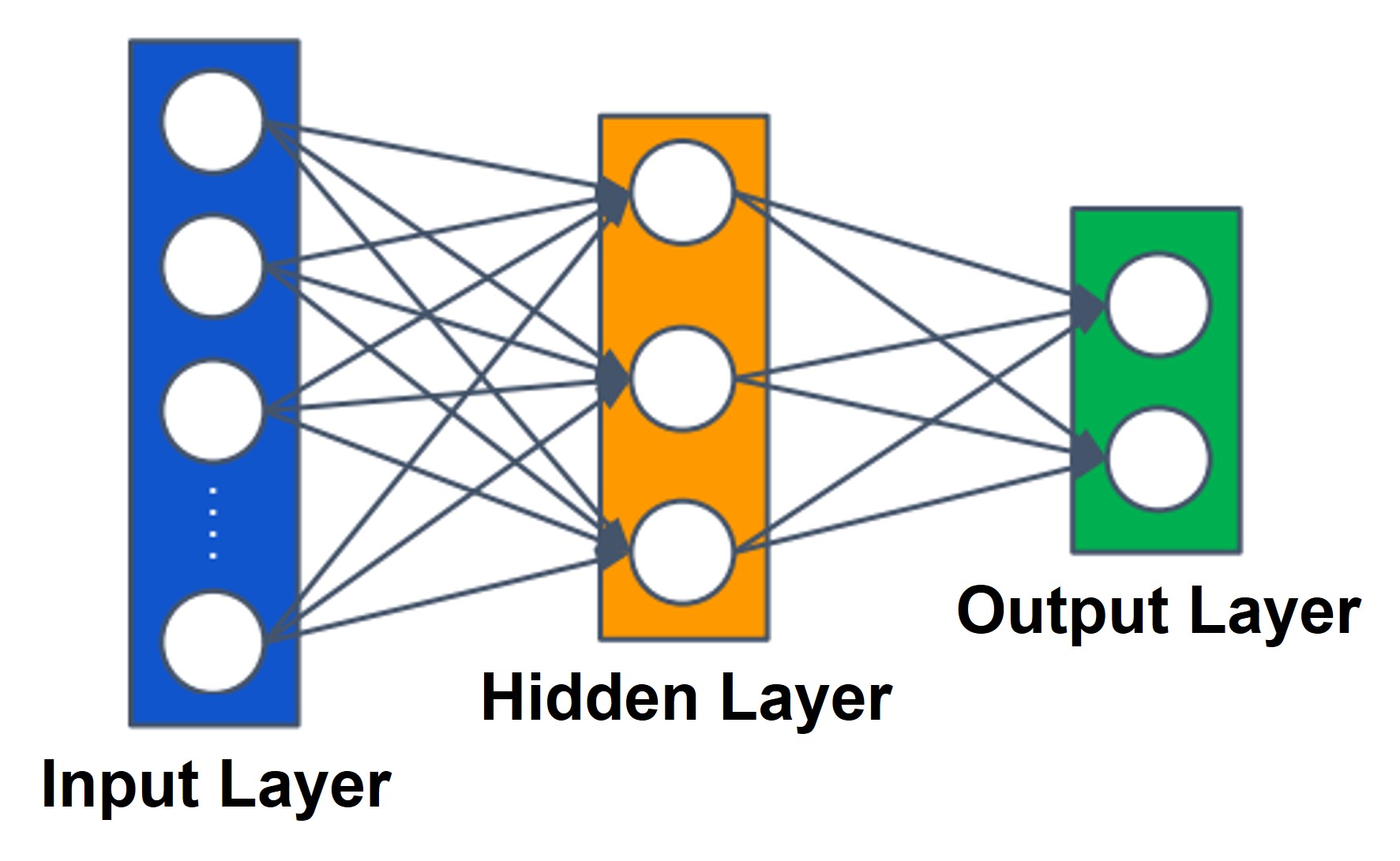
Figure. 1. 2층 퍼셉트론
○ 입력층(input layer) : 일반적으로 입력층은 퍼셉트론의 층수에 포함시키지 않음
○ 은닉층(hidden layer)
○ 출력층(output layer)
② 파라미터 정의
○ L : 입력층 뉴런의 개수
○ M : 은닉층 뉴런의 개수. 초매개변수(hyperparameter)로 설정 가능
○ N : 출력층 뉴런의 개수
○ i : 입력층 뉴런을 표현하기 위한 반복변수
○ j : 은닉층 뉴런을 표현하기 위한 반복변수
○ k : 출력층 뉴런을 표현하기 위한 반복변수
○ xι : ι번째 입력층 뉴런의 노드값. 즉 입력값
○ x0 : -1로 정의
○ hζ : ζ번째 은닉층 뉴런의 시냅스합, 혼동을 피하기 위해 hζhidden라고도 표현함
○ aζ : ζ번째 은닉층 뉴런의 노드값. 1보다 작아야 함
○ a0 : -1로 정의
○ hκ : κ번째 출력층 뉴런의 시냅스합, 혼동을 피하기 위해 hκoutput라고도 표현함
○ yκ : κ번째 출력층 뉴런의 노드값. 즉 출력값. 1보다 작아야 함
○ tκ : κ번째 출력층 뉴런의 목표값. 즉 학습 데이터로 제공되는 값
○ v0ζ : hζ에 적용되는 바이어스 (bias)
○ vιζ : ι번째 입력층 뉴런과 ζ번째 은닉층 뉴런 간 시냅스의 가중치
○ ω0κ : hκ에 적용되는 바이어스
○ ωζκ : ζ번째 은닉층 뉴런과 κ번째 출력층 뉴런 간 시냅스의 가중치
○ v : 모든 vιζ를 포함하는 행렬
○ w : 모든 ωζκ를 포함하는 행렬
○ δh(ζ) : ζ번째 은닉층 뉴런의 에러값
○ δo(κ) : κ번째 출력층 뉴런의 에러값
○ g(·) : 활성화 함수
③ 여기서 노드값은 시냅스합을 활성화 함수로 적용한 결과임을 주의
④ 바이어스의 의미 : 개별 데이터셋과 무관하게 클래스 자체의 패턴을 반영
⑵ 활성화 함수(activation function)
① 항등함수(identity) = x : 이 형태를 linear classifier라고 함
② sigmoid σ(x) = 1 / (1 + e-σx)
○ 미분가능하며 함숫값이 [0, 1]에 머물기 때문에 전통적으로 가장 많이 사용되는 활성화 함수
○ 생물학 실험 데이터가 이와 유사함
○ 포화선(saturation curve)을 σ로 조절할 수 있음
○ σ → ∞으로 발산하면 hard limiter가 됨
○ x의 절댓값이 커지면 그 기울기가 0에 매우 가까워지는 점은 모델의 학습력을 떨어트려 문제가 됨
③ tanh(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
④ arctan(x)
⑤ 강한 역치 함수 : φβ(x) = 1x ≥ β
⑥ ReLU (rectified linear unit) : max(0, x). 가장 자주 사용됨
⑦ leaky ReLU : max(0.1x, x)
⑧ maxout : max(w1Tx + b1, w2Tx + b2)
⑨ elu (exponential linear unit) : x if x ≥ 0; α(ex - 1) if x < 0
⑩ softmax
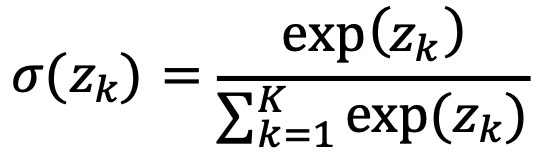
⑶ 손실 함수(loss function) : 에러 함수(error function), 비용 함수(cost function)라고도 함
① 정의 : 현재 학습된 모델의 예측이 얼마나 맞았는지를 수치화한 것
② 방법 1. L2 손실함수 : 이후의 과정은 방법 1을 기준으로 함
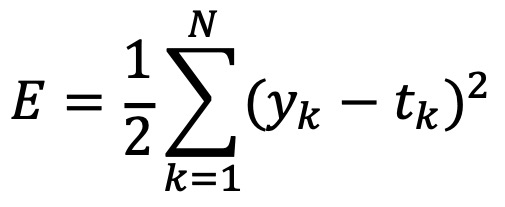
○ 출력값과 목표값의 차이를 제곱하고 이것들의 합 E를 에러 함수로 사용해서 에러를 계산하도록 함
○ 이때 계수 1/2은 미분할 때 편의성을 제공하기 위함 : 1/2을 곱하는 게 의무사항은 아님
○ 위와 같이 합의 형태가 아니라 평균의 형태로 손실함수를 정의하기도 함 : 즉, E/N를 고려함
○ 따라서 에러 함수는 다음과 같이 표현할 수 있음
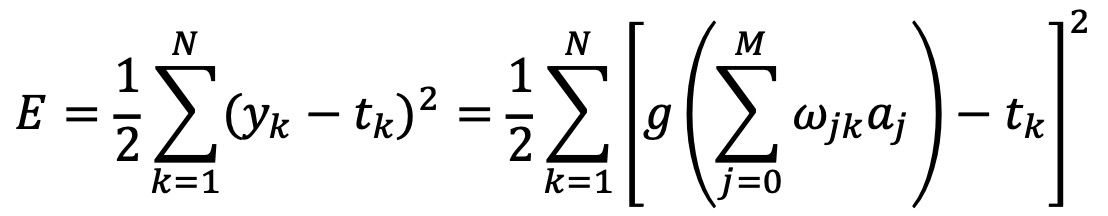
③ (참고) 방법 2. L1 손실함수
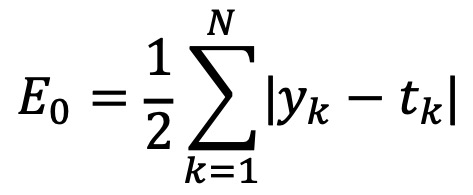
○ 출력값과 목표값의 크기에 따라서 어떤 값은 음수를 출력하고, 또 어떤 값은 양수를 출력
○ 이것들이 다 상쇄되어 E0는 0에 가까워질 수 있는 문제점이 있음
④ (참고) 방법 3. cross entropy
○ 일반적인 정의
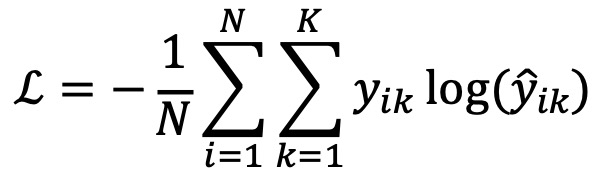
○ 이진 분류
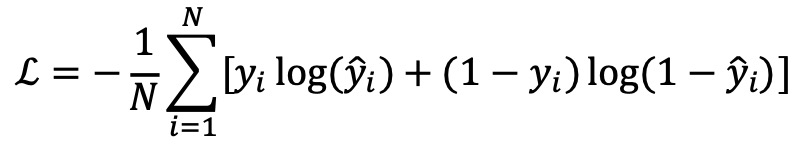
○ y가 one-hot vector [0, ···, 1, ···, 0]으로 표현된다면 다음과 같이 나타낼 수 있음
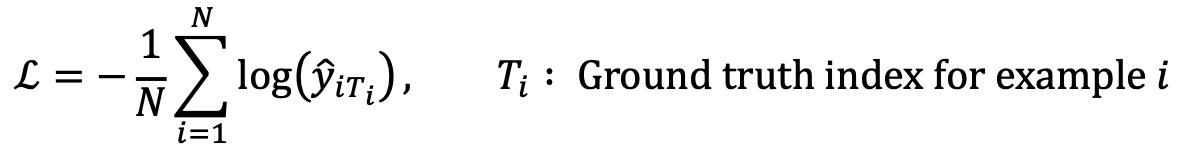
⑤ 방법 4. KLD(Kullback-Leibler divergence)
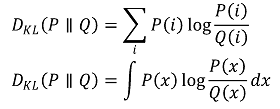
⑥ 방법 5. DT(Delaunay triangulation)
⑷ 역전파(backpropagation)
① 정의 : 기울기 하강 알고리즘(gradient descent algorithm)이 사용하기 위한 기울기를 계산하는 과정
② 예시 1
○ 단계 1. 고정된 ζ와 κ 값을 가진 상태에서 각 가중치 ωζκ를 조절하고, -E(w) 방향으로 갱신하는 알고리즘
○ 연쇄 법칙 (Chain Rule)을 적용한 결과와 hκ의 정의는 다음과 같음
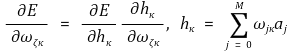
○ hκ의 정의를 이용하면 다음을 계산할 수 있음
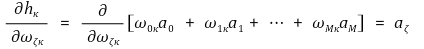
○ ∂E / ∂hκ 항은 에러 또는 변화량을 표현하는 항이어서 따로 생각할 만큼 중요함
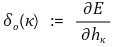
○ 여기서 연쇄 법칙을 사용한다면 이를 해결할 수 있음

○ 이때 출력층의 뉴런 κ의 출력값은 다음과 같음
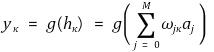
○ 여기서 g(·)는 활성화 함수로 시그모이드 함수를 포함해서 다양하게 선택할 수 있으므로 일반 함수로 생각
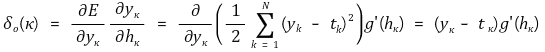
○ 따라서 출력층 가중치 ωζκ에 대한 갱신식은 다음과 같음
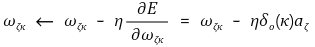
○ 단계 2. 고정된 ι와 ζ 값을 가진 상태에서 각 가중치 vιζ를 조절하고, -E(v) 방향으로 갱신하는 알고리즘
○ 연쇄 법칙을 적용한 결과와 hζ의 정의는 다음과 같음
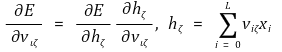
○ hζ의 정의를 이용하면 다음을 계산할 수 있음
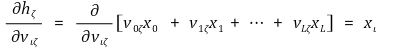
○ ∂E / ∂hζ 항도 따로 생각할 만큼 중요함
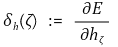
○ 여기서 연쇄 법칙을 사용한다면 이를 해결할 수 있음
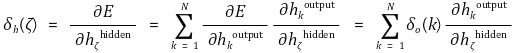
○ 그런데 시냅스합과 활성화 함수, 가중치의 정의에 따라 다음 식이 나옴
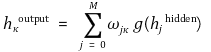
○ 이는 곧 다음을 의미함
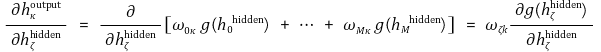
○ 이때 시그모이드 함수를 활성화 함수로 채택하면 위 식을 정리할 수 있음
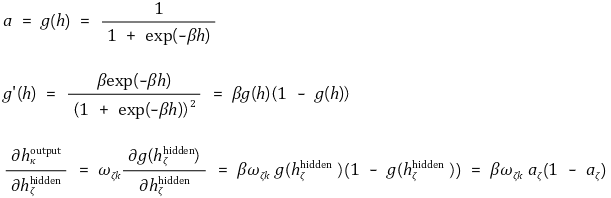
○ 따라서 다음과 같이 유도됨
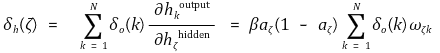
○ 그러므로 vιζ의 갱신 법칙은 다음과 같음
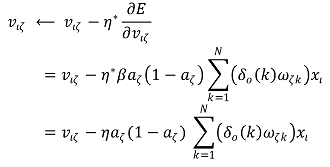
○ 단계 3. 입력과 출력들 사이에 더 많은 추가 은닉층이 존재한다면 똑같은 계산을 통해서 해결할 수 있음
○ 하지만 어떤 함수를 미분해야 하는지에 대해서 추적하기 점점 힘들어질 뿐임
③ 예시 2
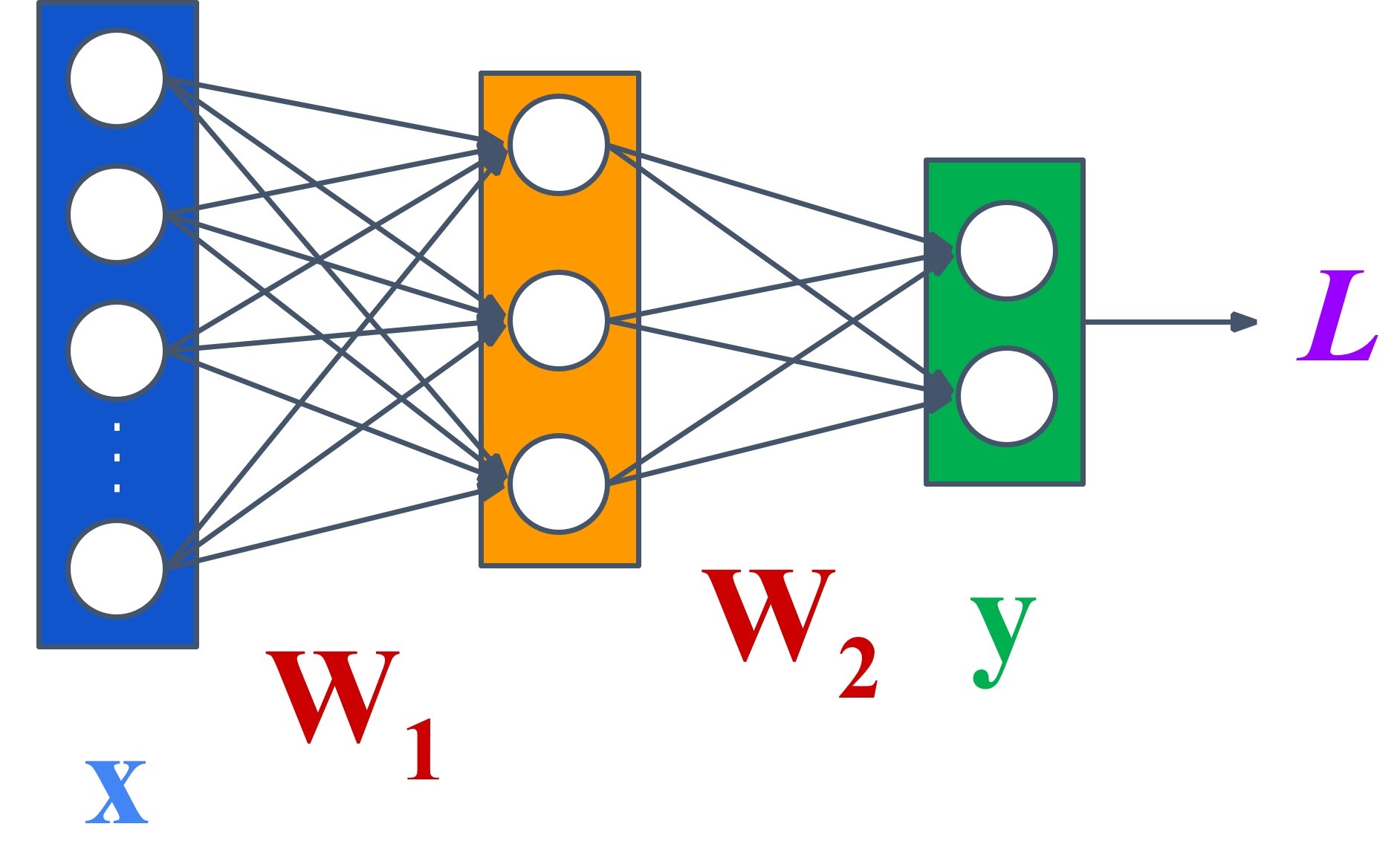
Figure. 2. 기울기 하강 알고리즘 예시

④ 예시 3
○ 개요
○ 복잡한 미분 전개를 필요로 하지 않음
○ 점화식처럼 하는 방식
○ 역전파 알고리즘의 반대는 순전파 알고리즘(feed-forward algorithm)
○ 방법
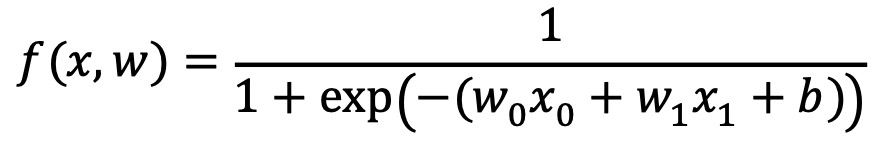
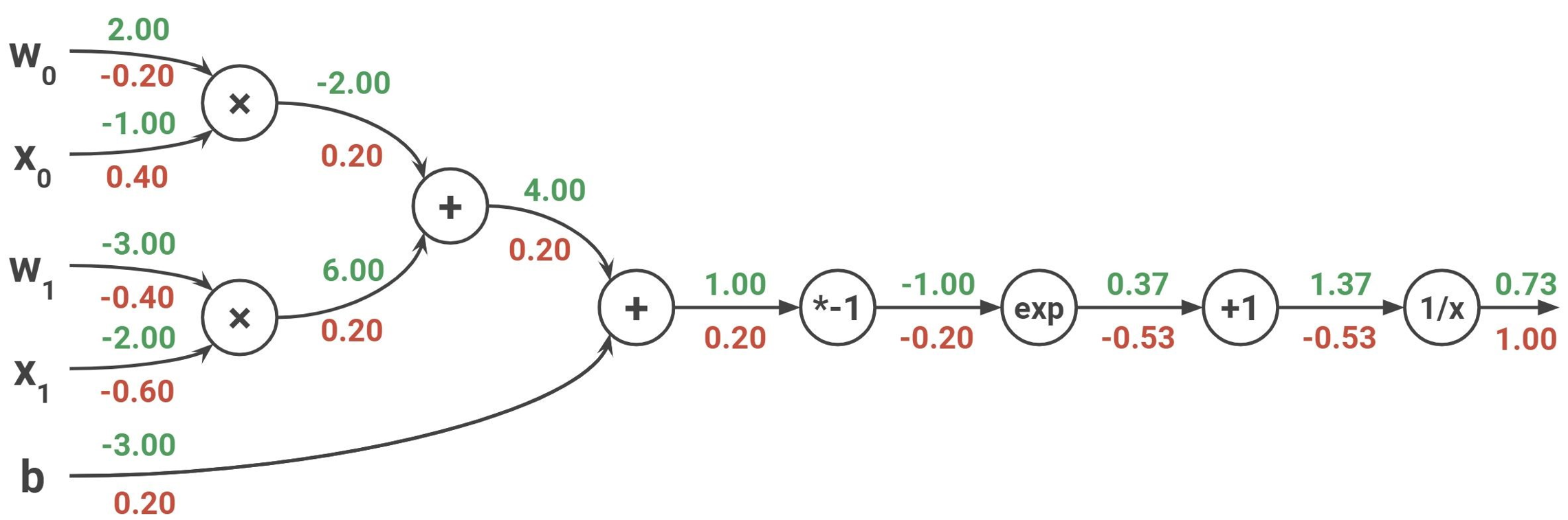
Figure. 3. backpropagation algorithm 예제
○ step 1. forward pass
○ step 2. 맨 끝의 upstream gradient는 1
○ step 3. local gradient를 계산 : 그 노드 자체에서 발생하는 그래디언트
○ step 4. downstream gradient를 계산 : upstream gradient × local gradient로 구함. 미적분의 chain rule에 근거함
○ step 5. gradient implementation
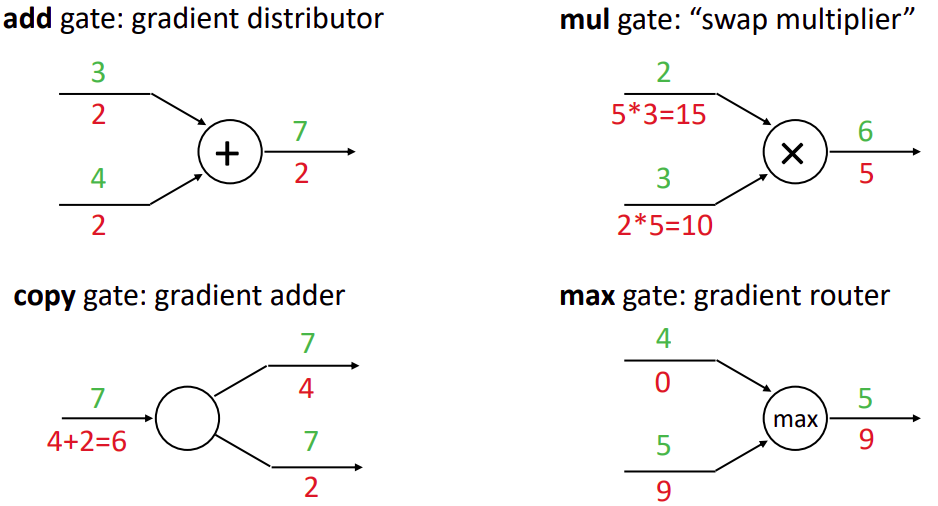
○ patterns in gradient flow
Figure. 4. patterns in gradient flow
○ add gate : gradient distributer
○ mul gate : swap multiplier
○ copy gate : gradient adder
○ max gate : gradient router
⑸ 기울기 하강 알고리즘(gradient descent algorithm)
① 개요
○ 정의 : 역전파(backpropagation)에서 얻은 기울기를 사용해 가중치를 업데이트하는 방법
○ 업데이트 방정식(update agorithm)이라고도 함
② 일반적으로 손실함수는 L2 손실함수를 따름
③ 행렬 표현으로 나타낸 업데이트 방정식
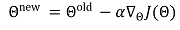
④ 단일 파라미터에 대한 업데이트 방정식

⑤ 한계 : 아직까지는 해결되지 않고 있음
○ 문제 1. surface가 convex function이 아니고 concave function이거나 saddle point일 수 있음
○ 문제 2. cost function이 미분 가능해야 함
○ 0/1 loss와 같은 경우 항상 미분 가능한 것은 아님
○ 또다른 미분 가능한 대체 함수를 사용하여 해결하려고 함
○ 문제 3. local minimum 근처에서는 학습이 빠르지 않음
⑥ 응용 1. stochastic gradient decent (SGD) : Rumelhart el al. (1988)에 의해 제안
○ 정의 : full gradient decent 방식이 오래 걸린다는 점을 보완하기 위해 randomly sampled subset을 고려하는 방식
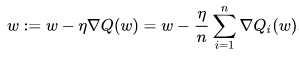
○ 종류 1. Mini-Batch SGD : 일반적으로 32, 64, 128, ···, 8192의 minibatch를 고려함
○ 종류 2. SGD : 가장 극단적인 방식은 single element의 결과로 parameter를 업데이트하는 것
○ time cost : Mini-Batch SGD < Full-Batch SGD < SGD
○ Mini-Batch SGD는 batch를 생성하여 gradient 연산에 들어가는 변수의 개수를 줄여 time cost를 줄일 수 있음
○ SGD는 오히려 batch를 생성하는 데 time cost가 발생
○ optimum loss value : Full-Batch SGD < Mini-Batch SGD < SGD
○ batch를 만드는 것은 정확도를 희생하는 대신 time cost를 절약할 수 있음
○ batch gradient decent는 이론적으로 수렴값에 영향을 주지 않지만 학습과정에서 노이즈를 만듦
⑹ 종류 3. 모멘텀(momentum)
① 기울기 방향으로 힘을 받으면 물체가 가속된다는 물리 법칙을 적용한 알고리즘
② 최적점까지 공이 굴러가는 듯한 움직임
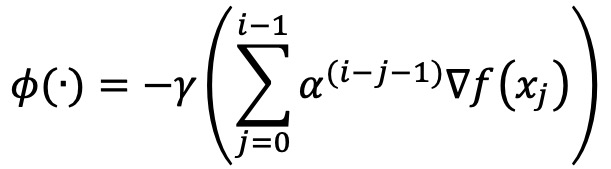
⑺ 종류 4. 네스테로프 모멘텀(NAG, Nesterov acceleraged gradient)
① 모멘텀 방향을 미리 적용한 위치에서 기울기를 계산하는 방법
⑻ 종류 5. AdaGrad(adaptive gradient algorithm)
① 손실함수의 기울기가 큰 첫 부분에서는 크게 학습하다가, 최적점에 가까워질수록 학습률을 줄여 조금씩 적게 학습하는 방식
⑼ 종류 6. Adam(adaptive moment estimation)
① 모멘텀 방식과 AdaGrad 방식의 장점을 합친 방식
② 모멘텀 방식처럼 공이 굴러가는 듯하지만 좌우 흔들림이 덜 함
⑽ 종류 7. RMSPro(root mean square prop)
① 기울기를 단순 누적하지 않고 지수 이동 평균을 사용하여 가장 최근의 기울기들이 더 크게 반영하도록 하는 기법
⑾ 종류 8. NAG(Nesterov's accelerated gradient) algorithm
⑿ 종류 9. L-BFGS(limited memory BFGS) algorithm
3. MLP 활용 [목차]
⑴ 예 1. 분류 알고리즘
⑵ 예 2. 시계열 예측(time-series prediction)
⑶ 예 3. 자기 연산 학습(auto-associative learning) : 오토인코더(autoencoder)라도고 함
입력: 2018.06.09 10:01
수정: 2021.11.21 22:29
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 7강. 차원 축소 알고리즘 (0) | 2021.12.03 |
|---|---|
| 【알고리즘】 16강. CNN 신경망 (0) | 2021.11.21 |
| 【알고리즘】 10강. 딥러닝 개요 (0) | 2021.11.21 |
| 【알고리즘】 4강. 데이터 시각화 (0) | 2021.10.28 |
| 【알고리즘】 1-1강. 정렬 알고리즘 실험 (0) | 2021.10.01 |



최근댓글