7강. 차원 축소 알고리즘(dimension reduction algorithm)
추천글 : 【알고리즘】 알고리즘 목차
1. 개요 [본문]
2. 종류 1. 주성분 분석 (PCA) [본문]
3. 종류 2. SNE, symmetric-SNE, tSNE [본문]
4. 종류 3. UMAP [본문]
5. 종류 4. SVD [본문]
6. 종류 5. ICA [본문]
7. 기타 [본문]
b. UMAP(uniform manifold approximation and projection)
1. 개요 [목차]
⑴ 차원 축소의 정의
① 고차원 데이터 X(1), ···, X(n) ∈ ℝp의 데이터가 주어져 있을 때,
② 적절한 subspace V ⊂ ℝp (단, dim(V) = k)를 찾고,
③ X의 V로의 투상(projection) X̃을 계산하는 것
④ unsupervised algorithm에 속함
⑵ 특징
① 정보 유지
② 모델 학습의 용이 : 머신러닝에 있어 더 적은 파라미터를 요하므로 더 빠르고 연산량이 적음
③ 결과 해석의 용이 : 주어진 고차원 데이터의 시각화
④ 노이즈 감소
⑤ 주어진 데이터의 진정한 dimensionality를 확인할 수도 있음
⑶ 방법
① 변수 선택(feature selection)
○ 가지고 있는 변수들 중 중요한 변수 몇 개만 고르고 나머지는 버리는 방법
○ 상관계수가 높거나 분산팽창지수(VIF, variance inflation factor)가 높은 변수 중 하나를 선택
② 변수 추출(feature extraction)
○ 모든 변수를 조합하여 이 데이터를 잘 표현할 수 있는 중요 성분을 가진 새로운 변수를 도출
○ 기존 변수를 조합해 새로운 변수를 만드는 기법
2. 종류 1. 주성분 분석(PCA, principal component analysis) [목차]
⑴ 개요
① 정의 : correlated variable을 orthogonal variable로 바꾸는 변환하는 차원 축소 기법
② 즉, 유의미한 몇 개의 진정한 직표좌표계만을 남기는 차원 축소 기법
③ orthogonal varible을 주성분이라고 하며, 주성분이 원본만큼 많은 정보량을 포함할 때 사용할 수 있음
④ 주어진 차원과 데이터의 진정한 차원이 다를 수 있다는 문제의식에서 출발
⑤ Pearson에 의해 1901년에 최초로 소개됨
⑥ 주성분 분석은 subspace (원점 지남)이 아니라 affine space에서도 정의할 수 있음
⑦ 즉, 평균값에 대해 정규화한 뒤 subspace에 대한 주성분 분석을 하면 됨
⑧ 주성분 분석은 주어진 데이터의 multivariate normality를 요하지 않음
⑵ 전제
① 데이터가 속한 공간의 기저를 각각 e1, ···, ep로 표시 (단, 기저집합이 직교집합일 필요는 없음)
○ e1, ···, ep는 주어진 차원을 나타내는 기저라고 할 수 있음 (단, 직교할 필요는 없음)
② 목표 : 다음과 같은 subspace의 직교 기저 Z1, ···, Zk를 찾아내는 것 (단, k < n) (일반적인 unsupervised problem 셋팅)
○ Z1, ···, Zk는 데이터의 진정한 차원을 나타내는 기저라고 할 수 있음

③ random vector
○ X는 특정 데이터 포인트를 나타냄 : x1, ···, xn은 각 성분
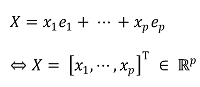
④ mean vector : population mean이라고도 함
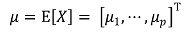
⑤ variance-covariance matrix
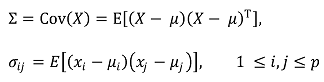
⑥ unbiased sample variance-covariance matrix : design matrix X, center matrix Xc에 대하여,
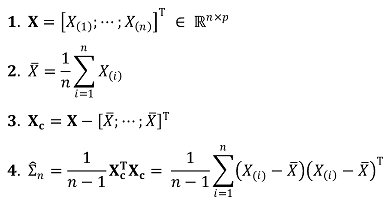
○ population variance-covariance matrix가 알려져 있지 않으면 사용함
○ X ∈ ℝn×p이므로 XTX ∈ ℝp×n × ℝn×p = ℝp×p
⑦ 목표 직교 기저의 표현
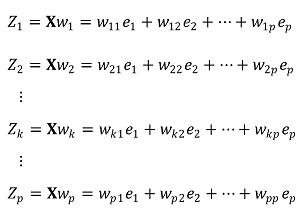
○ Zk := kth PC ∈ ℝp×1
⑧ 목표 직교 기저의 특징 : 선형대수학 개념으로 쉽게 유도됨
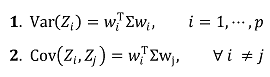
○ Var, Cov 등은 분산에 대한 특정 값이므로 ℝ1x1에 속함
○ variance-covariance matrix와 헷갈리지 말 것
⑶ 주성분 분석 문제 정의
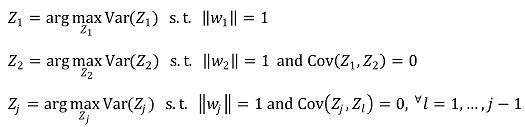
⑷ 주성분 분석 문제 풀이
① 방법 1. ∑의 eigen-decomposition
○ 각 좌표축에 있도록 잘 맞추면 공분산 행렬이 대각선 행렬이 되도록 할 수 있다.

○ 데이터가 변하는 방향을 각각 x, y, z 축 등으로 설정하면 x-y 등에서 공분산이 0이 될 것이라는 말이다.

○ 이때, (PTX)T = XTPTT = XTP이고, E[P] = P, E[PT] = PT임을 주의하자.
○ 그런데, P는 회전변환이므로 대각행렬이 곧 역행렬이므로 다음을 얻는다.

○ P = [p1, p2, ···, pN], Z = cov(X)라 정의하면,

○ 따라서 λi pi = Zpi로 λ는 고유 값(Eigenvalues), pi는 고유 벡터(eigenvectors)가 된다. 이제 특정 임계값 η보다 작은 고유값을 제거하고 남은 고유값들의 고유벡터들(서로 직교함)에 데이터 세트를 정사영시켜서 차원 축소를 할 수 있다.
○ 결론 1. d번째 주성분 PCd = d 번째로 큰 고유값(eigen value)에 대한 고유벡터
○ 결론 2. 고유값이 같은 고유벡터의 의미 : 대응하는 주성분의 크기가 같음
② 방법 2. center matrix Xc의 SVD(singular value decomposition) : 현재 PCA 알고리즘에서 표준 방법으로 채택
③ 방법 3. 등식 제약 하 라그랑주 승수법(Lagrange multiplier)
⑸ 축의 개수 결정
① 방법 1. fraction of total variance에 대한 scree plot
○ fraction of total variance의 정의
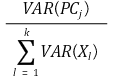
○ 도식화
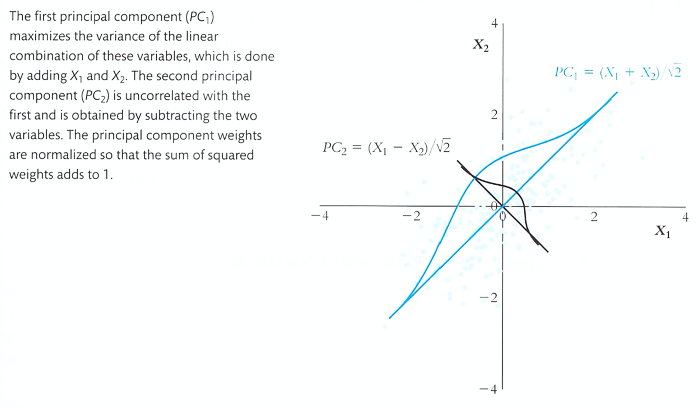
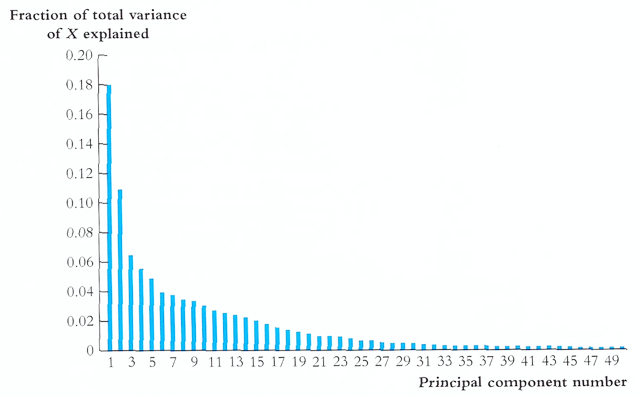
Figure. 2. scree plot : 각 성분 PC들이 설명하는 분산의 양을 표시
② 방법 2. eigen value에 대한 scree plot
③ 방법 3. in-sample 10-fold cross validation을 통해 MSPE를 최소로 하는 축의 개수 p 결정
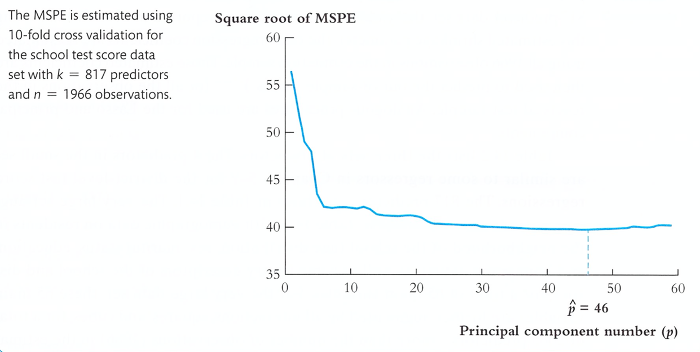
④ 나머지 축에 대한 정보를 잃어버리므로 PCA 알고리즘은 lossy compression algorithm의 기능을 수행함
⑹ 종합
① 예측 퍼포먼스 비교
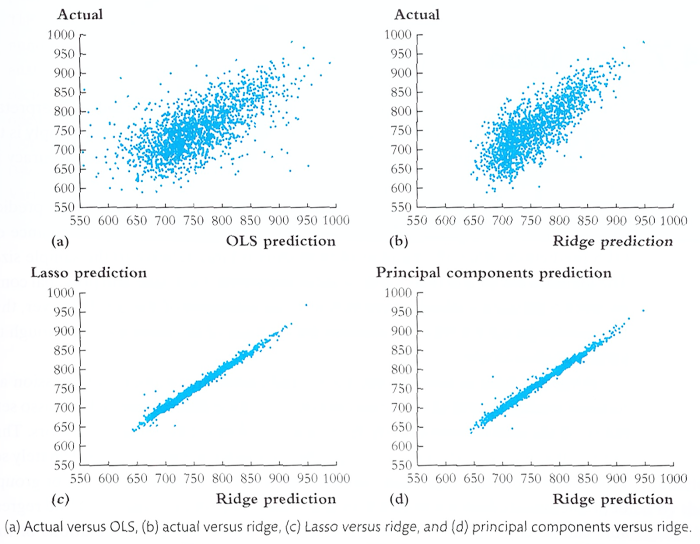
3. 종류 2. SNE, symmetric-SNE, tSNE [목차]
⑴ 데이터에서 지역 인접성(local neighborhoods)을 보존하려고 시도하는 차원 축소 알고리즘
⑵ 비선형적이며 비결정적
⑶ cost function, updating algorithm 등 딥러닝에 관한 지식을 요구함
5. 종류 4. 특이값 분해(SVD, singular value decomposition) [목차]
⑴ M × N 차원의 행렬 데이터에서 특이값을 추출하고 이를 통해 주어진 데이터의 차원을 축소하는 기법
6. 종류 5. 독립성분분석(ICA, independent component analysis) [목차]
⑴ 주성분 분석과 달리, 다변량의 신호를 통계적으로 독립적인 하부 성분으로 분리하여 차원을 축소하는 기법
⑵ 독립성분의 분포는 비정규분포를 따르게 됨
7. 기타 [목차]
⑴ 요인 분석(factor analysis)
① 정의 : 여러 개의 변수들로 이루어진 데이터에서 변수들 간의 상관관계를 고려하여 서로 유사한 변수들을 묶어 새로운 잠재요인을 추출하고 데이터 안의 구조를 해석하는 방법
② 데이터 안에 관찰할 수 없는 잠재적인 변수가 존재한다고 가정
③ 사회과학이나 설문조사에서 많이 활용
⑵ 다차원 척도법(MDS, multi-dimensional scaling)
① 정의 : 데이터 속에 잠재해 있는 패턴, 구조를 찾아내어 소수 차원의 공간에 기하학적으로 표현하는 객체 간 근접성 및 개체들 간 집단화를 시각화하는 통계 기법
② 개체들 사이의 유사성, 비유사성을 측정하여 2차원 또는 3차원 공간 상에 점으로 표현
⑶ 선형 판별 분석(LDA, linear discriminant analysis)
① 정의 : PCA와 유사하게 데이터를 저차원 공간에 투영해 차원을 축소하는 방법
⑷ CCA(canonical-correlation analysis) : Seurat 파이프라인에서 사용함
⑸ RPCA(reciprocal principal component analysis) : Seurat 파이프라인에서 사용함
⑹ PHATE
⑺ ODA
⑻ LLE
⑼ LSA
⑽ PLSA(probabilistic latent semantic analysis)
① latent class model로부터 혼합된 성분을 decomposition 할 때 사용
② 응용 : 질량 분석 데이터에서 차원축소 성분을 뺄 때 사용
입력: 2021.12.3 16:22
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 6강. 분류 알고리즘 (0) | 2021.12.11 |
|---|---|
| 【알고리즘】 23강. MAB(multi-armed bandits) (0) | 2021.12.10 |
| 【알고리즘】 16강. CNN 신경망 (0) | 2021.11.21 |
| 【알고리즘】 15강. 다층 퍼셉트론 (0) | 2021.11.21 |
| 【알고리즘】 10강. 딥러닝 개요 (0) | 2021.11.21 |





최근댓글