23강. 베이지안 최적화와 MAB
추천글 : 【알고리즘】 알고리즘 목차
1. 개요 [목차]
⑴ MAB(multi-armed bandits)
① 문제 정의 : 가장 payoff가 높은 최적의 arm을 선택하는 것
② 다음과 같은 상황에서 특히 필요
○ 목적 함수를 계산하기 어려운 경우 (black-box algorithm)
○ 명시적인 분석적 형태(analytic form)가 없는 경우
○ 특이값(singular value)이 존재하는 경우
○ 미분 가능하지 않은 경우
○ 데이터에 노이즈가 많은 경우
⑵ 두 가지 전략의 trade-off
① exploitation : 현재 가지고 있는 데이터로부터 얻은 empirical mean을 가지고 reward를 극대화하는 것
② exploration : empirical mean이 true mean과 일치하도록 개선하는 것
③ 우연히 초기 데이터가 데이터의 진실한 분포와 다른 경우 exploration을 게을리 하면 잘못된 판단을 고칠 수 없음
⑶ 종류 1. 베이지안 최적화(Bayesian optimization)

○ 각 arm의 reward distribution에 대해 사전 분포(prior distribution, surrogate model)이 주어져 있음
○ 주로 사용되는 prior 모델은 가우시안 프로세스
○ 각 reward를 관측할 때마다 사후 분포(posterior distribution)를 얻게 됨
② 획득함수 : 다음 보상이 극대화되도록 샘플링을 수행함

○ 모든 획득 함수는 사후 분포를 기반으로 평균 μ(x)와 분산 σ2(x)을 계산하며, 이를 통해 탐색 전략을 설계
○ 종류 1. EI(expected improvement) : 다음 수식에서 EI(x)에 대한 두 번째 식은 가우시안 프로세스일 때만 성립함
○ 단, Φ와 𝜙는 표준정규분포의 CDF와 PDF이고 Z는 x를 표준화한 것
○ λ가 클수록 exploration을 더 많이 하게 됨

○ 종류 2. MPI(maximum probability of improvement)
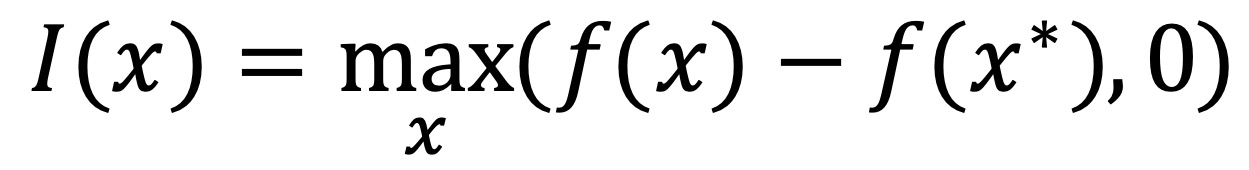
○ 종류 3. UCB
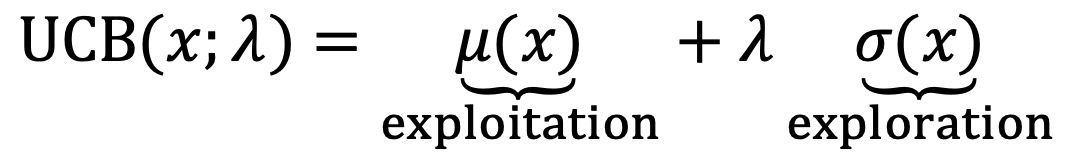
③ 가우시안 프로세스(Gaussian process) : 베이지안 최적화 중 정규분포 가정을 하는 경우
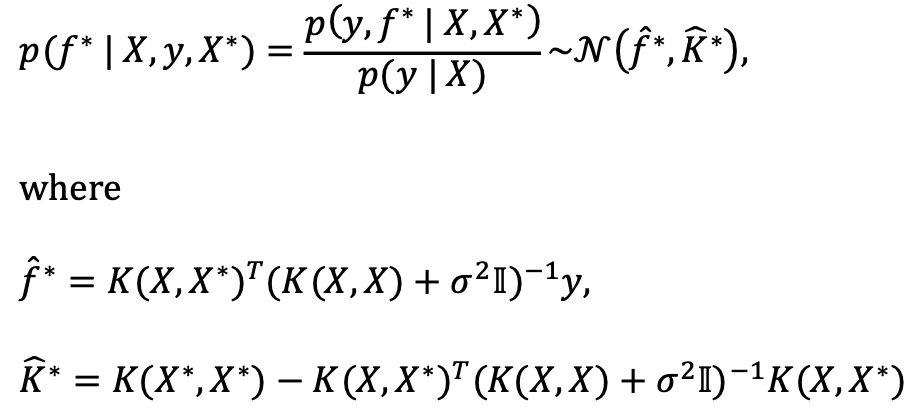
x <- c(-3, -1, 0, 2, 3)
f <- data.frame(x=x, y=cos(x))
x <- f$x
k_xx <- varCov(x,x)
k_xxs <- varCov(x, x_star)
k_xsx <- varCov(x_star, x)
k_xsxs <- varCov(x_star, x_star)
f_star_bar <- k_xsx %*% solve(k_xx)%*%f$y # Mean
cov_f_star <- k_xsxs - k_xsx %*% solve(k_xx) %*% k_xxs # Var
plot_ly(type='scatter', mode="lines") %>%
add_trace(x=x_star, y=f_star_bar, name="Function Estimate") %>%
add_trace(x=x_star, y=f_star_bar-2*sqrt(diag(cov_f_star)),
name="Lower Confidence Band (Function Estimate)",
line = list(width = 1, dash = 'dash')) %>%
add_trace(x=x_star, y=f_star_bar+2*sqrt(diag(cov_f_star)),
name="Upper Confidence Band (Function Estimate)",
line = list(width = 1, dash = 'dash')) %>%
add_markers(x=f$x, y=f$y, name="Obs. Data", marker=list(size=20)) %>%
add_trace(x=x_star, y=cos(x_star),line=list(width=5), name="True f()=cos(x)") %>%
layout(title="Gaussian Process Simulation (5 observations)", legend = list(orientation='h'))
④ 하이퍼파라미터 최적화
○ 최대 우도 추정(MLE)을 통해 주어진 데이터 X와 y가 발생할 확률(marginal likelihood)을 최대화하는 하이퍼파라미터를 탐색
○ marginal likelihood 및 가우시안 프로세스의 하이퍼파라미터는 다음과 같이 정의됨

○ 장점 : underfitting 및 overfitting 개선
⑤ 레퍼런스
○ Osband, Russo, and Van Roy 2013
○ Rusoo and Van Roy 2014, 2015, 2016
○ Bubeck and Liu 2013
○ Data Science and Predictive Analytics (UMich HS650) (PI: Ivo Dinov)
⑷ 종류 2. stochastic multi-armed bandit
① 특징 1. online decision : 각 시간 t = 1, ···, T에서 N개의 arm 중 it번째 arm을 선택
② 특징 2. stochastic feedback : 각각의 arm이 제공하는 보상은 정해져 있지만 알려져 있지 않은 분포를 따름
③ 특징 3. bandit feedback : 각 시간 단계에서 내가 선택한 arm에 대한 보상만 볼 수 있음
④ 목표 : 전체 T 단계에 걸친 cumulative expected rewards를 최대화하는 것
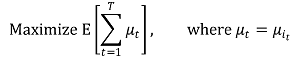
⑤ reward를 최대화하는 것은 regret = μ* - μt를 최소화하는 것과 동일함
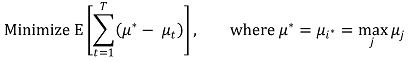
⑥ bandit : 강도처럼 실패했을 때 뺏어간다는 의미
⑦ 예시 : Thomson sampling
○ UCB와 함께 현존하는 전체 bandit 알고리즘 중 가장 많이 쓰이는 알고리즘
2. UCB(upper confidence bound) [목차]
⑴ 톰슨 샘플링과 함께 현존하는 전체 bandit 알고리즘 중 가장 많이 쓰이는 알고리즘
⑵ 수식화
① t까지의 시간 동안 arm i에서의 empirical mean
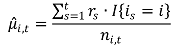
○ 분자 : arm i에서 얻어진 reward의 총합
○ I{is = i} : is = i인 경우에만 1을 출력하고 나머지는 0인 함수
○ ni,t : t까지의 시간 동안 i가 뽑아진 횟수
② UCB(upper confidence bound)
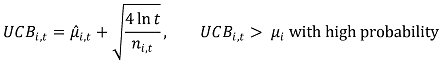
○ optimism : 실제 기댓값보다 높은 확률로 더 높게 본다는 의미
○ 높은 확률 : 99.9% 이상
③ 각 단계에서 UCB가 최대인 arm을 선택
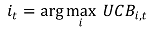
④ 매 시간 단계마다 empirical mean과 UCB를 업데이트
○ 한 번씩 관측할 때마다 uncertainty를 나타내는 UCB가 줄어듦
⑶ 수렴성 증명
① regret의 정의 : 임의의 시간 T에 대하여,
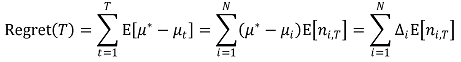
② 수렴성 : 수학적으로 엄밀하게 증명됨
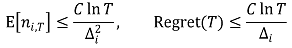
③ 결론
○ per time regret은 0으로 수렴함 : 매 선택이 최선의 선택이 된다는 의미
○ UCB가 아니라 empirical mean을 가지고 하면 그러한 arm의 선택이 optimal하다는 보장이 없음
○ 즉, optimal arm을 한 번도 시도하지 않은 경우가 생김
⑷ UCB와 톰슨 샘플링의 비교
① 공통점 1. total regret은 O(log T) : per time regret은 O(log T / T)로 0으로 수렴함
② 차이점 1. thomson sampling이 많은 경우 UCB보다 좋음 : 즉, UCB는 조금 더 보수적인 알고리즘으로 조금 늦게 수렴함
③ 차이점 2. UCB는 deterministic하고 thomson sampling은 probabilistic (randomized)
3. 톰슨 샘플링(Thomson sampling) [목차]
⑴ 개요
① 가장 오래된 bandit 알고리즘 : thomson에 의해 1933년에 소개됨
② 자연스럽고 효율적인 휴리스틱 알고리즘
⑵ 과정
① 각 arm에 대한 파라미터의 belief를 유지함 (예 : mean reward)
○ prior distribution은 Beta 분포, Gaussian 분포 등을 이용함
② 각 prior distribution으로부터 estimated reward를 추출
○ 단순한 샘플링을 의미하므로 기댓값을 추출하는 것이 아님
○ 관측값이 적으면 분산이 증가하는데 이 경우에 쉽게 추출될 수 있게 하기 위함
③ estimated reward가 최대인 arm을 선택하고 그 arm에 대한 posterior reward를 관찰
○ posterior distribution은 항상 연구자가 가지고 있어야 함
④ posterior를 Bayesian 방식에 대입하여 prior belief를 업데이트함
⑤ mode가 두 개여도 잘 working 함
⑶ 예시 : Beta 분포를 이용한 Thomson sampling
① 모든 arm에 대해 Beta(1, 1)을 prior belief로 하여 시작
② 각 시간 t에 대하여,
○ prior : Beta(α, β)
○ 각 arm에 대해 독립적으로 θi,t를 추출
○ it = argmaxi θi,t인 it를 선택
○ Beta(α+1, β) : 1을 관찰한 경우
○ Beta(α, β+1) : 0을 관찰한 경우
⑷ 예시 : Gaussian 분포를 이용한 Thomson sampling
① 모든 arm에 대해 N(0, ν2)을 prior belief로 하여 시작
② 각 시간 t에 대하여,
○ prior : N(0, ν2)
○ 각 arm에 대해 독립적으로 θi,t를 추출
○ it = argmaxi θi,t인 it를 선택
○ 그 arm에 대하여 empirical mean µˆ을 업데이트 (posterior) : 이때 n은 독립된 관측의 횟수
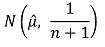
⑸ 수렴성
① 일정 횟수 이후에는 두 arm 간의 well-separation이 결국 best arm을 만들도록 하게 됨
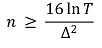
② Beta 분포
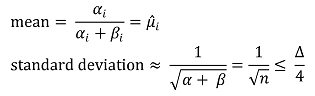
③ Gaussian 분포 : Azuma-Hoeffding inequality에 근거함
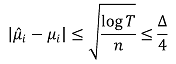
⑹ UCB와 톰슨 샘플링의 비교
① 공통점 1. total regret은 O(log T) : per time regret은 O(log T / T)로 0으로 수렴함
② 차이점 1. thomson sampling이 많은 경우 UCB보다 좋음 : 즉, UCB는 조금 더 보수적인 알고리즘으로 조금 늦게 수렴함
③ 차이점 2. UCB는 deterministic하고 thomson sampling은 probabilistic (randomized)
입력: 2021.12.10 00:52
수정: 2024.11.21 15:30
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 11강. 강화학습 (0) | 2021.12.13 |
|---|---|
| 【알고리즘】 6강. 분류 알고리즘 (0) | 2021.12.11 |
| 【알고리즘】 7강. 차원 축소 알고리즘 (0) | 2021.12.03 |
| 【알고리즘】 16강. CNN 신경망 (0) | 2021.11.21 |
| 【알고리즘】 15강. 다층 퍼셉트론 (0) | 2021.11.21 |




최근댓글