11강. 강화학습(reinforcement learning; RL)
추천글 : 【알고리즘】 알고리즘 목차
1. 개요 [본문]
2. Markov chain [본문]
3. Markov decision process [본문]
4. Markov chain Monte Carlo [본문]
1. 개요 [목차]
⑴ 정의
① (참고) supervised learning
○ 데이터 : (x, y) (단, x는 feature, y는 label)
○ 목표 : 맵핑 함수 x → y의 계산
② (참고) unsupervised learning
○ 데이터 : x (단, x는 feature이고 label은 없음)
○ 목표 : x의 underlying structure에 대한 학습
③ reinforcement learning
○ 데이터 : (s, a, r, s') (단, s는 state, a는 action, r은 reward, s'은 다음 상태)
○ 목표 : 여러 시간에 걸친 reward의 총합을 최대화
⑵ 특징 : supervised learning, unsupervised learning과는 차별성이 있음
① 정답을 묵시적으로 제공받음 : reward의 형태로 제공받음
② 환경과의 상호작용을 고려해야 함 : delayed feedback 등이 문제가 됨
③ 이전의 결정이 미래의 상호작용에 영향을 줌
④ 적극적으로 정보를 얻는 알고리즘 : 강화학습은 데이터를 얻는 과정까지를 포함함
⑶ 요소 1. reward
⑷ 요소 2. policy
① 정의 : agent의 행동. 즉, state를 입력으로 action을 출력으로 하는 맵핑
② 종류 1. deterministic policy
③ 종류 2. stochastic policy
○ 이유 1. learning에서 최적의 행위를 모르므로 exploration을 하기 위함
○ 이유 2. 최적의 상황이 stochastic한 걸 수도 있음 (예 : 가위바위보, 상대방이 역이용하는 경우)
⑸ 요소 3. value function
① 정의 : 미래의 reward에 대한 기댓값을 평생 가치(생애 가치, VLT)로 나타낸 것
② 수식화 : state s, policy π, 미래가치를 현재가치로 보정하기 위한 계수 γ에 대하여,
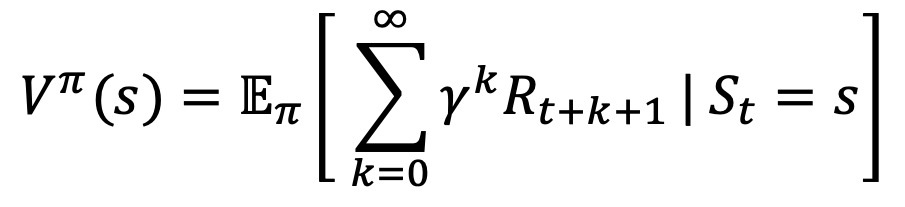
③ state가 좋은지 나쁜지를 평가하여 action을 선택하는 근거를 제공
⑹ 요소 4. model
① 정의 : 환경(environment)의 행동
② 주어진 state와 action에 대하여 model은 다음 state와 reward를 결정함
③ model-free method와 model-based method가 있음을 유의
2. Markov chain (Markov process) [목차]
⑴ 정의 : 미래 상태가 현재 상태에만 의존하고, 과거 상태에는 의존하지 않는다는 시스템

① strongly connected (= irreducible) : 그래프 내 임의의 노드 i에서 다른 임의의 노드 j로 도달할 수 있는 상태
② period : 특정 노드 i의 period는 노드 i에서 i로 향한는 모든 path의 최대공약수
○ 예 : 두 개의 노드 A, B가 있고 A=B와 같이 두 개의 엣지로 연결돼 있으면 각 노드의 period는 2
③ aperiodic : 모든 노드의 period가 1인 것
○ aperiodic ⊂ irreduicible
○ 예 : 각 노드가 자기 자신으로 향하는 walk가 있으면 aperiodic
④ 정상 상태(stationary state) : Pr(xn | xn-1)이 n에 무관하면 Markov process는 stationary (time-invariant)
⑤ regular
○ regular ⊂ irreduicible
○ 어떤 자연수 k에 대해, transition matrix M의 거듭제곱 Mk의 모든 원소가 양수(즉, 0이 아닌 값)인 경우
⑵ two-state Markov chain : 그래프 이론과 밀접한 관련이 있음
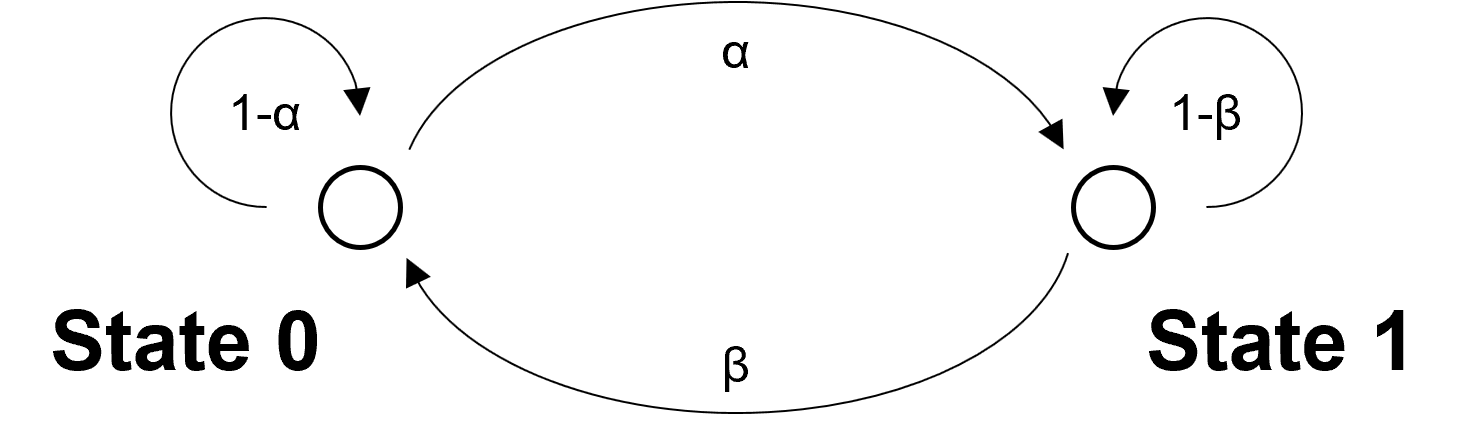
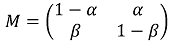
Figure. 1. two-scale Markov chain
① M : 1 step으로 state transition이 일어나는 변환
② Mn : n step으로 state transition이 일어나는 변환
③ steady-state vector : Mq = q를 만족하는 q. 즉, 고유치가 1인 고유벡터
⑶ HMM(hidden Markov model)
① χ = {Xi}가 Markov process이고 Yi = ϕ(Xi) (단, ϕ는 deterministic fuction)이면 y = {Yi}는 hidden Markov model
② Baum-Welch 알고리즘
○ 목적 : HMM 파라미터 학습
○ 입력 : 관측된 데이터
○ 출력 : HMM의 상태 전이 확률과 방출 확률
○ 원리 : EM(expectation maximization) 알고리즘의 일종
○ 수식화
○ Akl : 상태 k에서 상태 l로의 전이 횟수
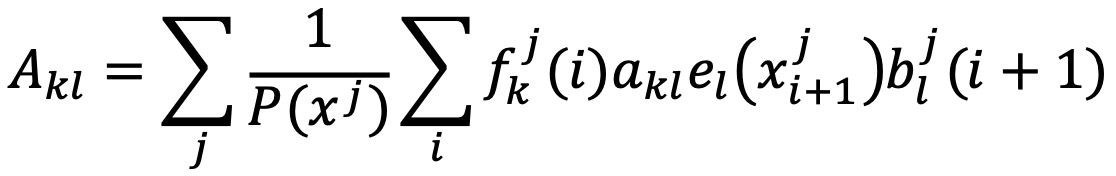
○ Ek(b) : 상태 k에서 관측값 b의 방출 횟수
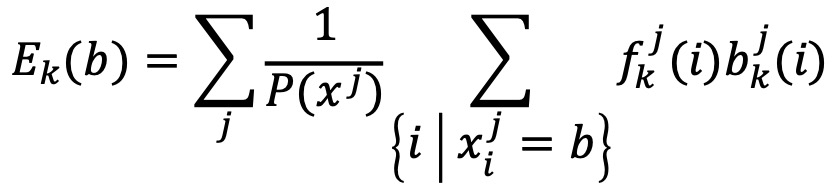
○ Bk : 상태 k의 초기 확률
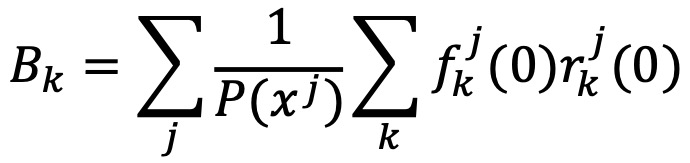
③ Viterbi 알고리즘 (ref)
○ 목적 : 주어진 HMM에서 가장 가능성이 높은 숨겨진 상태의 시퀀스를 찾는 데 사용됨
○ 입력 : HMM의 파라미터와 관측된 데이터
○ N : 가능한 숨겨진 상태의 개수
○ T : 주어진 관측 데이터의 길이
○ A : 상태 전이 확률(state transition probability). akl = 상태 k에서 상태 l로 전이할 확률
○ E : 관측 확률(emission probability). ek(x) = 상태 k에서 관측 x가 나타날 확률
○ B : 초기 상태 확률(initial probability)
○ 출력 : 가장 가능성이 높은 상태 시퀀스
○ 원리 : 동적 프로그래밍(dynamic programming)을 이용해 최적의 경로를 계산
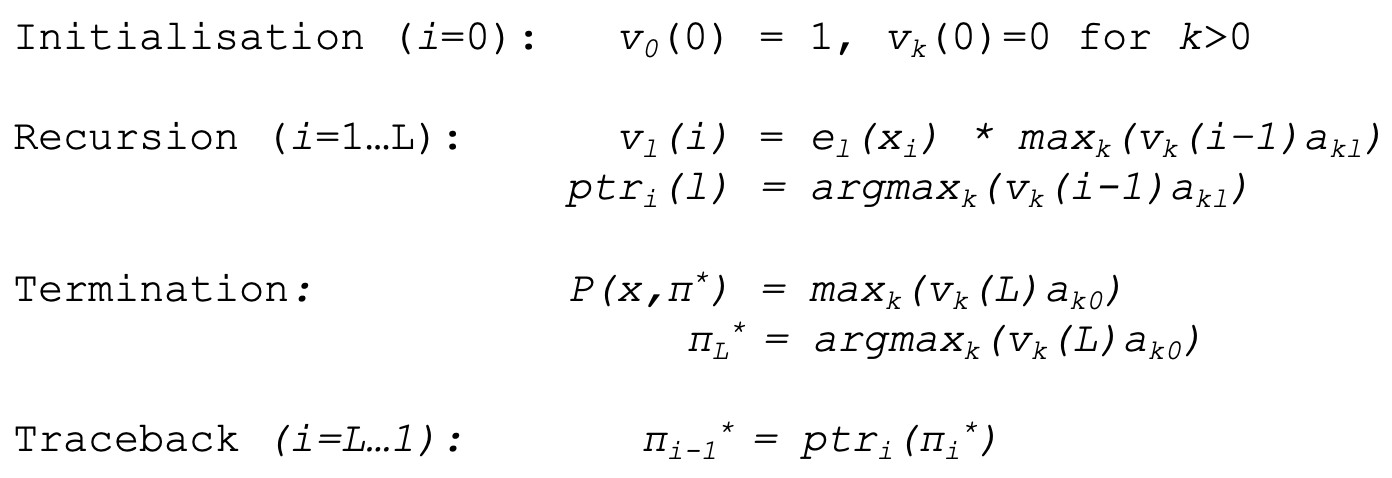
○ 단계 1. 초기화
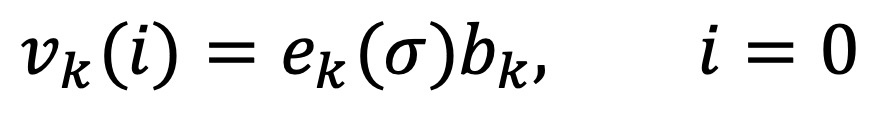
○ bk : 상태 k의 초기 확률 P(s0 = k)
○ ek(σ) : 상태 k에서 첫 번째 관측 σ가 나올 확률 P(x0 | s0 = k)
○ 단계 2. 재귀(recursion)
○ 각 시점 i = 1, ···, T까지 모든 상태에 대해 이전 시점에서 온 최대 확률을 계산 : 다음과 같이 이전 상태에 대한 점화식이 성립
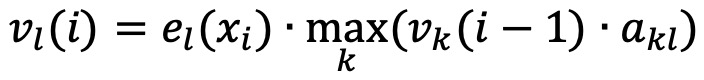
○ 가장 가능성이 높은 이전 상태를 저장하는 backpointer (ptr) 계산
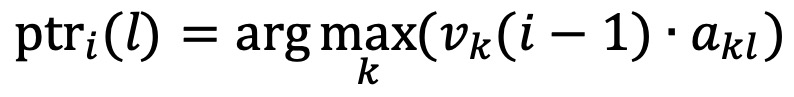
○ ptri(l)은 현재 상태 l로 오는 데 가장 높은 확률을 갖는 이전 상태 k를 저장하는 역할을 함
○ 단계 3. 종료(termination)
○ 최종 시점에서 가장 높은 확률을 선택
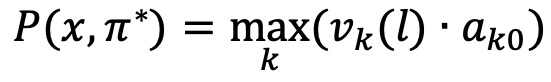
○ 최적 상태 시퀀스의 마지막 상태를 결정
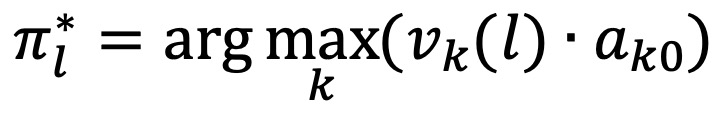
○ vk(i - 1) : 이전 시점 i - 1에서 상태 k에 있었을 때의 최적 확률값
○ akl : 상태 k에서 l로 전이할 확률
○ 단계 4. 역추적(traceback)
○ i = T, ···, 1에 대해 ptr 배열을 따라가면서 최적 경로를 복원
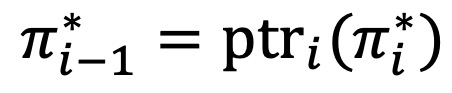
○ 예시
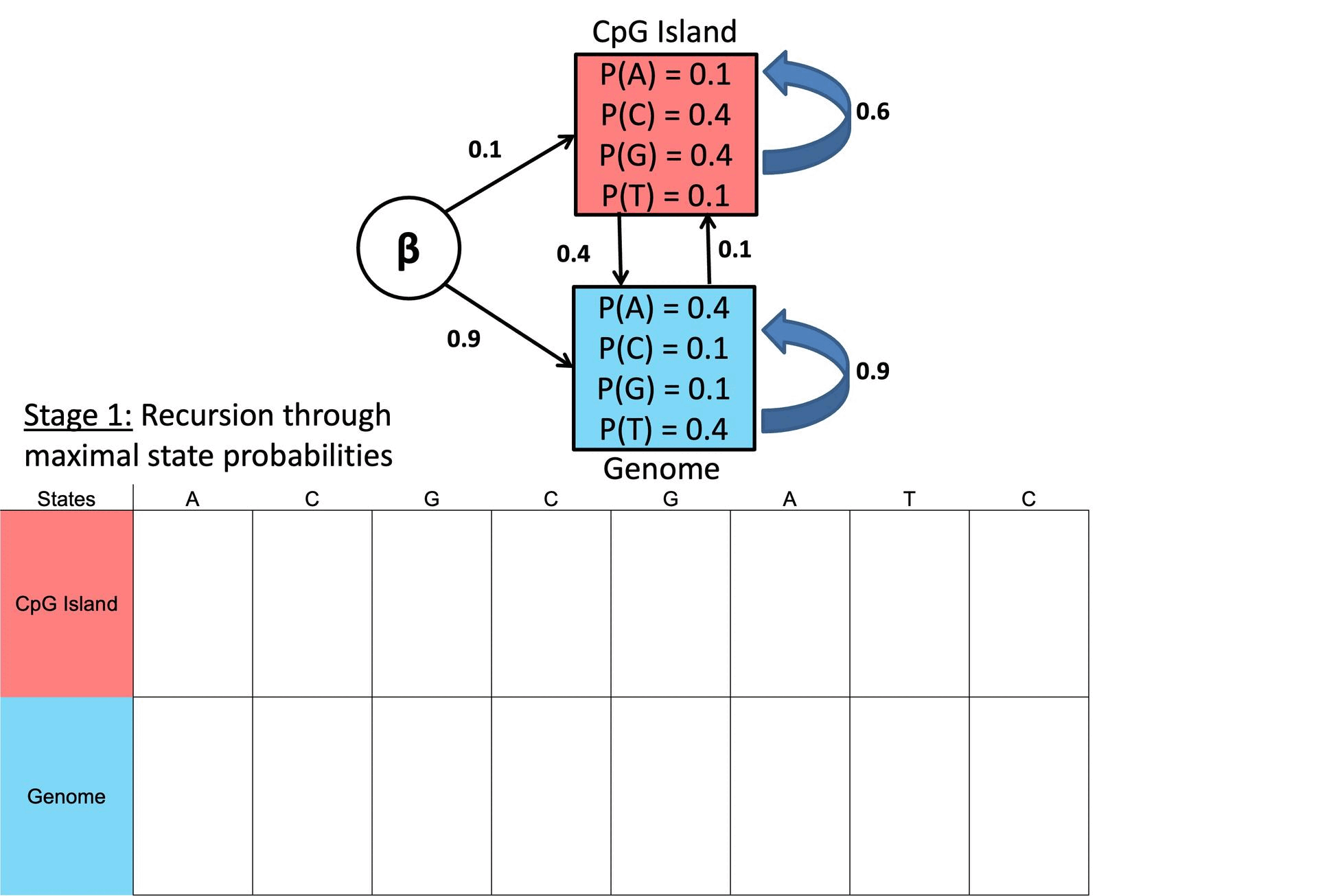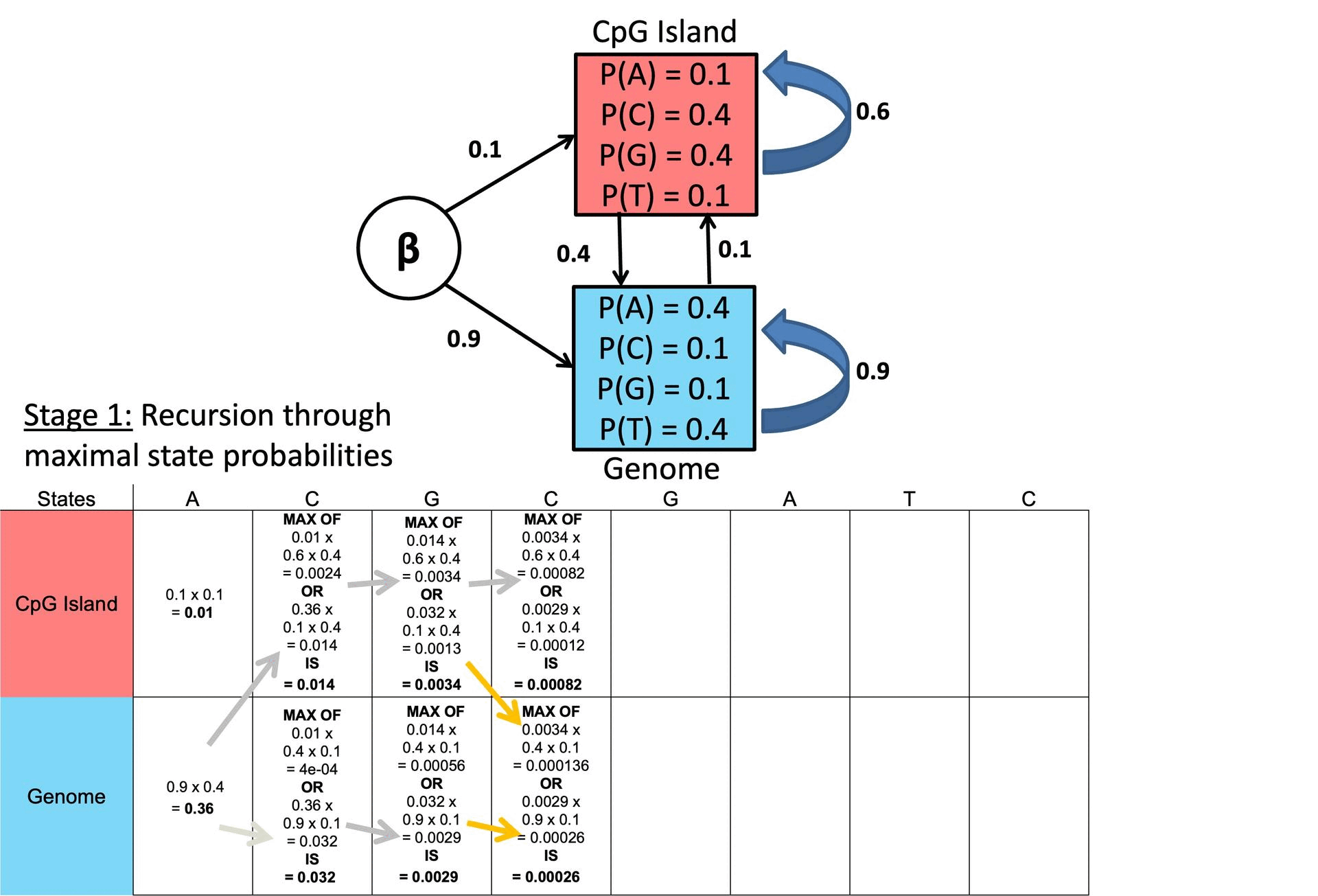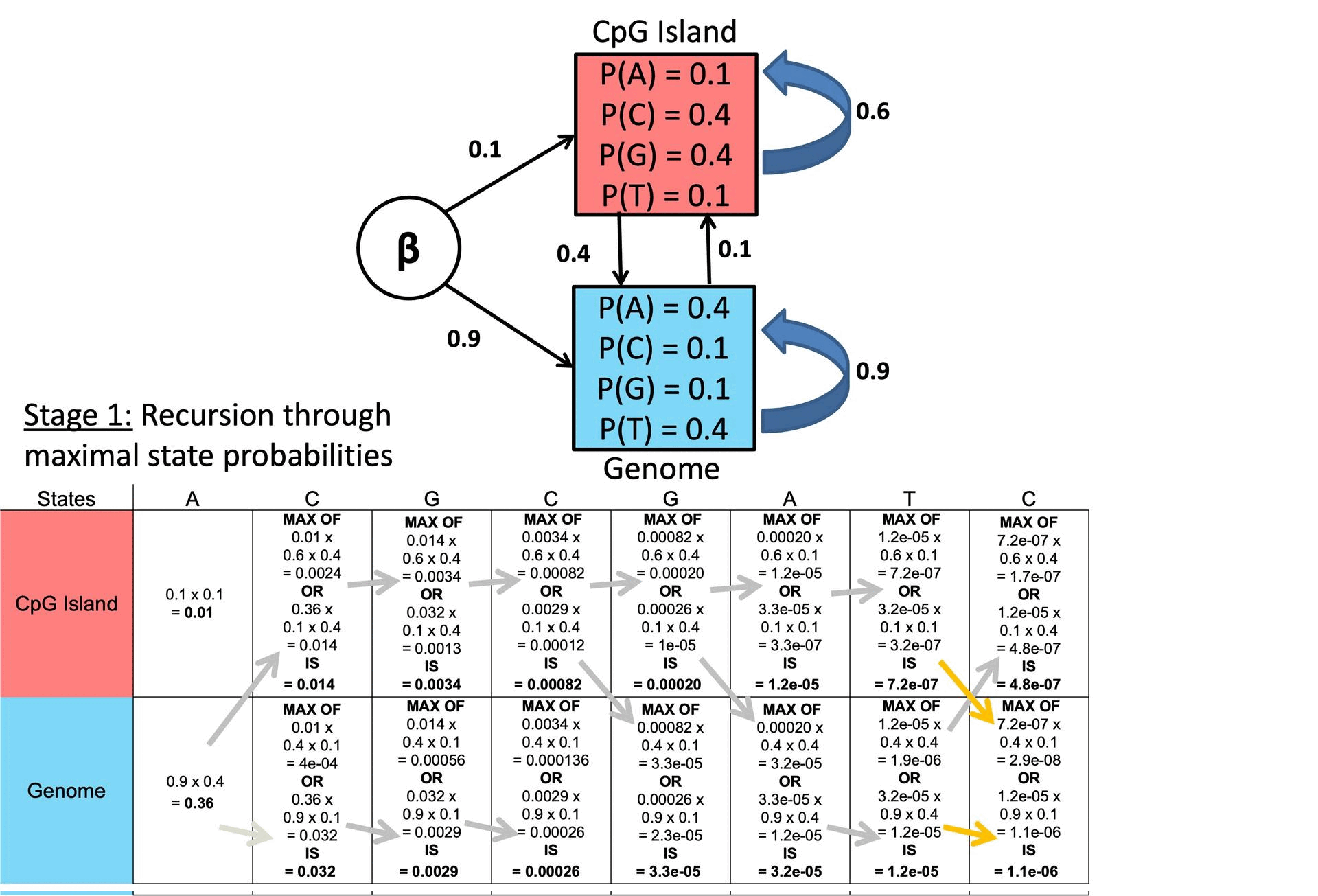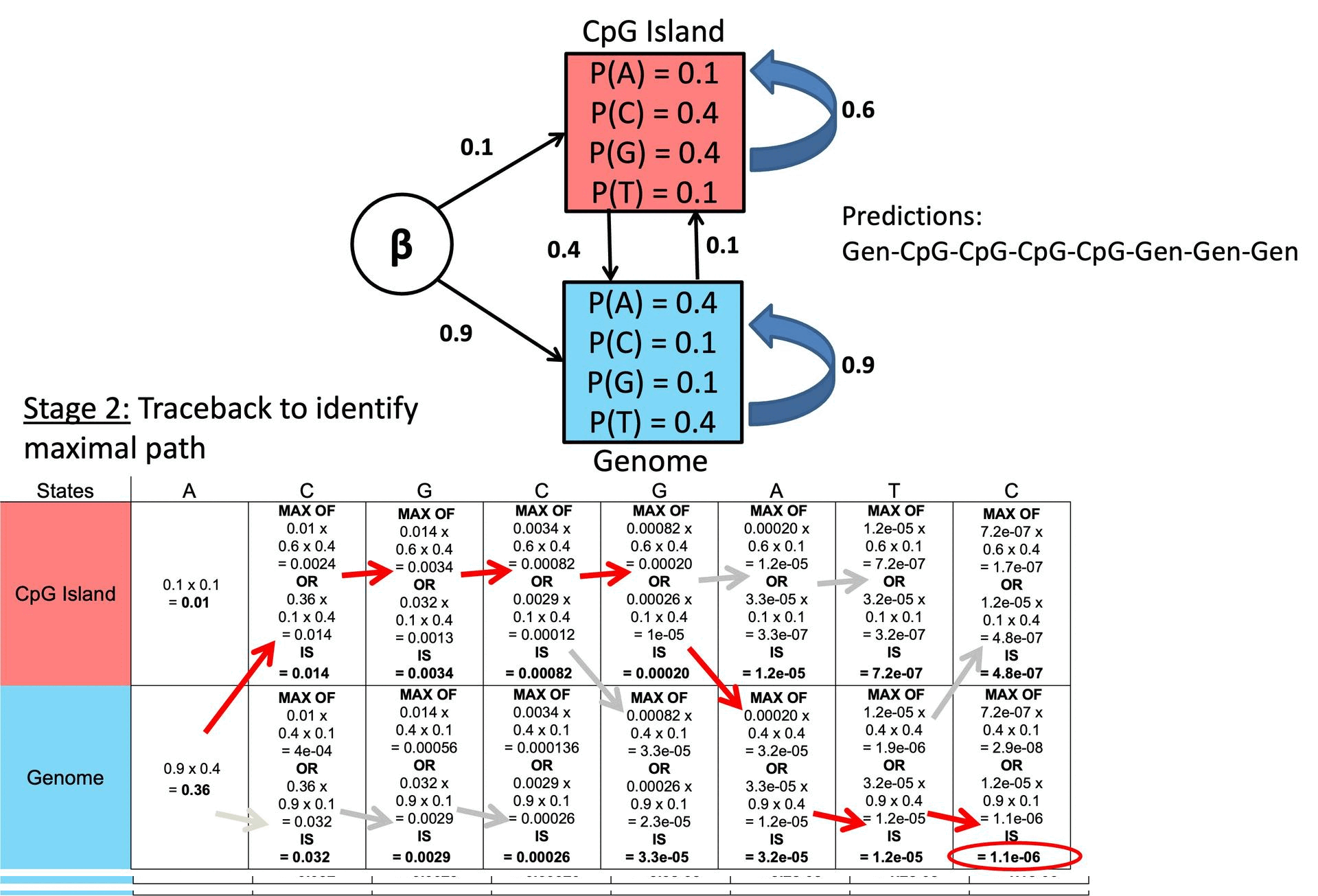
Figure. 2. Viterbi 알고리즘 예시
○ 파이썬 코드
class HMM(object):
def __init__(self, alphabet, hidden_states, A=None, E=None, B=None):
self._alphabet = set(alphabet)
self._hidden_states = set(hidden_states)
self._transitions = A
self._emissions = E
self._initial = B
def _emit(self, cur_state, symbol):
return self._emissions[cur_state][symbol]
def _transition(self, cur_state, next_state):
return self._transitions[cur_state][next_state]
def _init(self, cur_state):
return self._initial[cur_state]
def _states(self):
for k in self._hidden_states:
yield k
def draw(self, filename='hmm'):
nodes = list(self._hidden_states) + ['β']
def get_children(node):
return self._initial.keys() if node == 'β' else self._transitions[node].keys()
def get_edge_label(pred, succ):
return (self._initial if pred == 'β' else self._transitions[pred])[succ]
def get_node_shape(node):
return 'circle' if node == 'β' else 'box'
def get_node_label(node):
if node == 'β':
return 'β'
else:
return r'\n'.join([node, ''] + [
f"{e}: {p}" for e, p in self._emissions[node].items()
])
graphviz(nodes, get_children, filename=filename,
get_edge_label=get_edge_label,
get_node_label=get_node_label,
get_node_shape=get_node_shape,
rankdir='LR')
def viterbi(self, sequence):
trellis = {}
traceback = []
for state in self._states():
trellis[state] = np.log10(self._init(state)) + np.log10(self._emit(state, sequence[0]))
for t in range(1, len(sequence)):
trellis_next = {}
traceback_next = {}
for next_state in self._states():
k={}
for cur_state in self._states():
k[cur_state] = trellis[cur_state] + np.log10(self._transition(cur_state, next_state))
argmaxk = max(k, key=k.get)
trellis_next[next_state] = np.log10(self._emit(next_state, sequence[t])) + k[argmaxk]
traceback_next[next_state] = argmaxk
trellis = trellis_next
traceback.append(traceback_next)
max_final_state = max(trellis, key=trellis.get)
max_final_prob = trellis[max_final_state]
result = [max_final_state]
for t in reversed(range(len(sequence)-1)):
result.append(traceback[t][max_final_state])
max_final_state = traceback[t][max_final_state]
return result[::-1]
④ 종류 1. PSSM : 단순한 HMM 구조
⑤ 종류 2. profile HMM : PSSM에 비해 다음과 같은 장점을 가짐
○ profile HMM 모식도
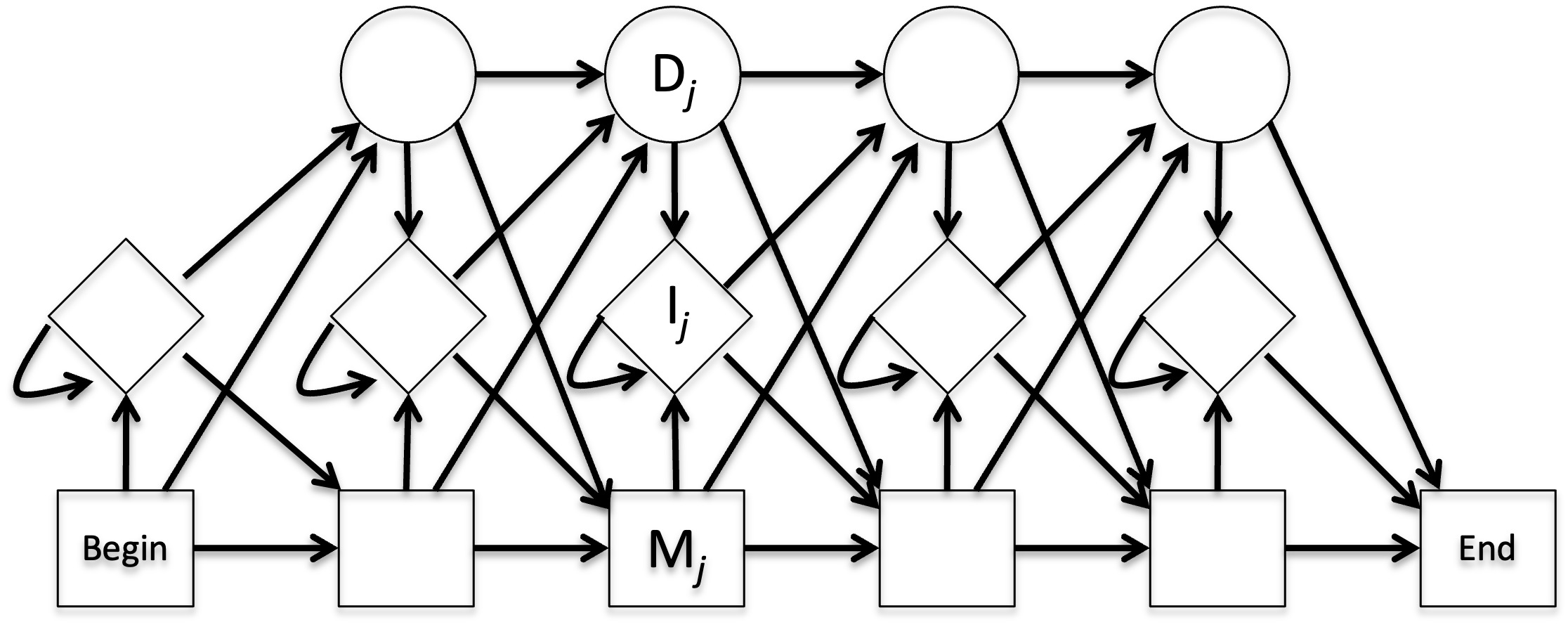
Figure. 3. profile HMM 모식도
○ M, I, D는 각각 match, insertion, deletion을 나타냄
○ Mi는 Mi+1, Ii, Di+1로 갈 수 있음
○ Ii는 Mi+1, Ii, Di+1로 갈 수 있음
○ Di는 Mi+1, Ii, Di+1로 갈 수 있음
○ 장점 1. insertion, deletion을 모델링할 수 있음
○ 장점 2. transition은 유효한 상태 간 이동으로 제한됨
○ 장점 3. 상태 간 경계가 잘 정의됨
⑷ 성질 1. Perron-Frobenius theorem
① 정리 1. transition matrix가 P인 Markov chain이 strongly connected이면 오직 1개의 정상상태 분포 q가 존재
○ 정상상태 분포는 Pq = q를 만족함
② 정리 2. transition matrix가 P인 Markov chain이 strongly connected이고 aperiodic이면,
○ Pij : 노드 j에서 노드 i로 전이될 확률. ∑i Pij = 1
○ 2-1. Pk의 i행 j열 원소 Pij(k)는 k → ∞로 갈 때 qi로 수렴 : 이때 i만 같으면 j와 무관하게 같은 값으로 수렴함을 주목
○ 2-2. 초기상태 x0에 무관하게 k번째 상태 xk는 k → ∞로 갈 때 q로 수렴
⑸ 성질 2. Markov process으로 열역학 제2법칙(엔트로피 증가 법칙)을 증명할 수 있음
① 확산의 법칙을 시뮬레이션 할 수 있기 때문 : 단, uniform stationary distribution 가정
② 관련 개념 : random walk
3. Markov decision process (MDP) [목차]
⑴ 개요
① 정의 : transition과 관련하여, t+1에서의 상태가 오직 t에서의 상태의 함수로 결정되는 것
② 모식도
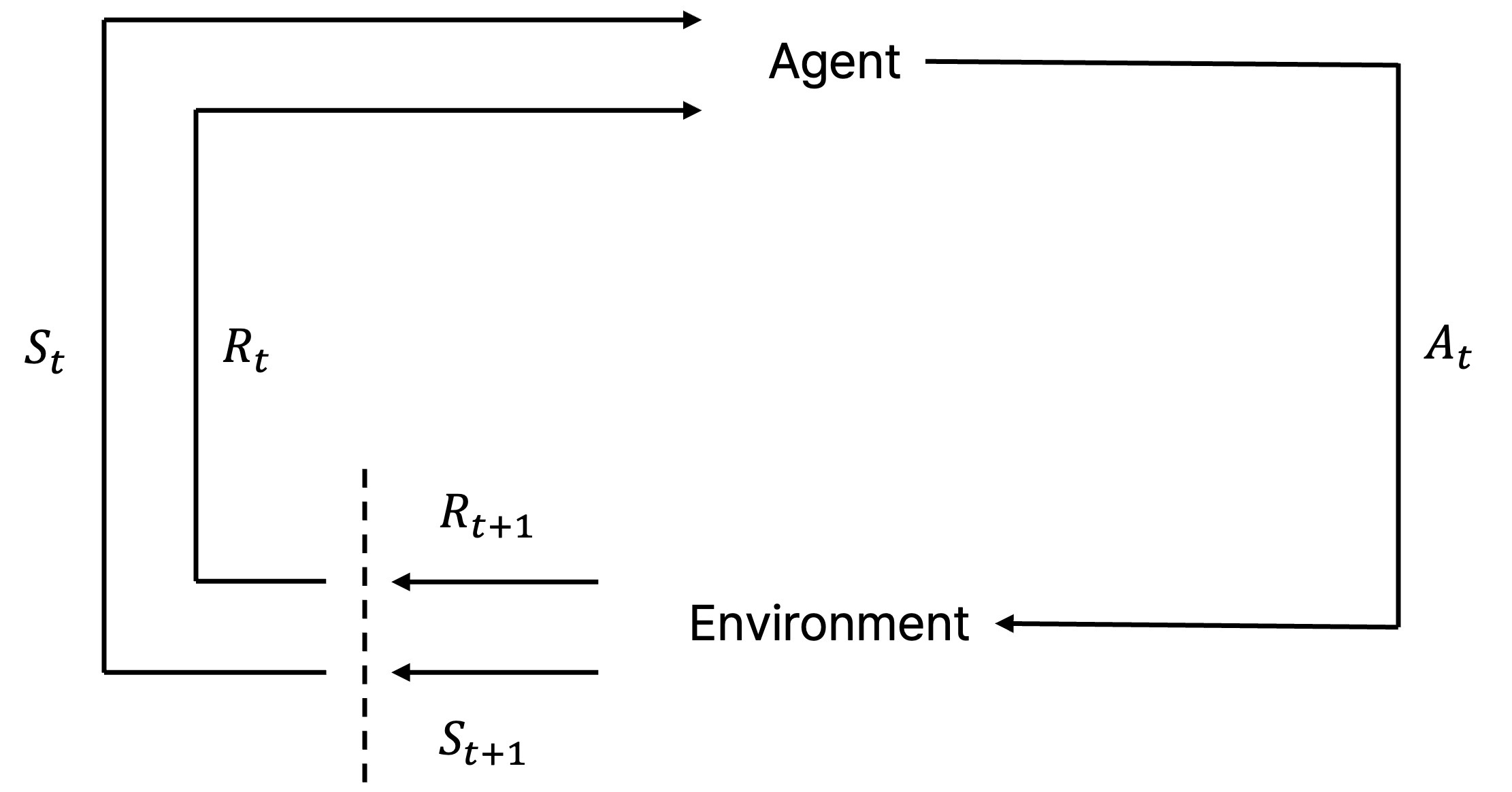
Figure. 4. MDP에서 agent-environment interaction
○ state : st ∈ S
○ action : at ∈ A
○ reward : rt ∈ R(st, at)
○ policy : at ~ π(· | st)
○ transition : (st+1, rt+1) ~ P(· | st, at)
③ 사실상 거의 대부분의 문제 상황이 Markov decision process에 해당함
④ 최적화 해 V(s)의 존재성
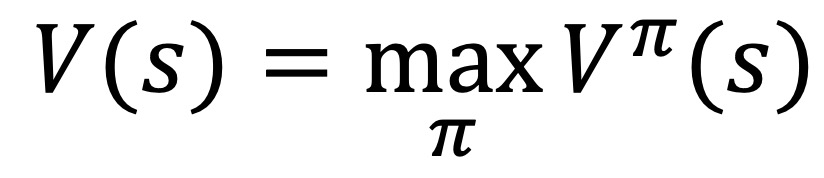
○ 전제 1. Markov property
○ 전제 2. stationary assumption
○ 전제 3. no distributional shift
⑵ 종류 1. Q-learning
① 정의 : 모든 state에 대하여 value function Vπ(s)를 학습하는 것
○ transition probability P(s' | s, a)는 알려져 있지 않음
○ reward function R(s, a)는 알려져 있지 않음
② 방법 1.
○ 모든 state / action pair의 추정량을 초기화 : Q̂(s, a) = 0
○ 초기 반복 scheme
○ 랜덤한 action a를 취함
○ 다음 상태 s'를 관찰하고 환경으로부터 R(s, a)를 받음
○ Q̂(s, a)를 업데이트
○ 후기 반복 scheme
○ a = arg maxa Q̂(s, a)를 취함
○ 다음 상태 s'를 관찰하고 환경으로부터 R(s, a)를 받음
○ Q̂(s, a)를 업데이트
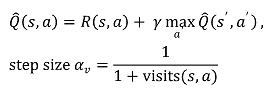
○ random restart
③ 방법 2. ε-greedy (epsilon greedy)
○ 모든 state / action pair의 추정량을 초기화 : Q̂(s, a) = 0
○ 반복 scheme
○ 1 - ε의 확률로 a = arg maxa Q̂(s, a)를 취하고, ε의 확률로 random action을 취함
○ 다음 상태 s'를 관찰하고 환경으로부터 R(s, a)를 받음
○ Q̂(s, a)를 업데이트
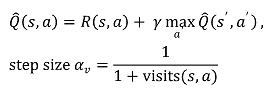
○ 후기 반복일 경우 random restart
④ DQN(deep Q-network)
○ 정의 : Q learning을 deep learning으로 구현한 것
○ 수많은 게임에 적용됨 : DQN on Atari 2600 (2013), AlphaGo (2016) 등
⑶ 종류 2. policy gradient
① 정의 : policy π(s)를 직접 학습하는 것
② 특징
○ Q-learning은 state가 continuous해도 되는 반면 action은 discrete해야 함
○ policy gradient는 action 및 state가 continuous해도 됨
③ 알고리즘
○ step 1. frame을 받음
○ step 2. P(action)을 얻기 위해 forward를 propagate함
○ step 3. P(action)으로부터 a를 샘플링
○ step 4. 게임의 나머지를 진행
○ step 5. 만약 게임에서 이기면 ∇θ 방향으로 진행
○ step 6. 만약 게임에서 지면 -∇θ 방향으로 진행
⑷ 기타 종류
① deep O-network (DON)
② A3C
③ genetic algorithm
④ SARSA
4. Markov chain Monte Carlo (MCMC) [목차]
⑴ 정의 : 복잡한 확률 분포를 따르는 Markov chain으로부터 샘플을 생성하기 위해 사용하는 방법
⑵ 종류 1. Metropolis-Hastings
① 현재 상태에서 새로운 후보 샘플을 생성 → 후보 샘플을 수락 또는 거절 → 수락될 때만 새로운 상태로 전환됨
⑶ 종류 2. Gibbs sampling
⑷ 종류 3. importance/rejection sampling
⑸ 종류 4. reversible jump MCMC
① 종류 1, 2와 같은 일반적인 MCMC는 고정된 차원의 매개변수 공간에서 확률 분포를 샘플링하는 알고리즘
② reversible jump MCMC는 가변 차원의 매개변수 공간에서 작동 : 샘플링 중에 매개변수의 차원이 동적으로 변함
입력: 2021.12.13 15:20
수정: 2024.10.08 22:43
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 27강. 기타 알고리즘 (0) | 2022.01.11 |
|---|---|
| 【알고리즘】 12-1강. DIP(Deep Image Prior) (0) | 2021.12.31 |
| 【알고리즘】 6강. 분류 알고리즘 (0) | 2021.12.11 |
| 【알고리즘】 23강. 베이지안 최적화와 MAB (0) | 2021.12.10 |
| 【알고리즘】 7강. 차원 축소 알고리즘 (0) | 2021.12.03 |



최근댓글