6강. 분류 알고리즘(classification algorithm)
추천글 : 【알고리즘】 알고리즘 목차
1. 개요 [본문]
2. 종류 1. linear classificer [본문]
3. 종류 2. K-nearest neighboring alrogithm [본문]
4. 종류 3. 결정 트리 [본문]
5. 종류 4. 베이스 분류기 [본문]
6. 종류 5. 도메인 적응 분류 [본문]
7. 종류 6. 딥러닝 기반 분류 [본문]
8. 기타 알고리즘[본문]
b. Calibrated Classification Model
1. 개요 [목차]
⑴ 정의
① y ~ X (단, | { y } | ＜ ∞ )
② supervised algorithm에 속함
⑵ calibrated classification model
2. 종류 1. linear classifier [목차]
⑴ 개요
① 비선형 회귀분석을 이용
② 단점 1. linear classifier는 클래스 별로 오직 하나의 템플릿만 학습할 수 있음
③ 단점 2. linear classifier는 decision boundary 중 오직 linear decision boundary만을 구현할 수 있음
④ (참고) 초평면(hyperplane) : 다중회귀를 나타낸 3D 이상의 차원의 표면
⑵ 1-1. SVM(서포트 벡터 머신, support vector machine)
① 개요
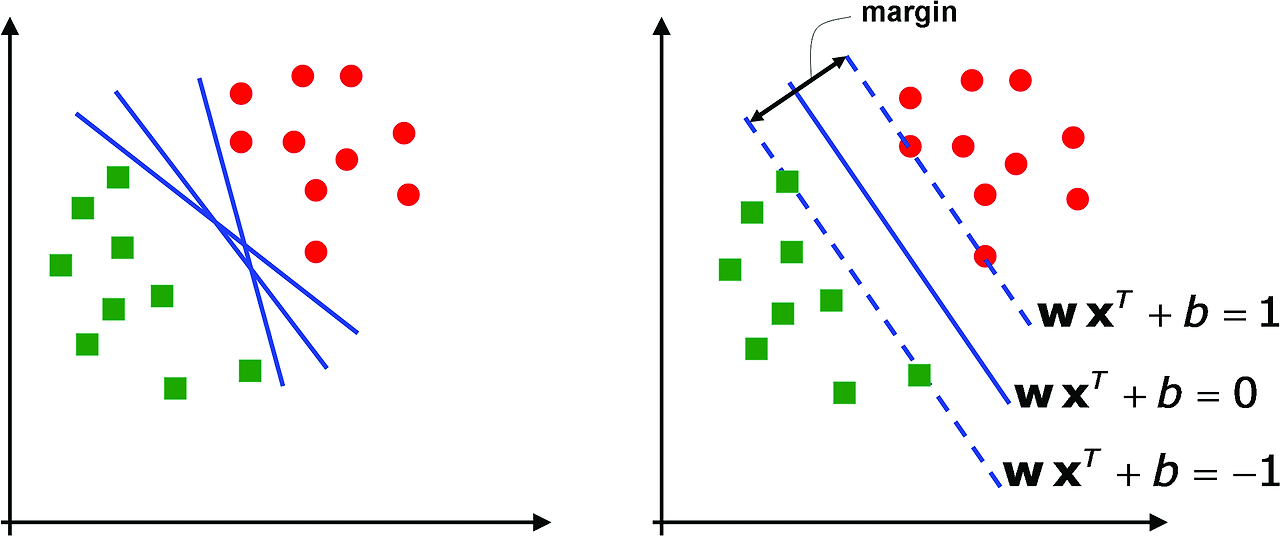
○ 정의 : 고차원 혹은 무한 차원의 공간에서 margin을 극대화하는 최적의 초평면(MMH, maximum margin hyperplane; 최대 마진 초평면)을 설정하여 점들을 두 종류로 분류하는 기법
Figure. 1. SVM과 초평면
○ 서포트 벡터가 여러 개일 수 있음 : 초평면을 여러 개로 설정하면 점들을 여러 집합으로 분류할 수 있음
○ 선형으로 분리가 불가능한 분류 문제에는 전차원 공간을 고차원 공간으로 매핑하여 분류가 가능함
○ 장점 : 자주 사용되던 방법 → 연구가 잘 돼 있음. 다른 모형보다 과대 적합(overfitting)에 강함. 정확성이 뛰어남
○ 단점 : 테스트 셋을 제공해야 하는 지도학습(supervised learning). 다른 모형에 비해 속도가 느림
② 수식화
Figure. 2. SVM 수식화
○ 마지막 수식의 의의 : 최적화 알고리즘을 적용하기 용이하고 커널을 적용하여 선형으로 분리가 불가능한 분류 문제에 적용 가능
○ slack variable이라고도 하는 ξi = 1 - yi (wxi + b)를 도입하여 제한조건을 위배하는 일부 데이터포인트를 허용함
③ SVM에서 사용되는 커널
○ 선형 커널 : 기본 유형의 커널이며 1차원이고 다른 함수보다 빠름
○ 다항 커널 : 선형 커널의 일반화된 공식이며, 효과성과 정확도 측면에서 효율이 적어 선호하지 않음
○ 가우시안 커널 : 일반적으로 사용하는 커널이며, 데이터에 대한 사전 지식이 없는 경우 활용됨
○ 가우시안 RBF 커널 : 가장 많이 사용하는 커널이며, 비선형 데이터가 있는 경우에 일반적으로 활용됨. 다음 수식에서 벡터 ℓ은 랜드마크 (예 : 데이터 포인트의 중심)
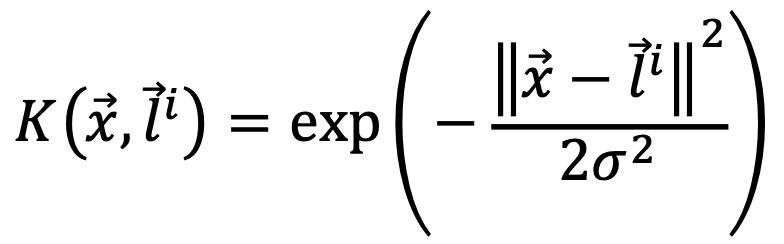
○ 시그모이드 커널 : 인공신경망에서 선호도는 커널로서 인공신경망의 다층 퍼셉트론 모델과 유사함
④ R에서의 구현
## data
print(head(iris))
## training
library(e1071)
train <- sample(1:150, 100)
sv <- svm(Species ~., data= iris, subset = train, type = "C-classification")
## testing
pred = predict(sv, iris[-train, ])
print(head(pred))
## review
tt <- table(iris$Species[-train], pred)
print(tt) # confusion matrix
⑶ 1-2. nu-SVM
⑷ 1-3. probability regression model : LPM, probit, logit 등
① R 코드
## R code
# Train the logistic regression model
model <- glm(species ~ ., data = x_train, family = binomial())
# Predict probabilities
prob_estimates <- predict(model, x_test, type = "response")
3. 종류 2. K-nearest neighboring algorithm (K-NN) [목차]
⑴ 개요
① K개의 가장 가까운 training data point들로부터 주어진 test data point를 labeling하는 방법
② 예시 : 유튜브 추천 시스템
③ 5차원을 넘어가면 잘 작동을 하지 않음
④ K-NN은 SVM보다 시간 복잡도가 큼
⑵ step 1. 데이터 로딩 및 아키텍처 설계
import numpy as np
import tensorflow as tf
class NearestNeighbor(object):
...
(Xtr, Ytr), (Xte, Yte) = tf.keras.datasets.mnist.load_data()
print(Xtr.shape) # (60000, 28, 28)
print(Ytr.shape) # (60000,)
print(Xte.shape) # (10000, 28, 28)
print(Yte.shape) # (10000,)
Xtr_rows = Xtr.reshape(Xtr.shape[0], 28*28)
Xte_rows = Xte.reshape(Xte.shape[0], 28*28)
print(Xtr_rows.shape) # (60000, 784)
print(Xte_rows.shape) # (10000, 784)
nn = NearestNeighbor()
nn.train(Xtr_rows, Ytr)
Yte_predict = nn.predict(Xte_rows, 'L2')
print ('accuracy: %f' + str(np.mean(Yte_predict == Yte)) )
# L1 : accuracy = 47.29%
# L2 : accuracy = 27.24%
# dot : accuracy = 9.9%
⑶ step 2. NN 클래스 설계
class NearestNeighbor(object):
def __init__(self):
pass
def train(self, X, Y):
self.Xtr = X
self.Ytr = Y
def predict(self, X, dist_metric='L2'):
num_test = X.shape[0]
Ypred = np.zeros(num_test, dtype = self.Ytr.dtype)
for i in range(num_test):
if dist_metric=='L1': ## L1 distance
distances = np.sum(np.abs(self.Xtr - X[i, :]), axis = 1)
elif dist_metric=='L2': ## L2 distance
distances = np.sum(np.square(self.Xtr - X[i, :]), axis = 1)
elif dist_metric=='dot': ## dot distance
distances = np.dot(self.Xtr, X[i, :])
min_index = np.argmin(distances)
Ypred[i] = self.Ytr[min_index]
if i%100 == 0:
print(i)
return Ypred
① train 단계는 데이터를 저장하는 단계에 불과함
② 요인 1. 거리 함수의 설계
○ 거리 함수(distance function, metric) : 거리를 정의
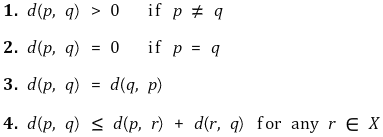
○ 1-1. L1 distance
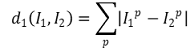
○ 1-2. L2 distance : 피타고라스 정리를 이용한 유클리드 거리 (표준)
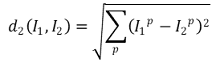
○ 1-3. p-norm
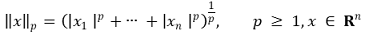
○ 1-4. dot product
○ 1-5. KL 거리(Kullback-Leibler divergence)
○ 1-6. 기타 거리함수
○ L1 distance와 L2 distance에 의한 결과는 유사함 : L1 38.6 %, L2 35.4 %
③ 요인 2. 1-NN vs k-NN
○ k가 증가함에 따라 각 영역의 가장자리가 부드러워짐
○ k가 너무 작으면 robust하지 않아 outlier나 노이즈에 반응하여 labeling하는 문제가 있음
○ k가 증가함에 따라 ambiguous한 region이 나타남
⑷ step 3. hyperparameter tuning : 여러 k 값을 시도해 보고 가장 좋은 결과를 내는 k 값을 고르면 됨
Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # keep last 59,000 for train
Ytr = Ytr[1000:]
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:
nn = NearestNeighbor()
nn.train(Xtr_rows, Ytr)
Yval_predict = nn.predict(Xval_rows, k = k)
acc = np.mean(Yval_predict == Yval)
print 'accuracy: %f' % (acc,)
validation_accuracies.append((k, acc))
⑸ step 4. 개선
① 단점
○ 픽셀 레벨에서 KNN을 쓰면 그 유사성 개념이 진실한 유사성이라 할 수 없어 퍼포먼스가 뛰어나지 않음
○ test time이 매우 느림
○ K 값이 작으면 아웃라이어 데이터에 취약해짐
○ 차원의 저주 : 차원이 증가할수록 example들 간의 같은 거리를 유지하기 위한 데이터 수가 기하학적으로 증가. 따라서 example들 간에 너무 sparse하면 너무 대충 분류하게 되는 결과가 초래됨
② 개선사항
○ 데이터의 정규화 : 평균이 0, 표준편차가 1이 되도록 하는 과정
○ 차원 축소 : PCA, NCA, random projection 등
○ cross-validation : computationally expensive. 3-fold, 5-fold, 10-fold cross-validation이 자주 사용됨
○ approximate nearest neighboring : 정확성은 감소하고 속도는 빨라짐 (예 : FLANN)
③ 위와 같은 개선사항에도 불구하고 실제로 거의 사용되지 않음
⑹ 2-1. mutual nearest neighboring algorithm
⑺ K-NN과 K-평균 군집화의 비교
| 항목 | K-NN | K-평균 군집화 |
| 유형 | 지도학습 | 비지도학습 |
| k의 의미 | 근접한 이웃의 수 | 클러스터의 수 |
| 최적화 기법 | cross validation, 혼동행렬 | 엘보우, 실루엣 기법 |
| 활용 | 분류 | 클러스터링 |
Table. 1. K-NN과 K-평균 군집화의 비교
4. 종류 3. 결정 트리(decision tree) [목차]
⑴ 개요
① 주어진 입력값에 대하여 출력값을 예측하는 모형으로 단일나무와 회귀 나무 모형이 있음
② 분석의 대상을 분류함수를 활용하여 의사결정 규칙으로 이루어진 나무 모양으로 그리는 기법
③ 부모 마디의 순소도에 비해서 자식 마디들의 순수도가 증가
④ 계산 결과가 의사결정나무에 직접적으로 나타남
⑤ 연속형 변수를 비연속적인 값으로 취급하기 때문에 분리의 경계점 근방에서 예측 오류가 큰 단점이 있음
⑵ 3-1. 단순한 결정 트리
① 개요
○ 장점 1. 주어진 데이터에 대한 표현력(expressivity)이 좋음
○ 장점 2. 해석 가능하고 빠름
○ 장점 3. 다음 데이터를 쉽게 처리할 수 있음 : categorical, mixed data, missing data, multiple classes
○ 단점 1. overfitting 가능성 : 즉, outlier에 취약 (해결방법 : tree pruning)
○ 단점 2. 트리가 너무 깊어짐 (해결방법 : tree pruning)
○ 단점 3. 연속적인 수치형 데이터를 다루기 곤란함
② 용어
○ root node
○ internal node (node) : attribute에 대한 조건문을 형성하는 노드
○ branching : internal node에서 갈라져 나온 가지로 attribute value에 의해 결정
○ leaf node (terminal node, decision node) : 아웃풋 (class assignment)
③ 결정트리의 학습
○ 조건 1. 너무 크지도 작지도 않을 것
○ 조건 2. 오캄의 면도날(Occam's Razor) 이론 : the simplest is the best
○ 조건 3. complexity는 depth에 의존함
○ 가장 작고 심플한 결정 트리를 학습시키는 것은 NP complete 문제 (Hyafil & Rivest (1976))
○ greedy heurisitic으로 결정 트리를 학습시킬 수 있음
### BuildTree (D): Greedy training of a decision tree ###
# Input: A data set D = (X, Y).
# Output: A decision tree.
if LeafCondition(D) then
fn = FindBestPrediction(D)
else
jn, tn = FindBestSplid(D)
DL = {(x(i), y(i)) : x(i)_(jn) < tn} and
DR = {(x(i), y(i)) : x(i)_(jn) ≥ tn}
leftChild = BuildTree(DL)
rightChild = BuildTree(DR)
end if
○ 단계 1. score all splits
○ 단계 2. information gain이 최대가 되는 조건을 greedy하게 찾음
○ 단계 3. 그 조건으로 데이터셋을 구분하고 각 서브트리에서 단계 1, 단계 2를 recursive하게 수행
○ 단계 4. stopping criteria
④ R 코드
## R code
library(rpart)
# Train the decision tree model
model <- rpart(species ~ ., data = x_train, method = "class")
# Predict probabilities
prob_estimates <- predict(model, x_test)
⑤ 응용 1. pruning
⑥ 응용 2. information gain ratio
⑶ 3-2. bagging (bootstrap aggregation)
① 정의 : 복원추출을 하여 얻은 서로 다른 데이터셋에 대한 분류 결과를 투표로 결정하는 것
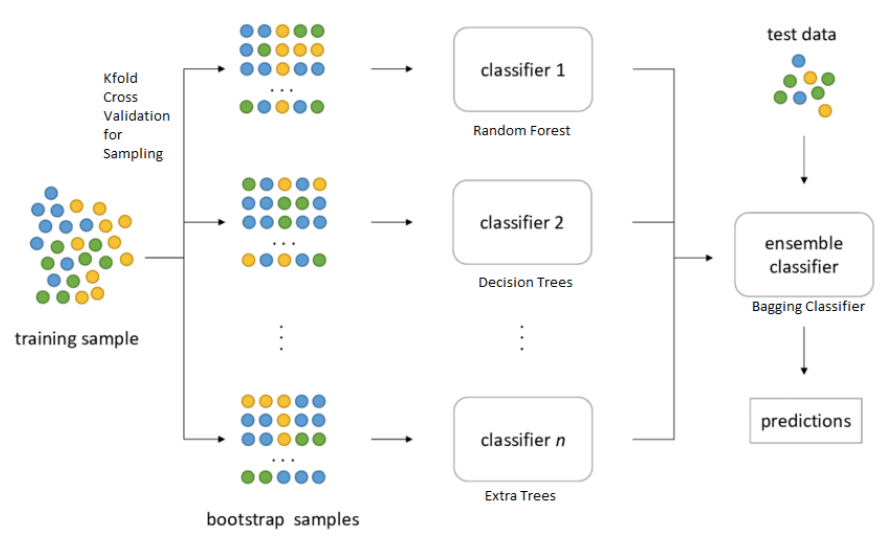
② 부트스트랩 : 한 번 시작되면 알아서 진행되는 일련의 과정으로 결정 트리에 국한하지 않음
③ 장점 1. 트리와 같은 불안정한 과정의 분산을 줄여 예측력을 높임
④ 장점 2. 결정 트리의 경계를 smoothing 시킴
⑷ 3-3. 랜덤 포레스트(random forest)
① 정의 : 각 sub-dataset에서 m개의 feature를 뽑아 bagging에 활용하는 것
○ 예시 : 매번 학습할 때 도시, 인구수, 소득평균, 신생아수, 신혼가정 수 등 여러 피쳐 중 랜덤한 정보만 가져와 학습
② 특징 1. de-correlating : 일부 feature만을 사용함으로써 각 sub-dataset의 개성을 높임
③ 특징 2. 각 sub-dataset에서 뽑히지 않은 나머지 데이터셋은 out-of-sample error를 validation할 때 사용할 수 있음
④ 퍼포먼스 : random forest ＞ bagging ＞ decision tree
○ 정확도 : Adaboost와 같거나 높음
○ robustness : outlier와 노이즈에 대해 상대적으로 robust함
○ 속도 : bagging, bossting보다 빠름
○ 간단하고 쉽게 parallelized될 수 있음
○ 현재 분류 알고리즘 연구에서 가장 퍼포먼스가 뛰어남
⑤ R 코드
## R code
library(randomForest)
# Train the random forest model
model <- randomForest(species ~ ., data = x_train)
# Predict probabilities
prob_estimates <- predict(model, x_test, type = "prob")
⑸ 3-4. C4.5와 C5.0
① 호주의 연구원 J. Ross Quinlan에 의하여 개발
② 초기 버전은 ID 3(iterative dichotomizer 3)로 1986년에 개발
③ 가지치기를 사용할 때 학습자료를 사용
④ 종속변수가 이산형이며, 불순도의 척도로 엔트로피 지수(entropy index) 사용
⑹ 3-5. CHAID
① 카이제곱 통계량을 사용하고, 분리 방법은 다지 분리를 사용하는 의사결정나무 알고리즘
⑺ 3-6. CART(classification and regression tree)
① 각 독립변수를 이분화하는 과정을 반복하여 이진 트리 형태를 형성함으로써 분류를 수행하는 방법
⑻ 3-7. AdaBoost
⑼ 3-8. QUEST
⑽ 3-9. K-D tree
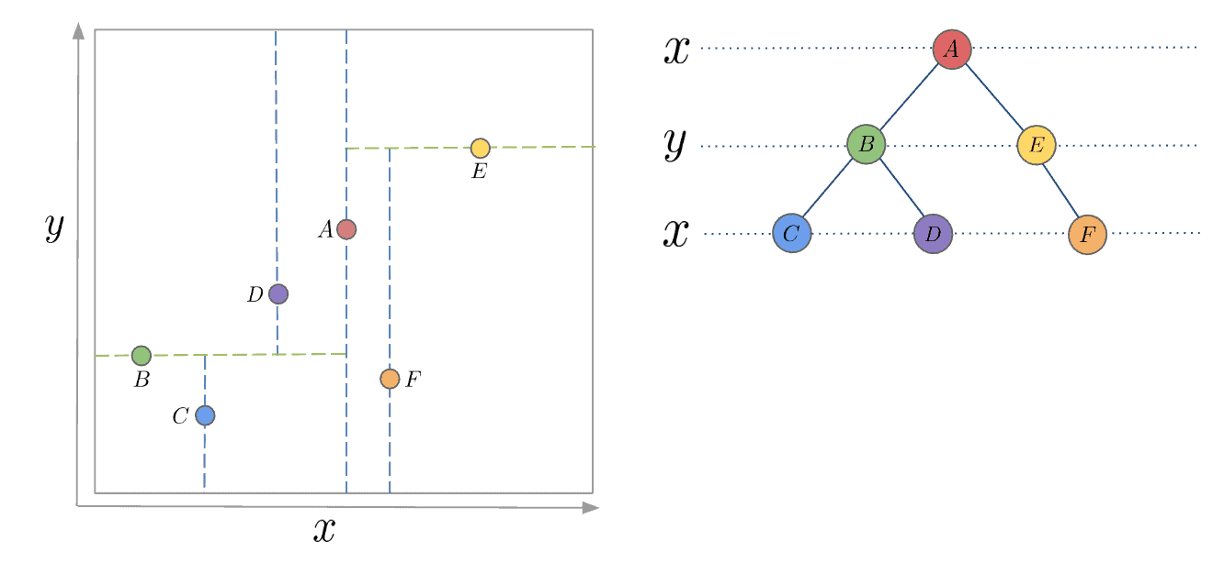
① 정의 : k차원 공간의 점들을 구조화하는 공간 분할 자료 구조
② K-D tree의 구성 : 각 분할별로 x축 중앙점, y축 중앙점을 차례로 찾으면서 공간을 분할함
Figure. 4. K-D tree의 구성
③ K-D tree를 이용한 최단 거리 계산
○ step 1. 루트 노드에서 시작하여 탐색을 진행
○ step 2. 각 분할 축(axis)에 따라 coords가 속할 수 있는 자식 노드를 선택하여 하위 노드로 내려감
○ step 3. step 2를 반복하여 해당 좌표가 속할 가능성이 높은 리프 노드에 도달
○ step 4. 리프 노드에 포함된 점들과 coords 사이의 유클리드 거리(Euclidean distance)를 계산
○ step 5. 리프 노드에서 얻은 최단 거리를 기준으로, 상위 노드 및 형제 노드가 더 가까운 이웃을 포함할 가능성을 평가함. 형제 노드가 탐색할 가치가 있으면 해당 노드에서 거리 계산을 반복
○ step 6. K-D tree의 공간 분할 특성을 이용하여, 탐색할 필요 없는 노드는 건너뜀 (pruning)
5. 종류 4. 베이스 분류기 [목차]
⑴ Naïve Bayes classifier
① 개요
○ 데이터에서 변수들에 대한 조건부 독립을 가정하는 알고리즘
○ 클래스에 대한 사전정보와 데이터로부터 추출된 정보를 결합하고 베이즈 정리를 이용하여 어떤 데이터가 특정 클래스에 속하는지를 분류하는 알고리즘
○ 텍스트 분류에서 문서를 여러 범주(예 : 스팸, 경제, 스포츠 등) 중 하나로 판단하는 문제에 대한 솔루션으로 사용될 수 있음
② 수식화
○ 전제 : K개의 클래스 C1, C2, ···, CK가 존재함
○ 목적 : 여러 피처로 구성된 새로운 샘플 x = (x1, ···, xN)이 주어져 있을 때 어떤 클래스에 속하는지 결정
○ 수식화 : MLE(maximum likelihood estimation)와 유사
③ 한계
○ 조건부 독립 불성립 : 만약 피처 간의 유의한 상관관계가 존재하면 (e.g., 나이와 심장병 전력), 관련 있는 변수들이 여러 번 곱해지므로 이들의 효과가 과대평가됨
○ 관련 없는 피처들의 영향을 배제할 수 없음
○ 해결 방법 : PCR, mRMR 등을 써서 필요 없는 변수는 버리고 필요한 변수는 최소로 남기면 위 한계들을 해소할 수 있음
⑵ Bayesian network
6. 종류 5. 도메인 적응 분류(domain adaptation classification) [목차]
⑴ 개요
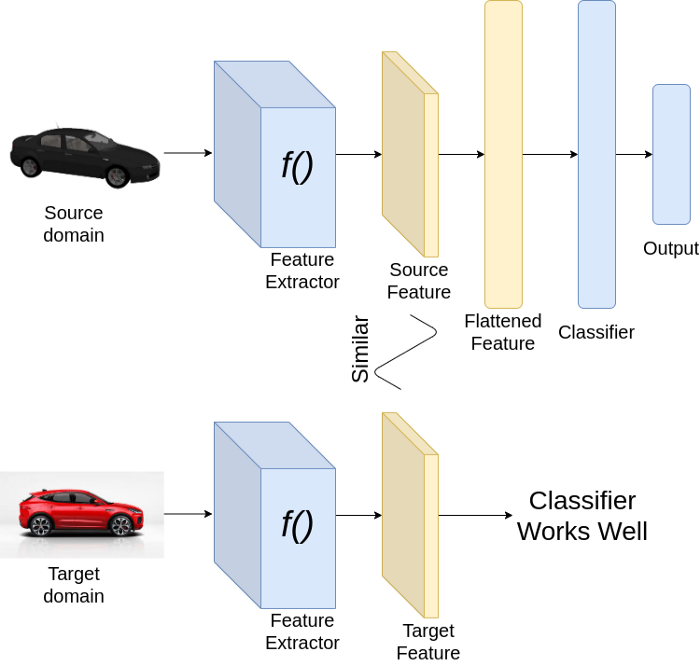
① 정의 : 한 도메인에서 universal knowledge를 얻어서 다른 도메인에 적용하는 것
② 한 도메인 : source domain, tangential domain 등으로 불림. 데이터셋 크기가 큼
③ 다른 도메인 : target domain, specific domain 등으로 불림. 데이터셋 크기가 작음
④ 일반화(generalization)와의 차이점
○ 도메인 적응 분류 : source와 target의 형식, 자료구조 등이 다름
○ 일반화 : source와 target의 형식, 자료구조 등이 동일
⑵ 종류
① UDA(unsupervised domain adaptation) : target domain에 label이 없는 경우
○ 즉, source domain에서 얻은 feature를 target domain에 바로 적용하는 구조
② SSL(supervised domain adaptation) : target domain에 label이 있는 경우
③ SSDA(semi-supervised domain adaptation) : target domain이 label이 일부만 있는 경우
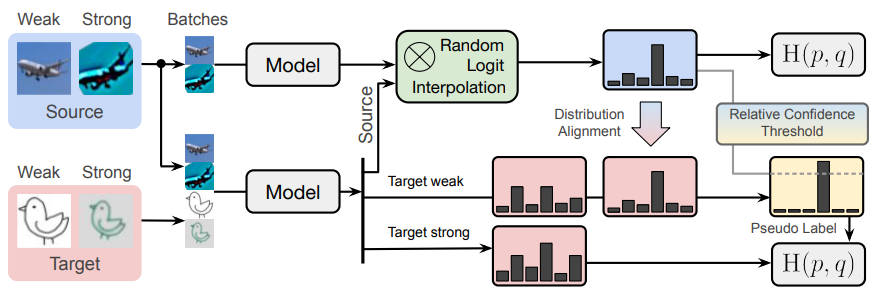
○ 과정 1. augmentation
○ 과정 2. random logit interpolation
○ 과정 3. distribution alignment
○ 과정 4. relative confidence threshold
○ 과정 5. loss function
○ SOTA(state-of-the-art)인 이유 : trade-off가 있기 때문으로 링크 내 'motivation' 부분에서 확인 가능
⑶ 목적함수
① domain 간 discrepancy를 줄이는 것을 목적으로 함
② discrepancy 종류
○ MMD(maximum mean discrepancy)
○ DANN(domain adversarial neural network)
○ MCD(maximum classifier discrepency)
⑷ 응용
① divergence domain adaptation
② adversarial domain adaptation
○ 생성적 대립신경망(generative adversarial network, GAN)
○ 정의 : 서로 경쟁하면서 학습하는 두 개의 AI 시스템 (game learning)
○ 생성모델 : 기존 데이터의 다양한 특징을 바탕으로 학습한 지식을 활용해 새로운 데이터를 생성
○ 판별모델 : 생성된 새로운 데이터가 기존 데이터와 얼마나 유사한지 평가
○ 생성모델과 판별모델 사이에 아이디어가 오가면서 실제와 가까운 결과를 자동으로 만들어냄
③ reconstruction domain adaptation
7. 종류 6. 딥러닝 기반 분류(deep-learning-based classification) [목차]
⑵ 6-1. 1D CNN
8. 기타 알고리즘 [목차]
⑴ Faiss
① 2023년 Meta에서 개발한 유사도 기반 탐색 및 dense vector 클러스터링 알고리즘
② 고속 검색 알고리즘 : nearest neighbor와 k-th nearest neighbor를 얻을 수 있음
③ 한번에 여러 벡터를 검색할 수 있음 (batch processing)
④ 정확도와 속도 간에 트레이드 오프가 존재함
⑤ 유클리드 거리를 최소화 하는 검색이 아닌 maximum inner product가 최대로 되는 방식으로 계산
⑥ 주어진 radius에 포함되는 모든 element들을 반환
입력: 2021.12.12 11:37
수정: 2024.12.30 17:09
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 12-1강. DIP(Deep Image Prior) (0) | 2021.12.31 |
|---|---|
| 【알고리즘】 11강. 강화학습 (0) | 2021.12.13 |
| 【알고리즘】 23강. 베이지안 최적화와 MAB (0) | 2021.12.10 |
| 【알고리즘】 7강. 차원 축소 알고리즘 (0) | 2021.12.03 |
| 【알고리즘】 16강. CNN 신경망 (0) | 2021.11.21 |
최근댓글