7강. 차원 축소 알고리즘(dimension reduction algorithm)
추천글 : 【알고리즘】 알고리즘 목차
1. 개요 [본문]
2. 종류 1. 주성분 분석 (PCA) [본문]
3. 종류 2. SNE, symmetric-SNE, tSNE [본문]
4. 종류 3. UMAP [본문]
5. 종류 4. SVD [본문]
6. 종류 5. ICA [본문]
7. 종류 6. PPCA [본문]
8. 종류 7. CCA [본문]
9. 기타 [본문]
b. UMAP
1. 개요 [목차]
⑴ 차원 축소의 정의
① 고차원 데이터 X(1), ···, X(n) ∈ ℝp의 데이터가 주어져 있을 때,
② 적절한 subspace V ⊂ ℝp (단, dim(V) = k)를 찾고,
③ X의 V로의 투상(projection) X̃을 계산하는 것
④ unsupervised algorithm에 속함
⑵ 특징
① 정보 유지
② 모델 학습의 용이 : 머신러닝에 있어 더 적은 파라미터를 요하므로 더 빠르고 연산량이 적음
③ 결과 해석의 용이 : 주어진 고차원 데이터의 시각화
④ 노이즈 감소
⑤ 주어진 데이터의 진정한 dimensionality를 확인할 수도 있음
⑶ 방법
① 변수 선택(feature selection)
○ 가지고 있는 변수들 중 중요한 변수 몇 개만 고르고 나머지는 버리는 방법
○ 상관계수가 높거나 분산팽창지수(VIF, variance inflation factor)가 높은 변수 중 하나를 선택
② 변수 추출(feature extraction)
○ 모든 변수를 조합하여 이 데이터를 잘 표현할 수 있는 중요 성분을 가진 새로운 변수를 도출
○ 기존 변수를 조합해 새로운 변수를 만드는 기법
2. 종류 1. 주성분 분석(PCA, principal component analysis) [목차]
⑴ 개요
① 정의 : correlated variable을 orthogonal variable로 바꾸는 변환하는 차원 축소 기법
② 즉, 유의미한 몇 개의 진정한 직표좌표계만을 남기는 차원 축소 기법
③ orthogonal varible을 주성분이라고 하며, 주성분이 원본만큼 많은 정보량을 포함할 때 사용할 수 있음
④ 주어진 차원과 데이터의 진정한 차원이 다를 수 있다는 문제의식에서 출발
⑤ Pearson에 의해 1901년에 최초로 소개됨
⑥ 주성분 분석은 subspace (원점 지남)이 아니라 affine space에서도 정의할 수 있음
⑦ 즉, 평균값에 대해 정규화한 뒤 subspace에 대한 주성분 분석을 하면 됨
⑧ 주성분 분석은 주어진 데이터의 multivariate normality를 요하지 않음
⑨ 데이터가 선형으로 분포할 때 쓸 수 있음
⑩ whitening : 각 피처를 표준화(standardization) 할 때에도 주성분 방향으로 표준화를 하면 더 좋음
⑵ 전제
① 데이터가 속한 공간의 기저를 각각 e1, ···, ep로 표시 (단, 기저집합이 직교집합일 필요는 없음)
○ e1, ···, ep는 주어진 차원을 나타내는 기저라고 할 수 있음 (단, 직교할 필요는 없음)
② 목표 : 다음과 같은 subspace의 직교 기저 Z1, ···, Zk를 찾아내는 것 (단, k < n) (일반적인 unsupervised problem 셋팅)
○ Z1, ···, Zk는 데이터의 진정한 차원을 나타내는 기저라고 할 수 있음

③ random vector
○ X는 특정 데이터 포인트를 나타냄 : x1, ···, xn은 각 성분
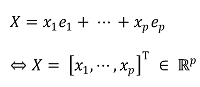
④ mean vector : population mean이라고도 함
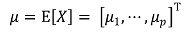
⑤ variance-covariance matrix
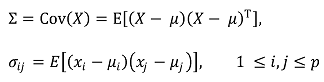
⑥ unbiased sample variance-covariance matrix : design matrix X, center matrix Xc에 대하여,
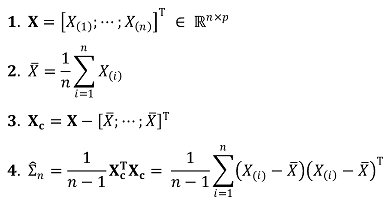
○ population variance-covariance matrix가 알려져 있지 않으면 사용함
○ X ∈ ℝn×p이므로 XTX ∈ ℝp×n × ℝn×p = ℝp×p
⑦ 목표 직교 기저의 표현
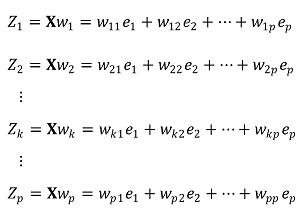
○ Zk := kth PC ∈ ℝp×1
⑧ 목표 직교 기저의 특징 : 선형대수학 개념으로 쉽게 유도됨
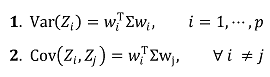
○ Var, Cov 등은 분산에 대한 특정 값이므로 ℝ1x1에 속함
○ variance-covariance matrix와 헷갈리지 말 것
⑶ 주성분 분석 문제 정의
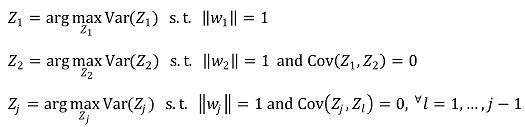
⑷ 주성분 분석 문제 풀이
① 방법 1. ∑의 eigen-decomposition
○ 단계 1. 데이터의 구성과 중심화
○ X ∈ ℝn×d : n개의 샘플과 d개의 피처를 가지는 데이터 행렬
○ 데이터 행렬 X를 중심화(centering) : Xc = X - μ (단, μ ∈ ℝd는 각 열의 평균들을 모아놓은 벡터)
○ 단계 2. 공분산 행렬 계산
○ 중심화된 데이터로부터 샘플 공분산 행렬 C ∈ ℝd×d를 계산
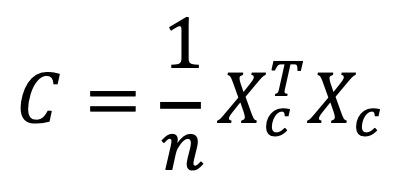
○ 주어진 샘플이 모집단 전체이기 때문에 population mean이 알려져 있어 샘플 공분산을 계산할 때 n−1 대신 n으로 나눔
○ 단계 3. eigen-decomposition 수행
○ 공분산 행렬 C에 대해 고유값(eigenvalue)과 고유벡터(eigenvector)를 계산 : C · pi = λi · pi
○ 여기서 λi는 고유값, pi ∈ ℝd는 고유벡터
○ 참고로, 대칭행렬인 C는 언제나 직교 대각화가 가능함 (∵ spectral theorem)
○ 단계 4. 데이터 변환
○ P = [p1, p2, ⋯, pd] ∈ ℝd×d : 고유벡터를 열벡터로 가지는 행렬
○ 데이터를 새로운 좌표계로 변환 : Y = XcP (단, Y ∈ ℝn×d는 변환된 데이터 행렬)
○ 단계 5. 공분산 행렬의 대각화
○ 변환된 데이터 Y의 공분산 행렬은 대각행렬이 됨
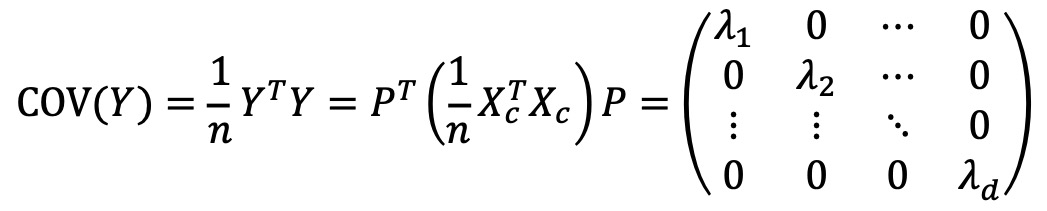
○ 단계 6. 주성분 선택 및 차원 축소
○ 고유값 λi가 큰 순서대로 k개의 주성분(고유벡터)을 선택하여 차원을 축소 : Yk = XcPk (단, Pk ∈ ℝd×k, Yk ∈ ℝn×k)
○ 주성분의 개수를 특정하지 않고 특정 임계값 η보다 작은 고유값을 제거하기도 함
○ 결론 1. d번째 주성분 PCd = d 번째로 큰 고유값(eigen value)에 대한 고유벡터
○ 결론 2. 고유값이 같은 고유벡터의 의미 : 대응하는 주성분의 크기가 같음
② 방법 2. center matrix Xc의 SVD(singular value decomposition) : 현재 PCA 알고리즘에서 표준 방법으로 채택
○ 단계 1. 데이터를 중심으로 이동하여 centered data Xc를 획득
○ 단계 2. C = (1/n) XcTXc = ∑ (covariance matrix)를 정의
○ 단계 3. C는 symmetric이므로 직교대각화가 가능함 : C = VDVT와 같이 표현됨 (단, 이때 V는 Xc = U∑VT에서의 V와 동일함)
○ 단계 4. V의 1, 2, ···번째 열벡터는 1, 2, ···번째로 큰 고유치와 대응하는 고유벡터이자 주성분
③ 방법 3. 등식 제약 하 라그랑주 승수법(Lagrange multiplier)
⑸ 축의 개수 결정
① 방법 1. fraction of total variance에 대한 scree plot
○ fraction of total variance의 정의
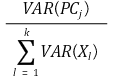
○ 도식화
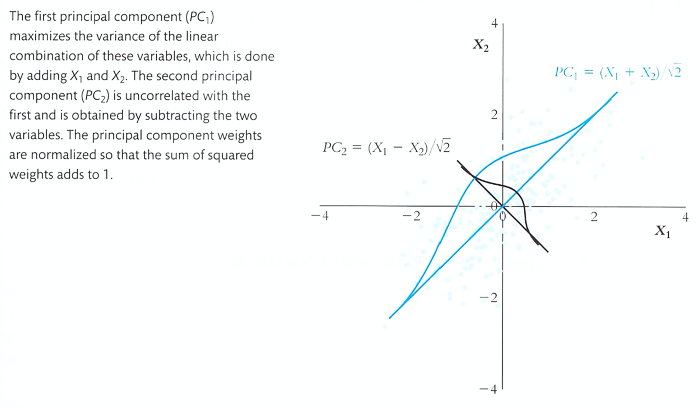
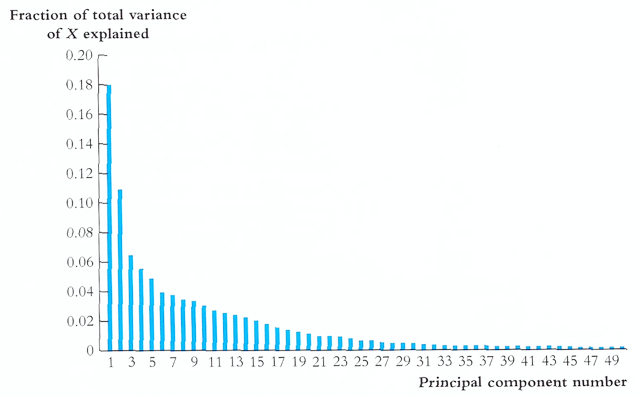
Figure. 2. scree plot : 각 성분 PC들이 설명하는 분산의 양을 표시
② 방법 2. eigen value에 대한 scree plot
③ 방법 3. in-sample 10-fold cross validation을 통해 MSPE를 최소로 하는 축의 개수 p 결정
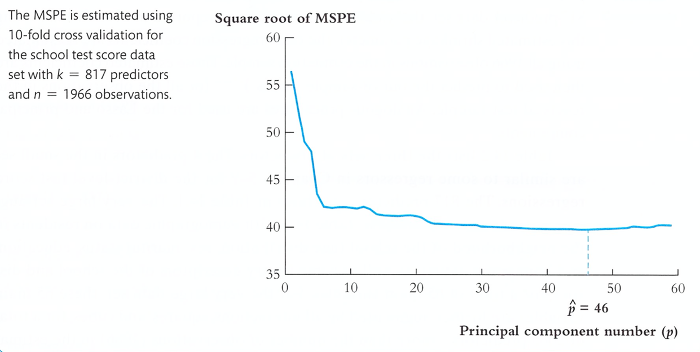
④ 나머지 축에 대한 정보를 잃어버리므로 PCA 알고리즘은 lossy compression algorithm의 기능을 수행함
⑹ 파이썬 코드 예제
import numpy as np
import matplotlib as mpl
mpl.use('Agg')
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
from ipywidgets import interact
%matplotlib inline
from sklearn.datasets import fetch_openml
def normalize(X):
mu = np.mean(X, axis=0)
std = np.std(X, axis=0)
std_filled = std.copy()
std_filled[std==0] = 1.
Xbar = ((X-mu)/std_filled)
return Xbar, mu, std
def eig(S):
eigvals, eigvecs = np.linalg.eig(S)
k = np.argsort(eigvals)[::-1]
return eigvals[k], eigvecs[:,k]
def projection_matrix(B):
return (B @ np.linalg.inv(B.T @ B) @ B.T)
def PCA(X, num_components=2):
# reconstruction
S = 1.0/len(X) * np.dot(X.T, X)
eig_vals, eig_vecs = eig(S)
eig_vals, eig_vecs = eig_vals[:num_components], eig_vecs[:, :num_components]
B = np.real(eig_vecs)
reconst = (projection_matrix(B) @ X.T)
return reconst.T
def PC_coords(X, num_components=2):
# low-dimensional projection
S = 1.0/len(X) * np.dot(X.T, X)
eig_vals, eig_vecs = eig(S)
eig_vals, eig_vecs = eig_vals[:num_components], eig_vecs[:, :num_components]
B = np.real(eig_vecs)
Xpca = X@B
return Xpca
images, labels = fetch_openml("mnist_784", version=1, return_X_y=True, as_frame=False)
labels=np.stack(labels).astype(None)
X = (images.reshape(-1, 28 * 28)) / 255.
subset_X = X[labels == 3]
Xbar, mu, std = normalize(subset_X)
num_components=2
X = Xbar
S = 1.0/len(X) * np.dot(X.T, X)
eig_vals, eig_vecs = eig(S)
eig_vals, eig_vecs = eig_vals[:num_components], eig_vecs[:, :num_components]
print(eig_vecs)
num_component = 2
reconst = PCA(Xbar, num_component)
reconstructions = reconst * std + mu # "unnormalize" the reconstructed image
⑺ PCA의 발전
① kernel PCA : 커널을 이용. 주어진 데이터를 고차원으로 늘릴 수도 있고, projection을 통해 저차원으로 축소할 수도 있음
② MDS(multidimensional scaling)
③ SNE, t-SNE
3. 종류 2. SNE, symmetric-SNE, tSNE [목차]
⑴ 확률 개념을 도입하여 MDS의 문제점을 해결
⑵ 특징 1. 데이터에서 지역 인접성(local neighborhoods)을 보존하려고 시도하는 차원 축소 알고리즘
① 엄청 먼 데이터 포인트는 고려하지 않는 local metric
⑶ 특징 2. 비선형적이며 비결정적
5. 종류 4. 특이값 분해(SVD, singular value decomposition) [목차]
⑴ M × N 차원의 행렬 데이터에서 특이값을 추출하고 이를 통해 주어진 데이터의 차원을 축소하는 기법
⑵ 수식화
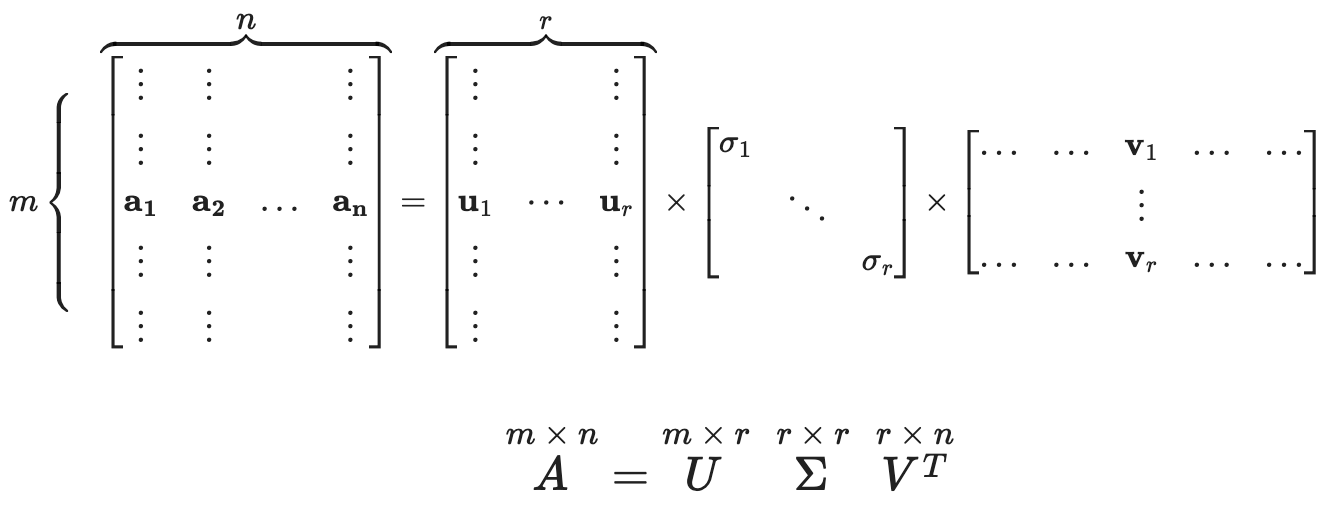
① 요약 : 만약 A가 계수(rank)가 r인 m × n 행렬이라면, 다음 조건을 만족하는 ℝm×m 행렬 U와 ℝn×n 행렬 V가 존재
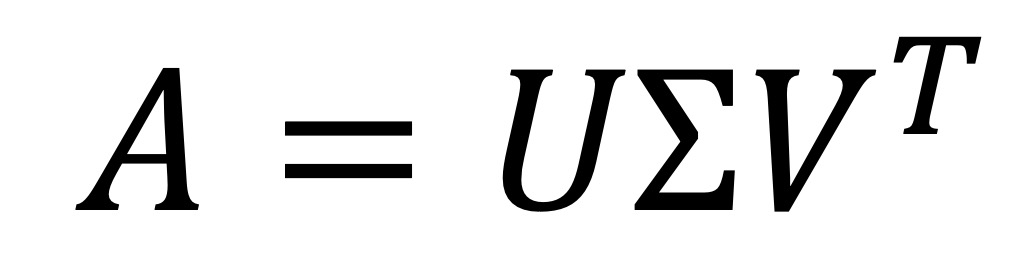
○ 단, U와 V는 orthonormal matrix
○ U의 각 열과 그에 대응하는 V의 각 열의 부호를 바꿔도 위 식이 성립하므로 SVD는 유일하게 결정되지 않음
○ 행렬 ∑ : 대각선이 r개의 nonzero singular value (> 0)인 m × n 행렬
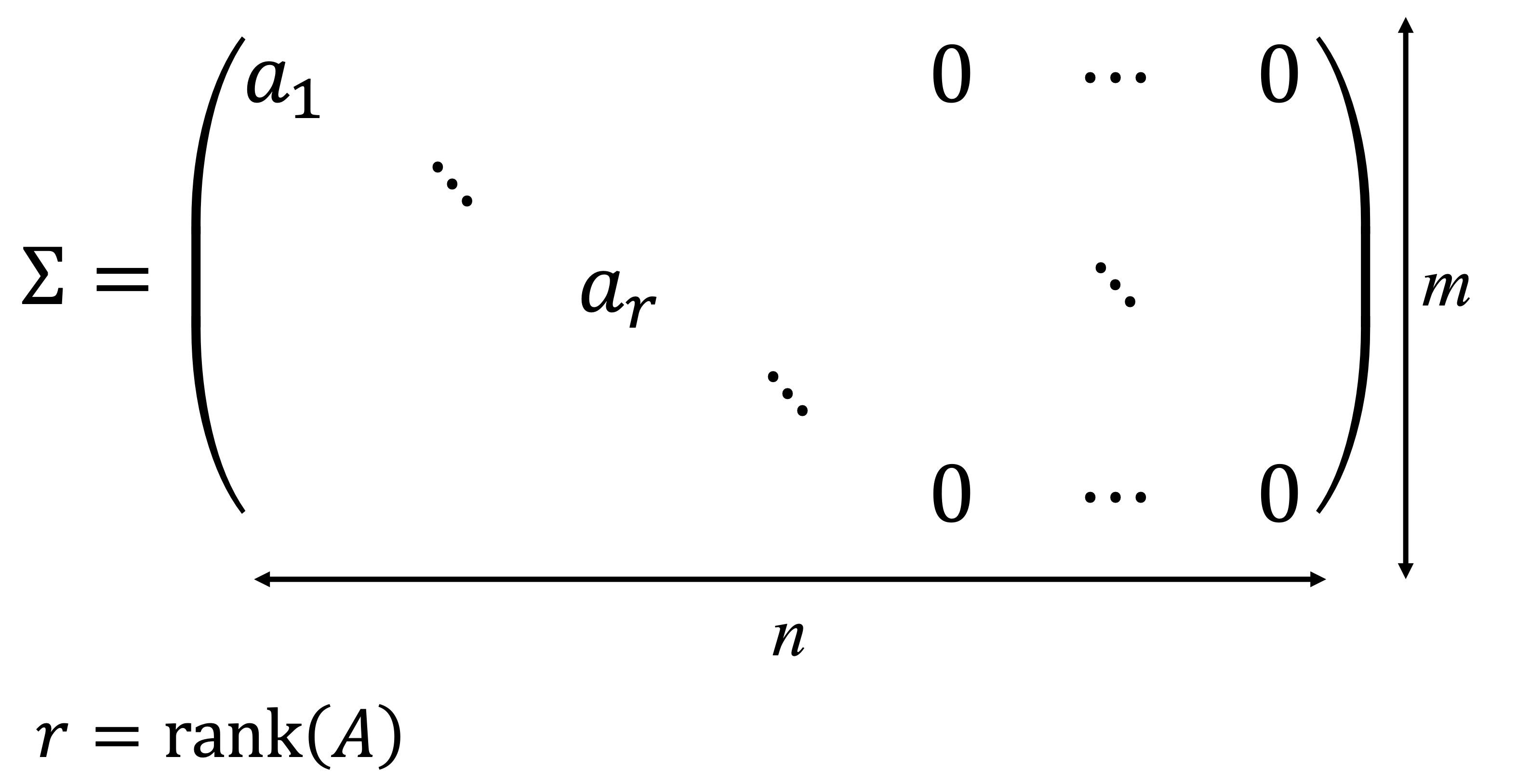
② 전체 과정

③ singular value는 AAT 혹은 ATA의 고유치의 양의 제곱근으로 정의됨
○ AAT와 ATA는 zero eigenvalue의 개수가 차이나지만, non-zero eigenvalue는 동일하게 도출됨
○ non-zero singular value의 개수 : rank(A)
○ zero singular value의 개수 : max(dim(A)[0], dim(A)[1]) - rank(A)
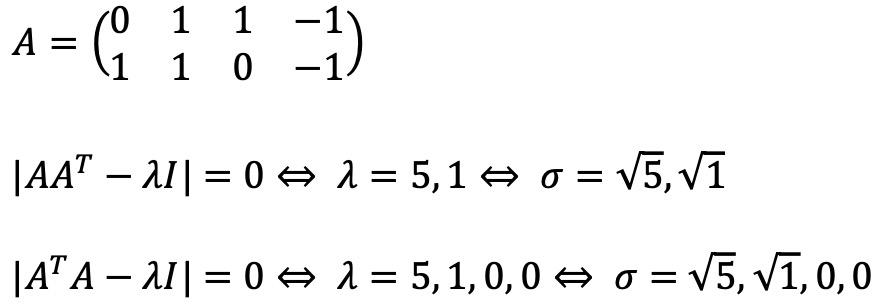
④ 파이썬 코드
# np.linalg.svd computes the SVD of a matrix
A = np.array([[4,11,14],
[8,7,-2]])
U, s, Vt=np.linalg.svd(A)
print(U)
print(s) # s is the vector of nonzero singular values
print(Vt)
⑶ 응용 1. ATA = V(∑T∑)VT : A의 singular value는 ATA의 고유치의 제곱근. 단, rank에 맞게 일부 고유치는 0으로 바뀜
⑷ 응용 2. reduced SVD : UTU = I, VTV = I를 만족하지만, U와 V가 정사각행렬이 아니므로 orthogonal matrix는 아님
A = np.array([[4,11,14],
[8,7,-2]])
U, s, Vt=np.linalg.svd(A, full_matrices=False)
print(U)
print(s)
print(Vt)
⑸ 응용 3. rank-k approximation
① k < rank (A)에 대하여, m × n 행렬 A를 m × k + k × n 행렬로 쪼개어 압축 효과를 만들 수 있음
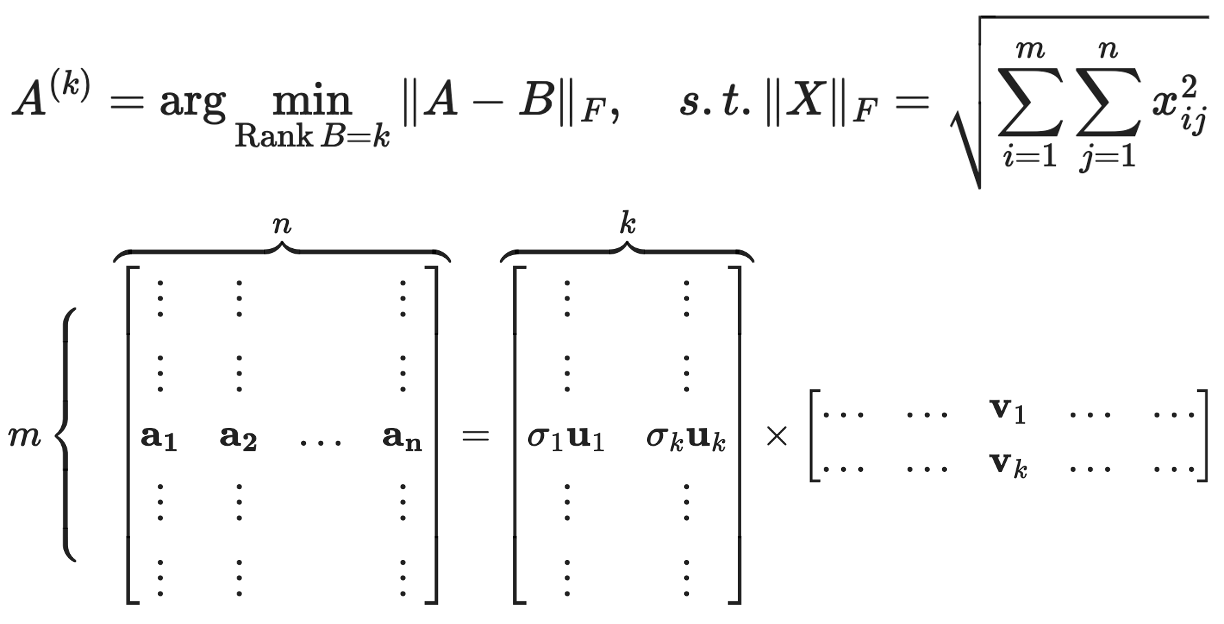
② k가 주어져 있을 때 A의 최적의 rank-k approximation을 찾는 법
○ A = U∑VT = σ1u1v1T + ··· + σrurvrT, σ1 ≥ ⋯ ≥ σr 중에서 singular value가 작은 σr, σr-1, ⋯를 제거
○ 그렇게 하면, A(k)와 A의 Frobenius distance는 다음과 같이 정의됨
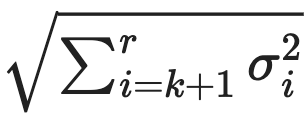
⑹ 응용 4. PCA(principal component analysis)
① 단계 1. 데이터를 중심으로 이동하여 centered data Xc를 획득
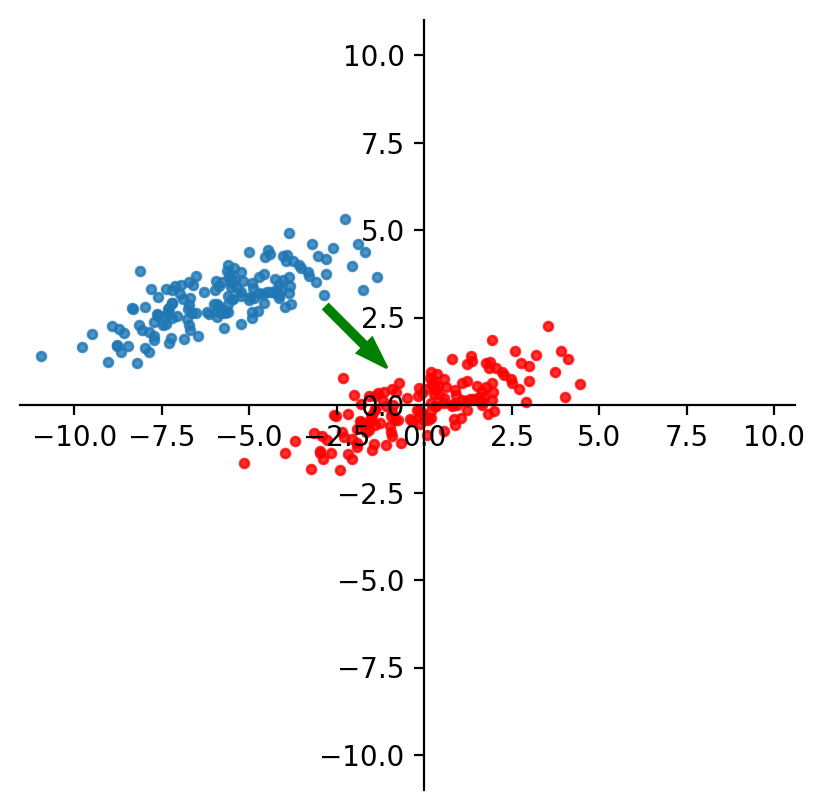
Figure. 4. PCA에서 데이터의 중심화
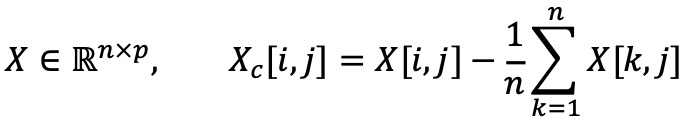
② 단계 2. C = (1/n) XcTXc를 정의
③ 단계 3. C는 symmetric이므로 직교대각화가 가능함 : C = VDVT와 같이 표현됨 (단, 이때 V는 Xc = U∑VT에서의 V와 동일함)
④ 단계 4. V의 1, 2, ···번째 열벡터는 1, 2, ···번째로 큰 고유치와 대응하는 고유벡터이자 주성분
⑤ 단계 5. 만약 첫 두 개의 PC 위에 데이터를 정사영하는 경우 다음과 같은 수식을 따름
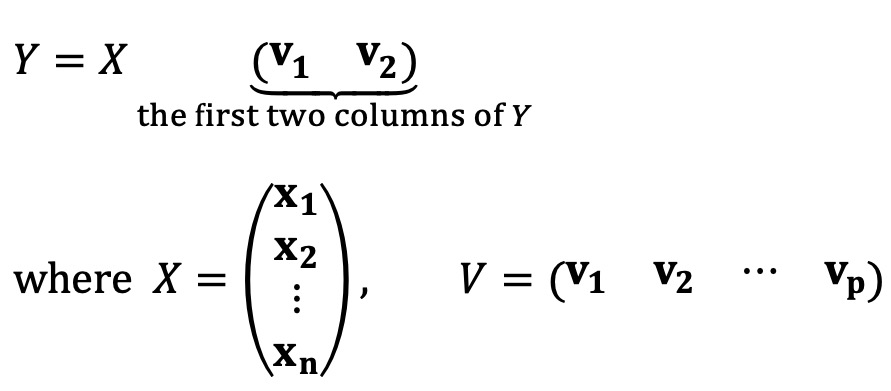
6. 종류 5. 독립성분분석(ICA, independent component analysis) [목차]
⑴ 주성분 분석과 달리, 다변량의 신호를 통계적으로 독립적인 하부 성분으로 분리하여 차원을 축소하는 기법
⑵ 예를 들어, N개의 마이크로 M개의 대화를 구분하는 상황
⑶ 독립성분의 분포는 비정규분포를 따르게 됨
⑷ matrix factorization을 이용함
7. 종류 6. PPCA(probabilistic PCA) [목차]
⑴ 수식화
① 단계 1. 관측 데이터 x가 잠재변수 z에 의해 생성된다고 가정 : 아래와 같은 변환 자체가 차원 축소 기법이 됨
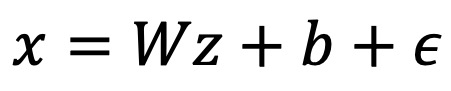
○ W : D × d 차원의 변환 행렬 (잠재 공간에서 관측 공간으로의 변환)
○ b : D 차원의 평균 벡터
○ ϵ : 노이즈. 정규분포 N(0, σ2I)를 따름
② 단계 2. 잠재 변수 z의 가정
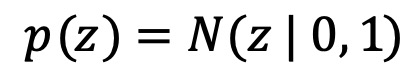
③ 단계 3. z가 주어졌을 때 x의 조건부 분포
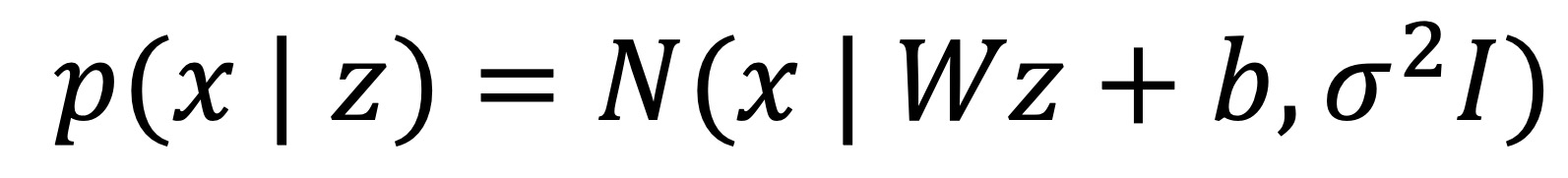
④ 단계 4. 주변 분포 p(x)
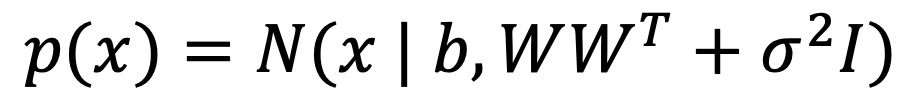
⑤ 단계 5. MLE 추정
○ 주어진 데이터로부터 b, W, σ를 추정하기 위해 최대가능도추정(MLE)을 사용
○ MLE 해는 closed-form solution으로 구해짐
○ σ → 0으로 수렴하면 정규 PCA 방식과 같아짐
⑵ 코드
import numpy as np
from numpy import shape, isnan, nanmean, average, zeros, log, cov
from numpy import matmul as mm
from numpy.matlib import repmat
from numpy.random import normal
from numpy.linalg import inv, det, eig
from numpy import identity as eye
from numpy import trace as tr
from scipy.linalg import orth
def ppca(Y,d,dia):
"""
Implements probabilistic PCA for data with missing values,
using a factorizing distribution over hidden states and hidden observations.
Args:
Y: (N by D ) input numpy ndarray of data vectors
d: ( int ) dimension of latent space
dia: (boolean) if True: print objective each step
Returns:
ss: ( float ) isotropic variance outside subspace
C: (D by d ) C*C' + I*ss is covariance model, C has scaled principal directions as cols
M: (D by 1 ) data mean
X: (N by d ) expected states
Ye: (N by D ) expected complete observations (differs from Y if data is missing)
Based on MATLAB code from J.J. VerBeek, 2006. http://lear.inrialpes.fr/~verbeek
"""
N, D = shape(Y) #N observations in D dimensions (i.e. D is number of features, N is samples)
threshold = 1E-4 #minimal relative change in objective function to continue
hidden = isnan(Y)
missing = hidden.sum()
if(missing > 0):
M = nanmean(Y, axis=0)
else:
M = average(Y, axis=0)
Ye = Y - repmat(M,N,1)
if(missing > 0):
Ye[hidden] = 0
#initialize
C = normal(loc=0.0, scale=1.0, size=(D,d))
CtC = mm(C.T, C)
X = mm(mm(Ye, C), inv(CtC))
recon = mm(X, C.T)
recon[hidden] = 0
ss = np.sum((recon-Ye)**2) / (N*D - missing)
count = 1
old = np.inf
#EM Iterations
while(count):
Sx = inv(eye(d) + CtC/ss) #E-step, covariances
ss_old = ss
if(missing > 0):
proj = mm(X,C.T)
Ye[hidden] = proj[hidden]
X = mm(mm(Ye, C), Sx/ss) #E-step: expected values
SumXtX = mm(X.T, X) #M-step
C = mm(mm(mm(Ye.T, X),(SumXtX + N*Sx).T), inv(mm((SumXtX + N*Sx), (SumXtX + N*Sx).T)))
CtC = mm(C.T, C)
ss = (np.sum((mm(X, C.T) - Ye)**2) + N*np.sum(CtC*Sx) + missing*ss_old) / (N*D)
#transform Sx determinant into numpy float128 in order to deal with high dimensionality
Sx_det = np.min(Sx).astype(np.float64)**shape(Sx)[0] * det(Sx / np.min(Sx))
objective = N*D + N*(D*log(ss)+tr(Sx)-log(Sx_det)) + tr(SumXtX) - missing*log(ss_old)
rel_ch = np.abs( 1 - objective / old )
old = objective
count = count + 1
if( rel_ch < threshold and count > 5 ):
count = 0
if(dia == True):
print('Objective: %.2f, Relative Change %.5f' %(objective, rel_ch))
C = orth(C)
covM = cov(mm(Ye, C).T)
vals, vecs = eig( covM )
ordr = np.argsort(vals)[::-1]
vals = vals[ordr]
vecs = vecs[:,ordr]
C = mm(C, vecs)
X = mm(Ye, C)
#add data mean to expected complete data
Ye = Ye + repmat(M,N,1)
return C, ss, M, X, Ye
8. 종류 7. CCA(canonical-correlation analysis) [목차]
⑴ CCA
① 문제 : 주어진 데이터 행렬 X ∈ ℝn×p, Y ∈ ℝn×q가 있을 때, 변환된 변수들의 상관계수를 최대화하는 것
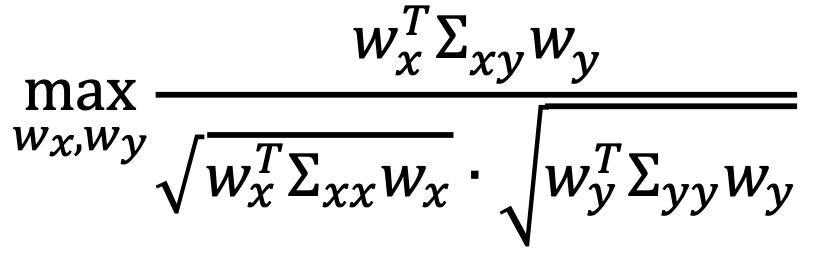
○ ∑xx = XTX : X의 공분산 행렬 ∈ ℝp×p
○ ∑yy = YTY : Y의 공분산 행렬 ∈ ℝq×q
○ ∑xy = XTY : X와 Y의 공분산 행렬 ∈ ℝp×q
○ ∑yx = ∑xyT
② 풀이 : wxT∑xxwx = 1 및 wyT∑yywy = 1 제약 조건 하에서 분자를 최적화하는 문제로 바꾼 뒤 라그랑주 승수법 적용
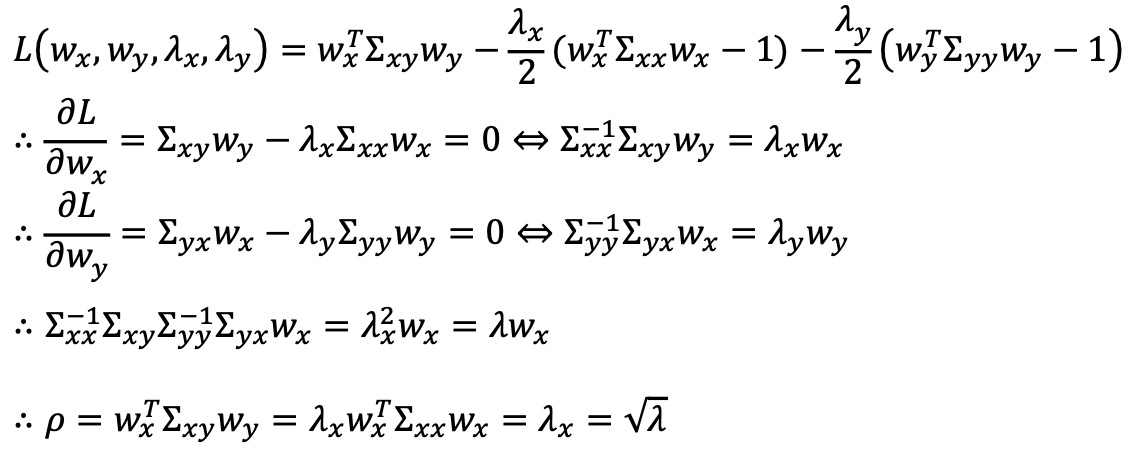
③ 결론 : ∑xx-1∑xy∑yy-1∑yx 행렬의 일반화된 고유값의 양의 제곱근이 canonical correlation이 됨
⑵ DCCA(diagonal CCA)
① 문제 : 주어진 데이터 행렬 X ∈ ℝn×p, Y ∈ ℝn×q가 있을 때
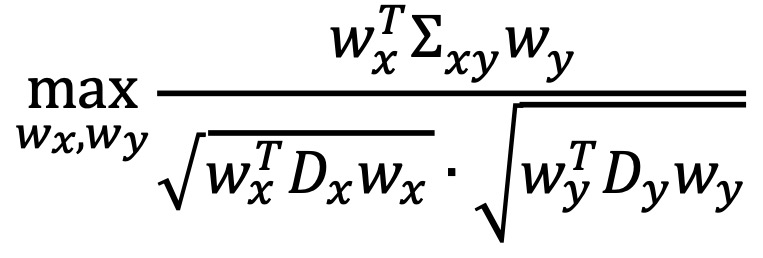
○ Dx = diag(∑xx) : 공분산 행렬의 대각 성분만 사용
○ Dy = diag(∑yy) : 공분산 행렬의 대각 성분만 사용
② 과정 : SVD 특이값이 canonical correlation 값이 됨

⑶ CCA와 DCCA의 비교
| CCA | DCCA | |
| 공분산 행렬 | 전체 사용 (∑xx, ∑yy) | 대각 성분만 사용 (Dx, Dy) |
| 풀이 | 일반화된 고유값 | SVD |
| 계산량 | 역행렬 계산 필요 (고비용) | 대각 행렬 기반 연산 (저비용) |
| 결과 해석 | 고유벡터, 고유값 | 특이벡터, 특이값 |
Table. 1. CCA와 DCCA의 비교
9. 기타 [목차]
⑴ 요인 분석(factor analysis)
① 정의 : 여러 개의 변수들로 이루어진 데이터에서 변수들 간의 상관관계를 고려하여 서로 유사한 변수들을 묶어 새로운 잠재요인을 추출하고 데이터 안의 구조를 해석하는 방법
② 데이터 안에 관찰할 수 없는 잠재적인 변수가 존재한다고 가정
③ 사회과학이나 설문조사에서 많이 활용
⑵ 다차원 척도법(MDS, multi-dimensional scaling)
① 개요
○ 정의 : 데이터 속에 잠재해 있는 패턴, 구조를 찾아내어 소수 차원의 공간에 기하학적으로 표현하는 객체 간 근접성 및 개체들 간 집단화를 시각화하는 통계 기법
○ 개체들 사이의 유사성, 비유사성을 측정하여 2차원 또는 3차원 공간 상에 점으로 표현
② 수식화 : 고차원에서의 거리 dh, 저차원에서의 거리 dl에 대하여 다음을 최소화하는 변환을 탐색
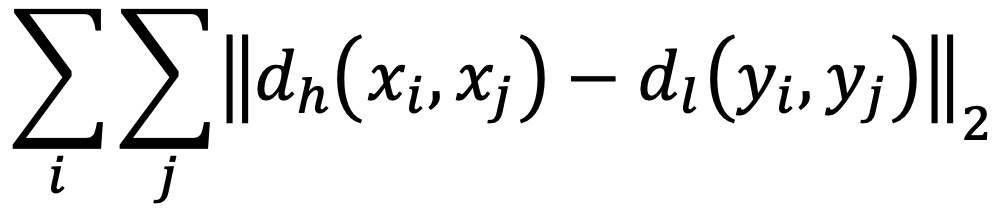
③ 특징 : gradient descent method를 사용하여 위 변환을 탐색
④ 단점 : global metric이므로 outlier에 취약함
⑶ 선형 판별 분석(LDA, linear discriminant analysis)
① 정의 : PCA와 유사하게 데이터를 저차원 공간에 투영해 차원을 축소하는 방법
⑷ RPCA(reciprocal principal component analysis)
⑸ 오토인코더(autoencoder)
⑹ PHATE
⑺ ODA
⑻ LLE
⑼ LSA
⑽ PLSA(probabilistic latent semantic analysis)
① latent class model로부터 혼합된 성분을 decomposition 할 때 사용
② 응용 : 질량 분석 데이터에서 차원축소 성분을 뺄 때 사용
입력: 2021.12.03 16:22
수정: 2024.11.16 08:43
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 6강. 분류 알고리즘 (0) | 2021.12.11 |
|---|---|
| 【알고리즘】 23강. 베이지안 최적화와 MAB (0) | 2021.12.10 |
| 【알고리즘】 16강. CNN 신경망 (0) | 2021.11.21 |
| 【알고리즘】 15강. 다층 퍼셉트론 (0) | 2021.11.21 |
| 【알고리즘】 10강. 딥러닝 개요 (0) | 2021.11.21 |





최근댓글