7-1강. SNE, symmetric-SNE, tSNE
추천글 : 【알고리즘】 7강. 차원 축소 알고리즘
1. 개요 [본문]
2. 종류 1. SNE(stochastic neighbor embedding) [본문]
3. 종류 2. symmetric-SNE [본문]
4. 종류 3. t-SNE(t-distributed SNE) [본문]
1. 개요 [목차]
⑴ 용어
① 다양체(manifold) : 고차원 공간 중에 실질적으로는 보다 저차원으로 표시 가능한 도형
② 데이터 포인트(data point) : 고차원 데이터 포인트라고도 함

③ 맵 포인트(map point) : 저차원 데이터 포인트라고도 함

⑵ 특징
① 확률 개념을 도입하여 MDS(multidimensional scaling)의 문제점을 해결
② 특징 1. 데이터에서 지역 인접성(local neighborhoods)을 보존하려고 시도하는 차원 축소 알고리즘 : 엄청 먼 데이터 포인트는 고려하지 않는 local metric
③ 특징 2. 비선형적이며 비결정적
2. 종류 1. SNE(stochastic neighbor embedding) [목차]
⑴ 정의 : 고차원 공간에서 유클리드 거리를 데이터 포인트의 유사성을 표현하는 조건부 확률로 변환하는 방법
① 유클리드 거리(Euclidean distance) : 피타고리스 정리를 이용한 거리
② 맵핑(mapping) : 고차원 데이터 포인트에서 저차원 데이터 포인트로 대응되는 사상

⑵ 고차원 데이터의 유사성을 표현하는 조건부 확률
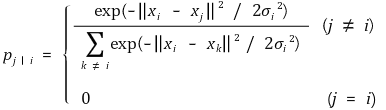
① xi : 고차원 데이터 점
② xj : 고차원 데이터 점
③ σi : xi를 중심으로 한 가우스 분포의 표준편차
⑶ 저차원 데이터의 유사성을 표현하는 조건부 확률
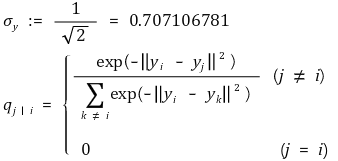
① σy = 0.707106781가 되도록 클러스터링을 하겠다는 의미
⑷ 주요 가정 : 맵핑이 잘 돼 있으면 다음과 같음
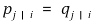
① KL 거리(Kullback-Leibler divergence)
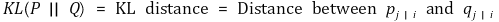
② cost function : 모든 데이터 포인트에 대한 KL 거리의 합
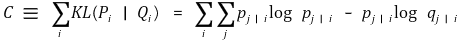
③ 전략 : cost function을 최소화하는 방향으로 Q를 업데이트
⑸ perplexity
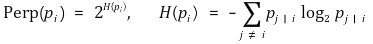
① Perp(pi) : 데이터 점 xi의 유효한 근방의 개수의 척도
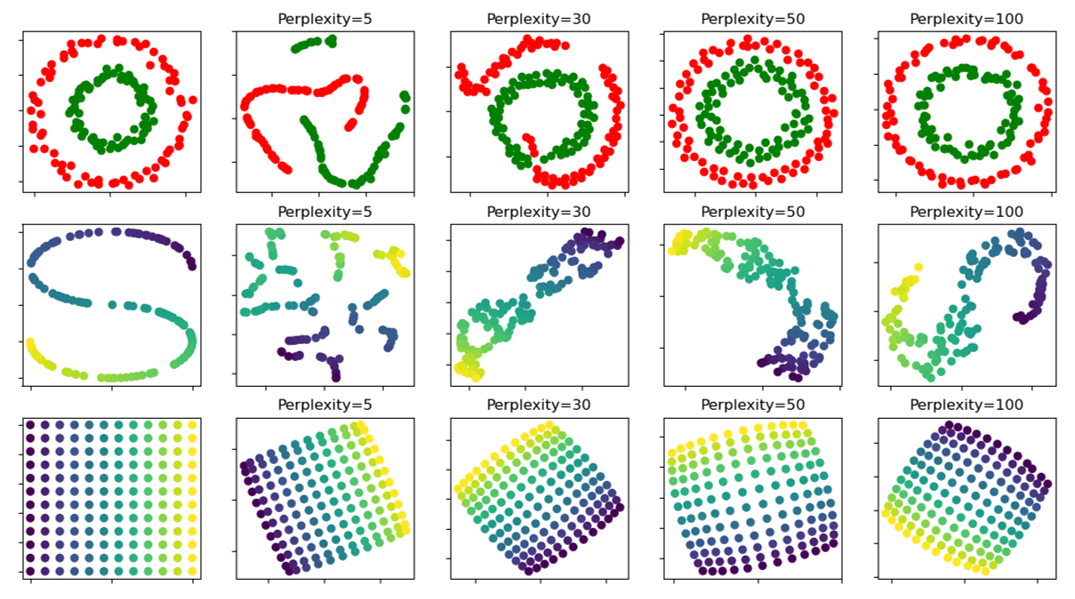
(단, 위의 예시는 t-SNE임을 유의)
② 일반적으로 perplexity는 5-50 사이로 설정
③ 실험적으로 1 ≤ perplexity ≤ 99의 범위를 갖는 것으로 관찰
④ 일정한 perplexity를 갖도록 σi를 i에 따라 다르게 설정
○ σ가 증가할수록 perplexity는 작아짐 (감소함수)
○ bisection method를 이용하여 σi를 정의
○ 1st. LEFT 값과 RIGHT 값을 설정
○ 2nd. MID ← (LEFT + RIGHT) / 2
○ 3rd. σi ← MID
○ 4th. Perp(σi) < Perp인 경우 LEFT ← MID; 2nd로 이동
○ 5th. Perp(σi) > Perp인 경우 RIGHT ← MID; 2nd로 이동
○ 6th. N번 반복 후 MID 값을 σi로 정의
⑹ cost function의 변화율
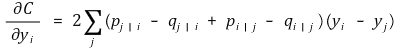
① p j | i - q j | i + p i | j - q i | j : 데이터 점의 유사도와 맵 점의 유사도의 불일치
② yi - yj : 맵상에서의 거리
⑺ 갱신 알고리즘(updating algorithm)

① 학습률(learning rate) η : 일반적으로 100 전후
② 모멘텀(momentum) α : local minimum에 빠지지 않도록 모멘텀을 도입. 초반에 0.5 전후, 후반에 0.8 전후
③ 반복수(iteration number) t : 일반적으로 1000 전후
④ (주석) 논문에서는 η 앞에 (+)가 붙는데 η > 0에서 (-)가 붙는 게 맞다고 봄
3. 종류 2. symmetric-SNE [목차]
⑴ 개요
① SNE의 문제점 : 최적화가 어려움, crowding 문제 발생
② t-SNE : 두 점의 유사도를 계산할 때, 정규분포가 아닌 student T 분포를 이용
③ symmetric-SNE : t-SNE의 개량 버전
⑵ 고차원 데이터의 유사성을 표현하는 결합확률
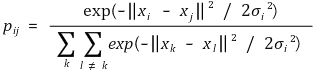
⑶ 저차원 데이터의 유사성을 표현하는 결합확률
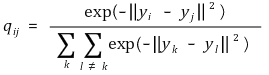
⑷ cost function
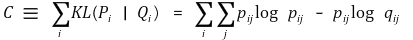
① (참고) SNE의 전략 : 조건부 확률분포 p j | i 와 q j | i 의 KL 거리를 최소화
② symmetric-SNE의 전략 : 동시 확률분포 p ji 와 q ji 의 KL 거리를 최소화
⑸ cost function의 변화율
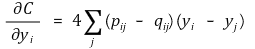
4. 종류 3. t-SNE(티스니, t-distributed SNE) [목차]
⑴ 고차원 데이터의 유사성을 표현하는 결합확률 : 가우스 분포 유사도로 변환
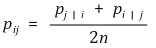
⑵ 저차원 데이터의 유사성을 표현하는 결합확률 : 자유도 1의 t 분포 유사도로 변환
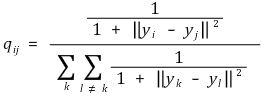
⑶ cost function
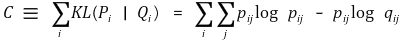
⑷ cost function의 변화율
① 정의
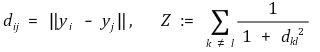
② 전개

⑸ 갱신 알고리즘(updating algorithm)
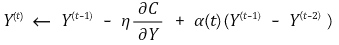
① 학습률(learning rate) η : 일반적으로 100 전후
② 모멘텀(momentum) α : local minimum에 빠지지 않도록 모멘텀을 도입. 초반에 0.5 전후, 후반에 0.8 전후
③ 반복수(iteration number) t : 일반적으로 1000 전후
④ 주석 : 논문에서는 η 앞에 (+)가 붙는데 η > 0에서 (-)가 붙는 게 맞다고 봄
⑹ R 프로그래밍
install.packages("Rtsne")
library(Rtsne)
# data consists of only numbers; no rownames, no colnames
data <- read.csv("C:/Users/data.csv")
tsne <- Rtsne(data, dims = 2, perplexity = 30, verbose = TRUE, max_iter = 500)
# Performing PCA
# Read the 14893 x 50 data matrix successfully!
# OpenMP is working. 1 threads.
# Using no_dims = 2, perplexity = 30.000000, and theta = 0.500000
# Computing input similarities...
# Building tree...
# - point 10000 of 14893
# Done in 5.06 seconds (sparsity = 0.007533)!
# Learning embedding...
# Iteration 50: error is 103.272821 (50 iterations in 4.11 seconds)
# Iteration 100: error is 88.450651 (50 iterations in 4.85 seconds)
# Iteration 150: error is 79.372908 (50 iterations in 3.18 seconds)
# Iteration 200: error is 76.927413 (50 iterations in 3.10 seconds)
# Iteration 250: error is 75.783877 (50 iterations in 3.02 seconds)
# Iteration 300: error is 2.946416 (50 iterations in 2.96 seconds)
# Iteration 350: error is 2.515109 (50 iterations in 2.84 seconds)
# Iteration 400: error is 2.244128 (50 iterations in 2.88 seconds)
# Iteration 450: error is 2.053382 (50 iterations in 2.86 seconds)
# Iteration 500: error is 1.912981 (50 iterations in 2.90 seconds)
# Fitting performed in 32.67 seconds.
exeTimeTsne<- system.time(Rtsne(data, dims = 2, perplexity=30, verbose=TRUE, max_iter = 500))
plot(tsne$Y, t = 'n', xlab = "Y1", ylab = "Y2", main = "tsne")
text(tsne$Y, labels = "○", col = "light blue")
write.csv(tsne$Y, "C:/Users/map.csv")
① Rtsne는 크기가 2.2 Gb 이상인 벡터를 할당할 수 없음 (예 : 10000 × 10000 행렬)
② 1000 × 10000의 행렬을 처리하는데 1분 30초 소요됨
③ ERROR 메시지 : "Remove duplicates before running TSNE"
○ 해결방법 : Rtsne(data, dims = 2, perplexity = 30, verbose = TRUE, max_iter = 500, check_duplicates = FALSE)
⑺ 레퍼런스
① L.J.P. van der Maaten and G.E. Hinton. Visualizing High-Dimensional Data Using t-SNE. Journal of Machine Learning Research 9(Nov):2579-2605, 2008. (ref)
② L.J.P. van der Maatem. Barnes-Hut-SNE. In Proceedings of the International Conference on Learning Representations, 2013.
③ https://github.com/jkrijthe/Rtsne
입력: 2019.10.05 17:32
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 25-1강. 뉴턴-랩슨법(Newton-Raphson method, Newton method) (0) | 2019.11.12 |
|---|---|
| 【알고리즘】 6-1강. Calibrated Classification Model (0) | 2019.11.08 |
| 【알고리즘】 12강. 진화학습 (0) | 2018.06.09 |
| 【알고리즘】 25강. 수치해석 알고리즘 (0) | 2016.12.11 |
| 【컴퓨터과학】 Dll Explicit Linking (0) | 2016.08.04 |



최근댓글