25강. 수치해석 알고리즘 모음
추천글 : 【알고리즘】 알고리즘 목차
1. Thomas 알고리즘 [본문]
2. Gauss 소거법 알고리즘 [본문]
3. Doolittle 법 [본문]
4. Cholesky 법 [본문]
5. Jacobi 반복법 [본문]
6. Gauss-Seidel 알고리즘 [본문]
7. 개선된 Euler 알고리즘 (Heum의 방법) [본문]
8. 고전적인 RUNGE-KUTTA 알고리즘 [본문]
9. 개선된 RUNGE-KUTTA 알고리즘 [본문]
10. RUNGE-KUTTA-FEHLBERG 알고리즘 [본문]
11. Adams-Bashforth 알고리즘 [본문]
12. Adams-Moulton 알고리즘 [본문]
13. Explicit Method [본문]
14. Fully (Simple) Implicit Method [본문]
15. Crank-Nicolson Method [본문]
16. 적분의 근사식 [본문]
17. 최적화 알고리즘 [본문]
1. Thomas 알고리즘 (A → A* = [ajk] = [Ar]) [목차]
이 알고리즘은 Tridiagonal Matrix인 A가 유일해, x = [xj]를 계산하거나 유일해가 존재하지 않음을 나타낸다.
(단, A의 대각성분을 f, 대각아래 성분을 e, 대각위 성분을 g라고 하자.)
INPUT: aj, n+1 = bj인 n × (n+1) 첨가행렬 A* = [ajk]
OUTPUT: 식 (1)의 해 x = [xj] 또는 식이 유일해를 갖지 않음을 알리는 메시지
// DECOMPOSITION
DO k = 2, ..., n
ek = ek / fk-1
fk = fk - ek × gk-1
END DO
// FORWARD SUBSTITUTION
DO k = 2, ..., n
rk = rk - ek × rk-1
END DO
// BACKWARD SUBSTITUTION
xn = rn / fn
DO k = n - 1, ..., 1
xk = (rk - gk × xk+1) / fk
END DO
End GAUSS
2. Gauss 소거법 알고리즘 (A → A* = [ajk] = [Ab]) [목차]
이 알고리즘은 유일해, x = [xj]를 계산하거나 유일해가 존재하지 않음을 나타낸다.
INPUT: aj, n+1 = bj인 n × (n+1) 첨가행렬 A* = [ajk]
OUTPUT: 식 (1)의 해 x = [xj] 또는 식이 유일해를 갖지 않음을 알리는 메시지
For k = 1, ..., n - 1 do:
m = k
For j = k + 1, ..., n, do:
If |amk| < |ajk| then m = j End
End
If amk = 0 then
OUTPUT "유일해 없음"
Stop
End
Else k행을 m행과 교환
For j = k + 1, ..., n, do:
mjk = ajk / akk
For p = k + 1, ..., n + 1, do:
ajp = ajp - mjkakp
End
End
End
If ann = 0 then
OUTPUT "유일해가 존재하지 않음"
Stop
End
xn = an,n+1 / ann [역대입 시작]
For i = n - 1, ..., 1, do:
xi = (1/aii)(ai,n+1 - (ai,i+1xi+1 + ... + ai, nxn))
End
OUTPUT x = [xj]
Stop
End GAUSS
3. Doolittle법 [목차]
Ax = LUx = b
Ux = L-1b = y
x = U-1y
4. Cholesky법 [목차]
Ax = LLTx = b
LTx = L-1b = y
x = (LT)-1y
5. Jacobi 반복법 [목차]
ex.
x1 - 0.25x2 - 0.25x3 = 50 x1 = 0.25x2 + 0.25x3 + 50
-0.25x1 + x2 - 0.25x4 = 50 x2 = 0.25x1 + 0.25x4 + 50
-0.25x1 + x3 - 0.25x4 = 25 x3 = 0.25x1 + 0.25x4 + 25
-0.25x2 - 0.25x3 + x4 = 25 x4 = 0.25x2 + 0.25x3 + 25
cf.
x(m+1) = b - Lx(m) - Ux(m) = b - (L+U)x(m)
6. Gauss-Seidel 알고리즘 (A, b, x(0), ε, N) [목차]
이 알고리즘은 A = [ajk]가 ajj ≠ 0, j = 1, ..., n인 n × n 행렬일 때 주어진 초기 근사해 x(0)에 대해 Ax = b의 해 x를 계산한다.
INPUT: A, b, 초기 근사값 x(0), 허용 오차 ε, 최대 반복수 N
OUTPUT: 근사해 x(m) = [xj(m)] 또는 x(N)이 허용오차 조건을 만족하지 않는다는 오류 메시지
For m = 0, ..., N - 1 do:
For j = 1, ..., n do:
xj(m) = (1/ajj)(bj - (aj1x1(m+1) + ... + aj, j-1xj-1(m+1)) - (aj, j+1xj+1(m) + ... + ajnxn(m)))
End
If ∀j, |xj(m+1) - xj(m)| then
OUTPUT x(m+1)
Stop
End
End
OUTPUT
End GAUSS-SEIDEL
ex.
x1 - 0.25x2 - 0.25x3 = 50 x1 = 0.25x2 + 0.25x3 + 50
-0.25x1 + x2 - 0.25x4 = 50 x2 = 0.25x1 + 0.25x4 + 50
-0.25x1 + x3 - 0.25x4 = 25 x3 = 0.25x1 + 0.25x4 + 25
-0.25x2 - 0.25x3 + x4 = 25 x4 = 0.25x2 + 0.25x3 + 25
cf.
x(m+1) = b - Lx(m+1) - Ux(m) ⇔ x(m+1) = (I + L)-1b - (I + L)-1Ux(m)
7. 개선된 Euler 알고리즘 (Heum의 방법) (f, x0, y0, h, N) [목차]
이 알고리즘은 초기값 문제 y' = f(x, y), y(x0) = y0의 해를 등간격 x1 = x0 + h, x2 = x0 + 2h, ..., xN = x0 + Nh에서 계산한다.
단, f는 [x0, xN] 구간에서 이 문제가 유일한 해를 갖는 함수이다.
INPUT: 초기값 x0, y0, 단계간격 h, 단계수 N
OUTPUT: xn+1 = x0 + (n+1)h에서 해 y(xn+1)에 관한 근사화 yn+1 (n=0, ..., N-1)
For n = 0, 1, ..., N-1 do:
xn+1 = xn + h
k1 = hf(xn+yn)
k2 = hf(xn+1, yn+k1)
yn+1 = yn + 0.5(k1 + k2)
OUTPUT xn+1, yn+1
End
Stop
End EULER
8. 고전적인 RUNGE-KUTTA 알고리즘 (f, x0, y0, h, N) [목차]
이 알고리즘은 초기값 문제 y' = f(x, y), y(x0) = y0의 해를 등간격점
x1 = x0 + h, x2 = x0 + 2h, ..., xN = x0 + Nh
에서 계산한다. 여기서 f는 주어진 문제가 구간 [x0, xN]에서는 유일한 해를 갖도록 정해진다.
INPUT: 초기값 x0, y0, 단계간격 h, 단계수 N
OUTPUT: 단계점 xn+1 = x0 + (n+1)h에서 해 y(xn+1)의 근사값 yn+1 (n = 0, ..., N-1)
For n = 0, 1, ..., N-1 do:
k1 = hf(xn, yn)
k2 = hf(xn + 0.5h, yn + 0.5k1)
k3 = hf(xn + 0.5h, yn + 0.5k2)
k4 = hf(xn + h, yn + k3)
xn+1 = xn + h
yn+1 = yn + (1/6)(k1 + 2k2 + 2k3 + k4)
OUTPUT xn+1, yn+1
End
Stop
End RUNGE-KUTTA
9. 개선된 RUNGE-KUTTA 알고리즘 (f, x0, y0, h, N) [목차]
이 알고리즘은 초기값 문제 y' = f(x, y), y(x0) = y0의 해를 등간격점
x1 = x0 + h, x2 = x0 + 2h, ..., xN = x0 + Nh
에서 계산한다. 여기서 f는 주어진 문제가 구간 [x0, xN]에서는 유일한 해를 갖도록 정해진다.
INPUT: 초기값 x0, y0, 단계간격 h, 단계수 N
OUTPUT: 단계점 xn+1 = x0 + (n+1)h에서 해 y(xn+1)의 근사값 yn+1 (n = 0, ..., N-1)
For n = 0, 1, ..., N-1 do:
k1 = hf(xn, yn)
k2 = hf(xn + (1/4)h, yn + (1/4)k1)
k3 = hf(xn + (3/8)h, yn + (3/32)k1 + (9/32)k2)
k4 = hf(xn + (12/13)h, yn + (1932/2197)k1 - (7200/2197)k2 + (7296/2197)k3)
k5 = hf(xn + h, yn + (439/216)k1 - 8k2 + (3680/513)k3 - (845/4104)k4)
xn+1 = xn + h
yn+1 = yn + (25/216)k1 + (1408/2565)k3 + (2197/4104)k4 + (-1/5)k5
OUTPUT xn+1, yn+1
End
Stop
End RUNGE-KUTTA
10. RUNGE-KUTTA-FEHLBERG 알고리즘 (f, x0, y0, h, N) [목차]
이 알고리즘은 초기값 문제 y' = f(x, y), y(x0) = y0의 해를 등간격점
x1 = x0 + h, x2 = x0 + 2h, ..., xN = x0 + Nh
에서 계산한다. 여기서 f는 주어진 문제가 구간 [x0, xN]에서는 유일한 해를 갖도록 정해진다.
INPUT: 초기값 x0, y0, 단계간격 h, 단계수 N
OUTPUT: 단계점 xn+1 = x0 + (n+1)h에서 해 y(xn+1)의 근사값 yn+1 (n = 0, ..., N-1)
For n = 0, 1, ..., N-1 do:
k1 = hf(xn, yn)
k2 = hf(xn + (1/4)h, yn + (1/4)k1)
k3 = hf(xn + (3/8)h, yn + (3/32)k1 + (9/32)k2)
k4 = hf(xn + (12/13)h, yn + (1932/2197)k1 - (7200/2197)k2 + (7296/2197)k3)
k5 = hf(xn + h, yn + (439/216)k1 - 8k2 + (3680/513)k3 - (845/4104)k4)
k6 = hf(xn + (1/2)h, yn - (8/27)k1 + 2k2 + (3544/2565)k3 - (1859/4104)k4 - (11/40)k5)
xn+1 = xn + h
yn+1 = yn + (16/135)k1 + (6656/12825)k3 + (28561/56430)k4 + (-9/50)k5 + (2/55)k6
OUTPUT xn+1, yn+1
End
Stop
End RUNGE-KUTTA
11. Adams-Bashforth 알고리즘 (xn, xn-1, xn-2, xn-3, fn, fn-1, fn-2, fn-3, h, N) [목차]
이 알고리즘은 x0을 포함한 어떤 열린 구간에서 유일한 해를 가지는 초기값 문제
y' = f(x, y), y(x0) = y0, fn = (xn, yn)
를 고려한다. 이 방법은 피적분함수 f(x, y(x))를 Newton의 후진차분공식을 써서 보간다항식으로 대체하고 적분하는 것이다.
INPUT: xn, xn-1, xn-2, xn-3, fn, fn-1, fn-2, fn-3, h, N
OUTPUT: 단계점 xn+m = x0 + (n+m)h에서 해 y(xn+m)의 근사값 yn+m (m = 1, ..., N)
k4 = hfn
k3 = hfn-1
k2 = hfn-2
k1 = hfn-3
For m = 1, ..., N do:
xn+m = xn+m-1 + h
yn+m = yn+(m-1) + (1/24)(55k4 - 59k3 + 37k2 - 9k1)
k1 = k2
k2 = k3
k3 = k4
k4 = hf(xn+m, yn+m)
OUTPUT xn+m, yn+m
End
Stop
End ADAMS-BASHFORTH
12. Adams-Moulton 알고리즘 (xn, xn-1, xn-2, xn-3, fn, fn-1, fn-2, fn-3, h, N) [목차]
이 알고리즘은 x0을 포함한 어떤 열린 구간에서 유일한 해를 가지는 초기값 문제
y' = f(x, y), y(x0) = y0, fn = (xn, yn)
를 고려한다. 이 방법은 예측자-수정자 방법을 추가한 것이다. 오차추정은 다음과 같다.
εn+1 = (1/15)(yn+1 - y*n+1)
INPUT: xn, xn-1, xn-2, xn-3, fn, fn-1, fn-2, fn-3, h, N
OUTPUT: 단계점 xn+m = x0 + (n+m)h에서 해 y(xn+m)의 근사값 yn+m (m = 1, ..., N)
k4 = hfn
k3 = hfn-1
k2 = hfn-2
k1 = hfn-3
For m = 1, ..., N do:
xn+m = xn+m-1 + h
y*n+m = yn+(m-1) + (1/24)(55k4 - 59k3 + 37k2 - 9k1)
k* = f(xn+m, y*n+m)
yn+m = yn+(m-1) + (1/24)(9k* + 19k4 - 5k3 + k2)
k1 = k2
k2 = k3
k3 = k4
k4 = hf(xn+m, yn+m)
OUTPUT xn+m, yn+m
End
Stop
End ADAMS-MOULTON
13. Explicit Method [목차]
x(m+1) = Ax(m) + b
ex.
3×3: A = ((1 - 2λ, λ, 0)T, (λ, 1 - 2λ, λ)T, (0, 1 - 2λ, λ)T), b = (λx0, 0, λxn+1)T
14. Fully (Simple) Implicit Method [목차]
x(m+1) = A-1x(m) - A-1b
ex.
3×3: A = ((1 + 2λ, -λ, 0)T, (-λ, 1 + 2λ, -λ)T, (0, 1 + 2λ, -λ)T), b = (λx0, 0, λxn+1)T
15. Crank-Nicolson Method [목차]
x(m+1) = Aim-1(Aexx(m) + bex) - A-1bim
ex.
3×3: A = ((1 + 2λ, -λ, 0)T, (-λ, 1 + 2λ, -λ)T, (0, 1 + 2λ, -λ)T), b = (λx0, 0, λxn+1)T
16. 적분의 근사식 [목차]
⑴ 사다리꼴 법칙(trapezoidal law) : 적분 수치해석 기법
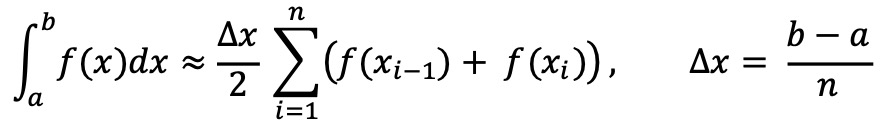
⑵ 심슨 법칙(Simpson formula) : 적분 수치해석 기법. 사다리꼴 기법에 비해 정확도가 높음
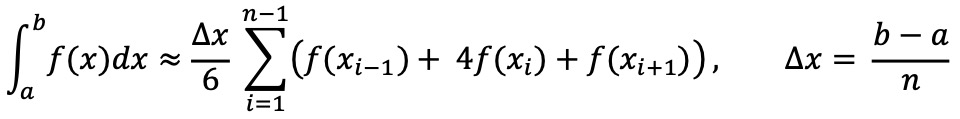
⑶ 심슨 3/8 법칙 : 적분 수치해석 기법. 심슨 법칙에 비해 정확도가 더 높음
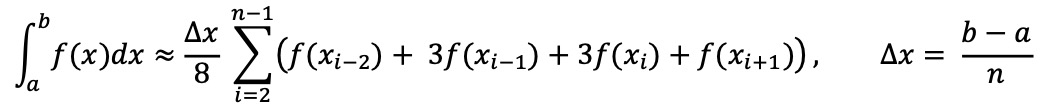
⑷ 보데(Bode) 법칙
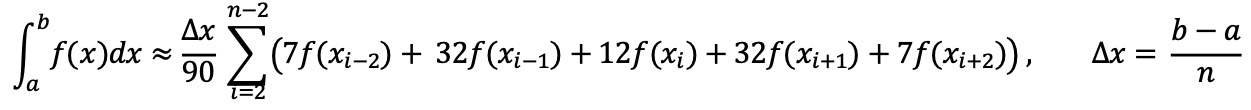
⑸ 이동평균법
17. 최적화 알고리즘 [목차]
⑴ 뉴턴-렙슨법(Newton-Raphson method)
⑶ Nelder-Mead method (아메바 방법, 넬더-미드 방법, 활강단체법) : 다차원 공간의 손실함수의 최솟값 또는 최댓값을 찾기 위한 방법
import numpy as np
from scipy.optimize import minimize
from scipy.stats import spearmanr
def model(X, coeffs):
return np.sum(X.T * coeffs, axis=1)
def objective_function(coeffs, X, target):
prediction = model(X, coeffs)
return -spearmanr(target, prediction)[0]
def optimize_spearman(X, target, initial_guess=None):
if initial_guess is None:
initial_guess = np.zeros(X.shape[0]) # Default to zero coefficients
result = minimize(objective_function, initial_guess, args=(X, target), method='Nelder-Mead')
optimal_coeffs = result.x
maximized_corr = -objective_function(optimal_coeffs, X, target)
return optimal_coeffs, maximized_corr
# Example usage
# new_bulk = np.array(...) # Replace with your 11x471 matrix
# target_vector = np.array(...) # Replace with your 471-D target vector
# optimal_coeffs, maximized_corr = optimize_spearman(new_bulk, target_vector)
# print("Optimal coefficients:", optimal_coeffs)
# print("Maximized Spearman Correlation:", maximized_corr)
⑹ BFGS method (Broyden-Fletcher-Goldfarb-Shanno optimization)
① 정의 : Newton method에서 Hessian matrix의 역행렬 계산량이 많기 때문에 이를 근사한 다른 그래디언트를 사용
② 수식화
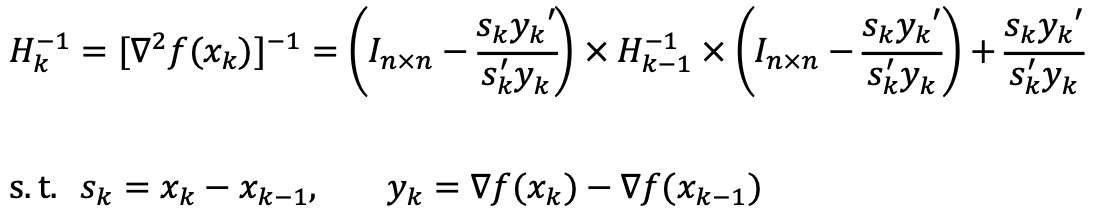
⒄ Nesterov method
⒅ SANN(simulated annealing)
① 느린 stochastic global optimization optimizer
② 미분 불가능하거나 non-convex 함수 등 난해한 함수들에 잘 작동함
⒆ 프로그래밍 관련
① 최적화 알고리즘 관련 R 패키지 및 함수 : RSolnp, optim, GenSA, alabama
입력: 2016.12.11 02:10
수정: 2024.03.28 22:20
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 7-1강. SNE, symmetric-SNE, tSNE (2) | 2019.10.05 |
|---|---|
| 【알고리즘】 12강. 진화학습 (0) | 2018.06.09 |
| 【컴퓨터과학】 Dll Explicit Linking (0) | 2016.08.04 |
| 【알고리즘】 26강. RSA 알고리즘 (0) | 2016.06.23 |
| 【알고리즘】 5강. 회귀 알고리즘 (0) | 2016.06.22 |


최근댓글