20강. 오토인코더(autoencoder)
추천글 : 【알고리즘】 알고리즘 목차
1. 개요 [본문]
2. 종류 1. 변분 오토인코더 [본문]
3. 종류 2. 그래프 오토인코더 [본문]
4. 종류 3. matrix factorization [본문]
5. 종류 4. latent topic model [본문]
6. 종류 5. 생성적 적대 신경망 [본문]
7. 종류 6. flow model [본문]
1. 개요 [목차]
⑴ 정의 : 입력 데이터를 최대한 압축시킨 후, 압축된 데이터를 다시 본래의 형태로 복원시키는 신경망
① 인코더(encoder) : 입력층에서부터 은닉층으로의 인공 신경망. 인지 네트워크라고도 함
○ 인지 네트워크(recognition network) : 패턴을 감지하고 의미를 부여하는 특수화된 네트워크
② 디코더(decoder) : 은닉층에서부터 출력층으로의 인공 신경망. 생성 네트워크라고도 함
○ 생성 네트워크(generative network) : 입력 데이터와 매우 유사한 새로운 데이터를 생성할 수 있는 네트워크
○ 오토인코더에서 디코더는 최대한 단순해야 함 : 그래서 디코어에서 GCN은 잘 쓰지 않음
③ 인코더와 디코더가 함께 트레이닝 됨
Figure. 1. 오토인코더의 구조
⑵ 수식화
Z = Eθ(X), X̂ = Dϕ(Z)
① Z : latent variable
② Eθ : 인코더 네트워크
③ X̂ : 재구성된 입력
④ Dϕ : 디코더 네트워크
⑶ 특징
① 비지도 학습 신경망
② 인코더는 차원 축소 역할을 수행
③ 디코더는 생성 모델의 역할을 수행
④ 입력층의 노드 개수는 출력층의 노드 개수와 동일
⑤ 은닉층의 노드 개수는 입력층의 노드 개수보다 작음
⑥ 차원 축소 알고리즘도 오토인코더의 한 예시라고 할 수 있음
⑷ 효과
① 효과 1. 데이터 압축 : 은닉층이 입력층보다 더 작은 개수의 노드를 가지면, 이 네트워크는 입력 데이터를 압축할 수 있음
② 효과 2. 데이터 추상화 : 복잡한 데이터를 다차원 벡터으로 변환하여 입력 데이터 분류 혹은 재조합을 가능케 함
○ 이러한 다차원 벡터를 은닉층, 피처(feature)라고도 함
○ 재조합 알고리즘으로는 대표적으로 PCA 알고리즘이 있음
③ 효과 3. 은닉 변수 추론 : 입력 데이터를 구성하는 prior를 latent variable로 두면, 오토인코더는 이를 추론하는 기능을 함
○ 디콘볼루션(deconvolution)이라고도 함
2. 종류 1. 변분 오토인코더(VAE, variational autoencoder) [목차]
⑴ 개요
① 알려진 확률분포를 도입하기 위해 잠재공간 및 변분추론을 사용함
② 확률분포의 종류에 따라 ZINB 오토인코더(zero-inflated negative binomial autoencoder) 등이 있음
⑵ 구성
① 인코더 : 입력 데이터를 은닉층에서의 확률분포, 즉 parametrized distribution으로 맵핑함
② 디코더 : parameterized distribution을 Bayesian inference에서의 prior로 보고 출력층을 맵핑함
○ 학습 : parametric posterior와 true posterior 간의 차이를 비용함수를 통해 최소화
③ 오토인코더와의 차이 : 오토인코더는 결정론적인 데 반해, 변분 오토인코더는 확률론적
④ latent 매칭을 자연스럽게 하는 것은 오토인코더보다 변분 오토인코드가 더 좋음
⑶ 수식화
Z ~ qθ(Z | X), X̂ = Dϕ(Z)
① Z : latent variable
② qθ : 조건부 확률분포
③ X̂ : 재구성된 입력
⑷ 응용 1. β-VAE : 각 임베딩 축이 나이, 성별, 인종 등과 각각 관련됨
3. 종류 2. 그래프 오토인코더(GAE, graph autoencoder) [목차]
⑴ 그래프 이론 및 라플라스 행렬을 이용하여 오토인코더와 상당히 유사한 손실함수가 정의됨
⑵ 그래프 오토인코더가 변분추론과 결합한 경우를 그래프 변분 오토인코더(VGAE, variational graph autoencoder)라고 함
4. 종류 3. matrix factorization [목차]
⑴ 정의 : 알고 있는 A 행렬을 W 행렬과 H 행렬의 곱으로 분해하는 알고리즘. A ~ W × H
① A 행렬 : 샘플-특성을 나타내는 행렬. 샘플로부터 알 수 있음
② H 행렬 : 변수-특성을 나타내는 행렬
③ K means clustering, PCA 알고리즘과 유사함
④ 오토인코더는 non-linear transformation을 포함하므로 matrix factorization보다 넓은 개념
⑤ 다음 알고리즘들은 least square method에 기반을 두고 있지만, gradient descent method 등을 활용할 수도 있음
⑵ 알고리즘 : R = UV, R ∈ ℝ5×4, U ∈ ℝ5×2, V ∈ ℝ2×4인 U, V를 탐색
import numpy as np
R = np.outer([3,1,4,2.,3],[1,1,0,1]) + np.outer([1,3,2,1,2],[1,1,4,1])
U=np.random.rand(5,2)
V=np.random.rand(2,4)
for i in range(3):
V,_,_,_=np.linalg.lstsq(U, R, rcond=None)
Ut,_,_,_=np.linalg.lstsq(V.T, R.T, rcond=None)
U=Ut.T
U@V # it is similar to R!
⑶ 3-1. NMF(non-negative matrix factorization)
import numpy as np
R = np.outer([3,1,4,2.,3],[1,1,0,1]) + np.outer([1,3,2,1,2],[1,1,4,1])
U=np.random.rand(5,2)
V=np.random.rand(2,4)
for i in range(20):
V,_,_,_=np.linalg.lstsq(U, R, rcond=None)
V = np.where(V >= 0, V, 0) #set negative entries equal zero
Ut,_,_,_=np.linalg.lstsq(V.T, R.T, rcond=None)
U=Ut.T
U = np.where(U >= 0, U, 0) #set negative entries equal zero
U@V # it is similar to R!
⑷ 3-2. matrix completion (Netflix 알고리즘) : 마스킹된 R에 대하여 matrix factorization을 진행하는 것
import numpy as np
R = np.outer([3,1,4,2.,3],[1,1,0,1]) + np.outer([1,3,2,1,2],[1,1,4,1])
mask=np.array([[1.,1,1,1],
[1,0,0,0],
[1,0,0,0],
[1,0,0,0],
[1,0,0,0]])
U=np.random.rand(5,2)
V=np.random.rand(2,4)
RR = U@V
RR = RR*(1-mask)+R*mask
for i in range(20):
V,_,_,_=np.linalg.lstsq(U, R, rcond=None)
V = np.where(V >= 0, V, 0)
Ut,_,_,_=np.linalg.lstsq(V.T, R.T, rcond=None)
U=Ut.T
U = np.where(U >= 0, U, 0)
RR = U@V
RR = RR*(1-mask)+R*mask
RR*(1-mask)+R*mask # it is similar to R!
⑸ 3-3. SVD(singular value decomposition)
⑹ 응용 1. cell type classification
① 조직으로부터 얻은 scRNA-seq로부터 cell type proportion을 얻기 위한 목적
② cell type heterogeneity에 의한 confounding effect를 줄이는 게 중요
③ 1-1. constrained linear regression
④ 1-2. reference-based approach
○ 1-2-1. CIBERSORT(cell-type identification by estimating relative subsets of RNA transcript) : 샘플별로 cell type proportion, p value를 확인할 수 있음
⑺ 응용 2. joint NMF : 멀티오믹스까지 확장하게 함
⑻ 응용 3. metagene 추출
⑼ 응용 4. Starfysh : 다음은 공간전사체에서 archetype을 추론하고, 각 archetype을 대표하는 anchor를 결정하는 알고리즘
① 단계 1. 오토인코더 구성
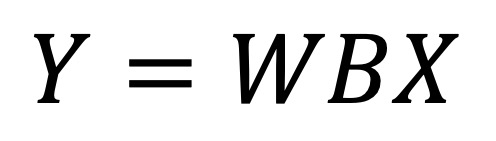
○ X ∈ ℝS×G : 입력 데이터 (스팟 × 유전자)
○ D : archetype의 수
○ B ∈ ℝD×S : 인코더. archetype을 추론하는 상황으로, 이때 각 archetype별로 전체 스팟에 대한 분포의 합은 1이어야 함
○ H = BX : latent variable
○ W ∈ ℝS×D : 디코더. 입력 데이터를 재구성하는 상황으로, 이때 각 스팟별로 전체 archetype 가중치의 합이 1이어야 함
○ Y = WBX : 재구성된 입력
② 단계 2. 최적화 알고리즘을 풀어 W, B를 계산
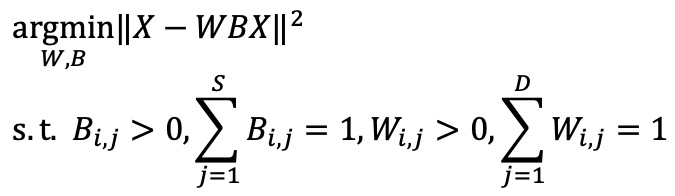
③ 단계 3. W 행렬에서 각 archetype에 대한 가중치가 가장 높은 스팟들이 anchor spot으로 선택됨
④ 단계 4. granularity 조정 : archetype 간의 거리가 가까운 경우 이를 병합하거나, 그 거리를 조정하는 계층적 구조를 사용
⑤ 단계 5. 각 anchor 별로 nearest spot을 탐색하여 archetypal community를 형성하고 마커 유전자를 탐색
⑥ 단계 6. signature gene set이 주어지는 경우, 기존의 gene set에 archetypal marker gene들을 추가하고 anchor를 다시 계산
○ 이때 stable marriage matching 알고리즘을 활용하여 각 archetype은 가장 유사한 signature와 대응됨
5. 종류 4. latent topic model [목차]
⑴ 4-1. unigram
⑵ 4-2. LSI (latent semantic indexing)
① 응용 1. probabilistic LSI
○ 단점 1. 자연어로된 문서를 위한 생성형 모델로 적합하지 않음 : 학습에 사용되지 않은 문서를 적절히 확률적 모델링하기 여러움
○ 단점 2. 파라미터의 개수가 학습에 사용된 문서의 개수에 선형 비례함
⑶ 4-3. LDA (latent Dirichlet allocation)
① 개요
○ 정의 : document × word proportion이 주어져 있고 이를 document × topic, topic × word proportion으로 구분하는 것
○ LDA 모델에서의 latent multinomial variable을 topic이라고 함
○ NMF와 비슷하게 sparse matrix를 생성시킴
② 수식화 : 문서 d의 topic 분포 θd, topic k의 단어 분포 βk에 대하여
③ 응용 1. 실제 LDA 모델
○ 전제 : 파라미터 α, β, topic mixture의 결합 분포 θ, N개의 topic의 집합 z, N개의 단어의 집합 w
○ 목표 : θ, z를 구하기 위해 베이즈 정리(Bayes theorem)를 이용
○ 결합확률분포
○ θ, z를 구하기 위해 variational EM(expectation maximization)을 사용
④ 응용 2. two-level model : hidden topic variable z에 대하여
○ 단어의 생성확률을 기존 LDA는 mixture of multinomials로 모델링하는 반면 ProdLDA는 product of experts로 모델링함
○ 장점 1. LDA는 θd ~ Dirichlet(α)와 같이 확률분포의 샘플링을 직접 모델링하여 변분추론, Gibbs 샘플링과 같은 MCMC 기반 추론을 사용하여 느린 반면, ProdLDA는 PyTorch 또는 Tensorflow 등 딥러닝 프레임워크 안에서 훨씬 빠르게 실행할 수 있음
○ 장점 2. LDA는 topic-word 분포를 mixture 모델로 구현하는 반면 ProdLDA는 여러 topic의 곱셈 형태로 구현하여 word distribution이 매우 뚜렷하게 나옴 (∵ 하나라도 0이 섞여 있으면 그것의 곱은 0일 것이기 때문)
○ 장점 3. ProdLDA는 가우시안 분포를 따르는 z로부터 합이 1이고 non-zero entry를 가지는 p를 생성하는데 (cf. p = Softmax(z)), 이 때문에 임베딩 공간에 있는 pre-trained embedding, graph feature 등을 함께 활용할 수 있음
⑥ Python 프로그래밍 : sklearn.decomposition.LatentDirichletAllocation
from sklearn.decomposition import LatentDirichletAllocation
lda = LatentDirichletAllocation(n_components=10, random_state=0)
spotwise_celltype_probability.shape
# (10000, 14)
theta = lda.fit_transform(spotwise_celltype_probability)
print(theta.shape)
# (10000, 10)
beta = lda.components_
print(beta.shape)
# (10, 14)
⑷ 4-4. CountClust (Dey et al., 2017)
⑸ 4-5. FastTopics (Carbonetto et al., 2023)
6. 종류 5. 생성적 적대 신경망(GAN, generative adversarial network) [목차]
⑴ 개요
① 서로 경쟁하는 두 개의 신경망을 구현
② 경쟁 관계자 : 생성자(generator), 감별자(적대자, discriminator, adversary)
③ 학습 과정 : 생성자는 점점 실제 같은 이미지를 생성하고, 감별자는 진짜와 가짜를 점점 잘 구별
④ 비지도 학습
Figure. 2. GAN 모식도
⑵ 생성자(G) 모델
① 역할 : 임의의 n차원 데이터(잡음)를 입력받아 이미지 생성
○ 예 : 28 × 28 × 1 흑백 이미지
② 옵티마이저 : 감별자 옵티마이저와 공통으로 사용하지 않도록 별도 생성
③ 손실함수
○ 목표 : 가짜 이미지를 만들었는데, 판별자(D)가 그걸 진짜(1) 라고 판단하게 만들기
○ BCE(binary cross entropy)를 이용해 모든 값이 1인 행렬과 감별자의 결과 행렬과 손실 계산
○ LG = BCE(1, D(G(z)))
⑶ 감별자(D) 모델
① 역할 : 생성자가 생성한 이미지를 입력받아 진짜와 가짜를 이분법으로 분류
○ 예 : sigmoid 확률
② 옵티마이저 : 생성자 옵티마이저와 공통으로 사용하지 않도록 별도 생성
③ 손실 함수 : 두 개의 손실함수의 합
○ 목표 : 진짜 이미지는 진짜(1) 로 맞히고 생성자가 만든 가짜 이미지는 가짜(0) 로 맞히기
○ 진짜 이미지에 대한 손실 LD,real = BCE(1, D(x))
○ 가짜 이미지에 대한 손실 LD,fake = BCE(0, D(G(z)))
○ 최종 D 손실함수 LD = LD,real + LD,fake
7. 종류 6. flow mdel [목차]
⑴ XVFI : optical flow 일종
⑵ FILM(Frame Interpolation for Large Motion) : 인코더 + U-Net like decoder
입력: 2023.06.27 00:55
수정: 2025.06.22 18:49
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 8강. 클러스터링 알고리즘 (0) | 2023.09.22 |
|---|---|
| 【알고리즘】 13강. 앙상블 학습 (0) | 2023.06.27 |
| 【알고리즘】 17강. RNN 알고리즘 (0) | 2023.06.27 |
| 【알고리즘】 21-1강. 프롬프트 엔지니어링 (0) | 2023.04.03 |
| 【알고리즘】 21강. 거대 언어 모델(LLM) (0) | 2023.03.31 |
최근댓글