그래프 이론(graph theory)
추천글 : 【현대수학】 현대수학 목차
1. 기초 [본문]
2. 응용 [본문]
1. 기초 [목차]
⑴ 그래프의 구성 요소
① V : 노드(정점, vertex)
② E : 엣지(간선, edge)
③ G : 그래프
④ V(G) = {v1, ···, vn}
⑤ vi ~ vj : 엣지 eij가 vi, vj를 연결하는 경우
⑵ 그래프 G의 차수 : 노드의 개수, 즉 |V(G)|
⑶ 그래프 G의 크기 : 엣지의 개수, 즉 |E(G)|
⑷ 노드 vi의 차수(degree) : 노드 vi에 연결된 엣지의 개수, 즉 deg(vi)
① deg(vi) = ∑vi~vj 1
② δ(G)는 G의 노드의 차수 중 최솟값을, Δ(G)는 G의 노드의 차수 중 최댓값을 지칭
③ ∑ deg(vi) = 2 | E(G) |
④ regular : 그래프 내 모든 노드의 차수가 동일한 경우
⑤ Eulerian graph : 그래프 내 모든 노드의 차수가 짝수인 경우
⑸ 그래프의 종류
① 단순그래프(simple graph) : 두 노드 사이에 최대 한 엣지만 존재하며, 한 노드가 자기 자신과 연결되는 루프는 허용되지 않는 그래프
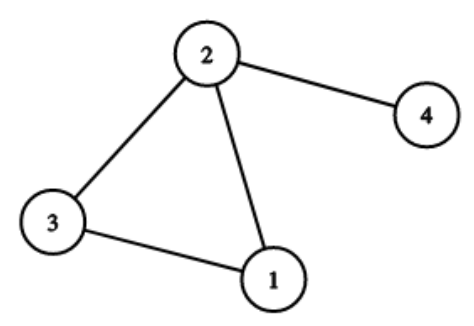
Figure. 1. 단순그래프
② 완전그래프(complete graph) : 그래프의 모든 노드쌍이 유일한 엣지로 연결돼 있는 그래프

Figure. 2. 완전그래프
○ strongly connected (= irreducible) : 그래프 내 임의의 노드 i에서 다른 임의의 노드 j로 도달할 수 있는 상태
○ 완전그래프를 구성하는 엣지의 수는 NC2 = N(N-1) / 2
⑹ 서브그래프(subgraph) : V(H) ⊆ V(G)이고 E(H) ⊆ E(G)인 그래프 H
① induced subgraph : G에서는 존재하지 않는 간선이 H에 새롭게 생기지 않는, 서브그래프 H
② clique : 서브그래프가 완전그래프인 경우
③ walk : v0v1, v1v2, ···, vm-1vm 엣지들로 연결된 v0 → v1 → ··· → vm와 같은 경로
○ v0를 initial vertex라고 하고, vm을 final vertex라고 함
○ walk를 구성하는 엣지의 개수를 length라고 함
④ path : 노드가 모두 고유한 walk
⑤ cycle : v0 = vm인 walk. 즉 모든 노드가 2개의 이웃을 가지는 clique
⑥ forest : 사이클을 포함하지 않는 그래프
⑦ tree : connected forest
⑧ period : 특정 노드 i의 period는 노드 i에서 i로 향한는 모든 path의 최대공약수
○ 예 : 두 개의 노드 A, B가 있고 A=B와 같이 두 개의 엣지로 연결돼 있으면 각 노드의 period는 2
⑨ aperiodic : 모든 노드의 period가 1인 것
○ aperiodic ⊂ irreduicible
○ 예 : 각 노드가 자기 자신으로 향하는 walk가 있으면 aperiodic
⑩ regular
○ regular ⊂ irreduicible
○ 어떤 자연수 k에 대해, transition matrix M의 거듭제곱 Mk의 모든 원소가 양수(즉, 0이 아닌 값)인 경우
⑺ 그래프의 종류
① undirected graph : 그래프의 엣지가 방향성이 없는 경우
② directed graph : 그래프의 엣지가 특정 방향성이 있는 경우
③ k-partite : 노드의 집합을 k개의 그룹으로 나눌 수 있고, 같은 그룹에 속한 노드들이 서로 인접하지 않을 때
⑻ 네트워크의 중심성(centrality)
① degree centrality : 사회적 커넥션이 많은 사람들을 보여줌
② closeness centrality : 소셜 네트워크의 중심이 누구인지를 나타냄
③ betweenness centrality : social circle에 연결된 사람들을 나타냄
④ eigenvector centrality : 네트워크에서 영향력 있는 사람들을 나타냄
⑼ 인접행렬(adjancy matrix) : A로 표시
① 정의 : 노드의 개수를 n이라 할 때 n × n 인접행렬은, Ai,j = 1 (if vi ~ vj), Ai,j = 0 (otherwise)로 정의
Figure. 3. 인접행렬의 예시
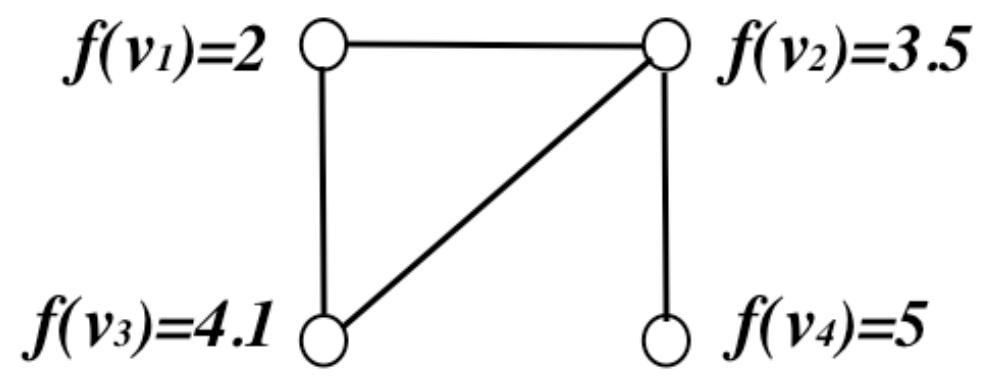
② 각 노드와 실수값을 연결하는 함수 f
Figure. 4. 함수 f의 예시
③ 다음 관계식이 성립함
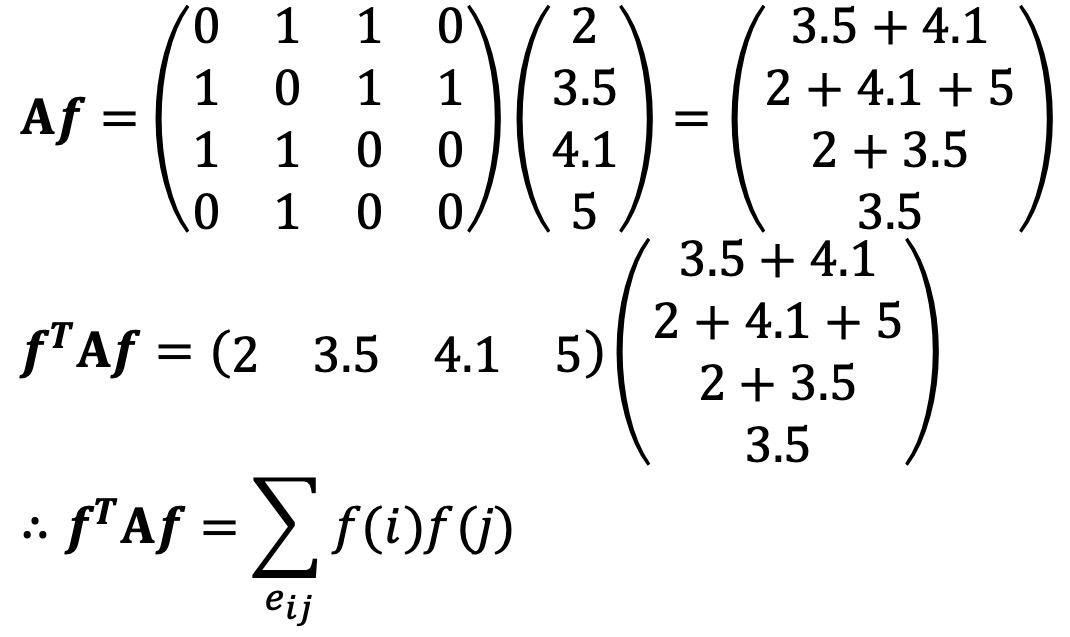
④ symmetrically normalized adjacency matrix : Ã = D-1/2AD-1/2 (단, Dii = d(vi))
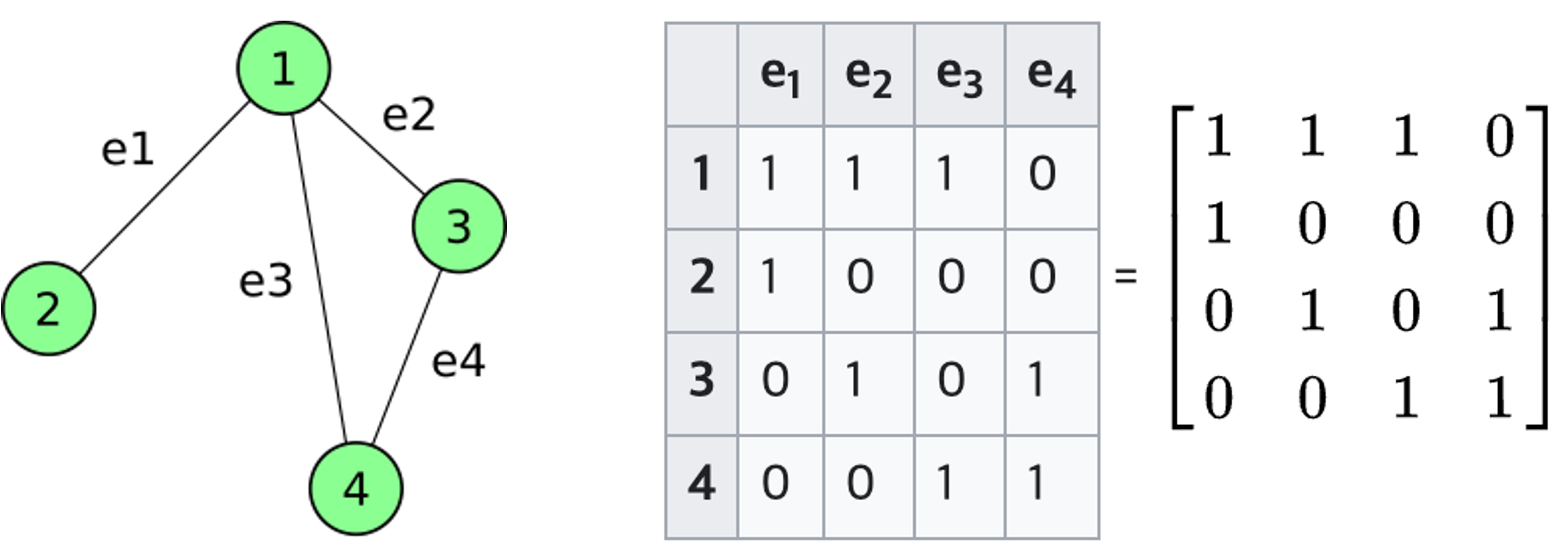
⑽ 근접행렬(사건행렬, incidence matrix) : ∇로 표시
① undirected graph의 근접행렬 : Bi,j = 1 (if vertex vi is incident with edge ej), Bi,j = 0 (otherwise)로 정의
Figure. 5. 근접행렬 예시
② directed graph의 근접행렬

③ 노드가 행, 엣지가 열인 경우(예 : Fig. 5)와 엣지가 행, 노드가 열인 경우(예 : Fig. 6)가 모두 사용되고 있음
⑾ 라플라스 행렬(Laplacian matrix)
① 개요
○ 정의 : L = ∇T∇ = D - A (단, Dii = d(vi))
○ multiplicity : 연속적인 서브그래프의 개수
Figure. 6. 라플라스 행렬 예시
○ 위의 경우 ∇는 다음과 같음
Matrix([
[1, -1, 0, 0], # e1: v1 -> v2
[1, 0, -1, 0], # e2: v1 -> v3
[0, 1, -1, 0], # e3: v2 -> v3
[0, 1, 0, -1] # e4: v2 -> v4
])
② 라플라스 행렬의 변형
○ normalized graph Laplacian : Ln = D-1/2LD-1/2 = I - D-1/2AD-1/2. symmetric, semi-definite positive
○ Markov chain의 전이 행렬(transition matrix) : Lt = D-1A
○ random-walk graph Laplacian : Lr = D-1L = I - Lt = D-1/2LnD1/2
③ 특징 1. L은 고유치 0을 가지고 있음 : L1n = 0
○ k개의 분리된 그래프가 있으면 0의 고유값이 k개가 존재함
○ 고유값이 0에 가까울수록 그래프가 더 잘 연결되어 있음을 나타냄
○ Fiedler 벡터 : λ1 = 0 다음으로 두 번째로 작은 고유값에 대응하는 고유벡터. 그래프의 전체적인 구조를 나타냄
④ 특징 2. Laplacian as an operator
○ (Lf)(vi) = ∑vj~vi (f(vi) - f(vj)) : Fig. 4 참고
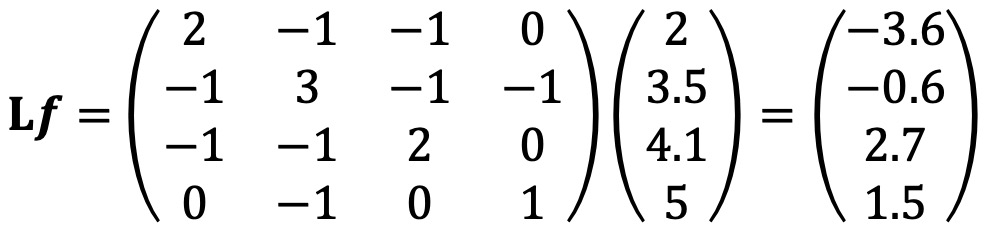
⑤ 특징 3. L은 대칭이고 양반정부호 행렬(positive semi-definite matrix)
○ 2차 형식 : fTLf = ∑ei,j, i < j (f(vi) - f(vj))2 = (1/2) ∑ei,j (f(vi) - f(vj))2 ≥ 0
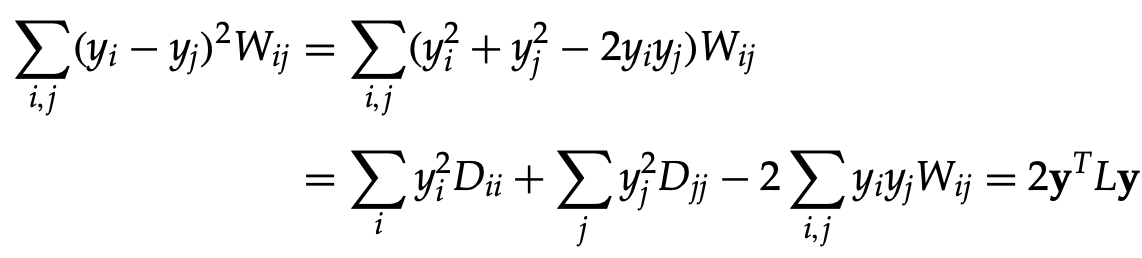
○ Fig. 4의 예시에서 fTLf = 9.27
○ 즉, L의 모든 고유치가 0보다 크거나 같은 실수
⑥ 특징 4. Y = [y1 y2 ⋯ ym] ∈ ℝk×m에 대하여
○ tr(YTLY) = ∑ei,j || yi - yj ||2
⑦ 특징 5. Rayleigh quotient
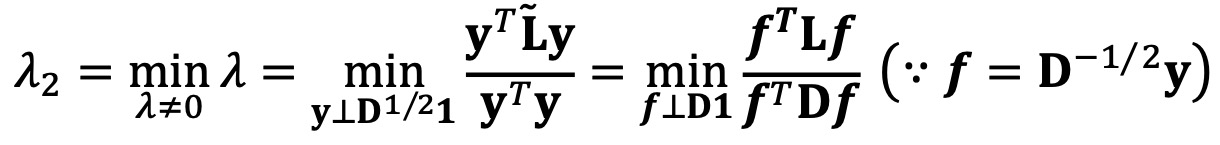
○ λ2 = Fiedler 값(algebraic connectivity)은 값을 차이나게 하는데 필요한 에너지를 의미함
○ 이 값이 크면 데이터들을 분리하는 게 어려워 전체적으로 잘 연결된 구조가 됨
○ 이 값이 작으면 데이터들을 분리하는 게 쉬워 약하게 연결된 구조, 별도의 클러스터로 군집화된 구조를 의미함
⑧ 응용 1. undirected weighted graph에서의 라플라시안 연산
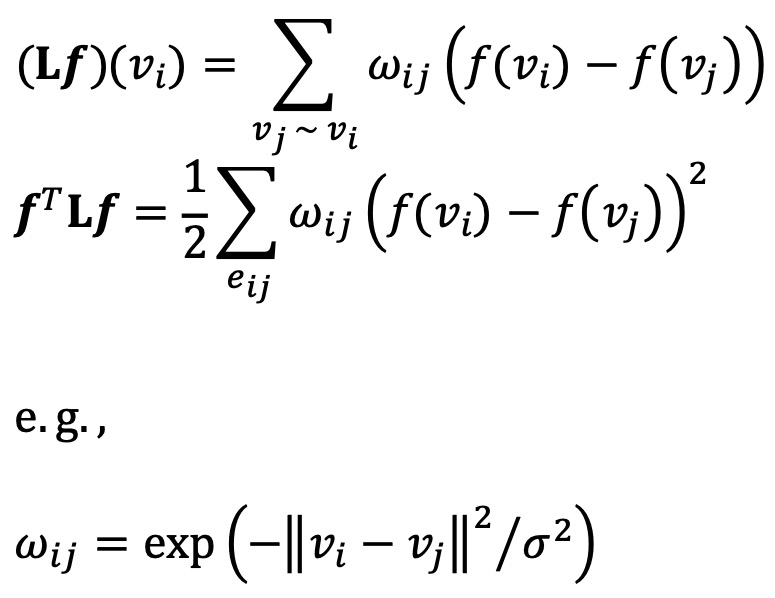
⑨ 응용 2. spectral clustering (ref)
○ 원래 문제
○ 정의 : 그래프에서 최소 컷(min-cut)을 찾는 것. 클러스터 간 엣지 가중치는 최소화하면서, 클러스터 volume은 정규화된 분할
○ cut의 정의
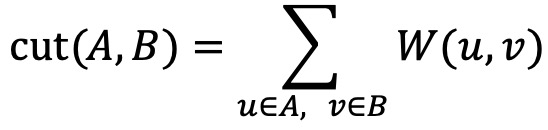
○ volume의 정의
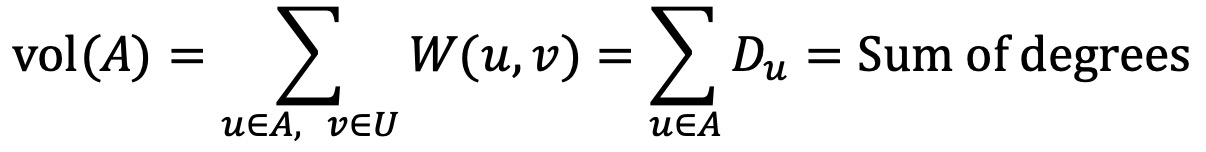
○ 2-cluster optimization problem
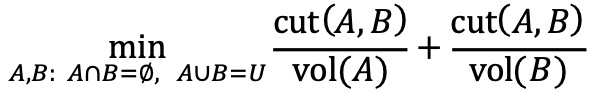
○ multi-cluster optimization problem
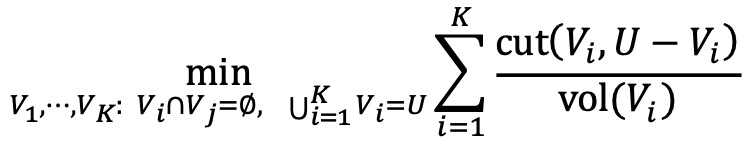
○ spectral clustering은 다음과 같은 클러스터 레이블의 one-hot encoding X ∈ {0, 1}N×K를 찾는 것과 동일함
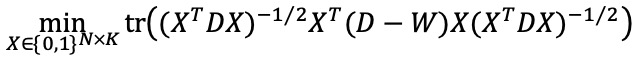
○ 라플라시안 행렬을 이용한 풀이
○ 문제 정의
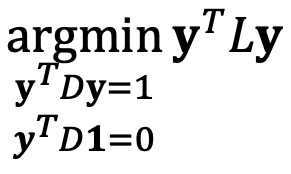
○ yTDy = 1 조건이 필요한 이유 : 이 조건이 없으면 자명한 해 y = 0가 존재하고, 임의의 y ≠ 0에 대해서 목적함수의 값을 작게 만드는 cy, 0 ≤ c < 1이 존재함
○ yTD1 = 0 조건이 필요한 이유 : 이 조건은 y ≠ 1과 필요충분조건 (orthogonality). 이 조건이 없으면 목적함수의 최솟값은 언제나 0이고 언제나 y = 1 (∵ 라그랑주 승수법)
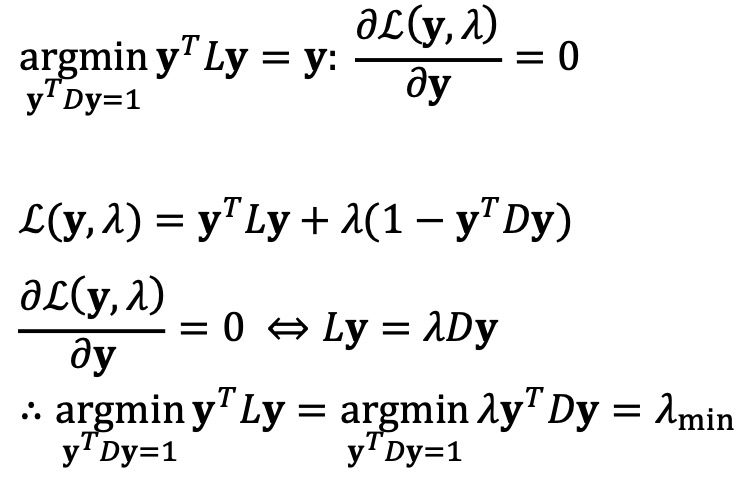
○ 원래 spectral clustering 문제에서 one-hot constraint를 완화하고 XTDX = I 조건을 추가하면 이 풀이와 동일해짐
○ 단계 1. 주어진 n개의 데이터 포인트들 사이의 거리를 계산하여 n × n 크기의 인접 행렬 A를 만듦. 가우시안 커널을 많이 이용
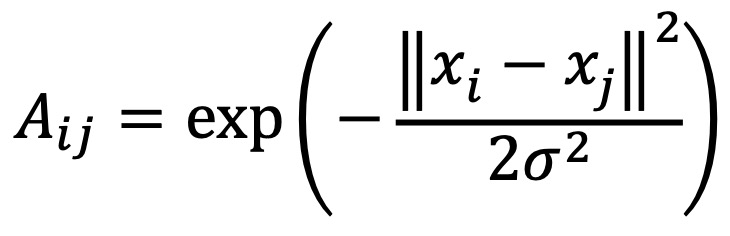
○ 단계 2. 인접 행렬을 기반으로 Laplacian 행렬을 계산 : Ln 혹은 Lr도 사용됨
○ 단계 3. Laplacian 행렬의 가장 작은 k개의 고유값과 대응되는 고유 벡터 행렬 W = [ω2, ···, ωk] ∈ ℝn×k를 계산. λ1 = 0에 대응되는 ω1 = 1은 자명하므로 제외
○ 단계 4. n개의 데이터는 k차원으로 자연스럽게 임베딩됨 : Y = WT = [y1, ⋯, yn]의 각 열벡터
○ 단계 5. Y의 열벡터를 K-means clustering 등으로 클러스터링 수행
⑿ 차수 분포(degree distribution) : 전체 노드 중 차수가 k인 노드의 비율, 즉 P(k) = Nk / |V(G)|
⒀ 거리(distance) : 두 노드를 연결하는 가장 짧은 path의 길이. 그러한 path가 존재하지 않으면 거리는 ∞으로 정의
⒁ 클러스터링 계수(clustering coefficient) : 특정 노드의 차수를 ki라고 하고, 그 노드와 연결된 주변 노드들끼리 연결된 엣지의 수를 ei라 할 때
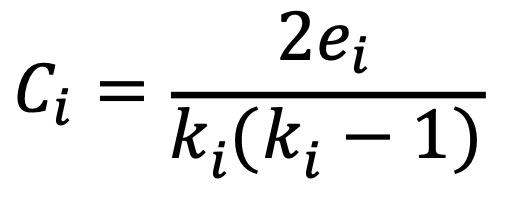
① 예를 들어, A가 B, C, D와 연결돼 있고, B-C, C-D 엣지가 추가로 있을 때, A에 대하여 ei = 2, ki = 3, Ci = 2 / 3
② ki (ki - 1) / 2 : 주변 노드들끼리 만들 수 있는 최대 엣지 개수
③ Ci는 0에서 1 사이의 값을 가지며, 1에 가까울수록 해당 노드의 주변 노드들이 완전히 연결된 것을 의미함
2. 응용 [목차]
⑴ 비둘기집의 원리
⑵ 노드의 개수에 따른 고유한 그래프의 개수 : 거의 완벽하게 지수함수를 따름
⑶ 다익스트라(Dijkstra) 및 Floyd 알고리즘
⑸ 신념의 힘
⑹ 사회적 네트워크 이론 혹은 six degress of separation
① 지구상의 임의의 두 사람을 골라도 최대 여섯 명만 건너면 아는 사이라는 것
② 증명 : 한 명이 평균 100명을 안다고 했을 때, 여섯 번을 건너면 1006 = 10억 명이 되어 비슷한 결론이 나옴
⑺ Perron-Frobenius theorem
① 정리 1. transition matrix가 P인 Markov chain이 strongly connected이면 오직 1개의 정상상태 분포 q가 존재
○ 정상상태 분포는 Pq = q를 만족함
② 정리 2. transition matrix가 P인 Markov chain이 strongly connected이고 aperiodic이면,
○ Pij : 노드 j에서 노드 i로 전이될 확률. ∑i Pij = 1
○ 2-1. Pk의 i행 j열 원소 Pij(k)는 k → ∞로 갈 때 qi로 수렴 : 이때 i만 같으면 j와 무관하게 같은 값으로 수렴함을 주목
○ 2-2. 초기상태 x0에 무관하게 k번째 상태 xk는 k → ∞로 갈 때 q로 수렴
⑻ 구글의 page rank 알고리즘
① 단계 1. 웹페이지들을 그래프로 나타내고, 이를 Markov process transition matrix P로 표현
② 단계 2. sink 노드의 경우 다른 페이지로의 transition 확률을 1/n로 강제로 할당 : P → P'
③ 단계 3. P'' = (1 - α) P' + (α / n) 1
○ 단, 1은 n × n에 1이 모두 채워진 형태
○ P'은 regular하다는 보장은 없지만, P''은 언제나 regular함이 보장됨
○ P''은 구글의 창업자 세르게이 브린과 래리 페이지가 정의한 Markov chain
④ 단계 4. P''x = x인 steady-state vector x를 탐색
○ P''은 regular하므로 strongly connected이고, 이로 인해 steady-state가 유일하게 존재함
○ 이때의 state-transition probability가 추천된 페이지의 중요도라고 할 수 있음
⑼ 4색 정리(four color theorem)
① 인접한 두 지역이 같은 색을 가지지 않도록 하기 위한 어떤 지도도 최대 4가지 색만으로 색칠할 수 있음
② 컴퓨터를 통해 모든 경우에서 4색 정리가 성립함을 확인함으로써 증명함
⑽ 한붓그리기 문제 혹은 쾨니히스베르크 다리 문제(Königsberg bridge problem)
① 어떤 그래프에서 각 노드를 한 번씩만 지나는 Eulerian path가 존재하려면 차수가 홀수인 노드가 0개이거나 2개여야 함
② 차수가 홀수인 노드가 2개이면 홀수 차수를 가진 두 노드 중 하나는 출발점, 다른 하나는 도착점이 됨
③ 쾨니히스베르크의 7개의 다리를 한 번씩만 모두 건너는 경로는 존재하지 않음
⑾ 램지 이론(Ramsey theory)
① 충분히 큰 그래프에는 반드시 특정한 구조(예 : 아는 사람들로 이루어진 완전 그래프, 모르는 사람들로 구성된 부분 그래프)가 존재함
② R(s, t) : s명의 모르는 사람들로 구성된 서브그래프 혹은 t명의 아는 사람들로 구성된 서브그래프가 반드시 존재하는 최소 노드 수
③ 정리 1. R(3, 3) = 6 : 임의의 6명 중에서는, 서로 친구인 3명이 있거나, 서로 친구가 아닌 3명이 존재. 경우의 수로 증명할 수 있음
④ 정리 2. R(3, 3, 3) = 17
⑤ 정리 3. R(3, 3, 4) = 30
⑥ 정리 4. R(s, t)의 점화식 : R(s, t) ≤ R(s-1, t) + R(s, t-1)
⑦ 정리 5. R(s, t)의 상한의 존재성 : R(s, t)의 점화식 및 수학적 귀납법으로 증명 (ref)
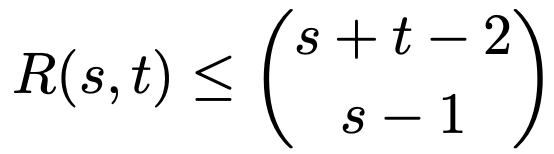
⑧ 정리 6. Rk(s1, s2, ···, sk) ≤ Rk/2(R(s1, s2), R(s3, s4), ···, R(sk-1, sk))
⑾ 슐의 정리(Schur's theorem)
① 임의의 k ≥ 2에 대하여, k-coloring 하에서 같은 색으로 칠해지고 x + y = z를 만족하는 (x, y, z)를 언제나 찾을 수 있는 {1, 2, ···, n}, n > 3이 존재한다는 정리. 램지 이론을 통해 증명
② 이를 페르마의 마지막 정리와 연결시켜, xm + ym = zm (mod p)인 (x, y, z)의 존재성을 밝힘
⑿ 에르되시-레니 무작위 그래프(Erdős–Rényi Random Graph)
① 무작위로 노드를 연결하는 단순한 규칙으로도 일정 임계점에서부터 매우 큰 그래프가 생성
입력: 2024.10.01 19:44
'▶ 자연과학 > ▷ 현대수학' 카테고리의 다른 글
| 【현대수학】 군 이론 (Group Theory) (0) | 2024.12.22 |
|---|---|
| 【현대수학】 현대수학 목차 (0) | 2016.06.25 |
| 【현대수학】 수학 난제 리스트 (0) | 2016.06.24 |

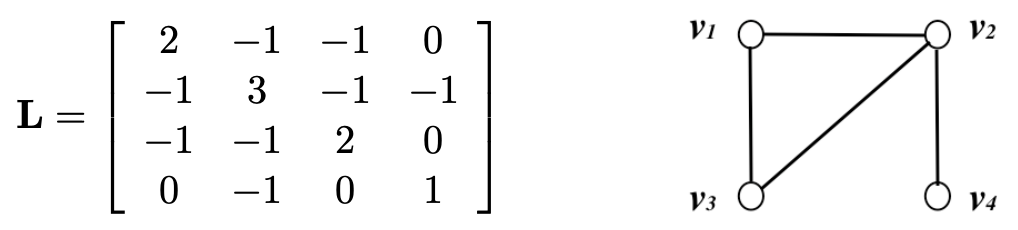



최근댓글