알케인의 구조이성질체와 그래프 이론
추천글 : 【유기화학】 4강. 입체화학, 【그래프 이론】 그래프 이론
Q. 문제
C3H8부터 C20H42까지의 구조 이성질체의 개수를 조사하고 그 추이를 분석하여라.
즉, 전체 노드의 개수가 n이고 각 노드별 최대 연결의 개수가 4개일 때, 구조적으로 구별되는 네트워크의 개수를 구하는 문제이다.
A. 풀이
탄소 수에 따른 알케인의 구조이성질체 모두 그리는 코드는 다음과 같다. 이를 응용하여 쉽게 구조이성질체의 수도 구할 수 있다.
from rdkit import Chem
from rdkit.Chem import Draw
from rdkit.Chem import AllChem
from rdkit.Chem.rdchem import Mol
from IPython.display import display
def generate_alkanes(n_carbons):
if n_carbons == 1:
return [Chem.MolFromSmiles('C')]
elif n_carbons == 2:
return [Chem.MolFromSmiles('CC')]
smaller_alkanes = generate_alkanes(n_carbons - 1)
new_alkanes = set()
for mol in smaller_alkanes:
for atom in mol.GetAtoms():
if atom.GetDegree() < 4: # 탄소는 최대 4개의 결합을 가질 수 있음
new_mol = Chem.RWMol(mol)
new_idx = new_mol.AddAtom(Chem.Atom(6))
new_mol.AddBond(atom.GetIdx(), new_idx, Chem.BondType.SINGLE)
Chem.SanitizeMol(new_mol)
smiles = Chem.MolToSmiles(new_mol, canonical=True)
new_alkanes.add(smiles)
return [Chem.MolFromSmiles(smiles) for smiles in new_alkanes]
# C7H16의 모든 구조 이성질체 생성 및 시각화
n_carbons = 7
alkanes = generate_alkanes(n_carbons)
img = Draw.MolsToGridImage(alkanes, molsPerRow=5, subImgSize=(200, 200))
# 이미지를 직접 디스플레이 (Jupyter 노트북에서만 동작)
display(img)
⑴ C4H10의 구조이성질체 (2개)

⑵ C5H12의 구조이성질체 (3개)
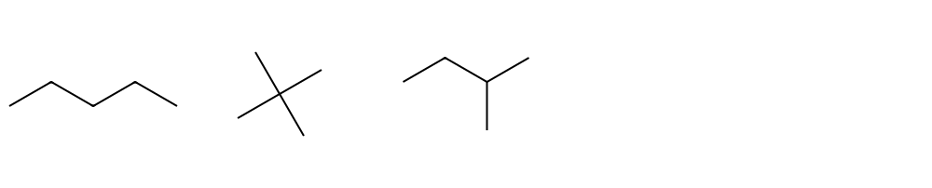
⑶ C6H14의 구조이성질체 (5개)
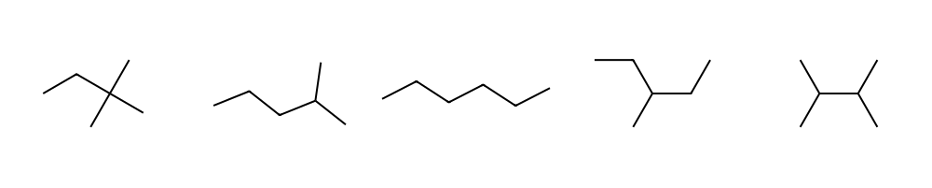
⑷ C7H16의 구조이성질체 (9개)
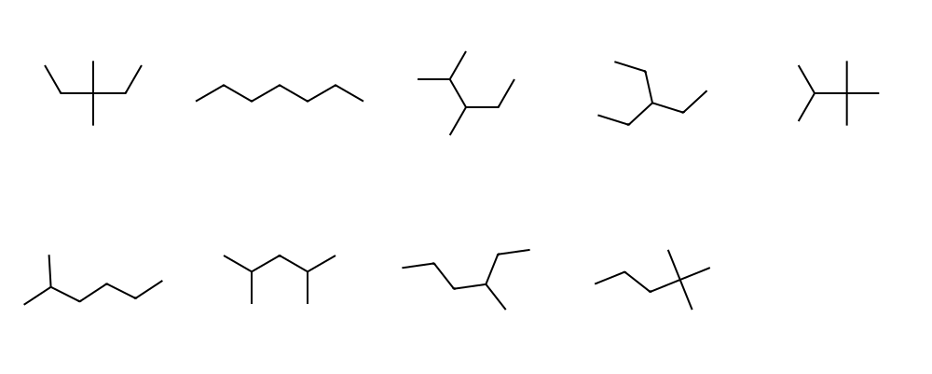
⑸ C8H18의 구조이성질체 (18개)
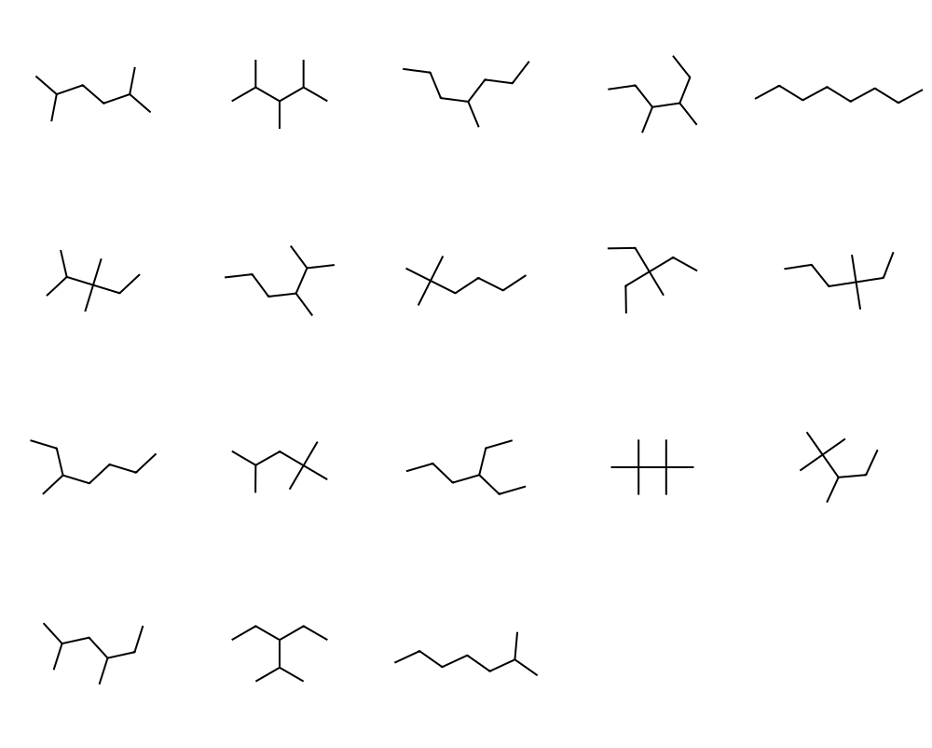
⑹ C9H20의 구조이성질체 (35개)

⑺ C10H22의 구조이성질체 (75개)


다음은 탄소 수에 따른 구조이성질체의 수이다.
| 화학식 | 구조이성질체의 수 |
| C3H8 | 1 |
| C4H10 | 2 |
| C5H12 | 3 |
| C6H14 | 5 |
| C7H16 | 9 |
| C8H18 | 18 |
| C9H20 | 35 |
| C10H22 | 75 |
| C11H24 | 159 |
| C12H26 | 355 |
| C13H28 | 802 |
| C14H30 | 1,858 |
| C15H32 | 4,347 |
| C16H34 | 10,359 |
| C17H36 | 24,894 |
| C18H38 | 60,523 |
| C19H40 | 148,284 |
| C20H42 | 366,319 |
| C30H62 | 4,111,846,763 |
| C40H82 | 62,481,801,147,341 |
Table. 1. 탄소 수에 따른 알케인의 구조이성질체의 수
다음은 탄소 수에 따른 알케인의 구조이성질체의 수의 추이이다.
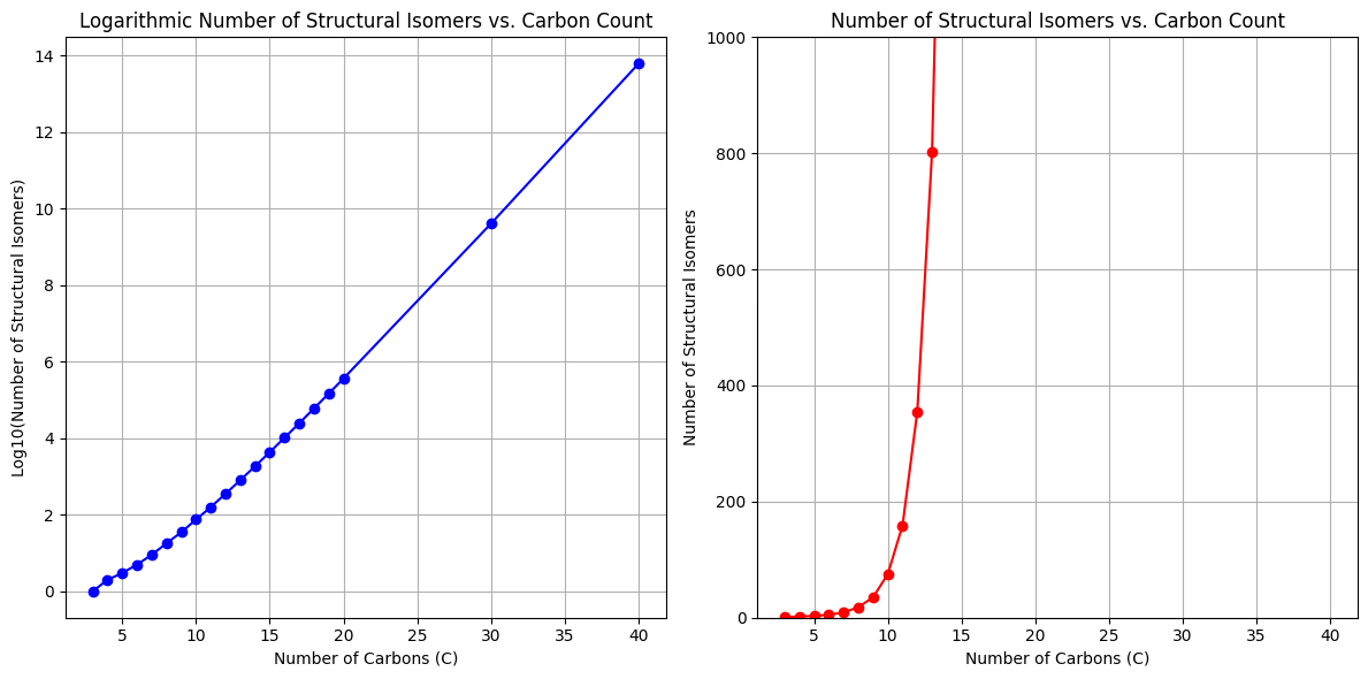
구조이성질체의 수를 로그 취하고, 탄소 수에 대하여 선형회귀 분석을 하면 다음과 같은 식을 구할 수 있다.
log10 (구조이성질체의 수) = 0.3723 × 탄소 수 - 1.7067
따라서 탄소 원자의 수가 1개 증가할 때마다 구조이성질체의 수는 100.3723 = 2.36배 증가한다는 결과를 얻었다. 최대 결합수가 3인 경우에는 이보다 낮은 약 1.91배 정도 증가했으며 (C3 ~ C20 구간에서 계산), 최대 결합수가 2인 경우 구조이성질체의 수는 항상 1로 일정하다. 이로 인해 구조이성질체의 수를 정확하게 표현하는 수식은 아직 발견되지 않았지만, 구조이성질체의 수가 분명히 등비수열을 따르고 있으며, 그 등비는 원자의 최대 결합수가 증가함에 따라 증가한다는 것을 알 수 있다. 이를 이해하기 위해 탄소 원자의 수를 n, 구조이성질체의 수를 f(n)이라 두고, 다음과 같은 점화식을 분석해 보자.
f(n) × n / (대칭성에 의한 중복) – g(n) = f(n+1) × (평균적인 말단 탄소 개수)
○ f(n) × n / (대칭성에 의한 중복)은 탄소 수가 n인 모든 구조이성질체의 각 탄소에 새로 탄소를 1개 연결한 경우를 의미한다. 이때, 180°, 120° 대칭성 등에 의해 중복된 구조가 발생하는데, n이 커질수록 180° 대칭성이 주로 나타나므로 (대칭성에 의한 중복)이 2로 수렴한다.
○ g(n)은 f(n)의 모든 4차 탄소 개수를 나타낸다. 한 분자 내에도 2개 이상의 4차 탄소가 있을 수 있다. 여기에 추가적인 탄소가 연결되면 5차 탄소가 되어 옥텟 규칙을 위반하게 되므로, 이는 경우의 수 계산에서 제외하여야 한다. 그리고 최대 결합수가 4가 아닌 경우, g(n)의 정의는 최대 결합수를 가지는 탄소 개수를 의미하는 것으로 해석한다.
○ f(n+1) × (평균적인 말단 탄소 개수)는 n+1개의 탄소를 가진 각 구조 이성질체에서 f(n)을 기반으로 새롭게 형성될 수 있는 말단 탄소의 평균 개수를 나타낸다. 최대 결합수가 적어지면 평균적인 말단 개수가 줄어들며, 극단적으로는 최대 결합이 2인 경우 말단 개수는 언제나 2개이다 (e.g., C-C-C).
탄소 수가 충분히 많을 경우, (대칭성에 의한 중복)은 2로 수렴하고, g(n)은 f(n) × n / (대칭성에 의한 중복)에 비해 충분히 작아지며 (단, 최대 결합수가 2인 경우 g(n)을 무시할 수 없다), 전체 탄소 중 말단 탄소의 비율은 대체로 일정하게 유지될 것이라는 것을 직관적으로 이해할 수 있다. (평균적인 말단 탄소 개수)가 전체 탄소 중 20% 정도라고 가정하면, f(n+1) / f(n)의 비율이 왜 일정하게 유지되는지 이해할 수 있다.
f(n+1) / f(n) ≃ n / [(대칭성에 의한 중복) × (평균적인 말단 탄소 개수)] = 2.5
입력: 2024.06.20 10:13
'▶ 자연과학 > ▷ 유기화학' 카테고리의 다른 글
| 【유기화학】 유기화학 목차 (149) | 2024.12.27 |
|---|---|
| 【유기화학】 28강. 분광학 (4) | 2024.12.27 |
| 【유기화학】 11-1강. 방향족성 판단 예제 (2) | 2024.05.28 |
| 【유기화학】 혼성효과와 산도 비교 예제 (2) | 2024.05.19 |
| 【유기화학】 1-1강. 물리화학적 성질 예제 (6) | 2024.03.26 |



최근댓글