수학 난제 리스트
추천글 : 【현대수학】 현대수학 목차
1. 미해결 난제 [본문]
2. 해결 난제 [본문]
a. 수학 탐구 주제 리스트
1. 미해결 난제 [목차]
⑵ 3n+1 문제 : 어떤 수 n이 짝수일 경우 n을 2로 나누고, 홀수일 경우 3n+1로 변환할 때, 이 수열이 결국 1로 수렴한다는 것을 증명
⑶ P 대 NP 문제
① 용어
○ 결정론적 알고리즘 : 계산의 각 단계에서 단 한 가지의 가능성만을 고려하는 알고리즘
○ 비결정론적 알고리즘 : 계산의 각 단계에서 2가지 이상의 가능성만을 고려하는 알고리즘
○ 비결정론적 알고리즘은 이론적인 개념으로, 실제 컴퓨터에서 구현할 수 없음
○ 각 단계에서 여러 가능한 경로를 동시에 고려할 수 있으며, 이 중 올바른 경로를 "운 좋게" 선택한다고 가정
○ 각 단계에서 모험가가 분신술을 써서 최적의 경로를 탐색하는 것을 생각할 수 있음 (ref)
○ 모험가에게 분신술의 능력이 없어도 매 지점마다 누군가가 어느 길목으로 가라는 힌트를 주었고 그 힌트를 검증할 수 있다면 동일하게 최적 경로를 탐색할 수 있음 (ref)
○ 그러므로 비결정론적 알고리즘은 다항 시간에 어떤 힌트를 검증하는 결정론적 알고리즘과 동일하다고 할 수 있음
○ P 문제 := 결정적 알고리즘으로 다항시간 내에 해결할 수 있는 문제
○ 문제를 풀지 못했다는 것을, 결정적 알고리즘으로 다항 시간 내에 해결할 수 없다는 의미로 본 것
○ NP 문제 := 비결정적 알고리즘으로 다항시간 내에 해결할 수 있는 문제 = 결정적 알고리즘으로 다항시간 내에 검증할 수 있는 문제
○ NP 난해(NP hard) : NP에 속하는 모든 문제에 대해 다른 문제로 polynomial-time many-one reducible되는 문제 (ref)
○ NP 문제를 더 어렵게 만든 문제라고 할 수 있음
○ NP 완전(NP complete) : 문제 A가 NP에 속하며,동시에 NP에 속하는 모든 문제에 대해 polynomial-time many-one reducible되는 문제들의 집합 (ref)
② 정의
○ 결정적 알고리즘 ⊂ 비결정적 알고리즘이므로 (e.g., 각 단계에서 1개의 옳은 선택과 1개의 무작위 선택), P 문제 ⊂ NP 문제가 성립
○ P 대 NP 문제는 NP 문제가 P 문제와 동일한지, 더 많은 원소를 가지는지, 그것조차 증명할 수 없는지를 증명해야 함
○ NP 문제 = (P 문제) + (NP-완전 문제) + (P≠NP라면 NP-완전 문제가 아닌 NP 문제)
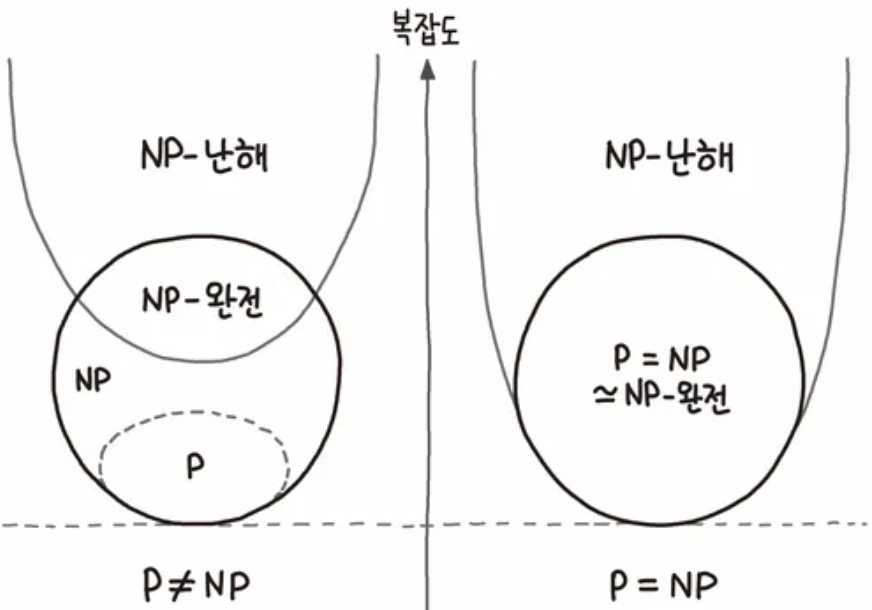
Figure. 1. P 대 NP 문제
③ 예시
○ 두 도시 간 최단 경로 문제 : P 문제. 다익스트라(Dijkstra), Floyd 알고리즘 등으로 풀림
○ 최대 공약수 계산 문제 : P 문제. 유클리드 호제법으로 풀림
○ 정렬 문제 : P 문제. 버블 정렬, 퀵 정렬 등으로 풀림
○ 소인수 분해 : NP-완전 문제인지 아닌지 혹은 증명할 수 없는지 증명되지 않았음
○ 여행자 문제(TSP, traveling salesman problem) : NP-complete 문제. 여러 도시와 각 도시 간의 거리가 주어져 있을 때, 모든 도시를 한 번씩 방문하고 출발지로 돌아오는 경로 중 가장 짧은 경로를 찾는 것
○ fragment orientation problem (FOP) : NP-complete. 생물정보학에서 DNA 조각의 방향을 올바르게 정하는 문제
○ 슈퍼 마리오브라더스 : NP-hard
⑷ 리만 가설
⑸ 삼각화단 문제
⑹ 알케인의 구조 이성질체 개수를 설명하는 수학식 (ref)
⑺ kissing number : n차원 구가 (n + 1)차원 유클리드 공간에서 가질 수 있는 최대 kissing number는? AlphaEvolve가 11차원에서 더 나은 해법을 도출함
⑻ power tower에 대한 이론 : 다방면의 노력에도 불구하고 우리는 이 함수에 대해 아는 것이 거의 없다 ('오일러')
2. 해결 난제 [목차]
⑴ 페르마의 마지막 정리 : 앤드류 와일드 교수님이 증명
⑵ 푸앙카레 추측
⑶ 리드 추측
① 1968년 영국 수학자 로널드 리드가 제시한 조합론 문제
② 채색 다항식 계수의 절댓값은 증가하다가 감소할 수는 있지만 감소하다가 증가할 수는 없다는 추측
③ 채색 다항식은 어떤 그래프에서 이웃한 꼭짓점을 서로 다른 색으로 칠할 때 n개 이하의 색만 써서 칠하는 방법의 수를 나타낸 식
⑷ 로타 추측
① 1971년 미국 수학자 잔카를로 로타가 리드 추측을 일반화해 제시한 문제
② 리드 추측의 그래프뿐만 아니라 벡터 공간에 있는 유한 집합의 특성 다항식까지 포함하는 일반적인 상황으로 범위를 확장
① ㄱ자 모양으로 구부러진 복도에서 이동할 수 있는 가장 큰 소파의 면적은 얼마일까? 소파의 형태는 자유롭게 선택할 수 있다.
② 대한민국 백진언 연구원 님에 의해 24년 11월 증명됨 : 아직 검증 과정에 있음
입력 : 2022.07.07 01:32
'▶ 자연과학 > ▷ 현대수학' 카테고리의 다른 글
| 【현대수학】 군 이론 (Group Theory) (0) | 2024.12.22 |
|---|---|
| 【현대수학】 그래프 이론 (Graph Theory) (2) | 2024.10.02 |
| 【현대수학】 현대수학 목차 (0) | 2016.06.25 |



최근댓글