1강. 정렬 알고리즘(sorting algorithm)
추천글 : 【알고리즘】 알고리즘 목차
1. 개요 [본문]
2. comparison-based 정렬 알고리즘 [본문]
3. non-comparison-based 정렬 알고리즘 [본문]
4. AI-based 정렬 알고리즘 [본문]
a. 정렬 알고리즘 실험
1. 개요 [목차]
⑴ 정렬(sorting)
① 입력 : 〈x1, x2, ···, xn〉과 같이 주어진 n개의 숫자열
② 출력 : 〈x1', x2', ···, xn'〉, x1' ≤ x2' ≤ ··· ≤ xn'이고 ｛x1', x2', ···, xn'｝=｛x1, x2, ···, xn｝인 n개의 숫자열
⑵ in-place 알고리즘 : 정렬 알고리즘 실행 시 데이터 저장소를 일정한 양(O(1))만을 필요로 하는 경우
⑶ 시간복잡도 (time complexity)
① 정의 : 알고리즘을 실행하는 데 필요한 단계의 수
② 서로 다른 알고리즘의 퍼포먼스를 비교하는 데 사용됨
③ 종류 1. Θ notation
○ 정의 : 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n), n > n0인 n0가 존재하는 경우 f(n) = Θ(g(n))
○ 점근선(asymptote)의 개념과 유사함
○ 당장 가장 단순한 정렬 알고리즘인 삽입 정렬에 적용할 수 없음
④ 종류 2. Ο notation
○ 정의 : 0 ≤ f(n) ≤ cg(n), n ＞ n0인 c와 n0가 존재하는 경우 f(n) = Ο(g(n))
○ 일반적으로 상수 등을 제거하고 가장 차수가 높은 항이 무엇인지로 표시함
○ best case, worst case, average case를 상정할 수 있으나 worst case의 경우를 기준으로 함
○ 상한(upper bound)의 개념과 유사함
○ 일반적으로 가장 많이 사용됨
⑤ 종류 3. Ω notation
○ 정의 : 0 ≤ cg(n) ≤ f(n), n ＞ n0인 c와 n0가 존재하는 경우 f(n) = Ω(g(n))
○ 하한(lower bound)의 개념과 유사함
⑥ 시간 복잡도의 성질
○ f(n) = Θ(f(n))
○ f(n) = Ο(f(n))
○ f(n) = Ω(f(n))
○ f(n) = Θ(g(n))이고 g(n) = Θ(h(n))이면 f(n) = Θ(h(n))
○ f(n) = Ο(g(n))이고 g(n) = Ο(h(n))이면 f(n) = Ο(h(n))
○ f(n) = Ω(g(n))이고 g(n) = Ω(h(n))이면 f(n) = Ω(h(n))
○ f(n) = Θ(g(n))인 것과 g(n) = Θ(f(n))인 것은 필요충분조건
○ f(n) = Ο(g(n))인 것과 g(n) = Ω(f(n))인 것은 필요충분조건
○ f(n) = O(g(n))도 아니고 f(n) = Ω(g(n))도 아닌 예 : f(n) = n이고 g(n) = n1+sin n
2. comparison-based 정렬 알고리즘 [목차]
⑴ 개요
| worst case | best case | in-place 여부 | |
| 버블 정렬 | O(N2) | O(N2) | Yes |
| 삽입 정렬 | O(N2) | O(N) | Yes |
| 선택 정렬 | O(N2) | O(N2) | Yes |
| 병합 정렬 | O(N log2 N) | O(N log2 N) | No |
| 퀵 정렬 | O(N2) | O(N log2 N) | Yes |
Table. 1. 각종 정렬 알고리즘
⑵ 종류 1. 삽입 정렬(insertion sort)
① 개요
○ 가장 간단한 정렬 방식
○ 이미 순서화된 파일에 새로운 하나의 레코드를 순서에 맞게 삽입시켜 정렬
○ 두 번째 키와 첫 번째 키를 비교해 순서대로 나열(1회전)하고, 이어서 세 번째 키를 첫 번째, 두 번째 키와 비교해 순서대로 나열(2회전)하고, 계속해서 n번째 키를 앞의 (n-1)개의 키와 비교하여 알맞은 순서에 삽입하여 정렬하는 방식
Figure. 1. 삽입 정렬
② 알고리즘 (Python)
def insertion_sort(l):
n = len(l)
for i in range(2, n+1, 1):
# i = 2, 3, ..., n
# sorted: l[0], ..., l[i-2]
# unsorted: l[i-1], ..., l[n-1]
target = l[i-1]
flag = -1
for j in range(i-2, -1, -1):
# j = i-2, ..., 0
if(target < l[j]):
l[j+1] = l[j]
else:
l[j+1] = target
flag = 1
break
if(flag == -1):
l[0] = target
return l
insertion_sort([3, 2, 7, 6, 5, 9, 8])
# [2, 3, 5, 6, 7, 8, 9]
○ 전략 : 0부터 i-2번째 원소가 정렬돼 있고 i-1번째의 원소를 삽입하는 상황을 상정함
○ i-1번째의 원소를 삽입하기 위해 i-2번째 원소만 체크할 수도 있고 0부터 i-2번째 원소 모두를 체크해야 할 수도 있음
③ 시간복잡도
○ best case : i-2번째 원소만 체크하는 [1, 2, 3, ···]과 같은 경우
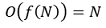
○ worst case : 0부터 i-2번째 원소를 모두 체크해야 하는 [9, 8, 7, ...]과 같은 경우
○ 시간복잡도 : 전체에 대한 Ο notation은 worst case를 기준으로 하므로,
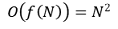
⑶ 종류 2. 버블 정렬(bubble sort)
① 개요
○ 주어진 파일에서 인접한 두 개의 레코드 키 값을 비교하여 그 크기에 따라 레코드 위치를 서로 교환하는 정렬 방식
○ 계속 정렬 여부를 플래그 비트(f)로 결정
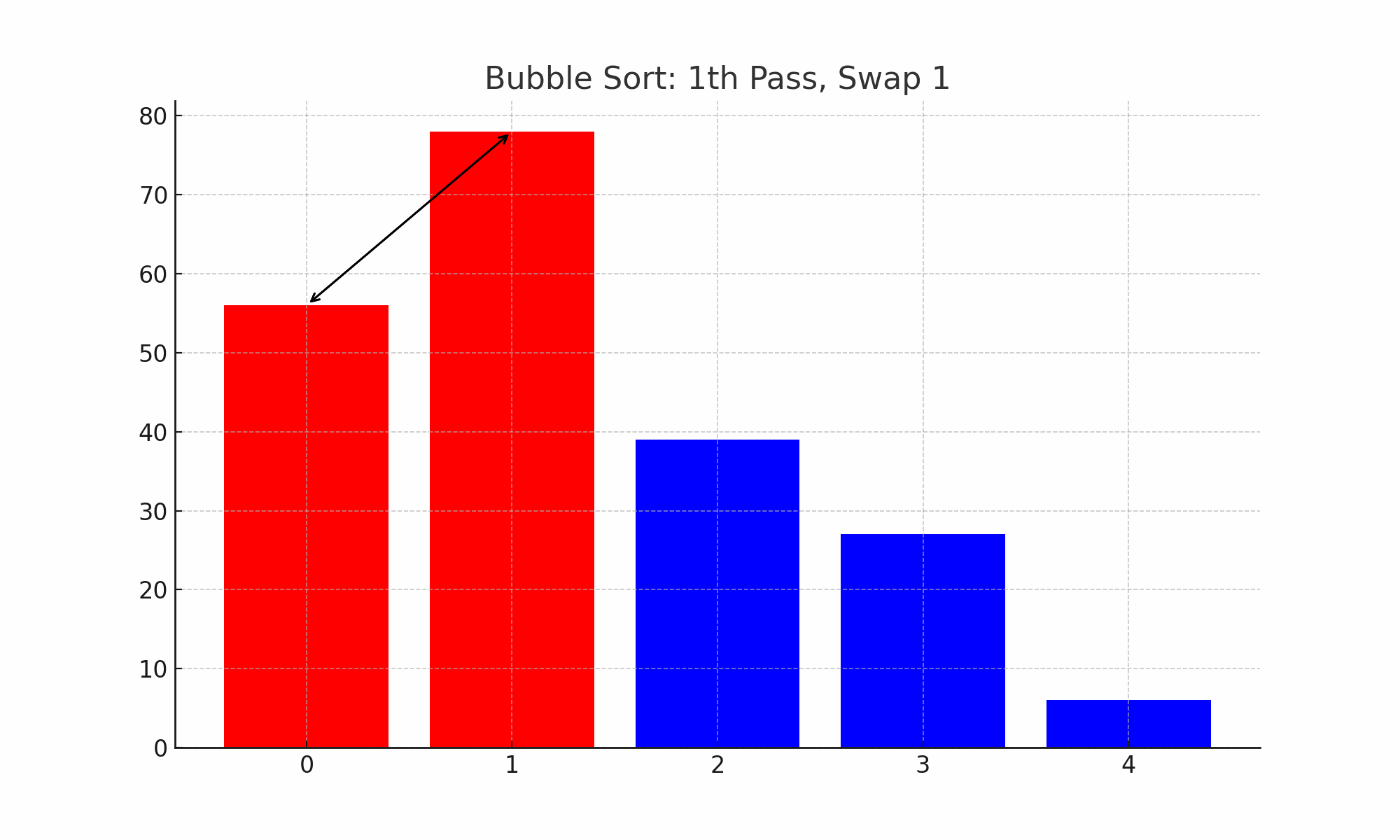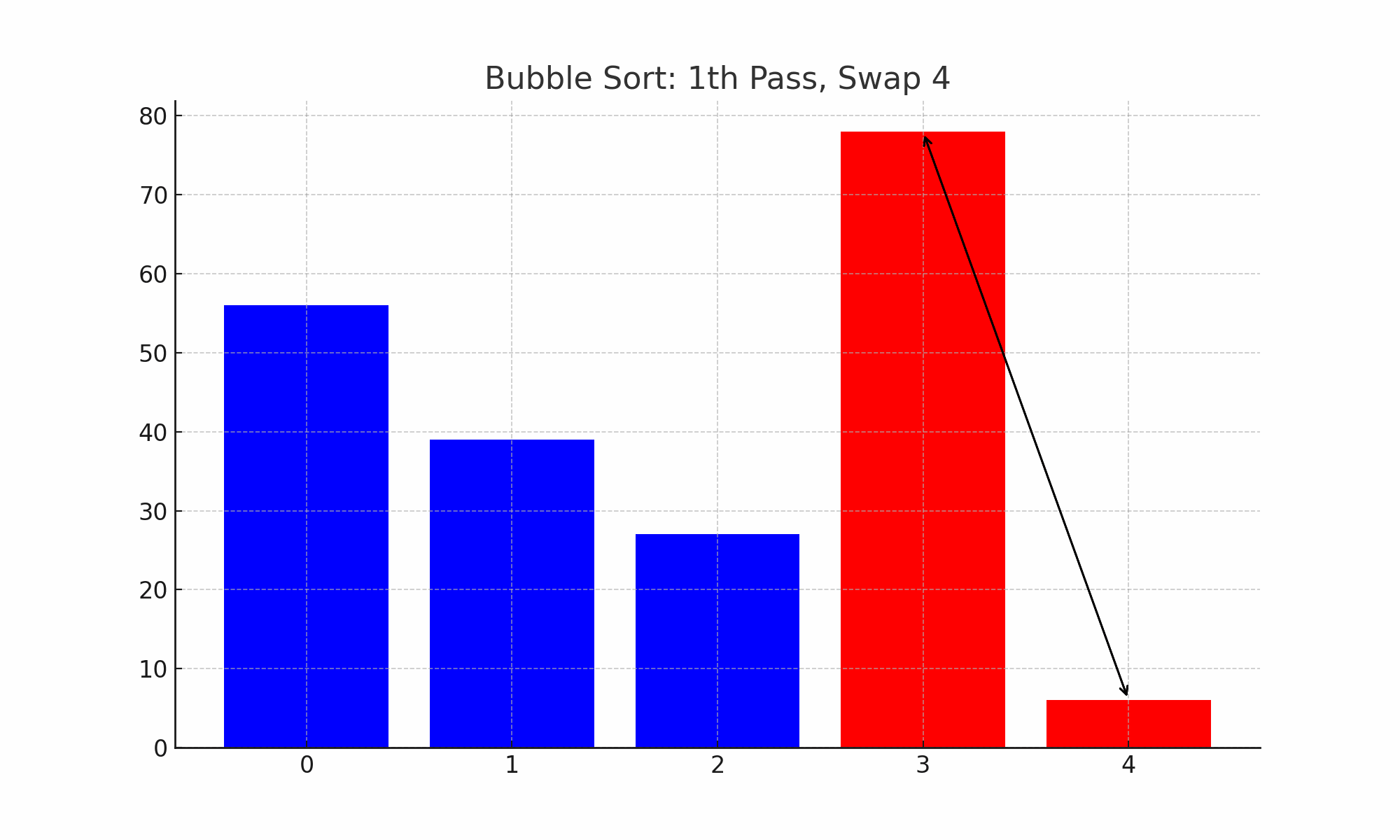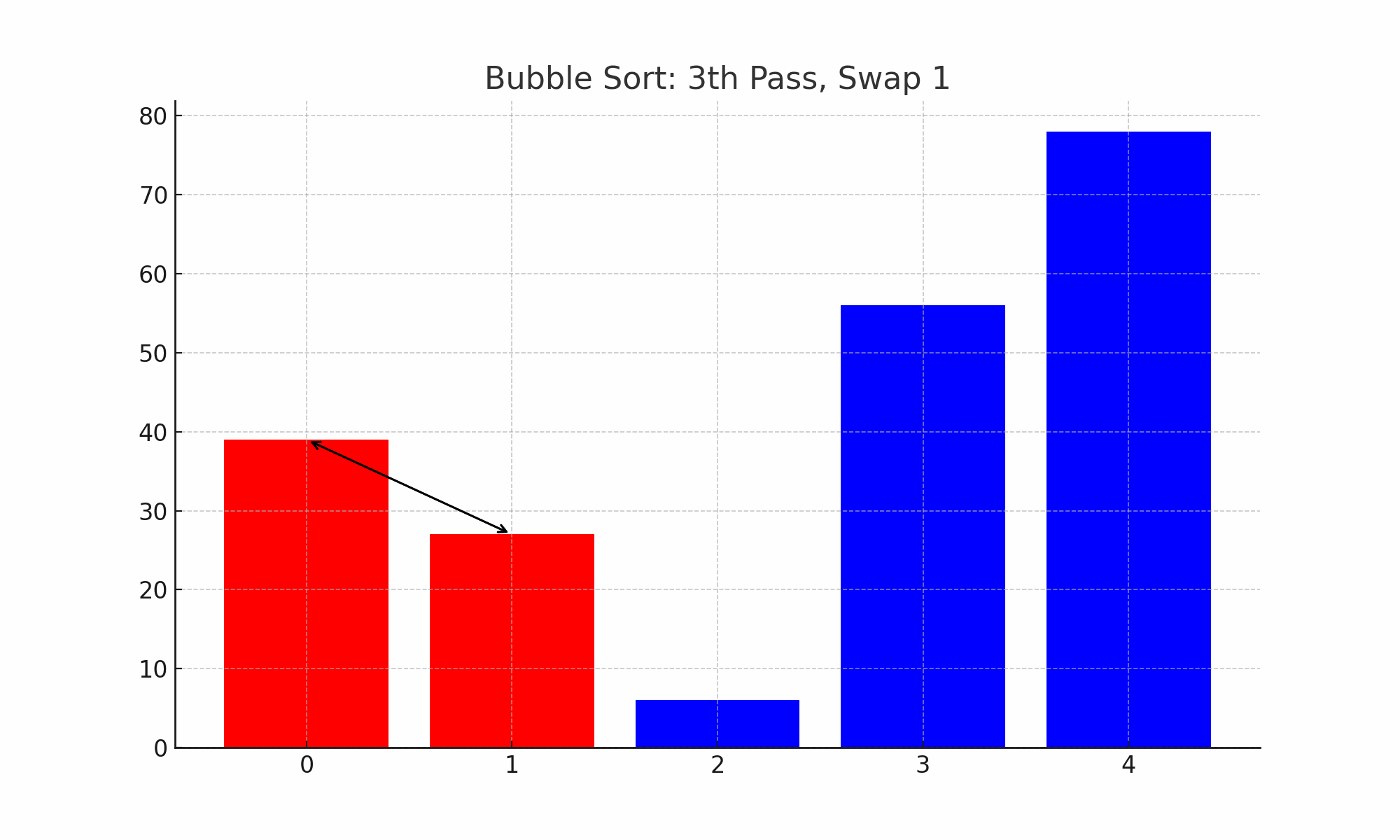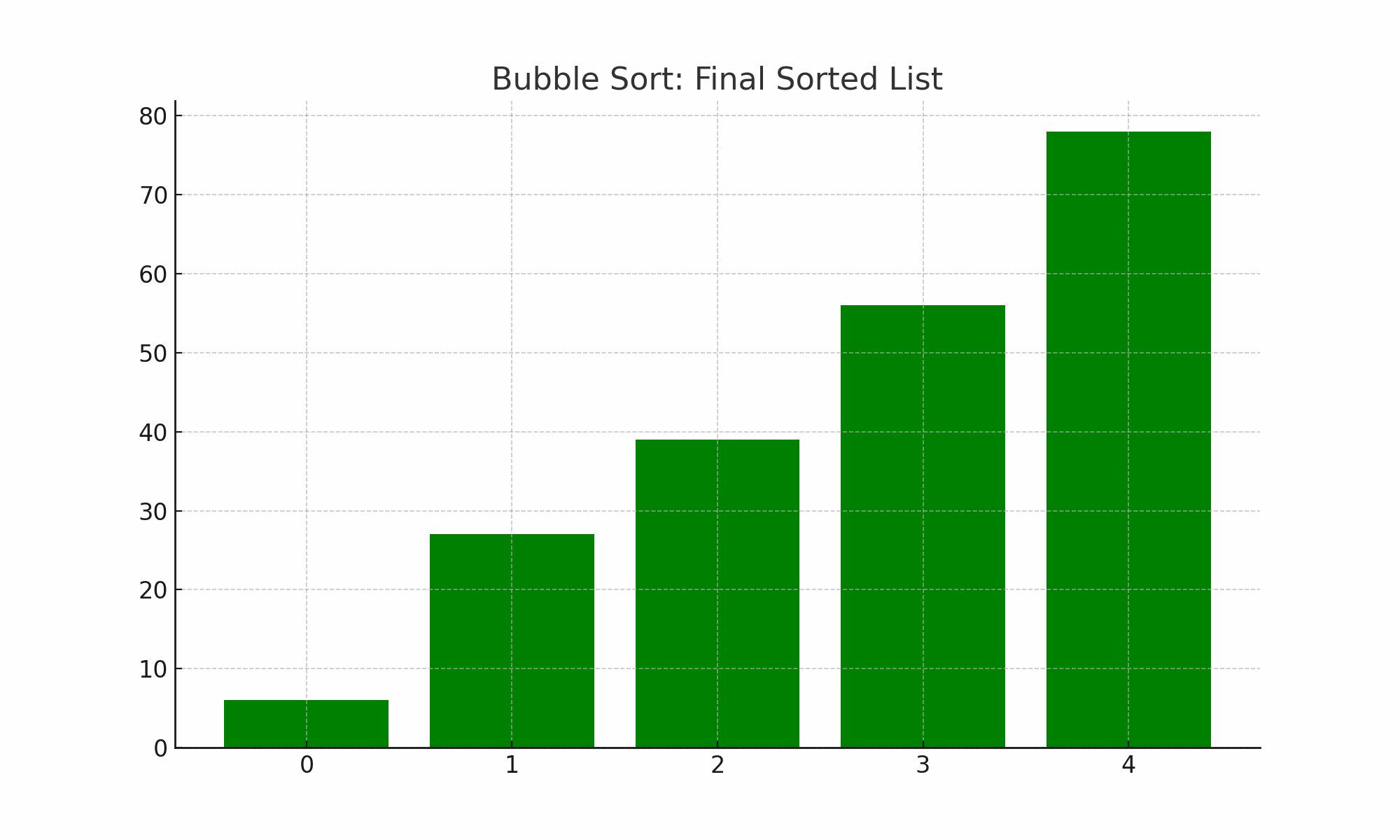
Figure. 2. 버블 정렬
② 알고리즘 (Python)
def bubble_sort(l):
def swap(i, j):
t = l[i]
l[i] = l[j]
l[j] = t
return
n = len(l)
for i in range(n, 1, -1):
# i = n, n-1, ..., 2
for j in range(0, i-1, 1):
# j = 0, ..., i-2
if(l[j] >= l[j+1]):
swap(j, j+1)
return l
bubble_sort([56, 78, 39, 27, 6])
# [6, 27, 39, 56, 78]
○ 전략 : 배열 앞에서 뒤로 훑을 때 swap을 하면 가장 큰 원소가 맨 뒤로 가게 됨
○ 함수 안에서만 작동하는 swap 함수를 따로 정의하여 코드의 간결성을 높임
③ 시간복잡도
○ best case : swap이 최소로 일어나는 [1, 2, 3, ···]과 같은 경우
○ worst case : swap이 최대로 일어나는 [9, 8, 7, ···]과 같은 경우
○ 시간복잡도는 best case, worst case를 불문하고 동일
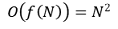
⑷ 종류 3. 선택 정렬(selection sort)
① 개요
○ 정의 : n개의 레코드 중에서 최소값을 찾아 첫 번째 레코드 위치에 놓고, 나머지 (n-1)개 중에서 다시 최소값을 찾아 두 번째 레코드 위치에 놓는 방식
○ 버블 정렬에 비해 swap의 수가 상당히 감소함
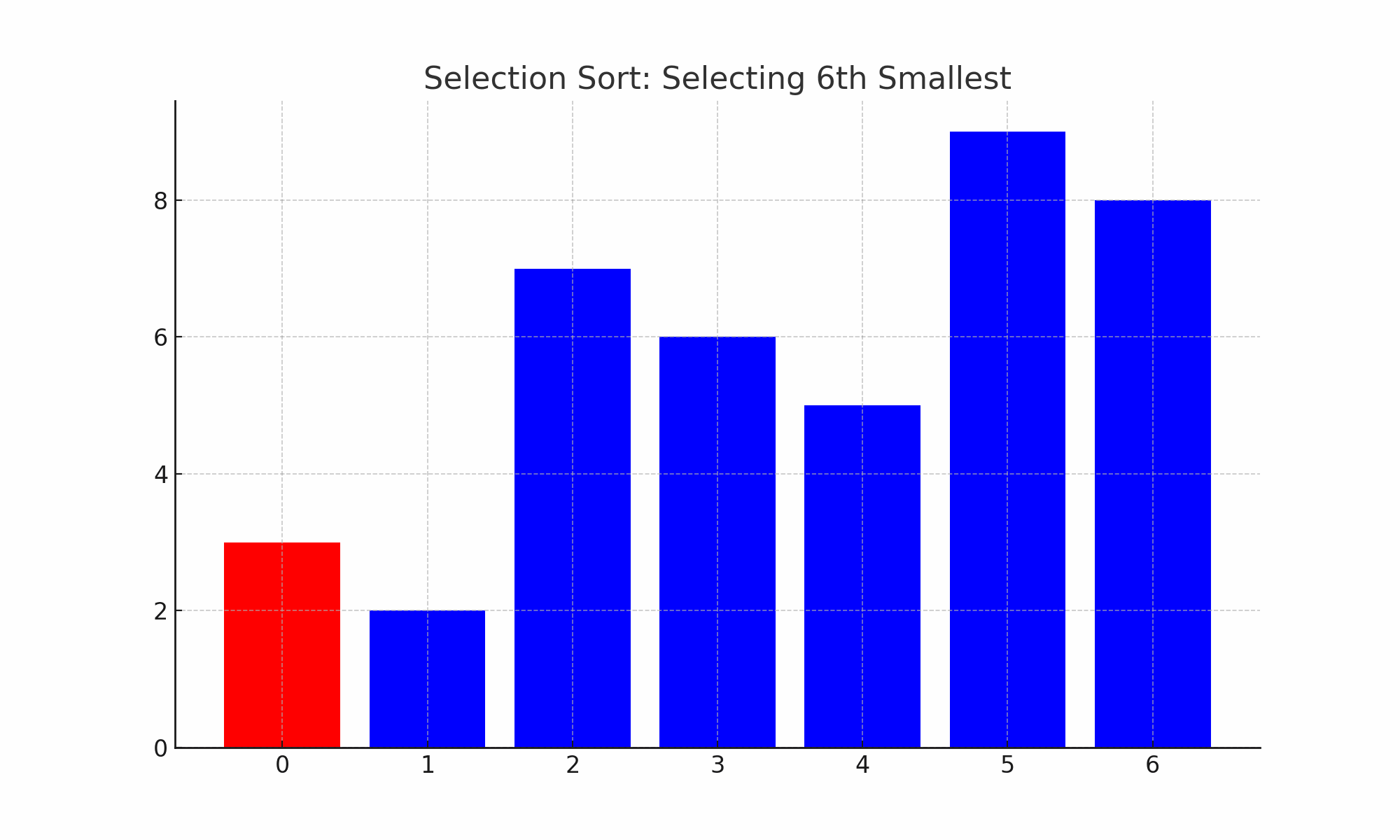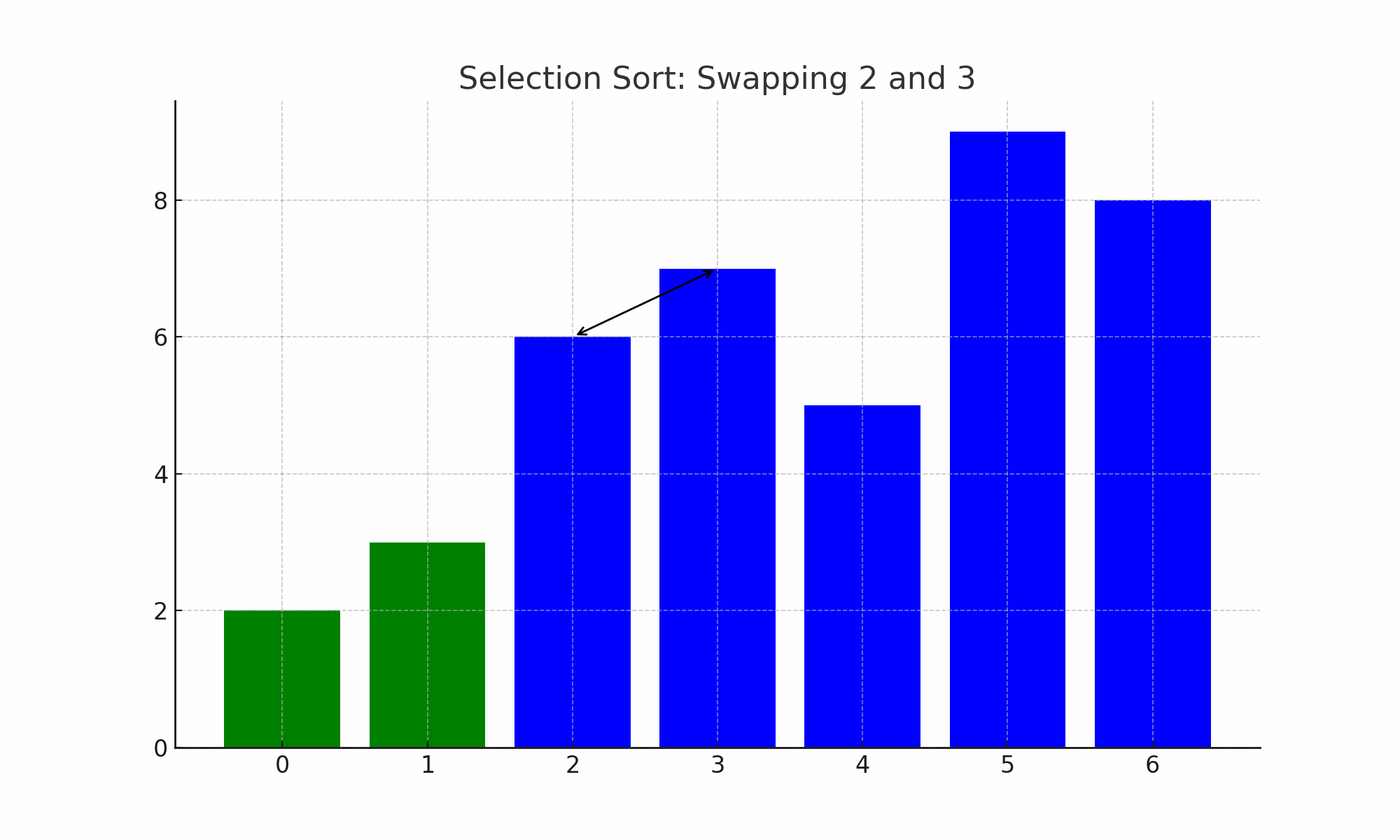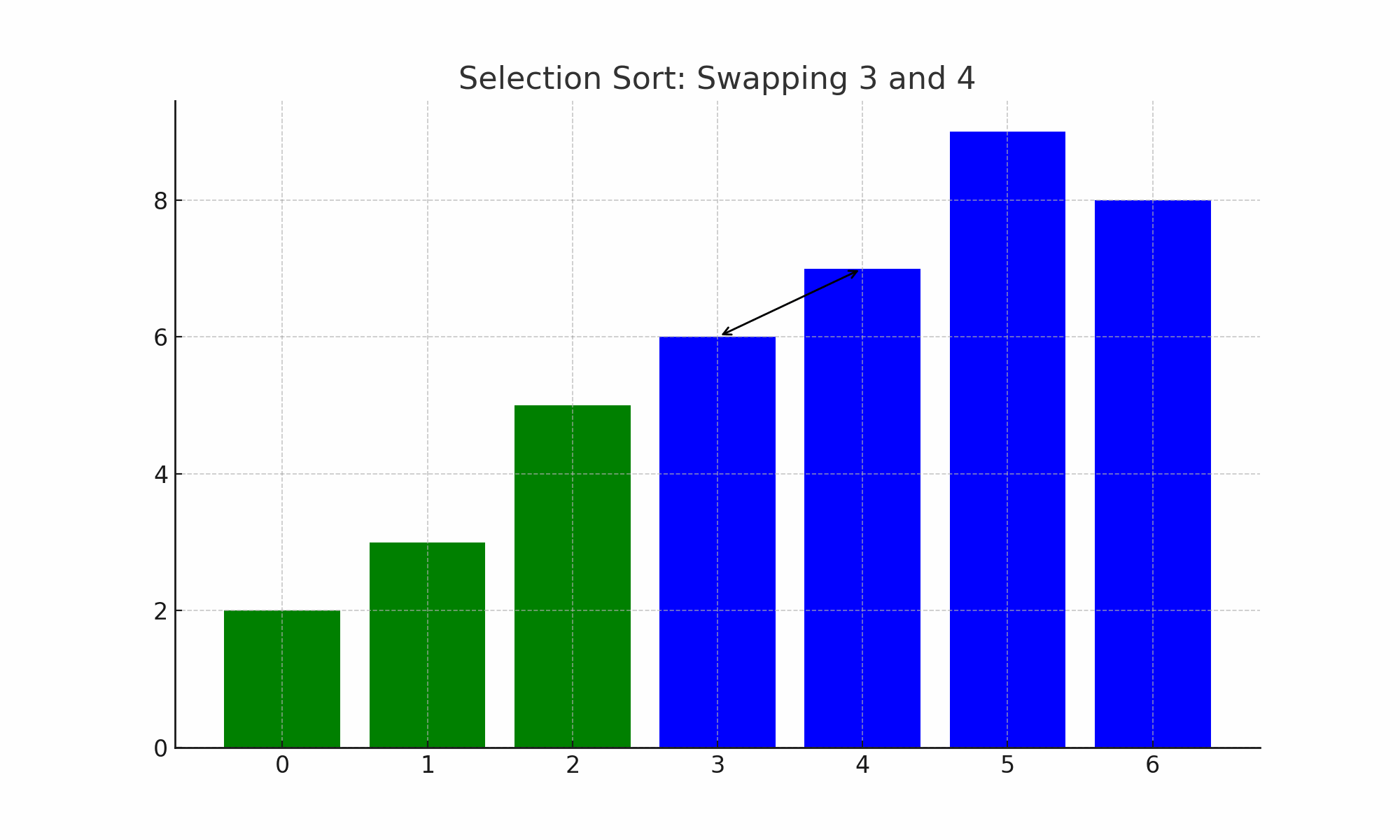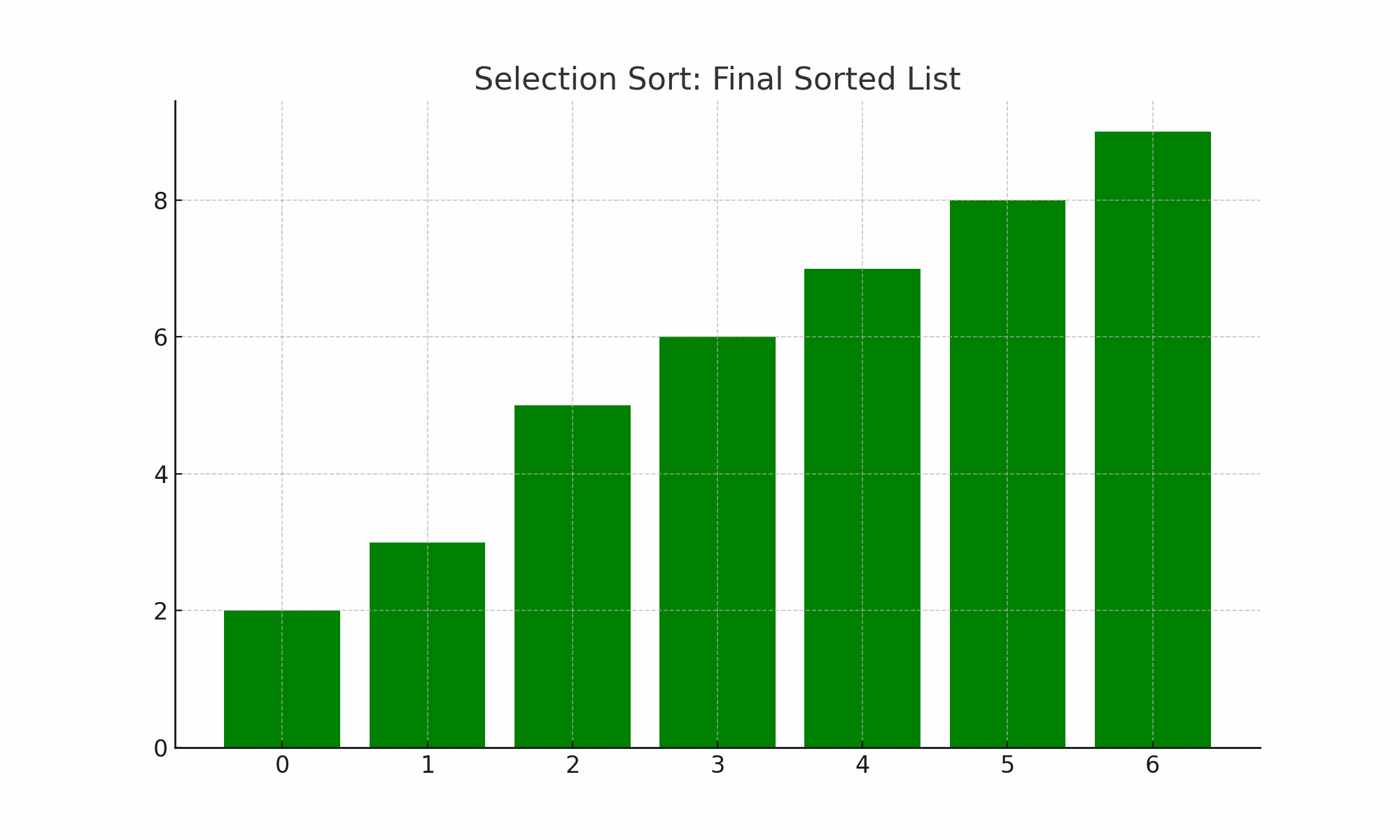
Figure. 3. 선택 정렬
② 알고리즘 (Python)
def selection_sort(l):
def swap(i, j):
t = l[i]
l[i] = l[j]
l[j] = t
n = len(l)
final_sorted_index = -1
for i in range(n-1, 0, -1):
# i = n-1, n-2, ..., 1
# final_sorted_index = -1, 0, ..., n-3
local_minimum = l[final_sorted_index + 1]
for j in range(final_sorted_index + 2, n, 1):
# sorted array: 0, ..., final_sorted_index
# j = final_sorted_index + 2, ..., n-1
if(l[j] < local_minimum):
local_minimum = l[j]
swap(final_sorted_index + 1, j)
final_sorted_index += 1
return l
selection_sort([3, 2, 7, 6, 5, 9, 8])
# [2, 3, 5, 6, 7, 8, 9]
○ 전략 : final_sorted_index까지는 정렬돼 있고 그 이후부터 n-1번째 중 최소 레코드를 찾아 sorted array에 넣음
③ 시간복잡도
○ best case : swap이 0번 일어나는 [1, 2, 3, ···]과 같은 경우
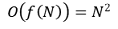
○ worst case : swap이 최대로 일어나는 [9, 8, 7, 6, ···]과 같은 경우
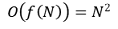
○ 시간복잡도 : best case, worst case를 불문하고 동일
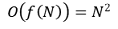
○ swap은 간단한 연산이기 때문에 선택정렬에서 best case, worst case를 굳이 구분하지 않기도 함
⑸ 종류 4. 병합 정렬(merge sort)
① 개요
○ 분할-정복 알고리즘(divide-and-conquer algorithm)의 한 종류
○ 분할 단계 : 주어진 배열을 절반으로 분할. 최소 시간이 소요되고 재귀적으로 수행
○ 정복 단계 : 두 개의 정렬된 배열을 합치는 단계
○ in-place 알고리즘이 아님 : 별도의 데이터 저장소를 요구함
② 알고리즘 (Python)
○ 병합 알고리즘
def merge(left, right):
len_left, len_right = len(left), len(right)
i_left, i_right = 0, 0
l = []
while((i_left < len_left) and (i_right < len_right)):
if(left[i_left] < right[i_right]):
l.append(left[i_left])
i_left += 1
else:
l.append(right[i_right])
i_right += 1
while(i_left < len_left):
l.append(left[i_left])
i_left += 1
while(i_right < len_right):
l.append(right[i_right])
i_right += 1
return l
○ 첫 번째 while 문 : left와 right 어느 쪽도 확인해 볼 필요가 있는 경우
○ 두 번째 while 문 : right는 더 이상 볼 필요가 없고 left만 보면 되는 경우
○ 세 번째 while 문 : left는 더 이상 볼 필요가 없고 right만 보면 되는 경우
○ 병합 정렬 알고리즘 : 재귀적으로 정의
def merge_sort(l):
if((len(l) == 0) or (len(l) == 1)):
return l
mid = int(len(l) / 2)
left = merge_sort(l[0:mid])
right = merge_sort(l[mid:])
r = merge(left, right)
return r
merge_sort([3, 2, 7, 6, 5, 9, 8])
# [2, 3, 5, 6, 7, 8, 9]
③ 시간복잡도
○ 소요 시간 계산
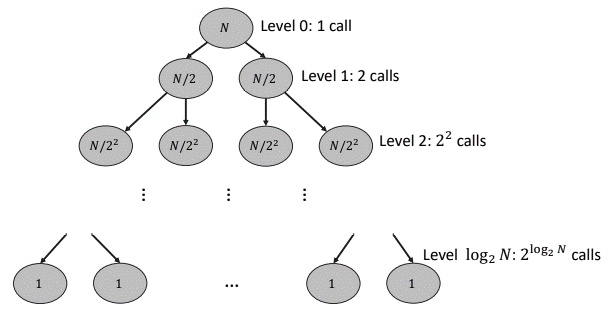
Figure. 4. 병합 정렬의 소요 시간 계산
○ merge() 함수는 O(N)임을 유의
○ Level 0 : merge()를 한 번도 호출하지 않으므로 O(1)
○ Level 1 : merge()를 1번 호출하므로 1 × O(N/2) = O(N/2) = O(N)
○ Level 2 : merge()를 2번 호출하므로 2 × O(N/4) = O(N/2) = O(N)
○ 총 소요시간 : O(N) + ··· + O(N) = O(N) × log2N = O(N log N)
○ best case : 첫 번째 while 문을 가장 빨리 통과할 수 있는 [1, 2, 3, ···]이나 [9, 8, 7, ···]과 같은 경우
○ worst cast : merge sort worst case generation code for Python (ref)
○ 발상 1. 짝수랑 홀수를 분리하는 식으로 하는 느낌
○ 발상 2. f([0, 1, 2, 3, 4, 5, 6, 7]) = (f[0, 2, 4, 6], f[1, 3, 5, 7])
○ 발상 3. f([0, 2, 4, 6]) = (f([0, 4]), f([2, 6]))
def merge(arr, left, right):
for i in range(0, len(left), 1):
arr[i]=left[i]
for i in range(0, len(right), 1):
arr[i + len(left)] = right[i]
def seperate(arr):
if(len(arr) <= 1):
return
if(len(arr) == 2):
swap=arr[0]
arr[0]=arr[1]
arr[1]=swap
return
m = int((len(arr) + 1) / 2)
left = [0] * m
right = [0] * (len(arr) - m)
i = 0
j = 0
while(True):
if(i >= len(arr)):
break
left[j] = arr[i]
i += 2
j += 1
i = 1
j = 0
while(True):
if(i >= len(arr)):
break
right[j] = arr[i]
i += 2
j += 1
seperate(left);
seperate(right);
merge(arr, left, right);
arr1= [0,1,2,3,4,5,6,7]
seperate(arr1);
print("For array 1:")
print(arr1);
# [4, 0, 6, 2, 5, 1, 7, 3]
arr2=[0,1,2,3,4,5,6,7,8]
seperate(arr2);
print("For array 2:");
print(arr2);
# [8, 0, 4, 6, 2, 5, 1, 7, 3]
○ 시간복잡도
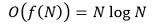
○ 시간 복잡도에서의 이익은 최대가 되지만 in-place 알고리즘이 아니라서 데이터 저장 용량 측면에서 상당히 불리함
⑹ 종류 5. 퀵 정렬(quick sort)
① 개요
○ 분할-정복 알고리즘(divide-and-conquer algorithm)의 한 종류
○ 분할 단계 : pivot (p)를 기준으로 작은 값은 왼쪽 서브파일에, 큰 값은 오른쪽 서브파일에 분할
○ 병합 단계 : 하나의 파일 내에 부분적으로 나뉜 두 서브파일을 병합
Figure. 5. 퀵 정렬 알고리즘의 과정
○ in-place 알고리즘 : 레코드의 많은 자료 이동을 없애고 별도의 저장 용량을 요하지 않아 병합 정렬과 다름
○ 튜링상을 받을 정도로 상당히 획기적인 알고리즘
○ 정렬 방식 중에서 가장 빠른 정렬 방법 중 하나로 프로그램에서 되부름을 이용하기 때문에 스택(Stack)이 필요함
② 알고리즘
○ non-in-place 분할 알고리즘 (Python) : small, large라는 별도의 storage가 필요함
def partition(l, low, high):
p = l[low]
small = []
large = []
for i in l[low+1:high+1]:
if(i < p):
small.append(i)
else:
large.append(i)
small.append(p)
idx = low
for i in small:
l[idx] = i
idx += 1
for i in large:
l[idx] = i
idx += 1
return (low + len(small) - 1)
○ in-palce 분할 알고리즘 (Python) : 튜링상을 받은 이유 1
def partition(l, low, high):
def swap(i, j):
t = l[i]
l[i] = l[j]
l[j] = t
return
p = l[low]
m = low
for j in range(low + 1, high + 1):
if(l[j] < p):
m += 1
swap(j, m)
swap(low, m)
return m
○ m : pivot보다 작은 원소의 개수
○ 퀵 정렬 알고리즘 (Python)
def quick_sort(l):
def qs(l, low, high):
if(low < high):
pivot_idx = partition(l, low, high)
qs(l, low, pivot_idx - 1)
qs(l, pivot_idx+1, high)
return l
qs(l, 0, len(l) - 1)
return l
③ 시간복잡도
○ 퀵 정렬은 Ο notation의 시간복잡도가 최적화된 편 (ref)
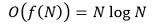
○ 대개 빅 데이터를 다룸을 감안하면 퀵 정렬과 같은 알고리즘을 사용하는 것이 훨씬 전략적
○ 다만, cache와의 적합성 등을 고려하면 데이터베이스마다 달라질 수 있음
○ 위 시간복잡도는 현실적인 시간복잡도이지 worst case의 시간복잡도를 얘기하는 게 아님
○ best cast : 나누어지는 족족 반씩 분할되는 경우
○ 문제의 정의
○ quick sort best case generation code for Python (ref; 단, 여기 링크에서 코드는 오류가 있었음)
○ 발상 1. f([1, 2, 3, 4, 5, 6, 7, 8, 9]) = (5, f(1, 2, 3, 4), f(6, 7, 8, 9))
○ 발상 2. f([1, 2, 3, 4]) = (3, f([1, 2]), f([4]))
def generate(arr, begin, end):
# begin : inclusive
# end : exclusive
if(end - begin <= 1):
return
middle = int((begin + end)/2)
generate(arr, begin, middle)
generate(arr, middle+1, end)
temp = arr[middle]
for i in range(middle-1, begin-1, -1):
arr[i+1] = arr[i]
arr[begin] = temp
def fillArray(arr):
for i in range(0, len(arr), 1):
arr[i] = i+1
intCount = 15
arr = [0] * intCount
fillArray(arr)
generate(arr, 0, len(arr))
print(arr)
# [8, 4, 2, 1, 3, 6, 5, 7, 12, 10, 9, 11, 14, 13, 15]
○ 횟수의 계산
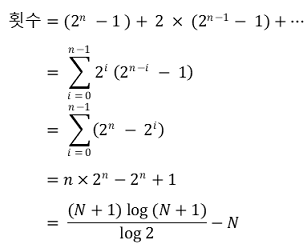
○ 시간복잡도
○ worst cast : 나누어지는 족족 1개와 나머지로 분할되는 [1, 2, 3, ···]과 같은 경우
○ 문제의 정의
○ 횟수의 계산
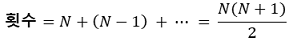
○ 시간복잡도
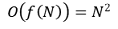
○ worst case를 실행시킬 때 memory limit을 초과하거나 재귀함수 호출 횟수 제한을 초과할 수 있음을 유의
○ average case (improved)
○ worst case는 divide의 이익을 제대로 이용하지 못함
○ average case는 divide의 이익을 절반 정도는 이용할 것이므로 best case와 유사해짐
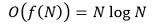
○ 이 점 때문에 퀵 정렬이 Ο(N log N)으로 알려져 있음
○ average case에 대해서 merge sort보다 더 빠름 : 튜링상을 받은 이유 2
○ 시간복잡도 : 전체에 대한 Ο notation은 worst case를 기준으로 하지만, 이 경우에는 average case를 강조하여
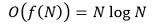
3. non-comparison-based 정렬 알고리즘 [목차]
⑴ 개요
① 일반적으로 객체 자체를 비교하기보다 객체가 가진 키(key)를 중심으로 비교함
② stable algorithm : 같은 키 값을 가지는 레코드의 상대적인 순서를 보존해 주는 알고리즘
○ 버블 정렬, 삽입 정렬, 선택 정렬, 병합 정렬, 카운팅 정렬은 stable algorithm
○ 퀵 정렬은 stable algorithm이 아님
③ (주석) 단순히 숫자만 있는 경우 comparison-based 정렬 알고리즘을 쓰는 건 비효율적
⑵ 종류 1. 카운팅 정렬(counting sort)
① 정의 : 각 키 값이 개성이 없는 경우 단순히 키 값의 카운팅을 활용하면 시간복잡도를 효과적으로 줄일 수 있음
② stable algorithm이라는 게 중요한 특징
③ 알고리즘 (Python)
def counting_sort(l, m):
# l : the given array
# m : the types of numbers
c = [0] * (m + 1)
# c = [0, 0, 0, 0]
for i in l:
c[i] += 1
for j in range(1, m+1):
c[j] = c[j-1] + c[j]
n = len(l)
t = [0] * n
for i in range(n-1, -1, -1):
# i = n-1, ..., 0
j = l[i]
t[c[j] - 1] = j
c[j] = c[j] - 1
for i in range(0, n):
l[i] = t[i]
return l
l = [2, 1, 3, 2, 3]
counting_sort(l, 3)
# [1, 2, 2, 3, 3]
○ c[i] += 1 : 키 값이 i 값인 경우가 몇 개 있는지를 나타냄
○ c[j] = c[j-1] + c[j] : 특정 j 값을 가지는 키가 최대 몇 번째에 위치하는지를 나타냄
○ t[c[j] - 1] = j : c[j]는 몇 번째이므로 배열 index로 나타내려면 1을 빼주어야 함
○ c[j] = c[j] - 1 : 이미 특정 j 값을 가진 키를 접한 경우를 고려하여 그 j 값을 가지는 최대 위치를 줄여야 함
○ stable algorithm인 이유 : i = n-1, ..., 0으로 뒤에서 접근하는데 특정 키 값의 최대 위치를 고려했으므로
④ 시간복잡도
○ 알고리즘을 보면 best case, worst case 구분이 불명확함
○ 다만, c라는 배열의 크기에 따른 자료 입출력 속도가 중요할 것으로 여겨짐
○ best case : 배열 l에 오직 한 가지의 원소만 있는 경우
○ worst case : 배열 l에 어느 두 원소도 동일하지 않은 경우
○ 시간복잡도
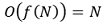
⑶ 종류 2. 쉘 정렬(shell sort)
① 입력 파일을 어떤 매개변수(h) 값으로 서브 파일을 구성하고, 각 서브파일을 삽입 정렬 방식으로 순서 배열하는 과정을 반복하는 정렬 방식 : 보통 h=n1/3
② 즉 임의의 레코드 키와 h 값만큼 떨어진 곳의 레코드 키를 비교하여 순서화되어 있지 않으면 서로 교환하는 것을 반복하는 정렬 방식
③ 삽입 정렬을 확장한 개념으로 입력 파일이 부분적으로 정렬되어 있는 경우 유리함
⑷ 종류 3. 기수 정렬(bucket sort) : radix sort라고도 함
① 자릿수별로 레코드 키 값을 분석하여 자릿수별로 그 순서에 맞는 버킷(큐)에 분배하였다가 버킷 순서대로 레코드를 꺼냄
② 즉, 자릿수별로 카운팅 정렬을 쓴 것
③ 알고리즘 (Python)
def radix_sort(l, d):
# d : maximum number of digits
for r in range(0, d):
# r : from 1's digit to 100's digit
c = [0] * 10 # 0, 1, ..., 9
m = d - r - 1 # m : the specific digit
for i in l:
key = int(str(i)[m])
c[key] += 1
for j in range(1, 10):
c[j] = c[j-1] + c[j]
n = len(l)
t = [0] * n
for i in range(n-1, -1, -1):
# i = n-1, ..., 0
key = int(str(l[i])[m])
t[c[key]-1] = l[i]
c[key] = c[key] - 1
for i in range(0, n):
l[i] = t[i]
return l
l = [232, 324, 333, 212, 128]
radix_sort(l, 3)
# [128, 212, 232, 324, 333]
④ 시간복잡도
○ best case : 모든 숫자가 동일한 경우
○ worst case : 각 자릿수의 종류가 최대한 다양한 경우
○ 시간복잡도 : 자릿수별로 카운팅 정렬을 쓴 것이므로,
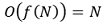
⑸ 종류 4. 힙 정렬(heap sort)
① 전이진 트리(complete binary tree)를 이용한 정렬 방식
4. AI-based 정렬 알고리즘 [목차]
⑴ 2023년 6월 딥마인드에서 나온 논문에 따르면 AI를 통해 정렬 알고리즘을 작성할 수 있음이 밝혀짐 (ref)
⑵ 딥러닝에도 많이 사용되는 정렬 알고리즘이 비효율적인 고전적 정렬 알고리즘에 의존한 게 아이러니 했다는 말이 나오는 상황
입력 : 2016.08.30 21:49
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 3강. 자료구조 (0) | 2021.09.22 |
|---|---|
| 【알고리즘】 2강. 탐색 알고리즘 (0) | 2021.09.22 |
| 【알고리즘】 2-1강. 탐색 알고리즘 실험 (0) | 2020.07.05 |
| 【알고리즘】 23-1강. 뉴턴-랩슨법(Newton-Raphson method) (0) | 2019.11.12 |
| 【알고리즘】 6-1강. Calibrated Classification Model (0) | 2019.11.08 |
최근댓글