2강. 탐색 알고리즘(search algorithm)
추천글 : 【알고리즘】 알고리즘 목차
a. 탐색 알고리즘 실험
1. 개요 [목차]
⑴ 탐색(search)
① 배열 C ={a1, a2, ···, an}이 있고 키 e가 있을 때 ai = e인 ai를 찾는 과정
② 위 조건을 만족하는 가장 최초의 원소
③ 또는, 위 조건을 만족하는 가장 최후의 원소
④ 또는, 위 조건을 만족하는 모든 원소
⑵ 배열 C가 정렬된 배열일 수도 있고, 정렬되지 않은 배열일 수도 있음
① 선형탐색 : O(N)
② 이진탐색 : O(log2 N)
③ 정렬 후 1번 탐색 : O(N log2 N) + O(log2 N) = O(N log2 N)
④ 정렬 후 N번 탐색 : O(N log2 N) + N × O(log2 N) = O(N log2 N)
⑤ 정렬된 배열을 N번 탐색 : N × O(log2 N) = O(N log2 N)
⑶ 종류
① 종류 1. 깊이 우선 탐색(DFS, depth-first search)
○ 스택(stack) 기반
○ 메모리 사용 : O(D) 또는 O(D × B) (단, O는 max depth, B는 branching factor)
○ 가장 짧은 경로를 언제나 찾을 수 있는 것은 아님
depth_first(value):
do_I_match_value?
depth_first(children)
② 종류 2. 너비 우선 탐색(BFS, breadth-first search)
○ 큐(queue) 기반
○ 메모리 사용 : O(BD) (단, O는 max depth, B는 branching factor)
○ 가장 짧은 경로를 언제나 찾을 수 있음
breadth_first(value):
queue = [root node]
for each item in queue:
do_I_match_value?
append all children to queue
2. 선형탐색(linear search) [목차]
⑴ 개요
① 각 원소를 차례대로 훑으면서 특정 원소가 있는지 확인하는 방법
② 정렬된 배열이어도 되고 정렬되지 않은 배열이어도 됨
③ 시간복잡도
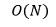
⑵ 알고리즘 (Python)
① 탐색 여부를 반환하는 선형 탐색 알고리즘
def linear_search (l, e):
found = False
for i in l:
if(i == e):
found = True
return found
② 탐색된 원소의 순서를 반환하는 선형 탐색 알고리즘
def linear_search_idx (l, e):
n = len(l)
idx = -1
for i in range(n):
if(l[i] == e):
idx = i
return idx
③ 정렬된 배열에 대한 선형 탐색 알고리즘
def linear_search_sorted (l, e):
found = False
for i in l:
if(l[i] == e):
found = True
break
if(i > e):
found = False
break
return found
3. 이진탐색(binary search) : 이진트리탐색(binary tree search)이라고도 함 [목차]
⑴ 개요
① 이진 탐색은 반드시 정렬된 알고리즘을 전제로 함
⑵ 이진 트리(binary tree)
① 정의 : 차수(degree)가 2 이하인 노드들로 구성된 트리, 즉 자식이 둘 이하인 노드들로만 구성된 트리
② 이진 트리의 레벨 i에서 최대 노들의 수는 2i-1
③ 종류 1. 정이진 트리(Full Binary Tree) : 꽉 차 있는 트리
④ 종류 2. 전이진 트리(Complete Binary Tree) : 맨 마지막 잎만 차 있지 않은 경우
⑤ 종류 3. 사향 이진 트리(Skewed Binary Tree) : 왼쪽 혹은 오른쪽으로만 자식이 있는 특별한 이진트리
⑶ 탐색의 원리
4, 6, 5, 3, 7, 2와 같은 수열이 주어져 있을 때 이진트리는 다음과 같이 구성해 보자.
우선 4가 root에 붙고, 그 뒤 온 6이 4보다 크므로 4의 오른쪽으로 붙는다. 또 5는 4보다 크므로 6의 방향으로 가는데, 6보다 크기가 작으므로 6의 왼쪽에 붙는다. 이런 식으로 트리가 구성된다. 각 node의 명칭부터 살펴보면 직접적으로 연결돼 있는 두 node 중 root와 가까운 쪽을 parent node, root에서 먼 쪽을 sibling node라고 부른다. 또, sibling node는 앞서 트리를 구성하는 과정에서도 보았듯 left sibling node와 right sibling node가 있다. 더 나아가 한 node에서 다른 node로 쭉 내려가는 경로가 있다면, 전자를 ancestor node, 후자를 descendant node라고 부른다.
이진트리 내 각 node를 이진법으로 나타내면 여러 연산을 처리하기 용이하다. 이때 각 대체수는 다음과 같이 정의된다.
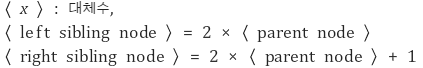
그러면 4는 1, 3은 10, 6은 11, 5는 110이 된다.
주어진 이진트리 내에서 특정 값이 있는지를 찾아보는 과정을 이진트리탐색 혹은 이진트리순회라고 한다. 이진트리탐색은 총 4가지 방법이 있다. 첫째, in-order traversal은 왼쪽, 가운데, 오른쪽 순으로 탐색하는 방법으로, 2-3-4-5-6-7로 순회할 수 있다. 탐색하는 node의 순서를 출력하면, 트리 내 node의 값을 크기순서로 출력하는 결과를 얻는다. 둘째, level-order traversal는 각 node의 level(root로부터의 최단거리)가 작은 순서대로 node를 탐색하는 방법이다. 4-3-6-2-5-7로 순회할 수 있다. 셋째, pre-order traversal은 가운데, 왼쪽, 오른쪽 순으로 탐색하는 방법으로으로 4-3-2-6-5-7로 순회할 수 있다. 마지막으로 post-order traversal은 왼쪽, 오른쪽, 가운데 순으로 탐색하는 방법으로 2-3-5-7-6-4로 순회할 수 있다. 이진트리탐색을 알고리즘으로 구현할 시 재귀 함수로 하는 게 일반적이다. 가령 in-order traversal을 구현할 시 f(4) = f(3) + 4 + f(6)과 같이 하는 식이다. 즉,
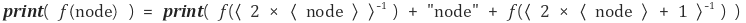
이제 level-ancestor(LA) 연산에 대해 소개하겠다. LA(x, k)는 x의 값을 가지는 node의 ancestor node 중 level이 k인 node의 값이 얼마인지를 나타낸다. 예를 들어, LA(2, 1) = 3이고, LA(5, 3) = -1이다. 이때, -1은 예외의 상황을 위한 값으로 그 예시처럼 주어진 node보다 높은 level을 말하면 항상 -1이 된다. 이 연산도 대체수를 이용하면 쉽게 계산된다.

이때 log 값은 x의 대체수의 자릿수 - 1이다. 이 값은 쉽게 구할 수 있다.
또다른 연산은 lowest-common-ancestor(LCA)이다. LCA(x, y)는 x 값을 가지는 node와 y 값을 가지는 node의 공통 ancestor node 중에서 가장 가까운(= 가장 level이 큰) node의 값이 얼마냐 하는 것이다. 예를 들어, LCA(5, 7) = 6, LCA(2, 6) = 4인 식이다. 이것도 대체수를 이용해서 계산할 수 있다.

이밖에도 여러 연산들이 있으며, 이 또한 대체수를 이용해서 계산된다. 이렇듯 창의적인 방법론이 문제를 얼마나 쉽게 바꿔 버리는지를 주목하길 바란다.
⑷ 알고리즘 (Python)
① 재귀함수를 이용한 알고리즘
def binary_search (l, e):
def bs(l, low, high, e):
if(low > high):
return -1
i = int((low+high)/2)
if(l[i] == e):
return i
elif (l[i] < e):
i = bs(l, i+1, high, e)
else:
i = bs(l, low, i-1, e)
return i
return bs(l, 0, len(l)-1, e)
② 반복을 이용한 알고리즘
def binary_search_iter (l, e):
low = 0
high = len(l) - 1
while(low < high):
i = int((high + low) / 2)
if(l[i] == e):
return i
elif(l[i] < e):
low = i + 1
else:
high = i-1
return -1;
4. 기타 탐색 알고리즘 [목차]
⑴ 종류 1. elastic search : 구글에서도 쓰는 자연어 서치 알고리즘
입력: 2016.09.18 21:47
'▶ 자연과학 > ▷ 알고리즘·머신러닝' 카테고리의 다른 글
| 【알고리즘】 1-1강. 정렬 알고리즘 실험 (0) | 2021.10.01 |
|---|---|
| 【알고리즘】 3강. 자료구조 (0) | 2021.09.22 |
| 【알고리즘】 1강. 정렬 알고리즘 (2) | 2021.09.14 |
| 【알고리즘】 2-1강. 탐색 알고리즘 실험 (0) | 2020.07.05 |
| 【알고리즘】 25-1강. 뉴턴-랩슨법(Newton-Raphson method, Newton method) (0) | 2019.11.12 |





최근댓글