17강. 비선형 회귀분석(non-linear regression model)
추천글 : 【통계학】 통계학 목차
a. R로 하는 회귀분석
1. 이차회귀모델(quadratic regression model) [목차]
⑴ 수식화
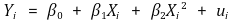
⑵ 계수 결정
① 다중선형회귀모델 이용 : Xi와 Xi2를 서로 다른 변수로 간주하고 해석
② Xi와 Xi2는 완전 다중공선성(perfect multi-collinearity)이 없으므로 가능
⑶ 선형성 테스트(linearity test)

⑷ 변화량의 신뢰구간
① 효과(effect) : X의 단위변화에 따른 Y의 효과는 다음과 같음
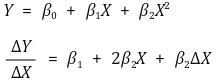
② marginal effect
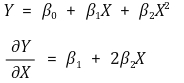
③ 변화량의 표준편차
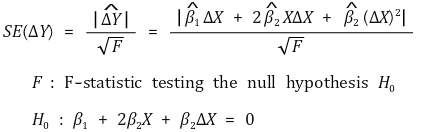
④ 변화량의 신뢰구간
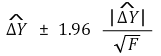
2. 다항회귀모델(polynomial regression model) [목차]
⑴ 일반식
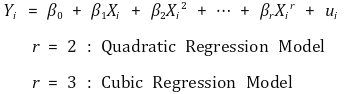
⑵ 계수 결정 : 다중선형회귀모델 이용
⑶ 선형성 테스트(linearity test)
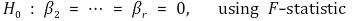
⑷ 차수 결정 방법 1. top-down 방식
① 가장 일반적으로 채택되는 방식
② 1st. 최대치 r을 설정
③ 2nd. H0 : βr = 0을 검정
④ 3rd. H0를 기각할 경우 r이 회귀선의 차수
⑤ 4th. H0를 기각하지 못하면 Xir을 제거하고 βr-1, ···에 대해서 2nd를 반복
⑸ 차수 결정 방법 2. bottom-top 방식
① 한 단계 차수가 높은 항을 추가했을 때 주어진 샘플을 설명하는 데 유의미한 효과가 있는지를 보는 방식
② 과정
○ 1st. r-1차 다항식까지 bottom-top 방식으로 모든 항의 계수가 유의미하다고 가정
○ 2nd. r차 항을 추가
○ 3rd. r차 회귀선에 의한 제곱합을 계산 (자유도 : r)
○ 4th. 3rd에서 계산한 값에 r-1차 회귀선에 의한 제곱합 (자유도 : r-1)을 뺌
○ 5th. r차 회귀선의 잔차에 의한 제곱합 (자유도 : n-1-r)을 계산
○ 6th. 5th에서 계산한 값을 n-1-r로 나누어 평균제곱을 계산
○ 7th. 4th에서 얻은 제곱합의 차를 6th에서 얻은 평균제곱으로 나눔 : 제곱합의 차의 자유도는 1
○ 8th. 7th에서 얻은 F 통계량을 F(1, n-1-r)에 대입하여 p value 계산
③ 예제
○ 문제 상황
| 모델 | 제곱합 | df | 평균제곱 |
| Linear | 3971.46 | 1 | 3971.46 |
| Error | 372515.09 | 18 | 20695.28 |
| Quadratic | 367833.58 | 2 | 183916.79 |
| Error | 8652.97 | 17 | 509.10 |
| Cubic | 369211.71 | 3 | 123070.57 |
| Error | 7274.84 | 16 | 454.68 |
(출처 : Statistics Explained 2nd edition-Steve McKillup-Cambridge-2012)
Table. 1. 문제 상황
○ 결과표
| 모델 | 제곱합의 차 | df | 잔차 제곱합 | df | 잔차 제곱합의 평균 | F 비 |
| Quadratic | 367833.58 | 2 | 8652.97 | 17 | 509.10 | F1,17 = 714.72 |
| Linear | 3971.46 | 1 | P < 0.001 | |||
| Difference | 363862.12 | 1 | ||||
| Cubic | 369211.71 | 3 | 7274.84 | 16 | 454.68 | F1,16 = 3.03 |
| Quadratic | 367833.58 | 2 | NS | |||
| Difference | 1378.13 | 1 |
Table. 2. 결과표
④ 단점 : sequential type Ⅰ error accumulation이 논란이 됨
○ 통계라는 학문은 한 번에 나타난 현상을 가지고 분석하는 것
○ 특정 확률을 갖고 나타난 현상에 대해 다시 거기서 다른 확률을 갖는 현상을 분석하는 굉장히 까다로움
○ 까다롭다는 의미는 F 분포를 따르지 않을 수도 있다는 의미
○ bottom-top 방식의 차수 결정 방법은 특정 확률의 현상에서 다른 확률의 현상을 분석하는 것
○ 특정 확률의 현상은 r-1차 회귀식을 지칭하는 것임
○ 다른 확률의 현상은 r차 회귀식을 지칭하는 것임
○ (주석) 분명하게 F 분포를 따름을 증명할 수 없는 듯
3. 로그회귀모델(logarithm regression model) [목차]
⑴ (참고) 로그 근사식
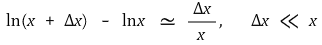
⑵ 종류 1. 선형-로그 모델(linear-log model)
① 수식화
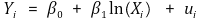
② Xi가 1% 증가하면 Yi는 0.01β1 만큼 증가
⑶ 종류 2. 로그-선형 모델(log-linear model)
① 수식화
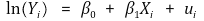
② Xi가 1만큼 증가하면 Yi는 100β1% 만큼 증가
⑷ 종류 3. 로그-로그 모델(log-log model)
① 수식화
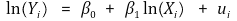
② Xi가 1% 증가하면 Yi는 β1% 만큼 증가
⑸ adjusted R2를 비교하여 로그-선형 모델과 로그-로그 모델 중 더 적합한 모델을 선택할 수 있음
⑹ 선형-로그 모델은 종속변수의 종류가 다르므로 다른 모델과 adjusted R2를 비교하는 것은 무의미
4. 확률 모델(probability model) : 종속변수가 이진변수(binary variable)인 경우 [목차]
⑴ 선형 확률 모델(LPM, linear probability model)
① 수식화
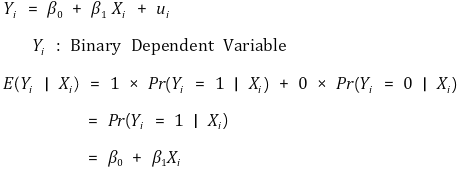
② 문제점 : 종속변수가 항상 0 ~ 1 사이의 값을 보여주지 않음
⑵ probit regression model
① 개요 : 확률 모델로서 가장 자주 사용함
② 수식화
○ 단순 모델
Figure. 2. probit regression model
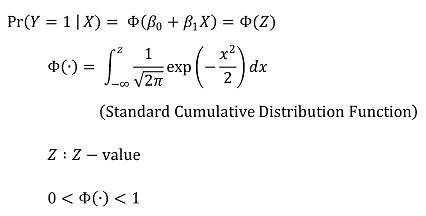
○ 다중 모델
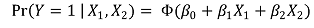
③ 효과(effect)
○ 수식화
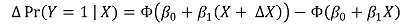
○ marginal effect

④ 통계적 추정
○ 각 계수의 추정량의 정확한 함수의 형태가 있는 것은 아님 : 수치해석을 통해 최대우도추정량을 구함
○ 일단 구해진 최대우도추정량은 일관성(consistency)과 정규근사성(asymptotically normality)을 만족
⑶ logistic regression model
① 수식화
○ 로지스틱 함수(logistic function)
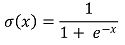
○ 모델링 : linear regression 형태인 βx + β0를 linking function인 로지스틱 함수에 넣음
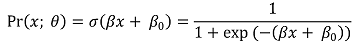
○ 로짓(logit, log-odd, logarithmic of odds ratio) : 승산비를 로그 변환한 것. 음의 무한대부터 양의 무한대까지 값을 가짐
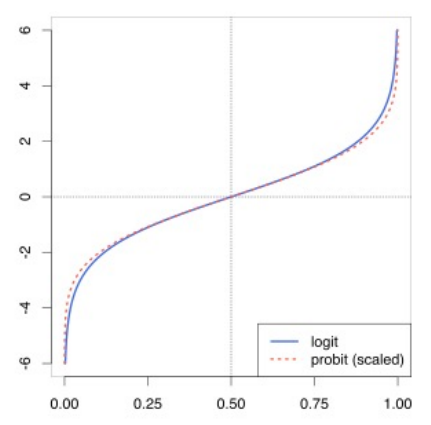
Figure. 3. logit 함수
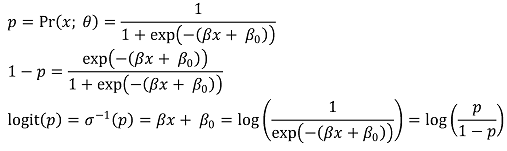
○ 로지스틱함수는 로짓 함수의 역함수
○ 로지스틱함수는 음의 무한대부터 양의 무한대까지의 값을 가지는 입력변수를 0 ~ 1 사이의 값을 가지는 출력변수로 변환한 것
② 최대우도 추정
○ 독립변수를 1차원 변수 xi가 아닌 다차원 변수 xi로 가정하고 베르누이 함수를 이용
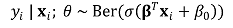
○ 우도함수 L(θ)와 로그우도함수 ℓ(θ)의 정의 : 여기서 정의된 L(θ)는 cross-entropy의 일종

○ 정리 : L(θ)와 ℓ (θ)는 convex function : 극소해는 local solution이 아니라 global solution이 됨. 증명은 다소 복잡
○ 단계 1. 그래디언트의 정의

○ 단계 2. 헤세 행렬의 정의
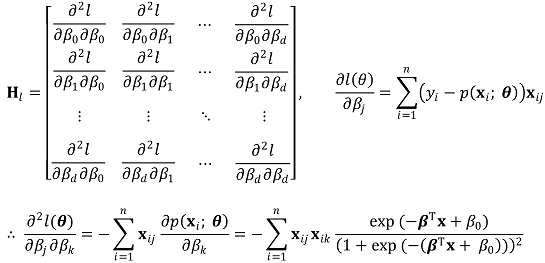
○ 단계 3. θk에 대하여 테일러 급수를 구하여 2차 근사식을 구하고 근사식의 극대해 θk+1 = θk + dk를 구함
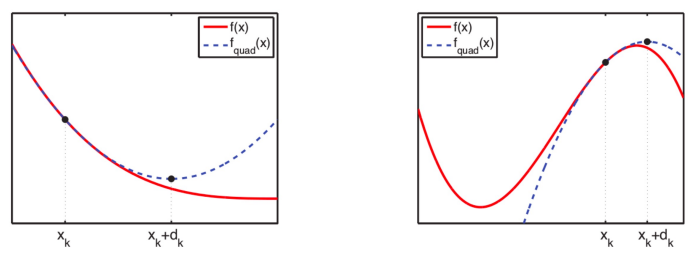
Figure. 4. 최대우도 추정과 테일러 급수의 관계
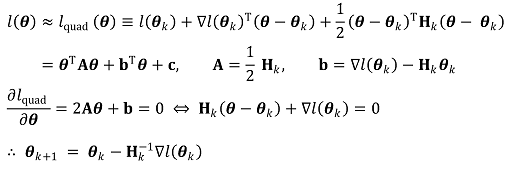
○ 단계 4. 뉴턴-랩슨법(Newton-Raphson method)처럼 θk를 업데이트하면 global maximum에 도달함
○ 이와 같이 수치해석으로 구할 뿐 각 계수의 추정량의 정확한 함수 형태가 있는 것은 아님
③ 일관성 증명에 대한 발상 (단, 기호가 위와 다를 수 있음에 유의)
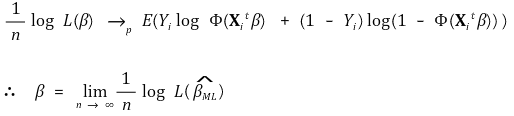
④ 정규근사성 증명에 대한 발상 (단, 기호가 위와 다를 수 있음에 유의)

⑤ 응용 : multiclass classification
○ 서론 : logistic regression은 binary classification이므로 이를 multiclass classification에 직접 이용할 수 없음
○ 방법 1. 1 vs {2, 3}을 한 후 2 vs 3과 같이 하는 방식
○ 방법 2. softmax 함수
○ 정의
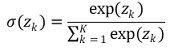
○ multiclass classification에서의 softmax 함수
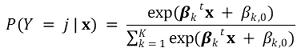
○ 증명 : logistic regression은 softmax 함수의 특수한 예임
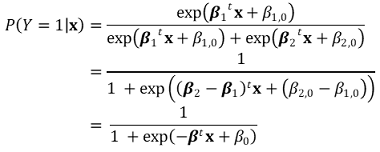
⑷ LPM, probit, logistic의 비교
① LPM, probit, logistic 간에 계수를 비교할 수 없음 : 모델이 다르므로
○ 예 1. probit regression model과 logistic regression model의 비교
○ 굉장히 유사한 플롯을 보여줌
Figure. 5. probit regression model과 logistic regression model의 비교
○ 계수 차이는 굉장히 크게 남 : 이 차이에 어떤 수학적 의미는 없음

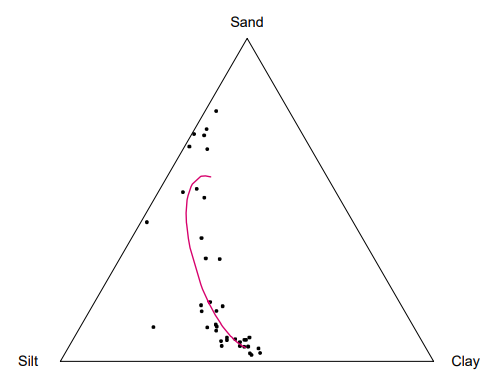
⑸ Dirichlet regression model
① 개요 : 위상(topology, simplex)을 고려하여 회귀 분석을 진행할 때 사용
Figure. 6. Dirichlet regression model이 적용되는 상황
② sample space : 각 항목별 비율 또는 확률을 나타내는 다차원 벡터
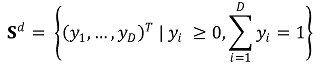
○ non-negative data
○ unit-sum
○ D : component의 개수, 즉 차원의 크기
○ d = D - 1
③ Dirichlet distribution : simplex를 분석할 수 있어서 주목받음
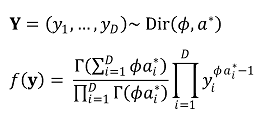
④ Dirichlet regression의 추정
○ Aitchison (2003)이 처음으로 log-ratio transformation을 도입
○ 로그우도함수 : n개의 데이터가 주어져 있을 때,
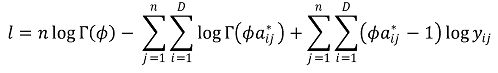
○ 로그우도함수에서 zero data가 문제가 됨
○ 해결책 1. zero data를 아주 작은 다른 값으로 치환 : Palarea-Albaladejo, Martín-Fernández 등이 제안
○ 해결책 2. zero data만을 따로 handling 하는 이중 모델을 사용 : Zadora, Scealy, Welsh, Stewart, Field, Bear, Billheimer 등이 제안
○ 해결책 3. zero data도 robust하게 적용할 수 있는 개선된 하나의 regression model을 사용 : Tsagris, Stewart 등이 제안
5. 상호작용(interaction) [목차]
⑴ 모델링
① interaction regressor 또는 interaction term을 도입
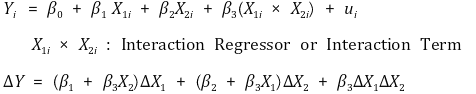
② 상호작용 항이 없는 모델과 계수를 비교할 수 없음
③ 셋 이상의 다중 상호작용도 정의할 수 있음
⑵ 효과(effect) : Xi의 단위 변화에 대한 Yi의 효과는 다음과 같음

⑶ 탄력성(elasticity)
① 직관적으로 기울기의 절대값이 큰 정도를 의미
② 미시경제학에서 탄력성은 기울기에 (-1)을 곱한 것을 의미
⑷ 응용 : 이진변수의 상호작용
① 모델링

② 효과 : X의 단위 변화에 따른 Y의 효과는 다음과 같음

③ H0 : Y가 D에 영향을 받지 않음은 β2 = β3 = 0을 검정하는 F 통계량 이용. determinant check
④ H0 : X의 단위 변화에 따른 Y의 효과가 D에 영향을 받지 않음은 β3 = 0을 검정하는 t 통계량 이용
⑤ D = 0인 회귀선과 D = 1인 회귀선을 통해 전체 회귀선을 구할 수 있음
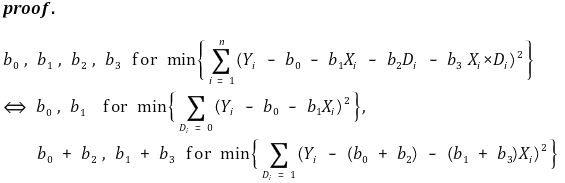
⑸ 응용 : 두 개의 이진변수(더미변수)의 상호작용
① 모델링
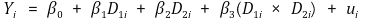
② D1, D2에 대한 2 × 2 테이블을 알면 회귀선 식을 유도할 수 있음
입력: 2019.06.21 12:10
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 5-2강. 거리함수와 유사도 (2) | 2023.10.24 |
|---|---|
| 【통계학】 14-5강. 런 검정(run test) (0) | 2023.09.22 |
| 【통계학】 14-8강. 윌콕슨 순위 검정(Wilcoxon Rank Test) (3) | 2021.05.10 |
| 【통계학】 14-2강. 단순 검정 (0) | 2021.04.13 |
| 【통계학】 5-1강. 이미지 유사성 비교 : SSIM (2) | 2021.02.19 |







최근댓글