14-10강. 우도비 검정과 Wilks’ phenomenon 증명
추천글 : 【통계학】 14강. 통계적 검정
1. 정리 [본문]
2. 증명 [본문]
3. 예제 [본문]
1. 정리 [목차]
⑴ 우도비 검정(likelihood ratio test) : 귀무가설 H0 : θ = θ0, 대립가설 H1 : θ ≠ θ0가 주어져 있을 때, 귀무가설 H0를 기각하는 조건, 즉 기각역을 다음과 같이 설정할 수 있음 (단, ℒ는 우도함수)

⑵ 일반화된 우도비 검정(generalized likelihood ratio test) : 우도비 검정에서 H0를 θ = θ0와 같이 단순 가설로밖에 정의할 수 없는 게 문제가 됨. 귀무가설 H0 : θ ∈ Θ0, 대립가설 H1 : θ ∉ Θ0와 같이 더 다채롭게 정의한 상황에 대하여 귀무가설 H0를 기각하는 조건, 즉 기각역을 다음과 같이 설정할 수 있음 (단, ℒ는 우도함수)

⑶ Wilk's phenomenon : n이 충분히 크면, θ = (θ1, ···, θk), 귀무가설 H0 : θ ∈ Θ0, 대립가설 H1 : θ ∉ Θ0에 대하여, -2 log λ(X1, ···, Xn)은 자유도가 ν인 카이제곱분포를 따름

⑷ 단순화된 Wilk's phenomenon : n이 충분히 크면, 귀무가설 H0 : θ = θ0, 대립가설 H1 : θ ≠ θ0, θ ∈ ℝ에 대하여, -2 log λ(X1, ···, Xn)은 자유도가 1인 카이제곱분포를 따름

2. 증명 [목차]
⑴ 단순화된 Wilk's phenomenon에 대해 증명
⑵ 테일러 전개(Taylor expansion)를 이용

3. 예제 [목차]
⑴ 예제 1. X1, ···, Xn ~ Poisson(λ)와 귀무가설 H0 : λ = λ0, H1 : λ ≠ λ0에 대하여 신뢰수준 α에 대한 기각역을 찾아라.
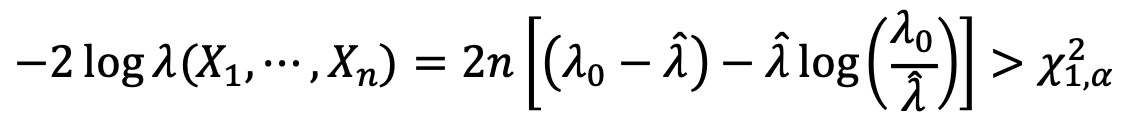
⑵ 예제 2. θ = (p1, ···, p5)에 대한 다항분포를 따르는 y1, ···, y5가 있어 L(θ) = p1y1 ··· p5y5와 같이 정의된다. 귀무가설 H0 : p1 = p2 = p3, p4 = p5와 대립가설 H1에 대하여, 신뢰수준 α에 대한 기각역을 찾아라.
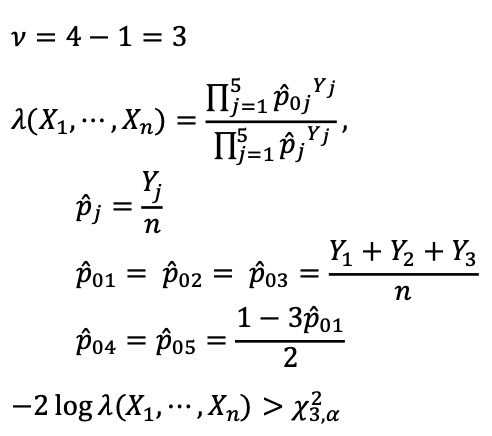
⑶ 예제 3. 카이제곱 단순적합도 검정 : 서로 다른 S개의 빈 (s = 1, ···, S)에 대해, 각 빈의 빈도수 Ns, null 확률 ps0, 전체 샘플수 n에 대해, 카이제곱 검정테스트 말고도 우도비 검정을 수행할 수 있다. 단, n → ∞에서 카이제곱 검정테스트 통계량과 우도비 검정 통계량이 동일하다.
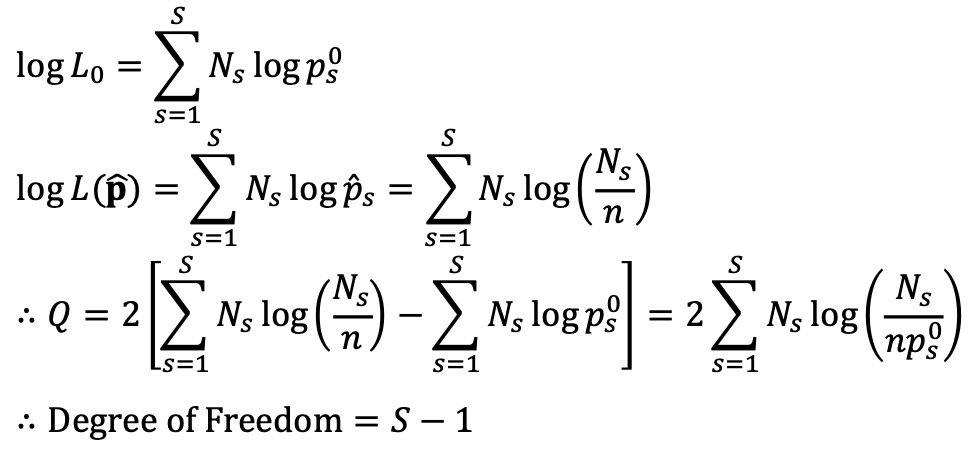
입력: 2024.09.24 22:10
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 18강. 회귀분석의 정규화 (2) | 2024.10.10 |
|---|---|
| 【통계학】 21강. 정보이론 (5) | 2024.10.07 |
| 【통계학】 Optimal Transport 및 Gromov-Wasserstein 거리 이해하기 (3) | 2023.11.04 |
| 【통계학】 5-2강. 거리함수와 유사도 (2) | 2023.10.24 |
| 【통계학】 14-5강. 런 검정(run test) (0) | 2023.09.22 |




최근댓글