통계학 기초 문제 [21-40]
추천글 : 【통계학】 통계학 목차
문제 21. 연속확률변수 X와 Y의 결합확률밀도함수가 다음과 같을 때, c, X와 Y의 주변확률분포, E[X], E[Y], V[X]를 구하여라.

1 = ∫0 to 2 ∫x to 2 cxy dydx = 2c ⇔ c = 0.5
E[X] = ∫0 to 2 ∫x to 2 0.5x2y dydx = 16/15
E[Y] = ∫0 to 2 ∫x to 2 0.5xy2 dydx = 8/5
E[X2] = ∫0 to 2 ∫x to 2 0.5x3y dydx = 4/3
∴ V[X] = E[X2] - (E[X])2 = 4/3 - (16/15)2 = 44/225
문제 22. 연속확률변수 X와 Y의 결합확률밀도함수가 아래와 같을 때, E[X], E[XY], Cov[2X, 3X], E[Y | X = 1/2]를 구하여라.

E[X] = ∫0 to 1 ∫0 to 1 (x2 + xy) dydx = 7/12
E[Y] = E[X] = 7/12
E[XY] = ∫0 to 1 ∫0 to 1 (x2y + xy2) dydx = 1/3
E[X2] = ∫0 to 1 ∫0 to 1 (x3 + x2y) dydx = 5/12
Cov[2X, 3X] = 6V[X] = 6(E[X2] - (E[X])2) = 6(5/12 - 49/144) = 11/24
E[Y | X = 1/2] = ∫0 to 1 y·(1/2 + y) dy / ∫0 to 1 (1/2 + y) dy = 7/12
문제 23. 이산확률변수 X와 Y의 결합확률질량함수(p.m.f)가 다음과 같을 때, c, P(X > Y), σX, Cov[X, Y]를 구하여라.

1 = f(1,0) + f(1,1) + f(1,2) + f(2,0) + f(2,1) + f(2,2) ⇔ c = 1/25
P(X > Y) = f(1,0) + f(2,0) + f(2,1) = (1+4+5) / 25 = 2/5
E[X] = 1 × (f(1,0) + f(1,1) + f(1,2)) + 2 × (f(2,0) + f(2,1) + f(2,2)) = 42/25
E[X2] = 1 × (f(1,0) + f(1,1) + f(1,2)) + 4 × (f(2,0) + f(2,1) + f(2,2)) = 76/25
σX = √( E[X2] - (E[X])2 ) = √( 76/25 - (42/25)2 ) = 0.4664762
E[Y] = 1 × (f(1,1) + f(2,1)) + 2 × (f(1,2) + f(2,2)) = 33/25
E[XY] = 1 × f(1,1) + 2 × f(1,2) + 2 × f(2,1) + 4 × f(2,2) = 54/25
Cov[X, Y] = E[XY] - E[X]·E[Y] = -0.0576
문제 24. (X, Y)의 결합밀도함수가 다음과 같을 때, c와 E(X | y = 2)를 구하여라.

1 = ∫0 to 1 ∫0 to ∞ ce-y dydx = c
E(X | y = 2) = ∫0 to 1 xe-2 dx / ∫0 to 1 e-2 dx = 1/2
문제 25. (X, Y)의 결합밀도함수가 다음과 같을 때, 상관계수를 구하여라.

E[X] = ∫0 to ∞ ∫x to ∞ xe-y dydx = 1
E[X2] = ∫0 to ∞ ∫x to ∞ x2e-y dydx = 2
E[Y] = ∫0 to ∞ ∫x to ∞ ye-y dydx = 2
E[Y2] = ∫0 to ∞ ∫x to ∞ y2e-y dydx = 6
∴ V[X] = E[X2] - (E[X])2 = 1
∴ V[Y] = E[Y2] - (E[Y])2 = 2
E[XY] = ∫0 to ∞ ∫x to ∞ xye-y dydx = 3
∴ COV[X, Y] = E[XY] - E[X]·E[Y] = 1
∴ Corr[X, Y] = COV[X, Y] / (σX · σY) = 1 / √2
문제 26. 확률변수 X와 Y는 독립이고, X ~ N(5, 22), Y ~ B(10, 1/2)일 때, P(5 < X < 10), E[XY - 2X - 1], V[X - Y - 1]을 구하여라.
N은 정규분포이고, B는 이항분포를 나타냄을 유의하자.
X와 Y는 독립이다.
P(5 < X < 10) = P(0 < Z < 2.5) = 0.4937903
E[XY - 2X - 1] = E[X]E[Y] - 2E[X] - 1 = 5 × (10 × 1/2) - 2 × 5 - 1 = 25 - 11 = 14
V[X - Y - 1] = V[X] + V[Y] = 4 + 10 × 1/2 × (1 - 1/2) = 4 + 2.5 = 6.5
문제 27. 다섯 장의 카드에 각각 1, 1, 2, 2 그리고 3을 적어 한 상자에 넣은 후 무작위로 2장을 선택한다. X는 2장의 합이고, Y는 두 수 중 최대 수일 때, X와 Y의 결합분포, Cov(X, Y), ρ(X, Y)를 구하여라.
| 1번째 \ 2번째 | 1 | 1 | 2 | 2 | 3 |
| 1 | X=2, Y=1 | X=2, Y=1 | X=3, Y=2 | X=3, Y=2 | X=4, Y=3 |
| 1 | X=2, Y=1 | X=2, Y=1 | X=3, Y=2 | X=3, Y=2 | X=4, Y=3 |
| 2 | X=3, Y=2 | X=3, Y=2 | X=4, Y=2 | X=4, Y=2 | X=5, Y=3 |
| 2 | X=3, Y=2 | X=3, Y=2 | X=4, Y=2 | X=4, Y=2 | X=5, Y=3 |
| 3 | X=4, Y=3 | X=4, Y=3 | X=5, Y=3 | X=5, Y=3 | X=6, Y=3 |
그러므로 X와 Y의 결합분포는 다음과 같이 나타낼 수 있다.
| X \ Y | 1 | 2 | 3 |
| 2 | 4/25 | 0 | 0 |
| 3 | 0 | 8/25 | 0 |
| 4 | 0 | 4/25 | 4/25 |
| 5 | 0 | 0 | 4/25 |
| 6 | 0 | 0 | 1/25 |
E[X] = 2 × 4/25 + 3 × 8/25 + 4 × 8/25 + 5 × 4/25 + 6 × 1/25 = 90/25
E[X2] = 4 × 4/25 + 9 × 8/24 + 16 × 8/25 + 25 × 4/25 + 36 × 1/25 = 352/25
V[X] = E[X2] - (E[X])2 = 1.12
E[Y] = 1 × 4/25 + 2 × 12/25 + 3 × 9/25 = 55/25
E[Y2] = 1 × 4/25 + 4 × 12/25 + 9 × 9/25 = 133/25
V[Y] = E[Y2] - (E[Y])2 = 0.48
E[XY] = 2 × 4/25 + 6 × 8/25 + 8 × 4/25 + 12 × 4/25 + 15 × 4/25 + 18 × 1/25 = 214/25
Cov[X, Y] = E[XY] - E[X]·E[Y] = 0.64
ρ[X, Y] = Cov[X, Y] / √( V[X]·V[Y] ) = 0.8728716
문제 28. 이산확률변수 X의 확률질량함수가 다음과 같을 때 E[X(6 - X)]을 구하여라.

E[X] = (12 + 22 + 32 + 42 + 52) / 15 = 11/3
E[X2] = (13 + 23 + 33 + 43 + 53) / 15 = 15
∴ E[X(6 - X)] = 6E[X] - E[X2] = 7
문제 29. 이산확률변수 X에 대하여, E[X] = 2와 E[X(X - 4)] = 5일 때, -4X + 12의 분산과 표준편차를 구하여라.
E[X] = 2
E[X2] - 4E[X] = 5 ⇔ E[X2] = 13
∴ V[-4X + 12] = 16V[X] = 16(E[X2] - (E[X])2) = 16(13 - 4) = 144
∴ σ = 12
문제 30. 확률변수 X는 이항분포(n = 10, p = 0.3)이고 Y는 포아송(λ = 2)이다. 이때 확률변수 X와 Y가 독립이라면 E[3X - 5Y + XY]를 구하여라.
E[3X - 5Y + XY] = 3E[X] - 5E[Y] + E[X]·E[Y] = 3 × 10 × 0.3 - 5 × 2 + (10 × 0.3) × 2 = 9 - 10 + 6 = 5
문제 31. 연속확률변수 X와 Y의 결합확률밀도함수가 다음과 같을 때, E(X | y = 1/2)를 구하여라.

E(X | y = 1/2) = ∫0 to 1 (3/2) · x · (x2 + (1/2)2) dx / ∫0 to 1 (3/2) · (x2 + (1/2)2) dx = 9/14
문제 32. X가 다음과 같은 확률밀도함수 f(x)를 가질 때, Y = e-X의 확률분포함수와 확률밀도함수를 구하여라.

확률분포함수 F(y) = Pr(Y ≤ y) (단, e-1 < y < 1) = Pr(X ≥ - ln y) = 1 + ln y
확률밀도함수 p(y) = d/dy F(y) = 1/y (단, e-1 < y < 1)
문제 33. 이산확률변수 X와 Y의 결합확률함수가 다음과 같을 때, 상수 k의 값과 X와 Y의 주변확률함수를 구하여라.

1 = k(12 + 12) + k(12 + 32) + k(22 + 32) = 2k + 10k + 13k = 25k ⇔ k = 1/25
P(X = 1) = 12/25
P(X = 2) = 13/25
P(Y = 1) = 2/25
P(Y = 3) = 23/25
문제 34. X와 Y가 E[X] = E[Y] = 1인 지수분포를 따르고 독립일 때, X + Y의 밀도함수를 구하여라.
p(x) = λe-λx, λ = 1
MX(t) = MY(t) = λ / (λ - t) = 1 / (1 - t)
MX+Y(t) = (1 / (1 - t))2 → 감마분포의 적률생성함수 (단, λ = 1, r = 2)
∴ P(X+Y = z; r, λ) = z exp(-z)
문제 35. X1과 X2의 결합 pdf가 다음과 같을 때, Y = g(X1, X2) = X1 + X2의 pdf를 구하여라.

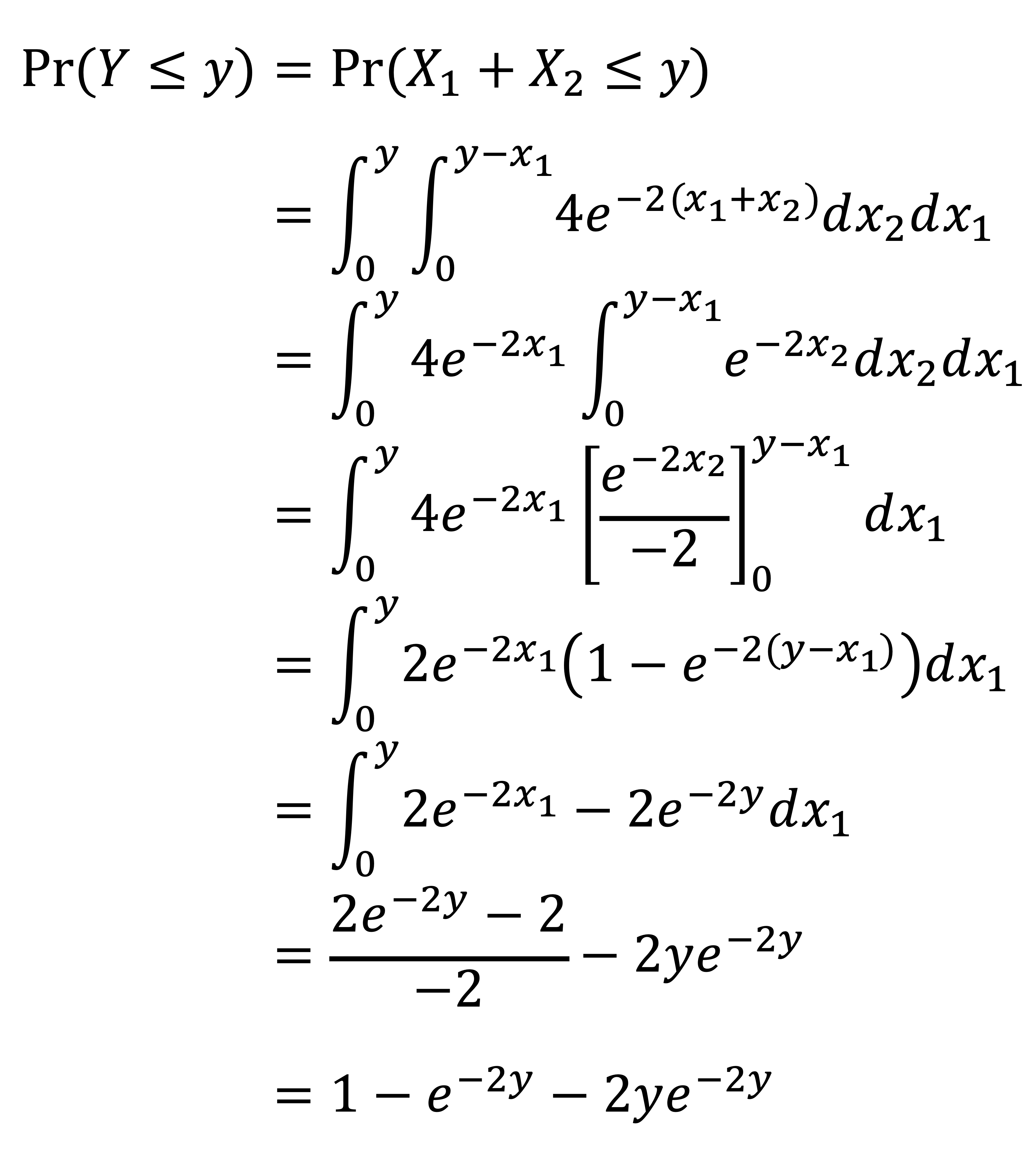
그러므로 Y의 PDF는 d/dy Pr(Y ≤ y) = 4y·e-2y
문제 36. X와 Y의 결합 확률 질량함수가 아래와 같을 때, c, fX(x), P(X + Y > 1), X와 Y는 독립인지 여부를 구하여라.

ex = ∑k=0 to ∞ xk / k! 이므로 1 = ∑∑ f(x, y) = c · ∑2x / x! · ∑2y / y! = ce4 ⇔ c = e-4
fX(x) = e-4 (2x / x!) ∑2y / y! = e-2 2x / x!
fY(y) = e-2 2y / y!
∴ f(x, y) = fX(x)·fY(y) ⇔ X와 Y는 독립
P(X + Y > 1) = 1 - P(X + Y ≤ 1) = 1 - (f(0, 0) + f(0, 1) + f(1, 0)) = 1 - 5e-4
문제 37. X가 분포함수 F를 가지는 확률변수일 때, 확률변수 X2의 확률분포함수와 확률밀도함수를 구하여라.
F(x) = Pr(X ≤ x)
확률분포함수 = Pr(X2 ≤ y) = Pr(-√y ≤ X ≤ √y) = F(√y) - F(-√y) (단, y ≥ 0)
확률밀도함수 = Pr(X2 = y) = d/dy Pr(X2 ≤ y) = ( F'(√y) + F'(-√y) ) / 2√y (단, y ≥ 0)
문제 38. X가 다음과 같은 확률밀도함수를 가지는 확률변수일 때, Y = X2의 확률밀도함수를 구하여라.

문제 39. 다음은 확률변수 X에 대한 분포표일 때, E[X], V[X], E[etX]를 구하여라.
| X | -2 | 0 | 1 | 5 |
| P(X = x) | 0.2 | 0.3 | 0.4 | 0.1 |
E[X] = -2 × 0.2 + 1 × 0.4 + 5 × 0.1 = 0.5
E[X2] = 4 × 0.2 + 1 × 0.4 + 25 × 0.1 = 3.7
V[X] = E[X2] - (E[X])2 = 3.7 - 0.25 = 3.45
E[etX] = e-2t × 0.2 + 0.3 + e-t × 0.4 + e-5t × 0.1
문제 40. P(H) = 3/4이고, P(T) = 1/4인 동전을 3번 던졌을 때, X를 연속되어 나오는 앞면의 횟수라 할 때, X의 기댓값, 분산, 표준편차를 구하여라.
P(X = 0) = (1/4)3 = 1/64
P(X = 1) = 3 · (3/4)1 · (1/4)2 = 9/64
P(X = 2) = 3 · (3/4)2 · (1/4) = 27/64
P(X = 3) = (3/4)3 = 27 / 64
E[X] = 1 × 9/64 + 2 × 27/64 + 3 × 27/64 = 9 / 4
E[X2] = 1 × 9/64 + 4 × 27/64 + 9 × 27/64 = 45 / 8
V[X] = E[X2] - (E[X])2 = 0.5625
σ = 0.75
입력: 2024.12.24 13:56
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 통계학 목차 (1) | 2025.01.09 |
|---|---|
| 【통계학】 통계학 기초 문제 [41-60] (6) | 2024.12.26 |
| 【통계학】 통계학 기초 문제 [01-20] (5) | 2024.12.24 |
| 【통계학】 14-10강. Cochran-Mantel-Haenszel (CMH) 검정 (7) | 2024.10.14 |
| 【통계학】 18강. 회귀분석의 정규화 (2) | 2024.10.10 |




최근댓글