통계학 기초 문제 [61-80]
추천글 : 【통계학】 통계학 목차
문제 61. 한 회사는 120의 자금을 마련하여, 다음 1년 동안 높은 성과를 달성한 직원들에게 일정 금액 C를 지급하고자 한다. 이 회사에는 총 20명의 직원이 있으며, 각 직원이 높은 성과를 달성할 확률은 2%이다. 또한, 직원들 각각의 높은 성과 달성 여부는 서로 독립적인 사건이다. 자금이 모든 높은 성과를 달성한 직원들에게 지급하기에 부족할 확률이 1% 미만이 되도록 하기 위해, C의 최댓값을 계산하시오.
P(X = k) = 20Ck·0.02k·0.9820-k
0.01 > P(kC > 120) = P(k > 120 / C) = P(k > 2) (∵ 일일히 계산)
∴ 2 ≤ 120 / C < 3 ⇔ 60 ≥ C > 40
∴ 60
문제 62. 한 회사는 제조 공장에서 발생하는 사고를 보장하는 보험에 가입했다. 매월 한 건 이상의 사고가 발생할 확률은 0.60이며, 각 월별 사고 발생 여부는 서로 독립적이다. 4번째 사고가 발생하기 전에 사고가 전혀 발생하지 않은 달이 최소 4번 이상 존재할 확률을 구하시오.
사고확률 p = 0.6, 무사고확률 q = 0.4라 하면, 4번째 사고가 나올 때까지의 무사고 횟수 Y가 음이항분포를 따른다.
P(Y = k) = k+4-1C4-1·p4·qk = k+3C3·(0.6)4·(0.4)k
∴ P(Y ≥ 4) = 1 - P(Y ≤ 3) = 1 - ∑(k=0 to 3) k+3C3·(0.6)4(0.4)k = 0.2898
문제 63. 축구동아리 SNUnited는 일요일 아침마다 두 팀으로 나눠 연습경기를 한다. n명이 일요일 축구모임에 참석하면 일단 무작위로 두 팀에게 똑같이 n/2명을 배정한다고 하자. 편의상 n은 짝수라고 하자. 그런 후 4차례에 걸쳐 각 팀에서 무작위로 한 명씩 뽑아 선수를 교환하여 각 팀의 최종멤버를 결정한다고 하자. 4차례에 걸친 선수교환이 이루어지기 전과 후 두 팀의 선수구성에 변화가 없을 확률을 구하시오.
4차례에 걸친 선수교환에 관한 전체 경우의 수는 (n/2)8이다.
경우 1. 4 vs 4
○ 왼쪽에서 한 좌석 Li만 4번 뽑힘 : (n/2)가지
○ 오른쪽에서 한 좌석 Rj만 4번 뽑힘 : (n/2)가지
○ 4라운드 모두 (Li, Rj) 고정으로 뽑히므로 라운드 배치 방법은 1가지
○ 합계 : (n/2)2
경우 2. 4 vs 2+2
○ 왼쪽에서 4번 뽑힐 좌석 선택 : (n/2)가지
○ 오른쪽에서 서로 다른 두 좌석 Rj1, Rj2을 각 2번씩 선택 : (n/2)C2가지
○ 그 두 좌석 중 어떤 것이 라운드 1, 2, 3, 4 중 어느 두 회차에 뽑히는 고르는 배열 : 4C2 = 6가지
○ 예를 들어, 팀 A에서 a와 팀 B에서 b1을 고르고, 그 다음 팀 B에서 b1과 b2를 고르고, 다시 b2와 b1을 고르고, 마지막으로 a와 b1을 고르는 식으로 하는 경우가 경우 2에 해당함
○ 합계 : (n/2) × (n/2)C2 × 6
경우 3. 2+2 vs 4
○ 경우 2의 대칭 상황이므로 (n/2) × (n/2)C2 × 6
경우 4. 2+2 vs 2+2
○ 왼쪽에서 두 좌석 간 2번 뽑힘 선정 : (n/2)C2가지
○ 오른쪽에서 동일 : (n/2)C2가지
○ 왼쪽 두 좌석 뽑히는 라운드 배열 6가지, 오른쪽 두 좌석도 배열 6가지
○ 전체 라운드 매칭은 라운드 번호 1, 2, 3, 4가 똑같이 동작하므로 6 × 6 = 36가지
○ 합계 : (n/2)C2·(n/2)C2·36
따라서 4차례 교환 후 팀 구성이 변화 없을 전체 경우의 수는 (n2 / 4)·(3n2/2 - 2)2 이다.
그러므로 4차례 교환 후 팀 구성이 변화 없을 확률은 16(3n2 - 4)2 / n6이다.
문제 64. 한 도시에서 일어난 강도 사건의 범인이 남긴 혈흔을 분석한 결과 범인의 DNA에 대한 일부 증거를 확보할 수 있게 되었다고 하자. 일단 담당 형사는 이 도시에 거주하는 100만 명 중 한 명이 범인이라는 점은 확실하다고 판단하고 있다. 이 도시에서 거주하고 있는 시민 중 10,000명은 범죄경력이 있는 전과자이며 나머지 990,000명은 전과경력이 전혀 없는 사람들이라고 한다. 범죄경력이 있는 시민이라면 그 시민이 범인일 확률이 α, 전과경력이 없는 시민이라면 그 시민이 범인일 확률이 β라고 담당 형사는 생각하고 있다. (이 때 담당형사는 α가 β보다 k(> 1)배 만큼 크다고 여기고 있다.) 만일 어떤 시민이 범인이라면 그의 DNA가 사건 현장에서 확보한 DNA와 일치하는 것으로 나타날 확률이 1이며 범인이 아닌 사람의 DNA가 범인의 것과 일치하는 것으로 나올 확률이 10-5라고 하자. 이미 DNA 정보를 확보하고 있는 전과자 10,000명의 DNA 정보를 검토해 본 결과 유일하게 J 한 사람만이 범인의 것과 DNA가 일치하는 것으로 나타났다. 여러분이 담당형사라면 이 정보들로부터 J가 이 강도 사건의 실제 범인일 확률이 얼마라고 생각하겠는가? 그 확률을 k만의 함수로 나타내시오.
P(경력) = 0.01, P(~경력) = 0.99
P(범인 | 경력) = α, P(범인 | ~경력) = β = α / k
P(범인) = 1 / 100만 = P(경력) × P(범인 | 경력) + P(~경력) × P(범인 | ~경력) = 0.01α + 0.99α / k
∴ α = k / (10000k + 990,000)
P(일치) = P(경력) × P(범인 | 경력) × P(일치 | 범인) + P(경력) × P(~범인 | 경력) × P(일치 | ~범인)
P(일치) + P(~경력) × P(범인 | ~경력) × P(일치 | 범인) + P(~경력) × P(~범인 | ~경력) × P(일치 | ~범인)
P(일치) = 0.01α + 0.01(1-α)10-5 + 0.99(α / k) + 0.99(1 - α / k)10-5
∴ P(범인 | 일치) = ( 0.01α + 0.99(α / k) ) / ( 0.01α + 0.01(1-α)10-5 + 0.99(α / k) + 0.99(1 - α / k)10-5 )
만약 k ≫ 1이면, P(범인 | 일치) = 0.01α / (0.01α + 0.01(1-α)10-5 + 0.99 × 10-5) ≈ 1
만약 k = 1이면, P(범인 | 일치) = α / (α + (1-α) × 10-5) ≈ 1 / 11
문제 65. 길이가 l km인 해변에 아이스크림 가게를 오픈하려고 한다. 아이스크림 가게의 위치는 일단 왼쪽 끝지점부터 오른쪽 끝지점 중 무작위 추첨으로 한 곳을 선택한 후 다시 왼쪽 끝지점부터 이 지점까지 중 무작위 추첨으로 한 곳을 선택한다고 한다. 최종적으로 선택된 지점이 왼쪽 끝지점부터 떨어져 있는 거리를 X라고 하자. 확률변수 X의 밀도를 구하시오.
처음 선택한 지점이 왼쪽 끝지점부터 떨어져 있는 거리를 U(u), 두 번째 선택한 지점이 왼쪽 끝지점부터 떨어져 있는 거리를 V(v)라고 하자.

fU(u) = 1/l
f(u, v) = f(u)·f(v | u) = 1 / ul
fV(x) = fX(x) = ∫(u = x to l) (1 / ul) du = ln (l / x) / l
문제 66. 두산 베어스는 매 경기마다 관객 전원에게 두산 출신 전설적인 야구 선수 6명의 피규어를 무작위로 하나씩 제공하는 행사를 진행하기로 했다. 이 소식을 듣자마자, 야구광이자 두산의 열혈팬인 용준은 6명의 피규어를 전부 수집하기로 마음먹었다. 용준이 6명의 피규어를 전부 수집할 때까지 관람하게 될 총 경기 수를 X라고 하자. 단, 피규어를 구할 수 있는 유일한 방법은 두산 경기를 관람하는 것뿐이라고 가정한다. X의 기댓값 E[X]를 구하시오.
문제 60을 참고하자.
E[X] = 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 = 2.45
문제 67. X1, X2, ···, Xn는 i.i.d인 확률변수이며 E[Xi] = μ이고 Var(Xi) = σ2이라고 하자. 그리고 X̄ = (1/n) ∑(i=1 to n) Xi라고 할 때 Cov(Xi - X̄, X̄)를 구하시오.
답은 0.
문제 68. 학교 셔틀버스 승강장에 시각 t ≥ 0까지 도착하는 학생들의 수는 λ·t를 파라미터로 하는 푸아송분포를 따른다고 하자. 그리고 첫 셔틀버스가 승강장에 도착하는 시각은 (0, T) 구간에서 균일분포를 따른다고 하자. 이 첫 셔틀버스에 탑승하는 학생의 수를 확률변수 X라고 할 때, 확률변수 X의 평균과 분산을 구하시오. 단, 학생들이 도착하는 시각과 첫 셔틀버스가 도착하는 시각은 독립적이라고 하자.
전확률의 법칙 : E[X] = E[E[X | t]] = E[λ·t] = λT / 2
전분산의 법칙 : Var(X) = E[Var(X | t)] + Var(E[X | t]) = E[λt] + Var(λt) = λT / 2 + λ2T2 / 12
문제 69. 관악 스포츠 센터에서는 매달 한 번씩 회원들의 운동화를 세탁해주는 서비스를 제공하고 있다. 그런데 이번 달에는 담당 직원의 부주의로 각 운동화의 주인에 대한 별도 표시 없이 세탁한 후 무작위로 회원들의 보관함에 돌려놓고 말았다. 이번 달에 이 세탁 서비스를 받은 전체 회원수는 n명이라고 하자. 자신의 운동화를 제대로 돌려받은 회원수를 확률변수 X라고 할 때, X의 분산 Var(X)을 구하시오.
Xi를 i번째 회원이 자신의 운동화를 제대로 돌려받은 경우 1, 그렇지 않은 경우 0이 되는 indicator 확률변수라고 하자.
X = X1 + ··· + Xn
E[Xi] = (n-1)! / n! = 1 / n
E[X] = E[X1] + ··· + E[Xn] = (1/n)·n = 1
E[Xi2] = 1 / n
E[XiXj] (단, i ≠ j) = (n-2)! / n! = 1 / (n2 - n)
Var(Xi) = E[Xi2] - (E[Xi])2 = 1 / n - 1 / n2 = (n-1) / n2
Cov(Xi, Xj) = E[XiXj] - E[Xi]E[Xj] = 1 / (n2 - n) - 1 / n2 = 1 / (n2(n-1))
Var(X) = n·Var(Xi) + 2∑i<j E[XiXj] = (n-1) / n + 2·nC2 / (n2(n-1)) = (n-1) / n + 1 / n = 1
문제 70. 확률변수 X와 Y는 독립이며 각각 표준정규분포를 따른다고 하자. 이제 새로운 확률변수 Z가 다음과 같이 정의된다고 하자.

확률변수 Z 역시 표준정규분포를 따른다는 사실을 보이시오. 단, 표준정규분포의 밀도를 전혀 이용하지 말고 표준정규분포의 특징과 그 외 이 문제에서 주어진 가정만으로 이 사실을 증명하시오.
P(X > 0) = P(X < 0) = 1/2, P(Y > 0) = P(Y < 0) = 1/2가 성립한다.
특정 x 값에 대하여 XY > 0일 확률과 XY < 0일 확률이 1/2이므로 Z = x 및 Z = -x에 각각 1/2씩 할당된다.
그리고 특정 -x 값에 대하여 비슷하게 Z = x 및 Z = -x에 각각 1/2씩 할당된다.
따라서 P(Z = x) = P(X = x)이므로 Z는 X와 같은 확률밀도함수를 가진다.
문제 71. (St. Petersburg paradox) 공정한 동전을 던지다가 처음으로 앞면이 나오는 순간 게임이 종료된다고 하자. 만약 처음으로 앞면이 나온 것이 n번째 던지기라면, 당신은 $2n을 얻게 된다. 확률변수 X를 당신이 얻게 되는 금액이라고 하면, P(X = 2n) = 1/2n이 된다. 이제 기대값 E[X]를 계산하라.
E[X]는 무한대이다.

기대값이 무한대라는 것은 맞지만, 현실적인 의사 결정에서는 그대로 적용하기 어렵다는 것이 핵심 문제이다.
문제 72. (카지노의 전략) 우리는 $1을 가지고 게임을 시작한다. 매번 베팅할 때, 베팅한 금액만큼을 얻을 확률이 0.51이고, 베팅한 금액만큼을 잃을 확률이 0.49이다. 즉, 약간 우리에게 유리한 확률로 진행되는 게임이다. 이 게임에서 최대한 빠르게 돈을 벌 수 있는 전략을 찾아보라.
어떤 사람이 현재 자금 M의 x%를 베팅한다고 가정하자.
이 경우, 다음 게임에서 그가 가질 자금은 다음과 같이 표현될 수 있다 (단, p = P(승리) = 0.51).

도박에서 시행 횟수를 n이라 하자.
그러면 n번째 시행 후 그의 자금은 초기 자금 M0에 대해 다음과 같이 주어진다.
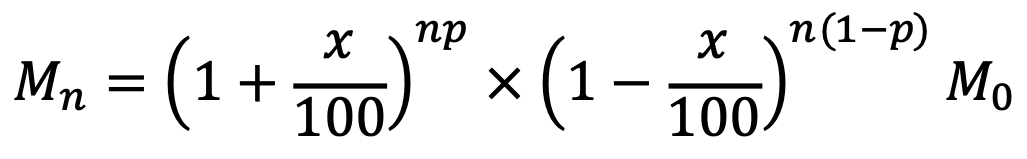
따라서 Mn의 최댓값을 구하기 위해 Mn의 극값을 구하자.

이를 Kelly criterion이라고 한다. 즉, 원래 자금의 f* = (p - q) / b (단, p = P(승리), q = P(실패)) 비율로 베팅해야 한다.
이때, b는 net odds로, 이 문제에서 X를 베팅하는만큼 승리 시 X를 얻게 되므로 b = 1이 된다.
참고로, x = 2에서 Mn의 2차 도함수가 음수이므로 Mn은 x = 2에서 극댓값을 가진다.

문제 73. 주어진 표본으로부터 중위값에 대한 신뢰구간을 구하는 방법을 기술하여라.
k번째 순서 통계량 X(k), 중위값 θ에 대하여 다음 식을 확인하자. 단, Bin은 이항분포이다.

따라서 k < ℓ 에 대하여 다음이 성립한다.

qk ≥ 1 - α/2 가 되도록 하는 가장 큰 k를 선택하고, qk ≤ α / 2 가 되도록 하는 가장 작은 ℓ을 선택하자.
그러면, 우리는 θ에 대한 신뢰수준 (1−α)의 신뢰구간(CI)을 얻을 수 있다.
문제 74. A 매장은 평균적으로 시간당 8명의 고객이 방문하고, B 매장은 시간당 6명의 고객이 방문한다. 두 매장의 고객 수는 서로 독립적이라고 가정한다. 다음 6시간 동안 A 매장이 B 매장보다 최소한 10명 더 많은 고객을 받을 확률은 얼마인가?
중심극한정리를 이용하자.

참고로, 두 독립 푸아송 확률변수 X∼Pois(λ1)과 Y∼Pois(λ2)의 합 X+Y는 푸아송 분포 Pos(λ1+λ2)를 따른다.
또한, 두 독립 푸아송 확률변수 X∼Pois(λ1)과 Y∼Pois(λ2)의 차 X−Y가 스켈럼 분포 Skellam(λ1, λ2)를 따른다.
문제 75. For two events E and F, we know that P(E, F) = 0.576, P(E | F) = 0.72, and P(F | E) = 0.9.
⒜ Find P(E).
⒝ Find P(F).
⒞ Find P(E ∪ F).
⒟ Find P(Ec ∪ Fc).
⒠ Find P(Ec ∩ Fc).
⒡ Find P(Ec | F).
⒢ Are E and F independent? Why?

문제 76. Urn A has 7 blue and 4 maize balls. Urn B has 12 blue and 9 maize balls. We flip a fair coin. If the outcome is heads, then a ball from urn A is selected, whereas if the outcome is tails, then a ball from urn B is selected. Suppose that a blue ball is selected. What is the probability that the coin landed heads?

문제 77. A new medical test has been designed to detect the presence of the mysterious Pumpkinification disease. Among those who have the disease, the probability that the disease will be detected by the new test is 0.74. However, the probability that the test will erroneously indicate the presence of the diease in those who do not actually have it is 0.12. It is estimated that 12% of the population who take this test have the disease. If the test administered to an individual is positive, what is the probability that the person actually has the disease?

문제 78. The joint probability mass function of X and Y is given by
p(1,1) = 0.35, p(2,1) = 0.05, p(3,1) = 0.1,
p(1,2) = 0.05, p(2,2) = 0.05, p(3,2) = 0.05,
p(1,3) = 0.1, p(2.3) = 0.1, p(3,3) = 0.15.
⒜ Compute the probability P(X + Y > 5).
⒝ Compute the probability P(X = Y | Y > 1).
⒞ Find the marginal pmf of X.
⒟ Compute E(X).
⒠ Are X and Y independent? Why?
⒡ Find the conditional pmf of Y given X = 3.

문제 79. The random variables X and Y have the following joing density function (where c is a constant):

⒜ Find the value of c.
⒝ Compute the probability P(Y > X). (Hint: consider the region y - x > 0.)
⒞ Are X and Y independent? Why?
⒟ Compute Var(Y).

문제 80. Two random variables X and Y are independent and have E(X) = 3, E(Y) = -1, Var(X) = 4, Var(Y) = 5.
⒜ Compute E(3X - 2Y + 7).
⒝ Compute Var(3X - 2Y+ 7).
⒞ Compute Cov(X, Y).
⒟ Compute E(3X2Y). (Hint: this is slightly trickier; you should use that Var(X) = 4.)

입력: 2025.02.17 22:13
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 통계학 기초 문제 [81-100] (0) | 2025.04.23 |
|---|---|
| 【통계학】 14-7강. Kolmogorov-Smirnov 검정 (0) | 2025.03.24 |
| 【통계학】 통계학 목차 (1) | 2025.01.09 |
| 【통계학】 통계학 기초 문제 [41-60] (6) | 2024.12.26 |
| 【통계학】 통계학 기초 문제 [21-40] (2) | 2024.12.25 |




최근댓글