통계학 기초 문제 [41-60]
추천글 : 【통계학】 통계학 목차
문제 41. 게임자가 두 개의 동전을 던질 때, 앞면이 2번 나오면 5파운드를 얻고, 한 번만 앞면이 나오면 2파운드를 얻으며 앞면이 전혀 나오지 않으면 1파운드를 얻는다. 기댓값을 구하여라.
최종적으로 얻게 될 금액에 대한 확률변수를 X라 하자.
P(X = 5) = 1/4
P(X = 2) = 1/2
P(X = 1) = 1/4
E[X] = 5 · 1/4 + 2 · 1/2 + 1 · 1/4 = 5/2
문제 42. 한 동전을 세 번 던질 때, 첫 번째에서 앞면이 나오면 X는 0이고, 뒷면이 나오면 1이라 하며, Y는 나타나는 앞면의 수라고 할 때, X와 Y의 분포, X와 Y의 결합분포, Cov(X, Y)를 구하여라.
P(X = 0) = 1/2
P(X = 1) = 1/2
P(Y = 0) = 1/8
P(Y = 1) = 3/8
P(Y = 2) = 3/8
P(Y = 3) = 1/8
X와 Y의 결합확률분포는 다음 표를 통해 나타낼 수 있다.
| X \ Y | 0 | 1 | 2 | 3 |
| 0 | 1/8 | 2/8 | 1/8 | 0 |
| 1 | 0 | 1/8 | 2/8 | 1/8 |
E[X] = 1/2
E[Y] = 3/2
E[XY] = 1 · 1/8 + 2 · 2/8 + 3 · 1/8 = 1
∴ Cov[X, Y] = E[XY] - E[X]·E[Y] = 1 - 3/4 = 1/4
문제 43. 연속확률변수 X가 다음과 같을 때, E[-X - 1], V[-X - 1]을 구하여라.
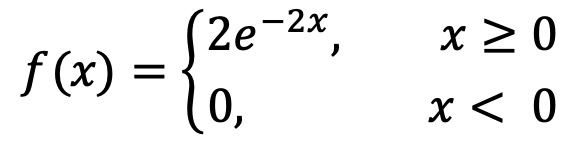
E[X] = ∫0 to ∞ 2xe-2x dx = 1/2
E[X2] = ∫0 to ∞ 2x2e-2x dx = 1/2
E[-X - 1] = -E[X] - 1 = -3/2
V[-X - 1] = V[X] = E[X2] - (E[X])2 = 1/2 - 1/4 = 1/4
문제 44. 3명을 한 줄로 세우는 경우의 수는?
3P3 = 3! = 6
문제 45. 4명 중 반장, 부반장을 뽑는 경우의 수는?
4P2 = 4 × 3 = 12
문제 46. 1, 2, 3, 4, 5의 숫자가 각각 하나씩 적힌 5장의 카드 중에서 서로 다른 3장을 뽑아 세 자리 자연수를 만드는 경우의 수는?
5P3 = 5 × 4 × 3 = 60
문제 47. 다음 그림과 같이 3장의 글자 카드가 있다. 이 중에서 서로 다른 2장의 카드를 택하여 일렬로 나열하는 경우의 수는?

3P2 = 3 × 2 = 6
문제 48. 다음 그림은 어느 하계 올림픽 경기 종목 중 4개의 종목을 나타낸 것이다. 이 4개의 종목에서 서로 다른 2개의 종목을 택하여 일렬로 나열하는 경우의 수는?
4P2 = 4 × 3 = 12
문제 49. 그림과 같이 3곳을 모두 여행하는 계획을 세우려고 한다. 여행 순서를 정하는 경우의 수는? (단, 한 번 여행한 곳은 다시 여행하지 않는다.)
3P3 = 3! = 6
문제 50. 대한민국, 독일, 미국, 영국, 일본, 중국, 프랑스, 호주 8개의 국가대표 농구 팀이 농구 경기를 하려고 한다. 1) 8팀 중 4팀을 고르는 경우의 수는? 2) 각 조당 4팀씩 A조와 B조로 나누는 경우의 수는? 3) 유럽 팀에서 1팀, 비유럽 팀에서 3팀을 고르는 경우의 수는? (단, 독일, 영국, 프랑스가 유럽 팀이다.)
8팀 중 4팀을 고르는 경우의 수 = 8C4 = 70
각 조당 4팀씩 A조와 B조로 나누는 경우의 수 (두 조가 구별되는 경우) = 8C4 = 70
각 조당 4팀씩 A조와 B조로 나누는 경우의 수 (두 조가 구별되지 않는 경우) = 70/2 = 35
유럽 팀에서 1팀, 비유럽 팀에서 3팀을 고르는 경우의 수 = 3C1 × 5C3 = 30
문제 51. 서로 다른 9개의 과자 중에서 6개를 고르는 방법의 수는?
9C6 = 9C3 = 84
문제 52. 4명 중에 봉사자 2명을 뽑는 경우의 수는?
4C2 = 6
문제 53. 그림과 같이 4개의 민속놀이가 있다. 이 중에서 서로 다른 2개의 민속놀이를 선택하는 경우의 수는?
4C2 = 6
문제 54. 그림과 같이 5개의 정다면체가 있다. 이 5개의 정다면체에서 서로 다른 2개의 정다면체를 선택하는 경우의 수는?
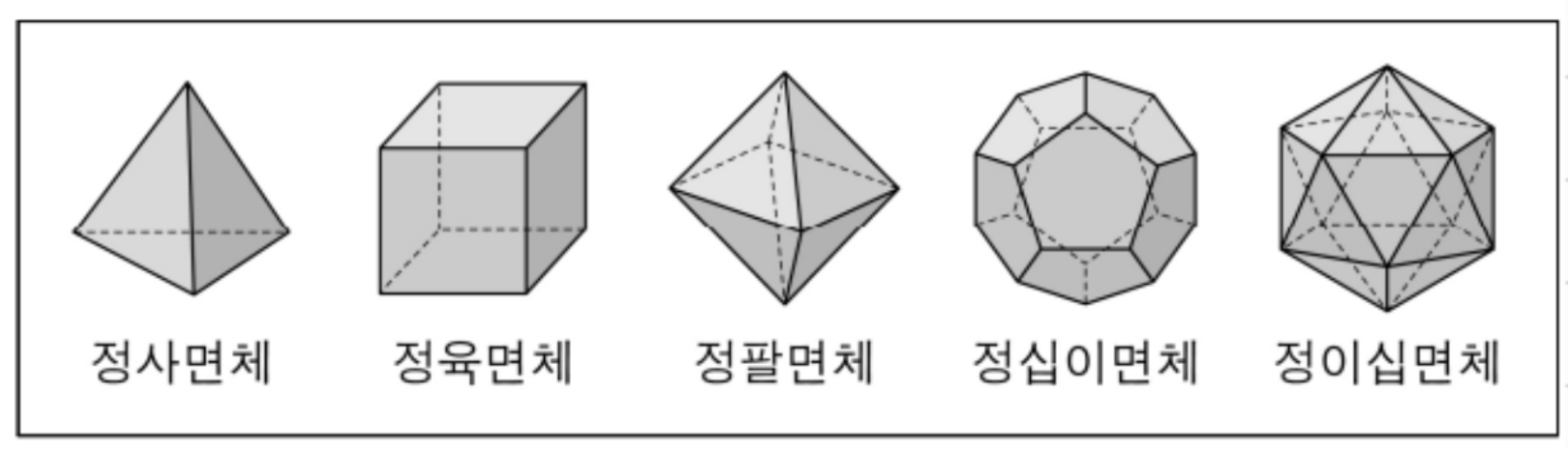
5C2 = 10
문제 55. 그림과 같이 4종류의 꽃이 있다. 이 중에서 서로 다른 3종류의 꽃을 선택하는 경우의 수는?
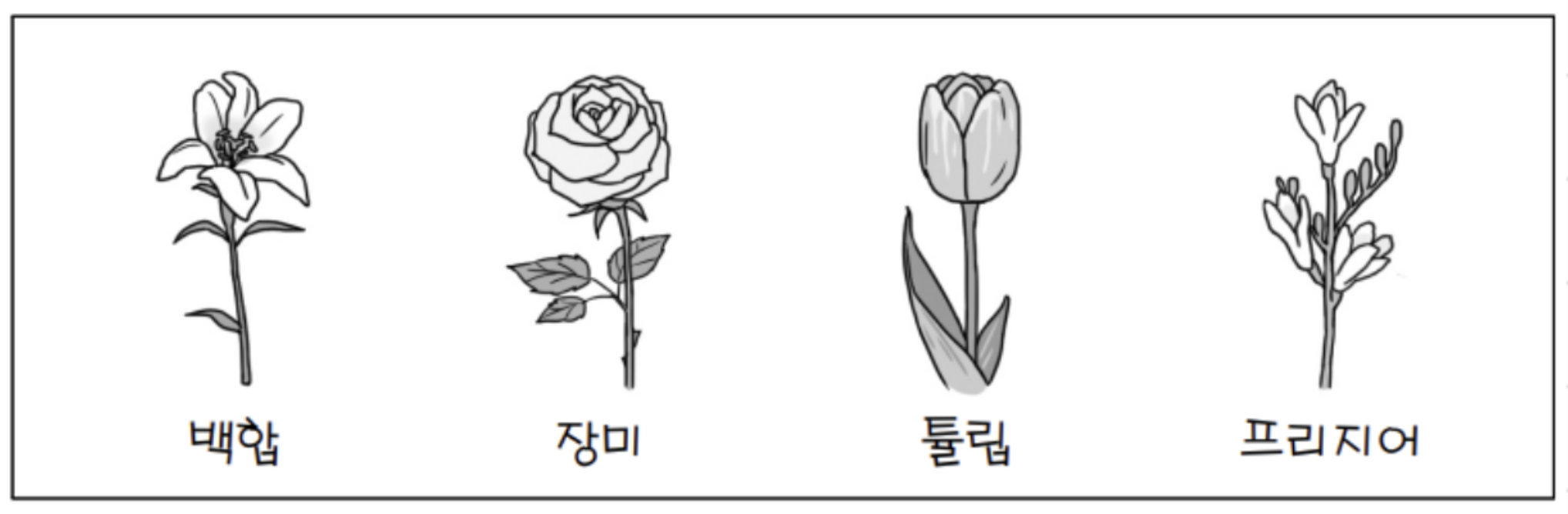
4C3 = 4
문제 56. (생일 문제, birthday problem) 한 그룹 안에서 두 사람이 같은 생일을 가질 확률이 최소 50%가 되려면 그룹에 최소 몇 명이 있어야 하는가?
Ak를 k번째 사람이 이전의 k-1번째 사람들과 다른 생일을 갖는 경우라고 정의하자.
만약 n명의 사람이 있다면, 어느 한 쌍도 같은 생일을 가지지 않을 확률은 다음과 같다.
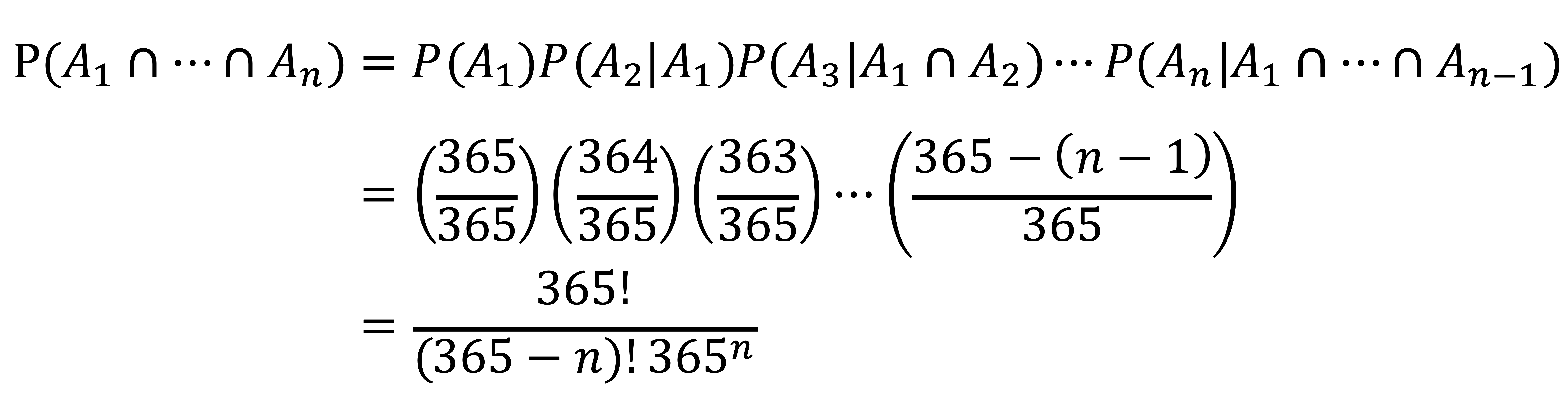
그러므로 1 - P(A1 ∩ ··· ∩ An) ≥ 0.5 ⇔ n ≥ 23을 얻을 수 있다.
문제 57. Find the expected number of runs of consecutive red cards when the 52 cards in a deck are turned up in random order.
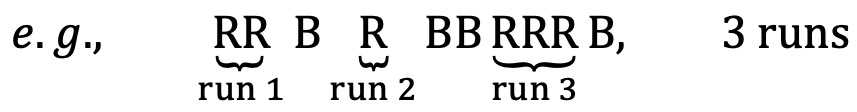
Let Ai = { ith card starts a run of red cards }, Bi = { ith card is black }, Ri = { ith card is red }.
A1 occurs if the first card is red, so P(A1) = P(R1) = 1/2
For 2 ≤ i ≤ 52, Ai occurs if the ith card is red and (i-1)st is black, so
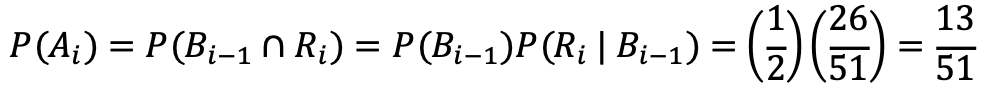
Thus, the expected number of runs of consecutive red cards is
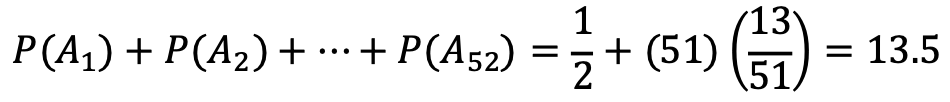
문제 58. Draw 6 balls from an urn containing 10 white balls and 10 black balls. Find the expected value and variance of the number of white balls drawn.
Let X be the number of white balls drawn.
Then, X = X1 + X2 + ··· + X6, where
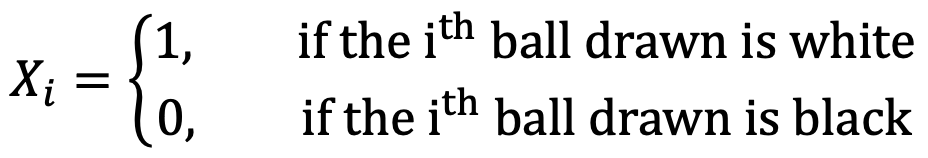
We have P(Xi = 1) = P(Xi = 0) = 1/2 for i = 1, ····, 6.
So E[Xi] = 1/2 and Var(Xi) = 12·(1/2) - (1/2)2 = 1/4.
Therefore, E[X] = E[X1 + ··· + X6] = E[X1] + ··· + E[X6] = 6·(1/2) = 3.
If i < j, then E[XiXj] is the probability that the ith and jth balls are both white, which is (1/2)·(9/19) = 9/38.
Therefore,
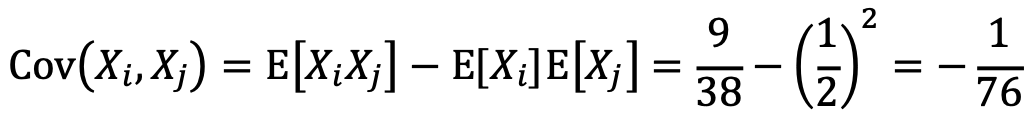
Thus,
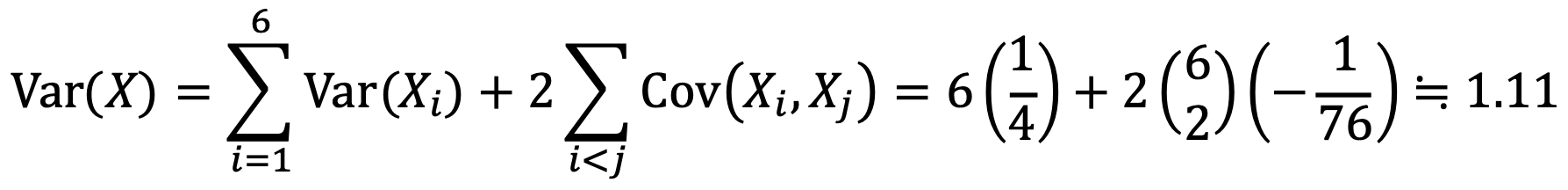
문제 59. We have two boxes, each containing 10 matches. We pick matches one at a time, each time choosing the box from which we pick the match at random. What is the probability that there are 3 matches left when one box empties?
Lable the boxes A and B. For box A to empty when box B has 3 matches left, we must pick 9 of the first 16 matches from box A and the 17th from box A. This event happens with 16C9 out of the 217 sequences of 17 A's and B's, so the probability is
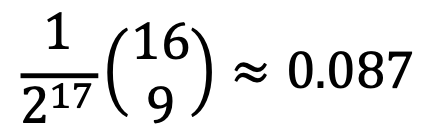
Box B could also empty first, so the probability that 3 matches are left when one box empties is
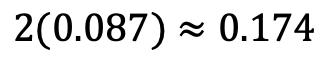
문제 60. Suppose a spinner picks a value from 1, 2, 3, 4 each with probability 1/4 and it is repeatedly spun until each of the numbers 1 through 4 is spun. What is the mean number of spins?
When we have seen k distinct numbers, let Xk,k+1 be the number of spins between seeing the k-th new number and seeing the (k+1)-th new number. e.g., if we spin the sequence

Then the total number of spins to see all 4 numbers at least once is 1 + X1,2 + X2,3 + X3,4.
So by the linearity of expected value, the average number of spins to see all N numbers at lease once is
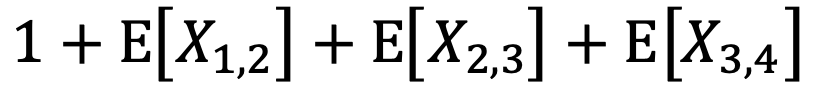
Without loss of generality, suppose that we have already seen the numbers 1, 2, ···, k. Then spinning any of the numbers k+1, ···, 4 would consitute seeing a new number. Then on a given spin, the probability of seeing a new number is then (4 - k) / 4 and the probability of landing on a number we have already seen is k/4. If Xk,k+1 = ℓ, then on ℓ - 1 consecutive spins, we landed on previously seen numbers, and the ℓ-th spin, we saw a new number, which implies that for ℓ = 1, 2, ···,
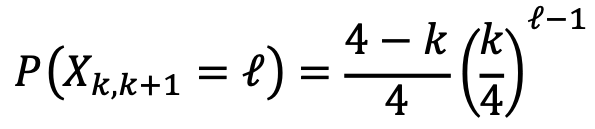
i.e. Xk,k+1 is geometric with p = (4 - k) / 4. Hence E[Xk,k+1] = 4 / (4 - k) which implies the average number of spins to see all N numbers at least once is
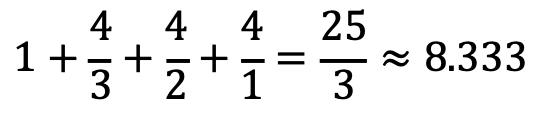
입력: 2024.12.25 10:37
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 통계학 기초 문제 [61-80] (0) | 2025.02.18 |
|---|---|
| 【통계학】 통계학 목차 (1) | 2025.01.09 |
| 【통계학】 통계학 기초 문제 [21-40] (2) | 2024.12.25 |
| 【통계학】 통계학 기초 문제 [01-20] (5) | 2024.12.24 |
| 【통계학】 14-10강. Cochran-Mantel-Haenszel (CMH) 검정 (7) | 2024.10.14 |




최근댓글