통계학 기초 문제 [81-100]
추천글 : 【통계학】 통계학 목차
문제 81. In the coin example from class - where the probability of a coin to show heads is a random variable Θ with density p(θ) = θeθ for 0 < θ < 1 - we now toss the coin two times. Say that X is a Bernoulli variable for the first coin toss, and Y is a Bernoulli variable for the second coin toss. Compute P(Y = 1 | X = 1), i.e., the conditional probability that the second toss shows heads given that the first toss showed heads.
Hint: this question requires little computation but a bit of thinking. You should use one of the conditioning formulas to condition on the possible values of Θ, and the fact the outcome of the first coin toss and of the second coin toss are conditionally independent given Θ = θ.

문제 82. Five people each call a plumber on one of four randomly chosen days. What is the probability that the plumber has at least one day with no calls?
Let Ai = {no call on day i}.
We want to find P(A1 ∪ A2 ∪ A3 ∪ A4).
We have P(Ai) = 35 / 45 ≃ 0.237.
If i < j, then P(Ai ∩ Aj) = 25 / 45 ≃ 0.031.
If i < j < k, then P(Ai ∩ Aj ∩ Ak) = 1 / 45 ≃ 0.001.
Also, P(A1 ∩ A2 ∩ A3 ∩ A4) = 0.
By the inclusion-exclusion formula, P(A1 ∪ A2 ∪ A3 ∪ A4) ≃ 4C1·0.237 - 4C2·0.031 + 4C3·0.001 - 0 = 0.766.
문제 83. (매칭 문제) We have n people, each of whom owns a hat. If we assign the n hats to the n people at random, what is the probability that someone gets their own hat?
Let Ai = {ith person gets back own hat}.
We want to find P(∪i=1 to n Ai).
There are n! ways of assigning hats to people.
The number of assignments such that the people numbered i1, ···, ik gets their own hat is (n-k)!.
Thus,
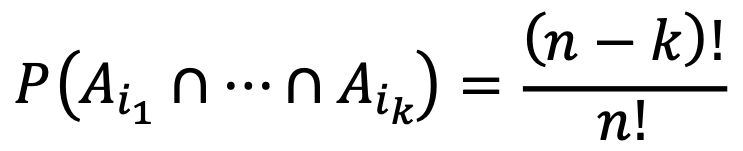
There are nCk ways to choose the k people, so
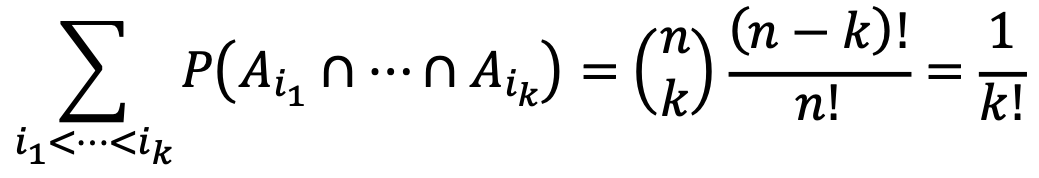
By the inclusion-exclusion formula,
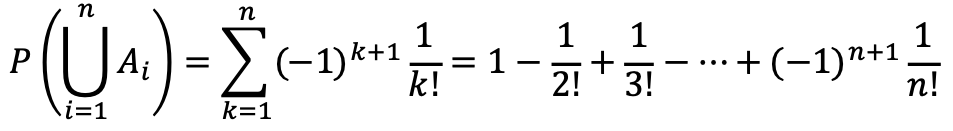
문제 84. Suppose accidents occur on a stretch of road, on average, once every 3 months. What is the probability that it will be between 7 and 9 years before there are 30 accidents?
Let Xi be the time in months before the first accident.
For i ≥ 2, let Xi be the time in months between the (i-1)st and the ith accidents.
The time before there are 30 accidents is S = X1 + ··· + X30.
Note that X1, X2, ···, X30 are iid and Xi have an exponential distribution with parameter λ = 1/3.
E[Xi] = 1 / λ = 3 and Var(Xi) = 1 / λ2 = 9.
Thus, E[S] = (30)(3) = 90 and Var(S) = (30)(9) = 270.
By the Central Limit Theorem, Z = (S - 90) / √270 ~ N(0, 1).
The Probability that it takes between 7 and 9 years to get 30 accidents is
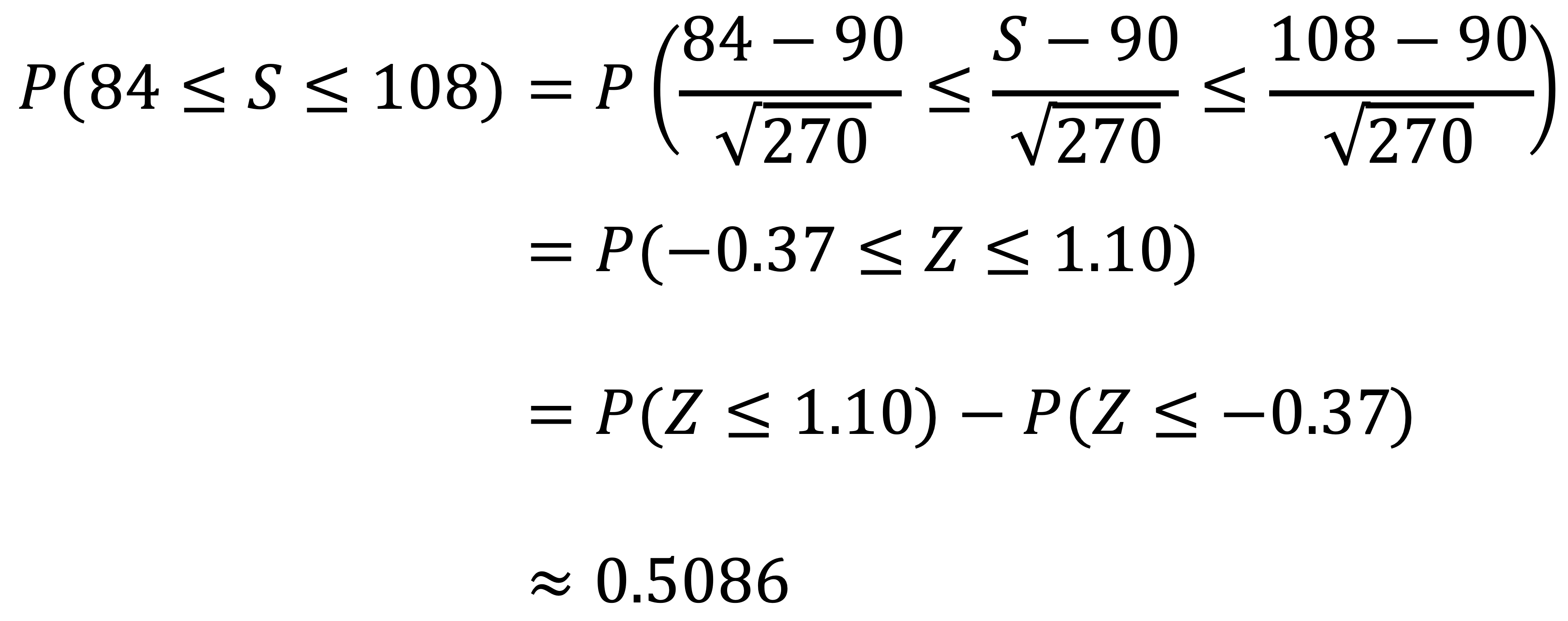
입력: 2025.04.23 09:57
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 14-7강. Kolmogorov-Smirnov 검정 (0) | 2025.03.24 |
|---|---|
| 【통계학】 통계학 기초 문제 [61-80] (0) | 2025.02.18 |
| 【통계학】 통계학 목차 (1) | 2025.01.09 |
| 【통계학】 통계학 기초 문제 [41-60] (6) | 2024.12.26 |
| 【통계학】 통계학 기초 문제 [21-40] (2) | 2024.12.25 |

최근댓글