【대수경】 제 42회 전국 대학생 수학 경시대회 제 1 분야
제 42회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 42회 전국 대학생 수학경시대회
제 1 분야
2024년 11월 2일 (10:30 - 13:00)
1. 다음 행렬 A에 대하여 등식 A5 = aA2 + bA + cI가 성립하도록 하는 실수 a, b, c를 구하여라. (단, I는 3 × 3 단위행렬)

Solution.
다음 식을 발견할 수 있다.

∴ A5 = A2 × (-3A) = (-3)2 A이므로 a = 0, b = 9, c = 0
2. 3차원 좌표공간에서 식 4z2 = x2 + y2 - 1로 주어진 곡면을 S라 하자. 곡면 S가 점 P(1, 2, 1)을 지나는 직선을 정확히 두 개 포함하고 있음을 보이고, 두 직선이 이루는 예각을 θ라 할 때 cos θ의 값을 구하여라.
Solution.
S : 4z2 = x2 + y2 - 1을 시각화한 결과는 다음과 같다.
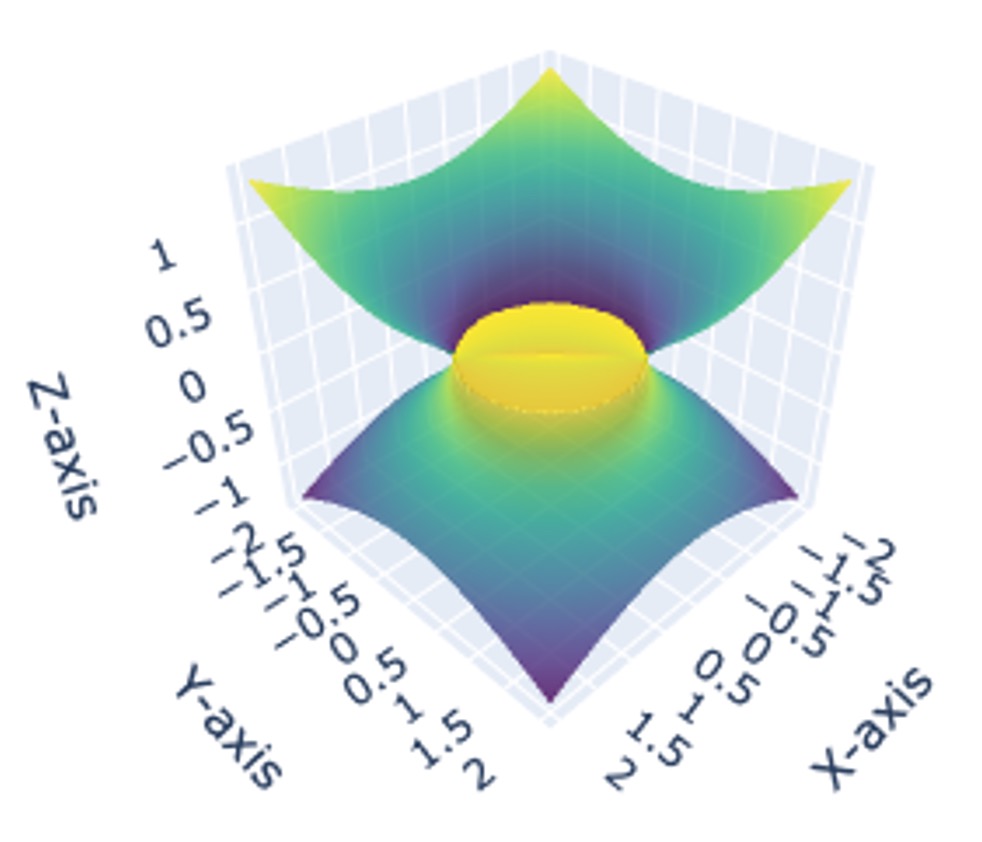
점 P(1, 2, 1)을 지나는 직선을 (at + 1, bt + 2, ct + 1), t ∈ ℝ로 둘 수 있으므로,
4(ct + 1)2 = (at + 1)2 + (bt + 2)2 - 1 ⇔ 4c2 = a2 + b2 (식 1), 8c = 2a + 4b (식 2)
(a, b, c)를 정규화하기 위해 a2 + b2 + c2 = 1 (식 3)으로 두고, 방향 벡터가 양쪽이 모두 가능하므로 c ≥ 0 (식 4)으로 제한하자.
(식 1)과 (식 2)로부터 c2 = 1/5를 얻을 수 있고, (식 4)로부터 c = √(1/5)를 얻을 수 있다.
a2 + b2 = 4/5로부터 a = √(4/5) cosφ, b = √(4/5) sinφ로 둘 수 있다.
2a + 4b = 2√(4/5) cosφ + 4√(4/5) sinφ = √((2√(4/5))2 + (4√(4/5))2) sin(φ+α) = 4sin(φ+α) = 8c = 8/√5를 얻을 수 있다.
4 > 8/√5이므로 (a, b, c) = (√(4/5) cosφ, √(4/5) sinφ, √(1/5))가 정확히 2개 존재한다.
이제 해의 개수를 정확하게 파악하기 위해 별도로 도입한 (식 3), (식 4)를 무시하고 (식 1), (식 2)에만 집중하자.
그러면 (a, b, c) = (0, 2, 1), (8, 6, 5)를 쉽게 찾을 수 있다. (각주 : 쉽게 찾을 수 없다면 위에서 구한 φ 및 α로 해를 결정할 수 있다.)
따라서 cosθ는 다음과 같다.
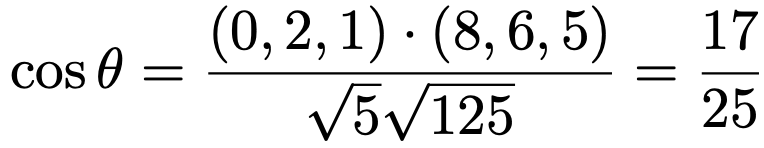
3. 다음 식을 만족하는 실수 N을 구하여라.
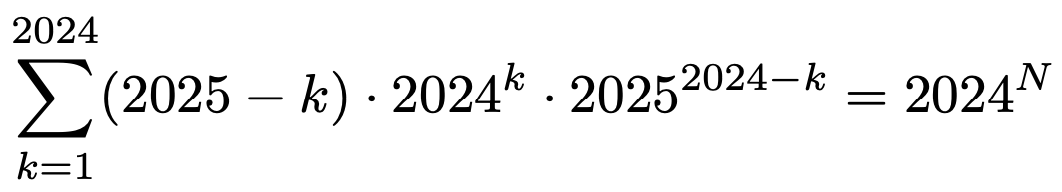
Solution.

4. 372024의 십의 자리 숫자, 일의 자리 숫자를 각각 구하여라.
Solution.
100의 오일러 피 함수(Euler phi function)는 다음과 같다.
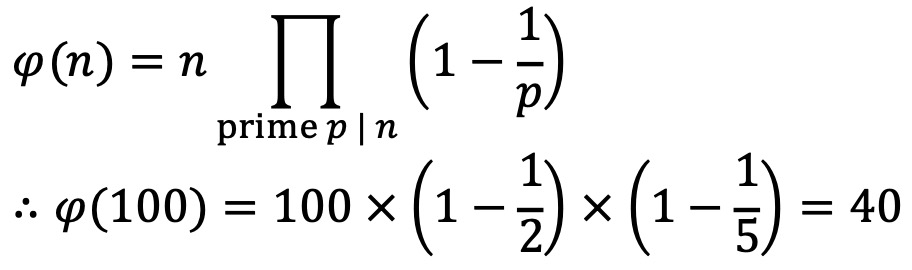
따라서, 37과 100은 서로 소이므로 오일러 정리에 의해 다음이 성립한다.
37φ(100) ≡ 3740 ≡ 1 (mod 100)
그러므로 다음이 성립한다.
372024 ≡ 3724 = (30 + 7)24
372024 ≡ 24 × 30 × 723 + 724
372024 ≡ 20 × (74)5 × 73 + (74)6
372024 ≡ 20 × 343 + 1
372024 ≡ 61 (mod 100)
5. 실수 전체에서 정의된 실함수 f(x)는 두 번 미분가능하고 f''(x)가 연속이다. 그리고 모든 x에 대하여 f'(x) > 0이고 f''(x) < 0이다. 이때 임의의 양수 t에 대하여 다음이 성립함을 증명하여라.
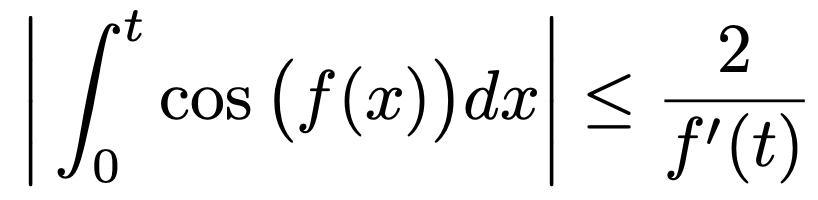
Solution.
공식 풀이를 참고하였다.
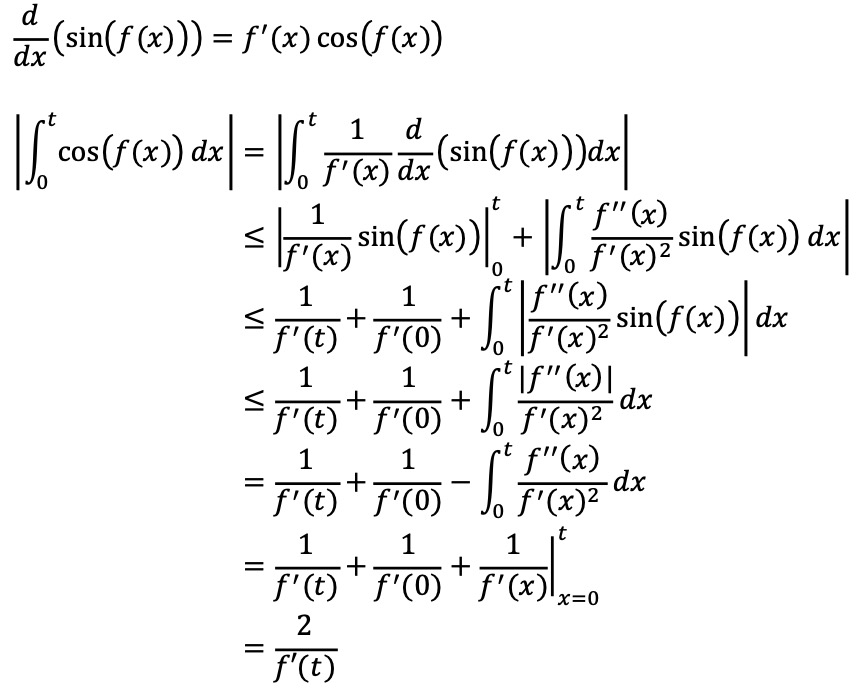
6. 아래 두 조건을 만족하는 n개의 실수 a1, a2, ···, an에 대하여 다음의 최댓값을 구하여라. (단, n ≥ 3)
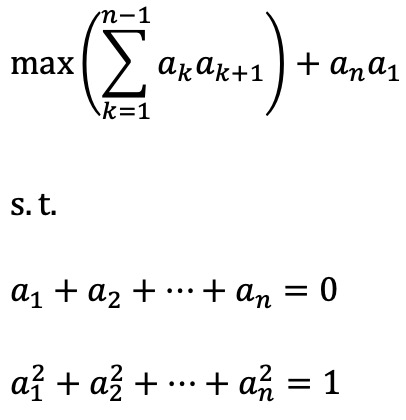
Solution. (저의 풀이)
맨 처음에는 이차형식 행렬 A에 대하여 다음 풀이를 시도했으나, a1 + a2 + ··· + an = 0 조건 때문에 더 진행하기는 어려웠다.
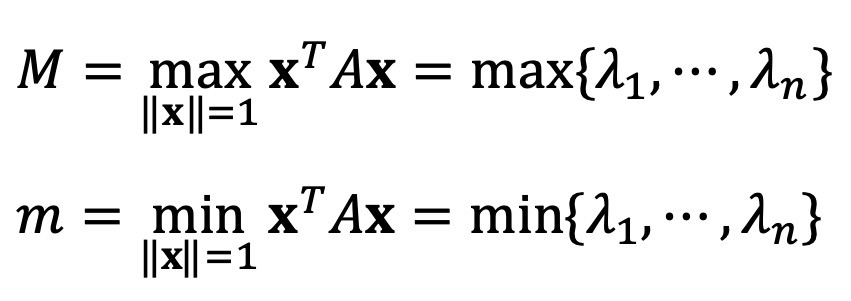
하지만, 정식 풀이를 보면 선형대수학과 관련 있음은 분명하다.
목적함수 및 제약함수가 모든 (a1, ···, an)에서 미분 가능하므로 목적함수의 최댓값은 극대값에서 결정된다.
여러 개의 등식 제약 하 라그랑주 승수법(Lagrange multiplier)을 이용하여 극대값을 찾아보자.
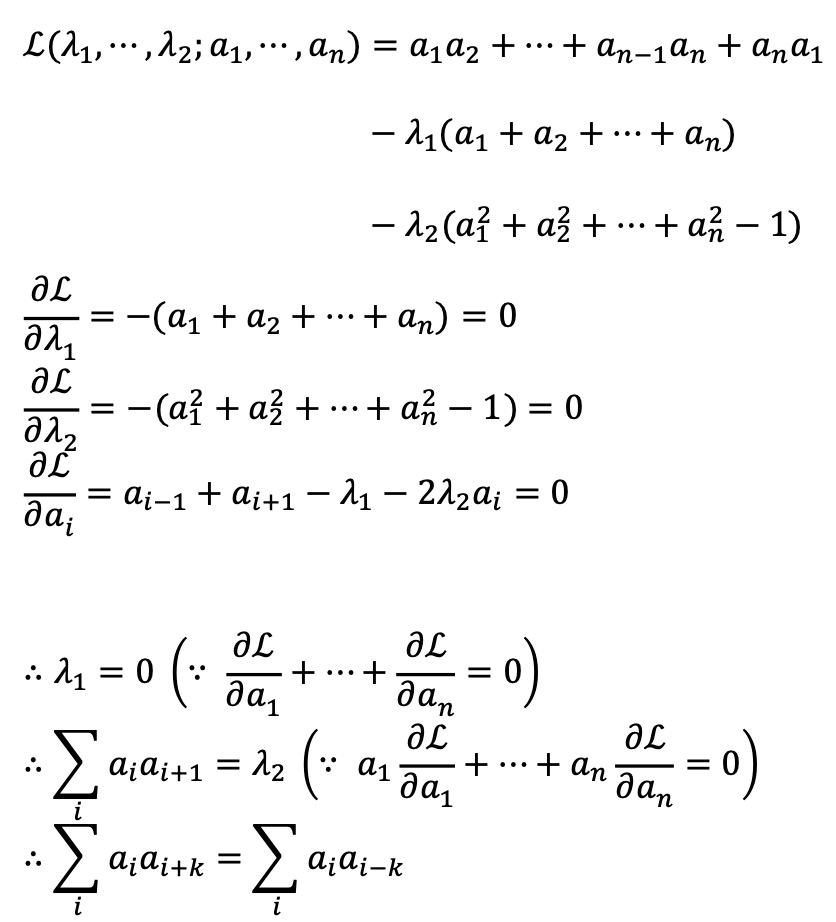
이제 군이론(group theory)에서 아이디어를 채용하여 ∑ 연산 하에서 순환적 특성을 갖는 f(a, b) = ∑i ai+aai+b의 특징을 파악하자.
○ f(0, 0) = 1
○ f(a, b) = f(b, a) : 교환 법칙
○ f(a+c, b+c) = f(a, b)
○ f(a+c, b) = f(a-c, b)
○ f(a, b+c) = f(a, b-c)
○ ∑c f(a+c, b) = 0 (∵ (a1 + a2 + ··· + an)2 = 0)
○ ∑c f(a, b+c) = 0 (∵ (a1 + a2 + ··· + an)2 = 0)
n × n 행렬의 (a, b)에 f(a, b) 값을 표시하면 우향하는 대각선 방향으로 1이고, 그 대각선을 기준으로 + 모양으로 값이 대칭적으로 나타난다.
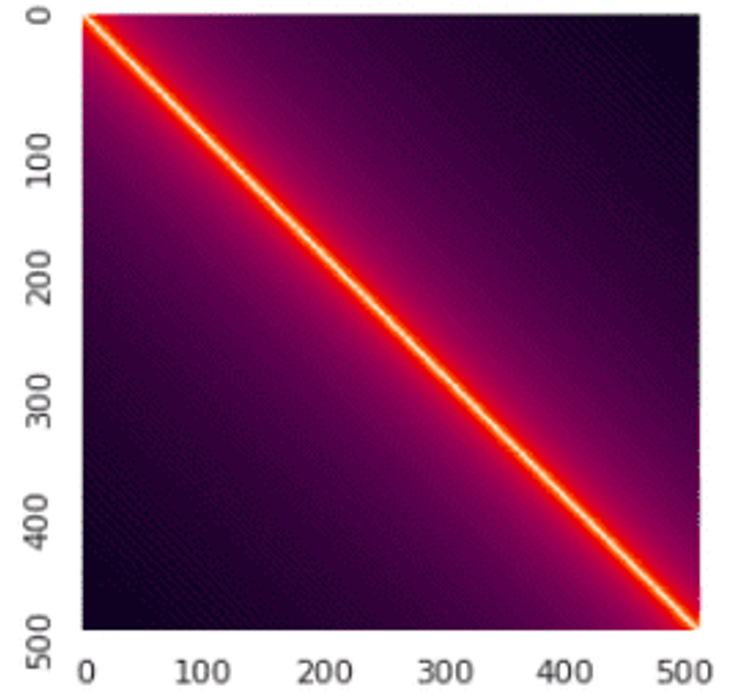
더욱이 임의의 행 혹은 열을 골라 그 함숫값들을 모두 더하면 0이 되므로 f는 cyclic 하다고 추정할 수 있다.
따라서 cyclic 함수 g에 대하여 f(a, a ± c) = g(2πc/n), g(0) = 1로 둘 수 있다.
표현 이론(representation theory)에 따르면, 유한 순환군(아벨군)의 실 1차원 표현은 궁극적으로 cos나 sin 형태로 표현될 수밖에 없다.
즉, 순환군의 모든 원소는 어떤 고정된 원소의 거듭제곱으로 나타내어지고, 복소함수까지 고려하면 exp(iθ)가 그 원소가 된다.
따라서 g(0) = 1을 고려하면, f(a, a ± c) = cos(2πc/n)이다.
표현 이론을 사용하지 않더라도 비슷한 결론을 낼 수 있다.
임의의 함수 f가 주어져 있어도 f(a, a ± c) = cos(2πc/n)과 유사한 값으로 근사할 수 있다.
그런데 f(a, a) = 1, f(a, a+1) ≃ cos(2π/n) ···, f(a, a+(n-1)) ≃ cos(2(n-1)π/n)을 만족하기 위해 (a1, ···, an)을 결정해야 한다.
식이 n개이고 변수가 n개이므로 해는 유일하게 결정되고, 앞에서 찾은 f(a, a ± c) = cos(2πc / n)가 바로 그 해이다.
따라서 (준식) ≤ f(a, a+1) = cos(2π/n)이고, 등호조건은 다음과 같다.
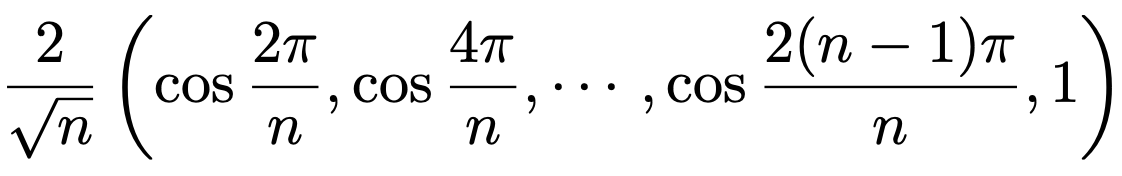
참고로, a1 = 1/√2, a2 = -1/√2, a3 = ··· = an = 0인 경우, 주어진 조건을 만족하지만 라그랑주 승수법 조건을 만족하지 못해 최댓값이 아니다.
Solution. (공식 풀이)
V = ℂn이라 하고 선형사상 ϕ : V → V를 다음과 같이 정의하자.
ϕ(a1, a2, ···, an) = (a2, a3, ···, an, a1)
(n-th root of unity) ζ = e2πi/n = cos(2π / n) + i sin(2π/n)와 1 ≤ k ≤ n에 대하여
vk = (ζk, ζ2k, ···, ζnk)
이라 하자. (예컨대 vn = (1, 1, ···, 1)이다.) 그러면 다음이 성립한다.
○ ϕ(vk) = ζkvk. 즉, vk는 ϕ의 (고유값 ζk에 대한) 고유벡터이다. 특히, 벡터 {v1, v2, ···, vn}은 복소 벡터공간 V = ℂn의 기저를 이룬다.
○ vk · v*k = (ζk, ζ2k, ···, ζnk) · (ζ-k, ζ-2k, ···, ζ-nk) = n (단, v*는 v의 켤레복소수)
○ j := k1 - k2 ≠ 0 ⇒ vk1 · v*k2 = ζj + ζ2j + ··· + ζnj = 0 (단, v*는 v의 켤레복소수)
다음과 같이 문제의 조건을 만족시키는 임의의 벡터 v를 생각하자.
⑴ v = (a1, a2, ···, an) ∈ ℝn
⑵ a1 + a2 + ··· + an = 0
⑶ a12 + a22 + ··· + an2 = 1
벡터 v의 기저 {v1, v2, ···, vn}에 대한 좌표 표현이 다음과 같다고 하자.
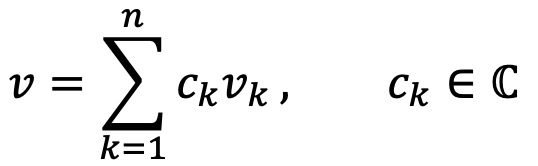
조건 ⑵에 의하여,
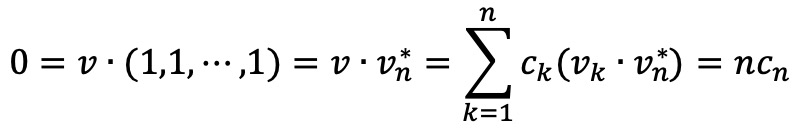
조건 ⑶에 의하여,
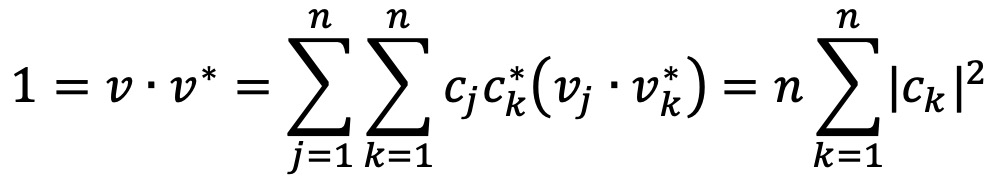
이로부터 다음을 얻을 수 있다.
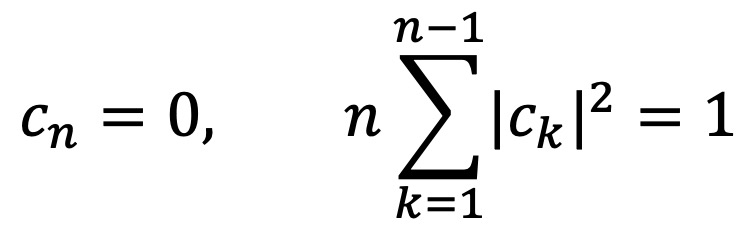
이제,
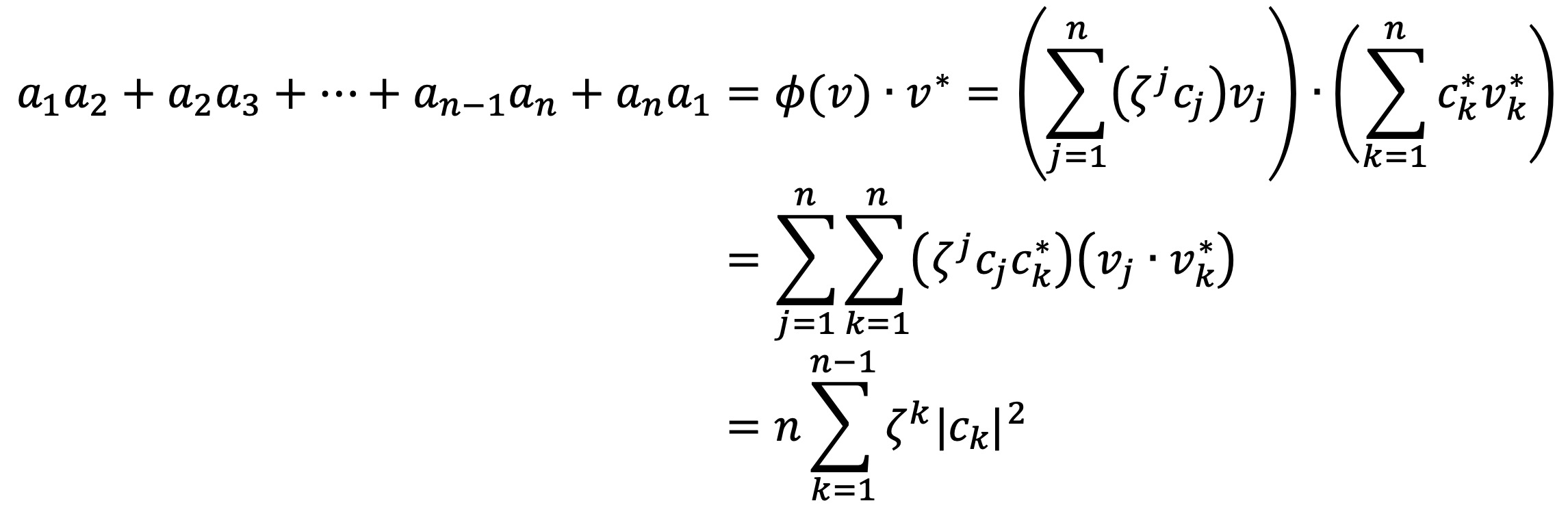
이 값이 실수이므로,
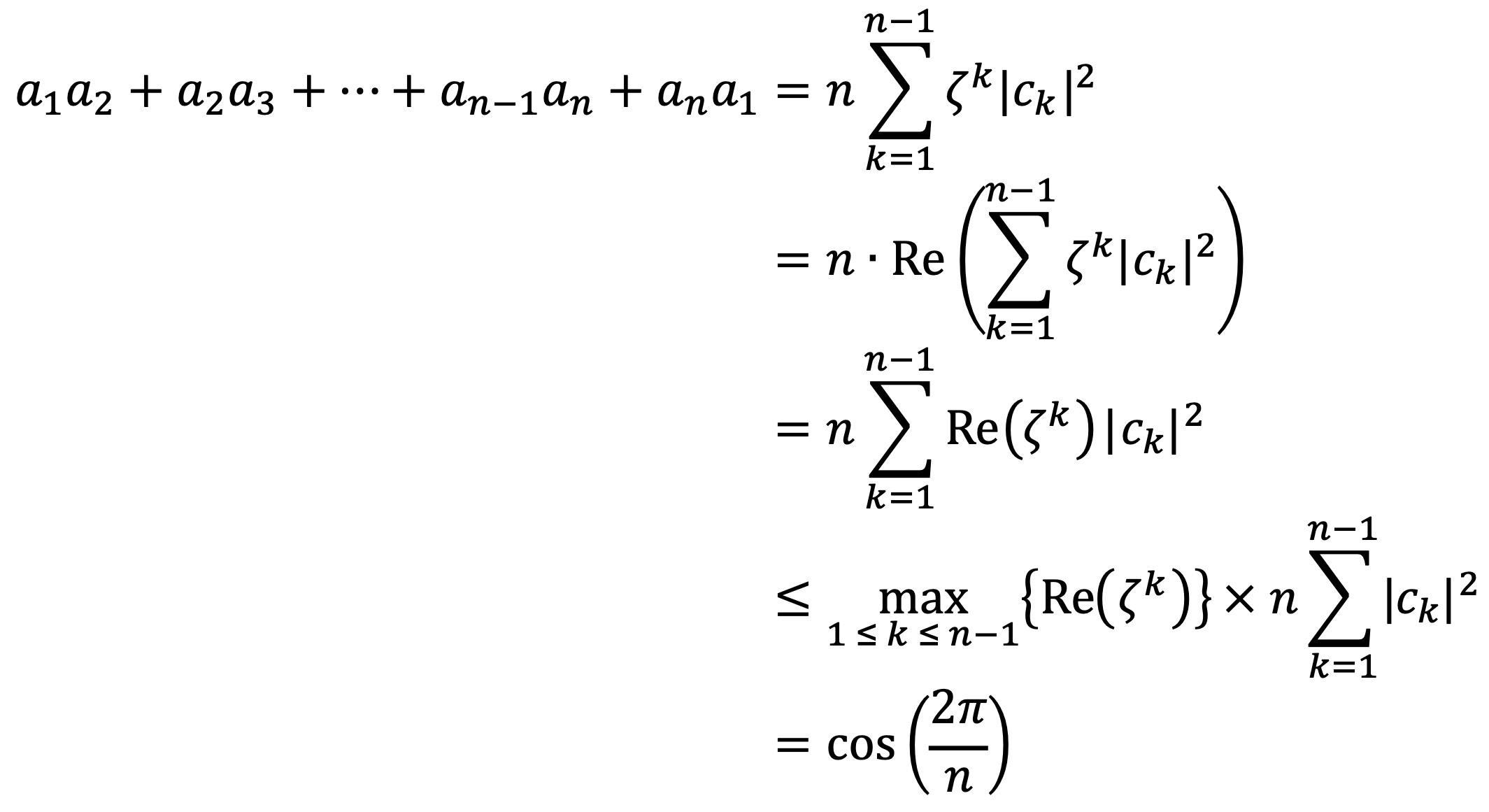
따라서 a1a2 + a2a3 + ··· + an-1an + ana1의 최댓값은 cos(2π/n)이며, 이 값을 갖게 되는 것은
c2 = c3 = ··· = cn-2 = 0
이 되는 경우이므로, v = c1v1 + cn-1vn-1의 꼴이다. 이때
v = c1(ζ, ζ2, ···, ζn) + cn-1(ζ*, ζ*2, ···, ζ*n) ∈ ℝn
이므로 cn-1 = c*1임을 알 수 있다. 또한 n(|c1|2 + |cn-1|2) = 1이므로
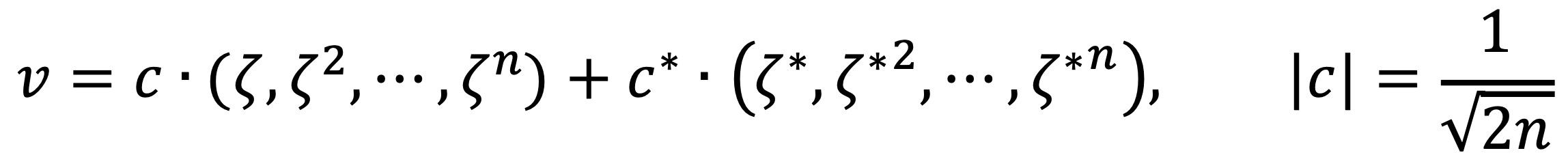
의 꼴임을 알 수 있다. 특히 c = 1 / √(2n)일 때,
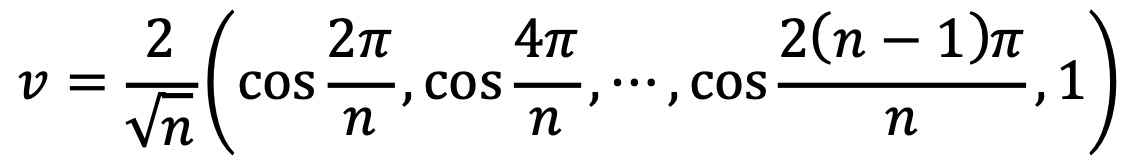
으로 택하면 최댓값 cos(2π / n)를 얻는다.
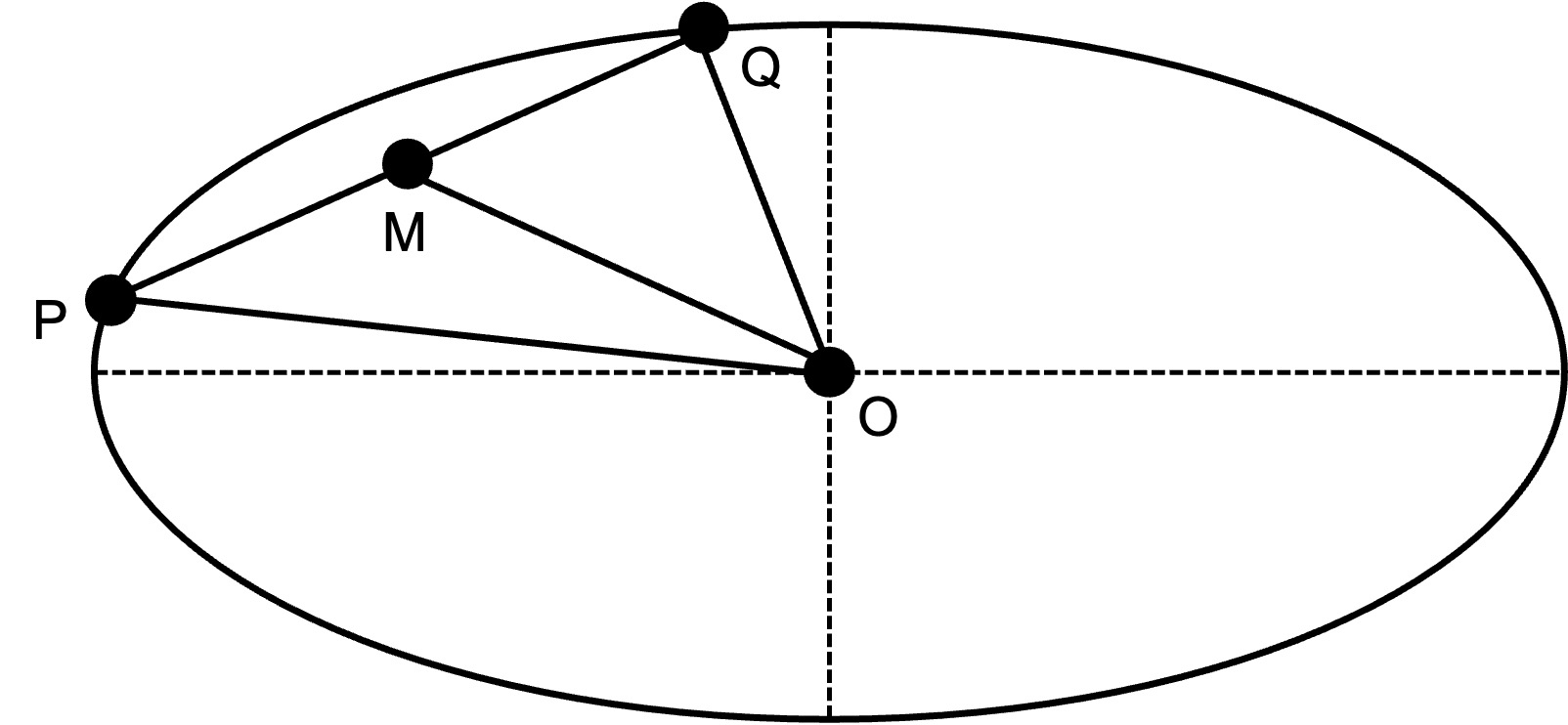
7. 2차원 좌표평면 위의 유한한 닫힌 블록 영역 D에 대하여 D의 경계 β가 다음을 만족한다고 하자.
⑴ β는 매끄러운 단순폐곡선이다.
⑵ β 위의 임의의 점 O에 대하여 O를 중심으로 하는 반지름이 1인 원은 β와 두 점에서만 만난다.
⑶ β 위의 임의의 점 O에서 그린 접선은 O를 제외한 다른 점에서 β와 만나지 않는다.
길이가 1인 막대 PQ의 중점을 M이라 하자. 막대의 양 끝점 P, Q가 항상 β 위에 놓이도록 막대를 한 바퀴 돌리면(즉, 곡선 β를 따라 두 점 P, Q를 연속적으로 한 바퀴 돌리면) M의 자취가 단순폐곡선 γ가 된다고 하자. 이때 두 곡선 β와 γ 사이에 있는 영역의 넓이가 π/4임을 보여라.
Solution.
위와 같은 삼각형이 주어져 있을 때, 파푸스의 중선정리에 따르면 a2 + b2 = 2(c2 + d2)이 성립한다.
그러므로 다음이 성립한다.
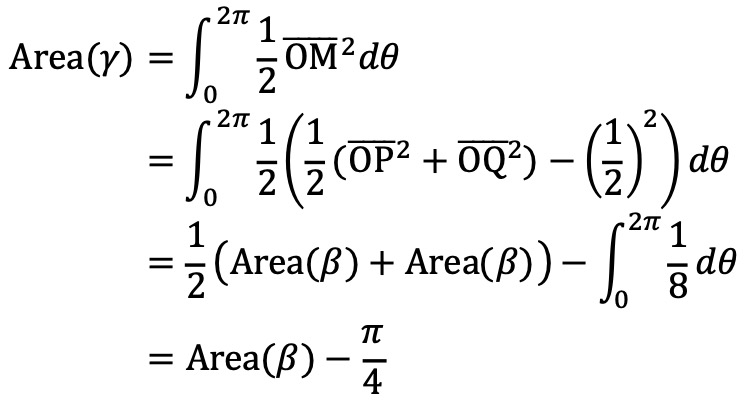
입력: 2024.12.06 19:02