【선형대수학】 1강. 벡터공간
1강. 벡터공간(vector space)
추천글 : 【선형대수학】 선형대수학 목차
1. 행렬의 연산 [본문]
2. 벡터공간 [본문]
1. 행렬의 연산 [목차]
⑴ 행렬의 정의
① m × n 행렬 A, i 번째 행 벡터(row vector), j 번째 열 벡터(column vector)를 다음과 같이 정의

② 영행렬(zero matrix) 또는 널행렬(null matrix) : 모든 원소가 0인 행렬
③ 정사각행렬(square matrix)
⑵ 행렬의 덧셈

⑶ 행렬의 곱셈
① 행렬 X의 i 행, j 열의 원소를 X[i][j]라 하고, A ∈ ℝl×m, B ∈ ℝm×n, C ∈ ℝl×n, C = A × B라고 할 때 다음이 성립

② 성질 1. 일반적으로 AB ≠ BA

③ 성질 2. AB = O라고 해서 A = O 또는 B = O라고 할 수 없음

④ 성질 3. 행렬의 곱셈과 덧셈 사이에 다음 관계가 성립함
○ A(B+C) = AB + AC, (A+B)C = AC + BC
○ A(BC) = (AB)C
○ c(A + B) = cA + cB
⑤ 정리 1. 케일리-해밀턴 정리(Cayley–Hamilton theorem)

○ 이를 응용하여 An = (A2 - (a + d)A + (ad - bc)E) Q(A) + kA + sE와 같이 An (단, n ≥ 2)을 계산할 수 있음
⑥ 프로그래밍 코드
○ 파이썬 numpy 이용
import numpy as np
# 두 행렬 정의
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
# 행렬 출력
print("Matrix A:")
print(A)
print("\nMatrix B:")
print(B)
# 행렬 곱셈
result = np.dot(A, B)
## Alternatively, result = A@B
print("\nNumpy 행렬 곱 결과:")
print(result)
○ 파이썬 sympy 이용
from sympy import Matrix, init_printing
# LaTeX 스타일 출력 초기화
init_printing()
# 두 행렬 정의
A = Matrix([[1, 2], [3, 4]])
B = Matrix([[5, 6], [7, 8]])
# 행렬 출력
print("Matrix A:")
display(A)
print("Matrix B:")
display(B)
# 행렬 곱셈
result = A * B
print("Sympy 행렬 곱 결과:")
display(result)
⑷ 전치행렬(transposed matrix)
① 정의
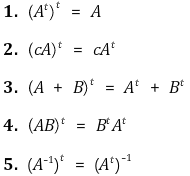
② 대칭행렬(symmetric matrix, sym) : A가 정사각행렬이고 A와 A의 전치행렬이 같은 경우
③ X ∈ ℝN×d (N개의 d차원 데이터)가 주어져 있을 때,
○ XtX ∈ ℝd×d는 μ = 0일 때의 covariance matrix
○ XXt ∈ ℝN×N는 dot matrix (similarity matrix)
④ 성질 1. (At)t = A
⑤ 성질 2. (A + B)t = At + Bt
⑥ 성질 3. (rA)t = rAt
⑦ 성질 4. AB의 전치행렬 (AB)t = BtAt
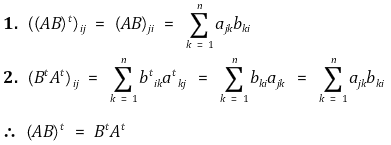
⑧ 성질 5. A, B가 symmetric이고 AB = BA라면 AB는 symmetric
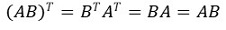
⑸ 대각합 : trace 또는 tr로 표시함
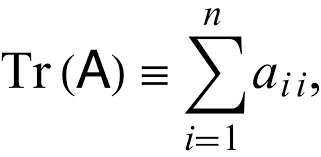
① 성질 1. tr(E) = n, tr(O) = 0
② 성질 2. tr(A + B) = tr(A) + tr(B)
③ 성질 3. tr(cA) = ctr(A), c ∈ ℝ
④ 성질 4. tr(AT) = tr(A)
⑤ 성질 5. tr(AB) = tr(BA)
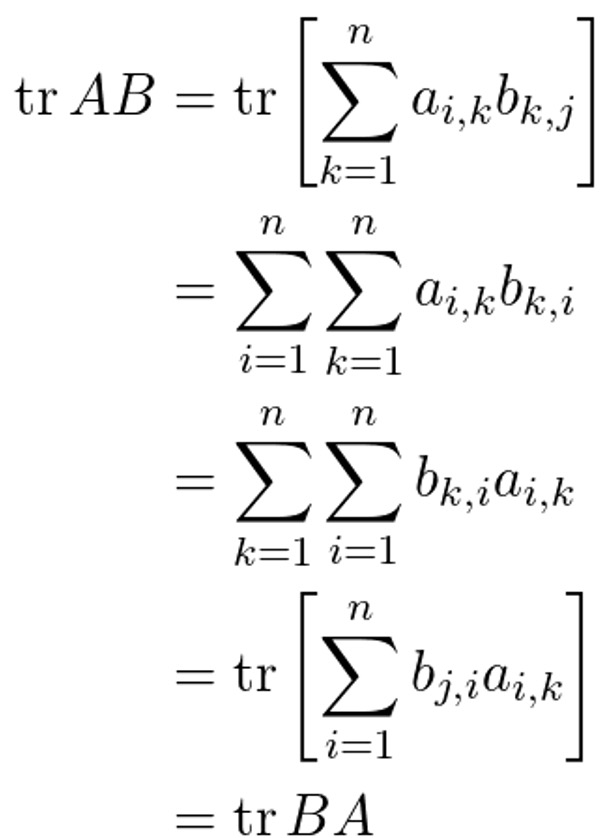
⑥ 성질 6. 일반적으로 tr(AB) ≠ tr(A) × tr(B)
⑦ 성질 7. tr(ATB) = vec(A)·vec(B)
⑧ 성질 8. tr(ABC) = tr(BCA) = tr(CAB) (∵ 결합법칙)
⑨ 성질 9. A, B가 positive semi-definite matrix라면, tr(AB) ≤ tr(A)·tr(B)
⑩ 성질 10. tr(An) = tr(P-1DnP) = tr(P-1PDn) = tr(Dn) = ∑i λin
○ 다만, 위 식은 대각화 가능성과 별개로 성립하는 것처럼 보임
⑹ 가우스 소거법(Gaussian elimination)
① 선형연립방정식
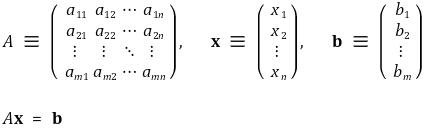
② 확장행렬(augmented matrix) : m × (n + ℓ) 행렬 (A | B)를 지칭
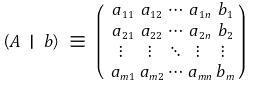
③ 가우스-요르단 소거법(Gauss-Jordan elimination) : 행 단위로 연산
○ 연산 1. 두 행 벡터의 위치를 서로 교환 : 방정식의 순서를 바꿈
○ 연산 2. 특정 행 벡터에 c를 곱함 : 한 방정식의 양변에 c를 곱함
○ 연산 3. 한 행 벡터에 c를 곱하여 다른 행 벡터를 더함 : 한 방정식에 c를 곱하여 다른 방정식에 더함
○ 최종 단계 : 행간소 사다리꼴(reduced row echelon form, RREF)을 만들어야 함

④ 장점 : 프로그래밍으로 구현할 수 있음
2. 벡터공간(vector space) [목차]
⑴ 벡터공간의 조건
① 덧셈에 대한 항등원 : V의 임의의 원소 x에 대하여 x + 0 = x인 0이 V에 존재
② 덧셈에 대한 역원 : x ∈ V이면 x + (-x) = 0인 -x가 V에 존재
③ 덧셈에 대한 교환법칙 : x, y ∈ V이면 x + y = y + x
④ 덧셈에 대한 결합법칙 : x, y, z ∈ V이면 (x + y) + z = x + (y + z)
⑤ 분배법칙 : c(x + y) = cx + cy
⑥ 분배법칙 : (c1 + c2)x = c1x + c2x
⑦ 곱셈에 대한 항등원 : 1x = x
⑧ 곱셈에 대한 결합법칙 : c1(c2x) = (c1c2)x
⑵ 선형사상
① 선형사상(linear transformation) : 사상 T : U → V가 x, y ∈ U, c ∈ F에 대해 다음 조건을 만족하는 경우
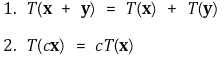
② 선형결합(linear combination)
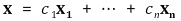
③ 선형종속(linearly dependent)
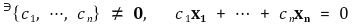
④ 선형독립(linearly independent)
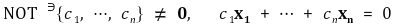
⑤ 생성집합(spanning set) : 벡터공간 V의 임의의 벡터가 S의 원소들의 선형결합으로 표시되는 경우 그 S를 지칭함
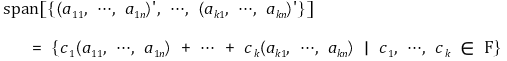
⑥ 기저(basis) : 생성집합 중에서 선형독립인 것
⑶ T의 역사상 T-1 : V → U가 존재하면 T-1도 선형사상
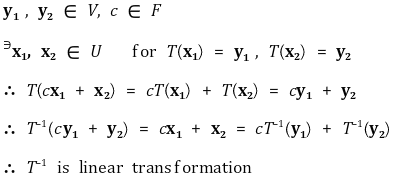
⑷ 내적공간(inner product space)
① 내적(inner product, dot product)의 조건
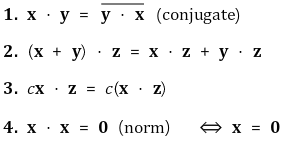
② 표준내적(standard inner product) : V = ℂn에서 표준내적을 다음과 같이 정의
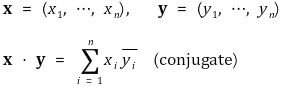
③ 내적의 성질
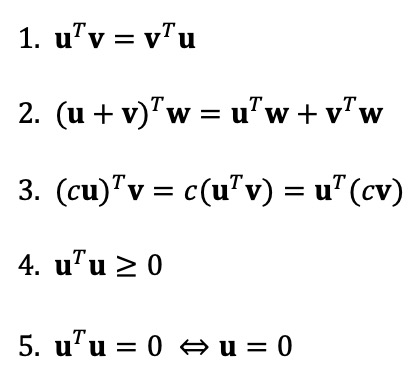
④ 내적공간(inner product space) : 내적이 정의되어 있는 벡터공간
○ 실내적공간 : 스칼라체가 실수 집합인 경우
○ 복소내적공간 : 스칼라체가 복소수 집합인 경우
⑤ 노음(노름, norm)
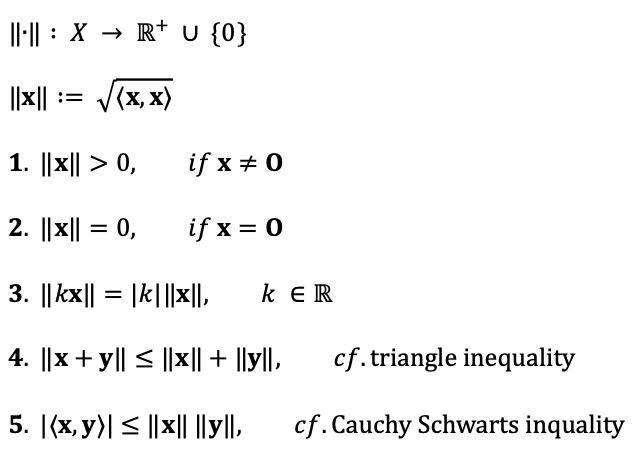
⑥ 정리 1. 코시-슈바르츠 부등식(Cauchy-Schwartz inequality)
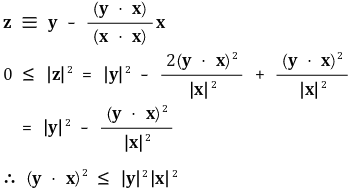
⑦ 정리 2. 삼각부등식(triangular inequality)
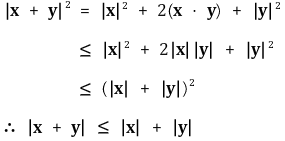
⑷ 거리공간(metric space)
① 거리함수(distance function, metric)
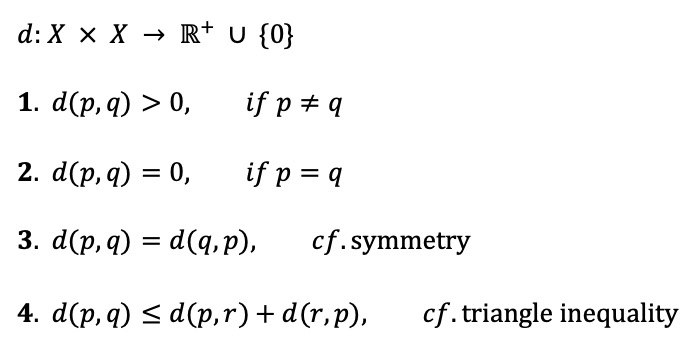
○ 거리함수의 종류
② 노음과 거리(distance)의 관계
○ 노음이 정의되면 거리(distance) d를 정의할 수 있음
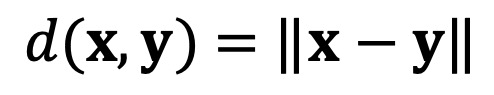
○ 거리가 정의돼 있다고 하여 대응되는 노음이 항상 존재하는 것은 아님
③ 커널(kernel)
○ 비선형사상(non-linear map) φ(x) : X → H를 이용하여 거리 d를 달리 정의할 수도 있음
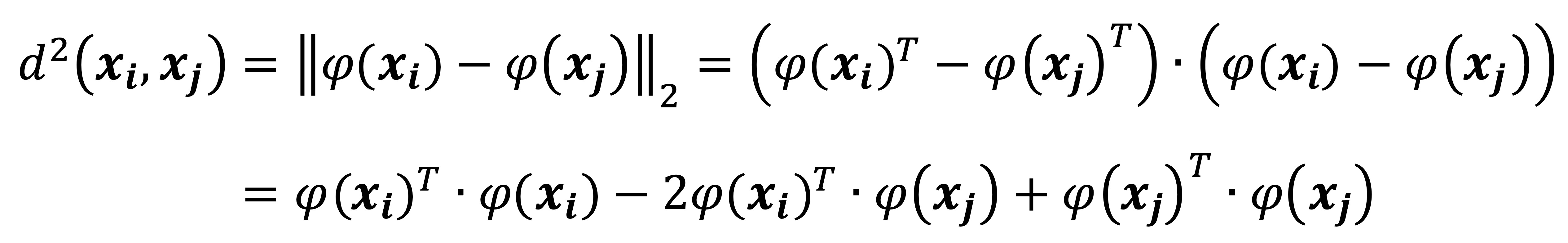
○ 커널의 정의 : k(xi, yi) ≡ φ(xi)Tφ(xj)
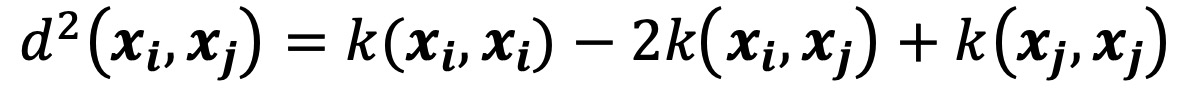
○ 커널의 특징
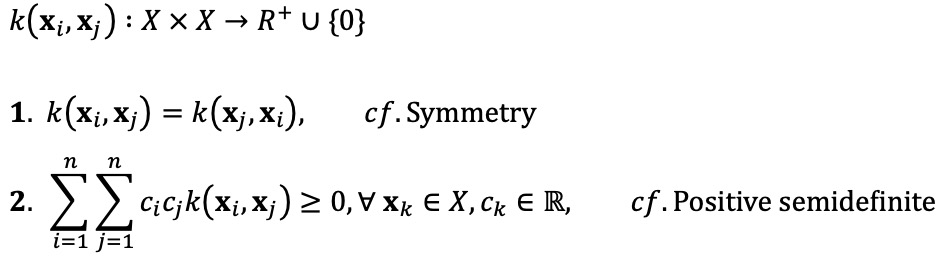
○ 커널 예시
○ φ(x, y) = (x, y, x2 + y2)T
○ k(v, u) = uTv (단, 이 경우 φ(·)는 항등함수)
○ 가우시안 커널(Gaussian kernel) : k(v, u) = exp(-||v - u||2 / 2σ2)
○ 다항 커널(polynomial kernel) : k(v, u) = (uTv + 1)d (단, d는 다항 차수(polynomial degree))
○ 시그모이드 커널(sigmoid kernel) : k(v, u) = tanh(αuTv + β)
○ RBF 커널(radial basis function kernel) : k(v, u) = exp(-γ ||v - u||2)
⑸ 부분공간(subspace) : 생성집합은 부분공간을 span한다
입력: 2020.04.07 21:36
수정: 2024.10.10 08:12
