【선형대수학】 3강. 행렬식과 역행렬
3강. 행렬식과 역행렬
추천글 : 【선형대수학】 선형대수학 목차
1. 행렬식 [본문]
2. 역행렬 [본문]
3. 크래머 공식 [본문]
1. 행렬식(determinant) [목차]
⑴ 치환의 정의
① 치환(순열, permutation) : S = {1, 2, ···, n}의 치환이란 S에서 S로의 일대일 대응 함수 σ를 지칭함
○ 이때 함수를 간단히 (f(1), ···, f(n))으로 씀
○ 항등치환 : (1, 2, ···, n). 즉, f(i) = i인 경우
② 호환 : (f(1), ···, f(i), ···, f(j), ···, f(n))을 (f(1), ···, f(j), ···, f(i), ···, f(n))로 바꾸는 변환
○ 즉, 호환은 치환의 정의역의 두 원소에서 서로의 치역을 맞바꾸는 것
○ (1, ···, n)에서 유한 번의 호환을 곱하면 임의의 치환을 만들 수 있음
③ 치환의 부호
○ 홀치환(기치환, odd permutation) : 홀수 개의 치환의 곱으로 항등치환을 만들 수 있는 치환
○ 짝치환(우치환, even permutation) : 짝수 개의 치환의 곱으로 항등치환을 만들 수 있는 치환
○ 치환 σ가 기치환인 경우 sgn(σ) = -1, 우치환인 경우 sgn(σ) = +1로 정의함
④ 대칭군의 기우성 : 짝치환이면서 홀치환일 수는 없음
○ 우선 f(0) = 0이라고 가정
○ 반전
○ α ≤ x ≤ β, f(x) > f(y)인 x의 개수를 M(k)α, β 혹은 반전이라고 정의
○ 반전의 합

○ 정의
○ n1 : f(n) > f(a)이고 0 < n < i인 n의 개수
○ n2 : f(a) > f(n) > f(b)이고 0 < n < i인 n의 개수
○ n3 : f(b) > f(n)이고 0 < n < i인 n의 개수
○ n4 : f(n) > f(a)이고 i < n < j인 n의 개수
○ n5 : f(a) > f(n) > f(b)이고 i < n < j인 n의 개수
○ n6 : f(b) > f(n)이고 0 < n < i인 n의 개수
○ 상황 1. f(i) = a, f(j) = b인 경우 (단, f(a) > f(b)라고 가정)

Figure. 1. 치환의 첫 번째 상황

○ 상황 2. f(i) = b, f(j) = a인 경우 (단, f(a) > f(b)라고 가정)

Figure. 2. 치환의 두 번째 상황

○ 결론 : 치환은 기우성이 있음

⑵ 행렬식의 정의 : [A]j를 행렬 A의 j번재 열 벡터라 할 때,
① 성질 1. det[I] = 1
② 성질 2. 치환의 부호와 관련된 성질
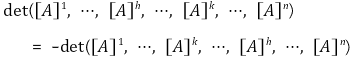
○ 2-1. A = ([A]1, ···, [A]n)에서 [A]h = [A]k (1 ≤ h ≠ k ≤ n)이면 det(A) = 0
③ 성질 3. det(A) = det([A]1, ···, [A]n)은 각 열 벡터들에 관한 다중선형함수
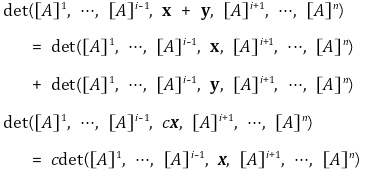
○ 3-1. A = ([A]1, ···, [A]n)에서 [A]i = 0이면 det(A) = 0 (∵ 0 + 0 = 0)
○ 3-2. 열에 대한 유용한 연산 : 전치행렬에서도 행렬식이 같으므로 행에 대한 연산도 허용됨
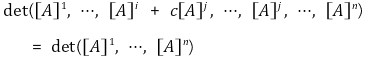
④ 성질 1, 성질 2, 성질 3을 만족하는 유일한 함수는 다음과 같음

⑶ 행렬식의 계산
① 2 × 2 행렬의 행렬식
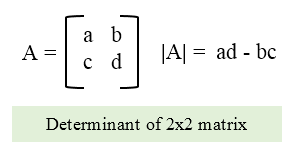
② 3 × 3 행렬의 행렬식
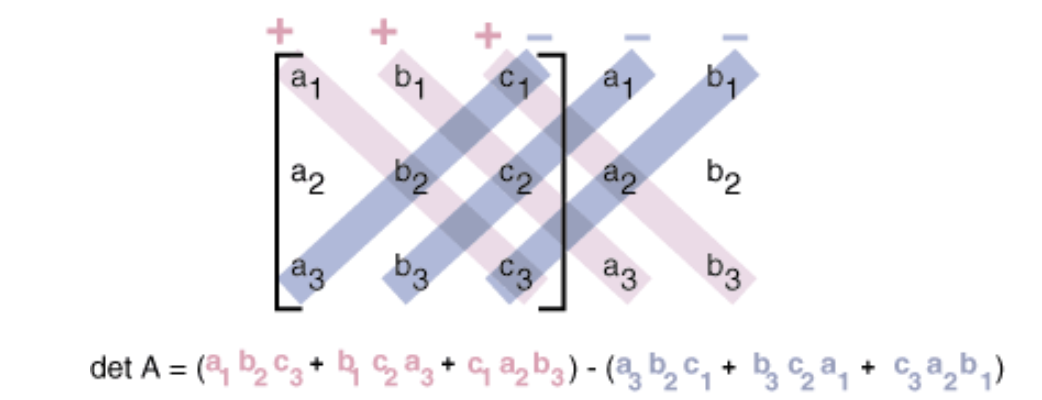
③ 여인수 전개(cofactor expansion) : 소행렬식을 이용한 행렬식 계산
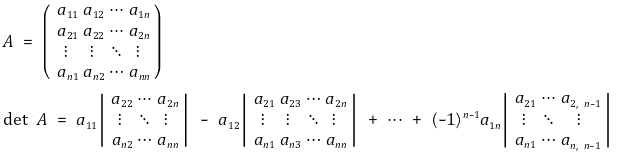
⑷ 행렬식의 응용
① 정리 1. n × n 행렬 A의 계수가 n보다 작으면 det(A) = 0임
○ 이유 : 행렬식은 역행렬과 관련하여 유일근의 존재성을 암시하므로
② 정리 2. 전치행렬의 행렬식 : A가 n × n 행렬이면 det(At) = det(A)
③ 정리 3. A, B가 n × n 행렬이면 det(AB) = det(A)det(B)
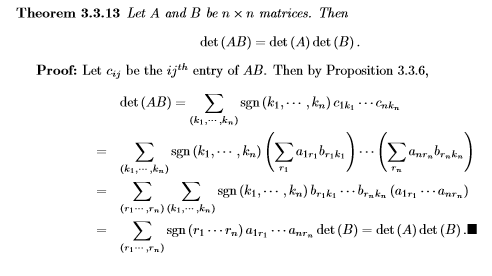
④ 정리 4. X ∈ ℳn, A ∈ ℳr, D ∈ ℳn-r, B ∈ ℳr, n-r에 대해 다음이 성립함

○ 정리 4-1.
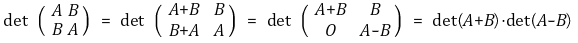
○ 정리 4-2. n × n 행렬 A, B, C, D가 있을 때, |D| ≠ 0이고 CD = DC인 경우
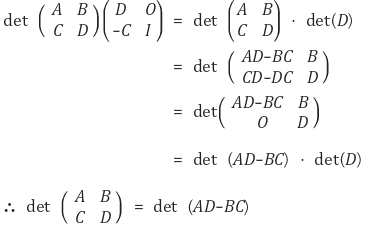
○ 정리 4-3. A ∈ ℳr, B ∈ ℳr, n-r, C ∈ ℳn-r, r, D ∈ ℳn-r에 대하여 다음 등식이 성립함
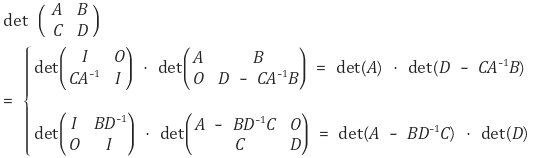
⑤ 정리 5. x와 y가 모두 n차원 열벡터일 때 다음 등식이 성립함
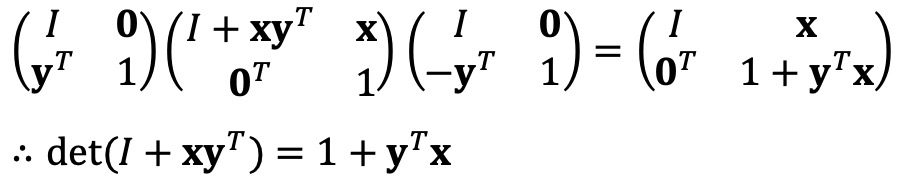
⑥ 정리 6. Vandermonde 행렬식 : 다음이 성립함
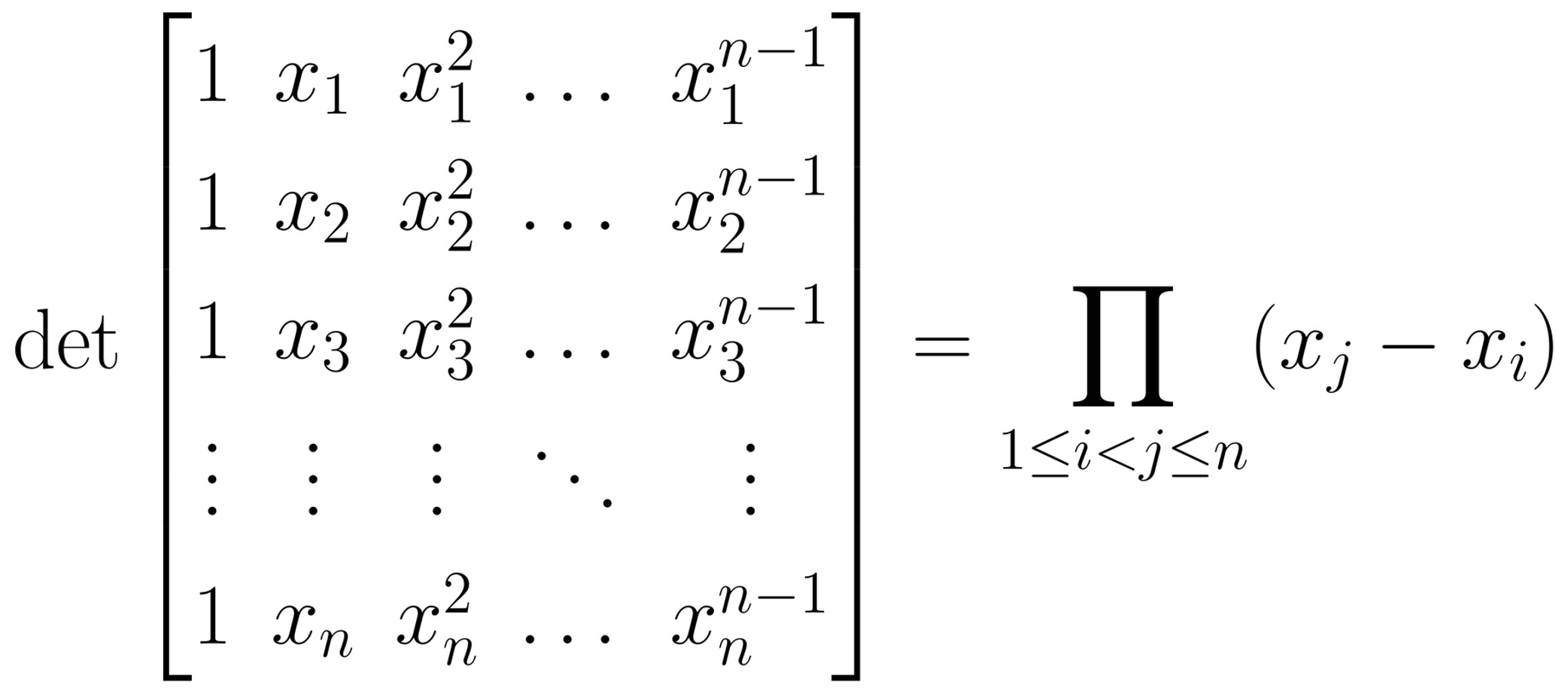
○ 증명
○ 주어진 행렬식은 다항식으로 표현됨 : 예를 들어, xn을 보면 그 다항식은 xn에 대하여 n-1차 이하 다항식
○ 특정 행벡터에서 다른 행벡터를 빼도 행렬식이 바뀌지 않는다는 사실을 주목
○ n번째 행과 1번째 행의 차에서 행렬식이 (xn - x1)을 인수로 가짐을 알고, 비슷하게 (xn - x2), ···, (xn - xn-1)을 인수로 가짐
○ 그러므로 그 다항식은 xn에 대하여 (xn - x1) ··· (xn - xn-1)와 같이 표현됨 : xnn-1이 포함된 항의 계수가 1임을 확인
○ 일반화를 잃지 않고 xn-1, xn-2, ···, x1에 대하여도 비슷하게 표현됨을 알 수 있어 (준식)을 증명함
⑸ 행렬식의 용도
① 용도 1. 행렬식은 선형 변환에 의해 변형된 면적, 부피 등을 의미함
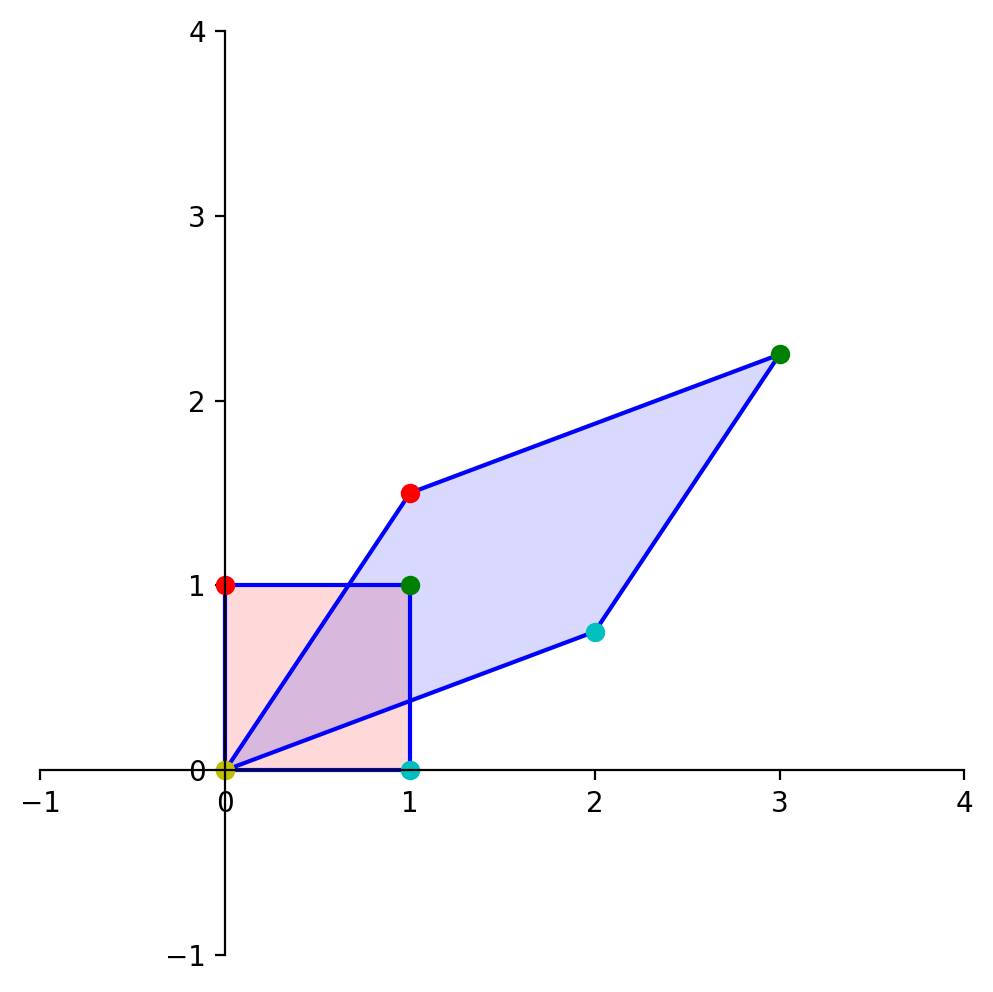
Figure. 3. 2차원 선형변환의 행렬식과 넓이
② 용도 2. 주어진 행벡터 또는 역벡터들이 종속이면 행렬식이 0이고, 독립이면 행렬식이 0이 아님 (그 역도 성립)
○ 경우 1. 종속인 경우 : 행렬식의 성질 2에 의해 행렬식이 0이 됨
○ 경우 2. 독립인 경우
○ 가우스 소거법을 써서 역삼각행렬을 만들더라도 대각성분 중에 0인 게 나올 일이 없음
○ 그러한 역삼각행렬은 행렬식이 0이 아님이 자명
○ 가우스 소거법을 쓰는 과정에서 행렬식이 바뀌지 않음
○ 그러므로 주어진 행벡터 또는 역벡터들이 독립인 행렬은 행렬식이 0이 아님
③ 용도 3. 역행렬의 존재성 : 행렬식이 0인 것과 역행렬이 존재하지 않는 것은 필요충분조건
○ 행렬식 값이 변하지 않는 가우스 소거법으로 역행렬을 자동으로 찾아낼 수 있으므로
④ 용도 4. x-y 평면에서 (x1, y1)', (x2, y2)'를 지나는 직선의 방정식
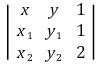
⑤ 용도 5. v = (v1, v2, v3)와 w = (w1, w2, w3)의 외적(cross product)
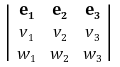
⑥ 용도 6. 론스키 행렬(Wronskian matrix)
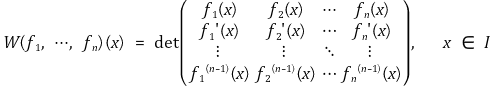
⑦ 용도 7. 야코비 행렬(Jacobian matrix)
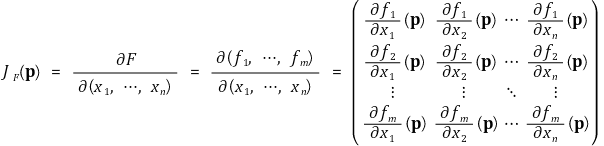
⑧ 용도 8. 헤세 행렬(Hessian matrix)
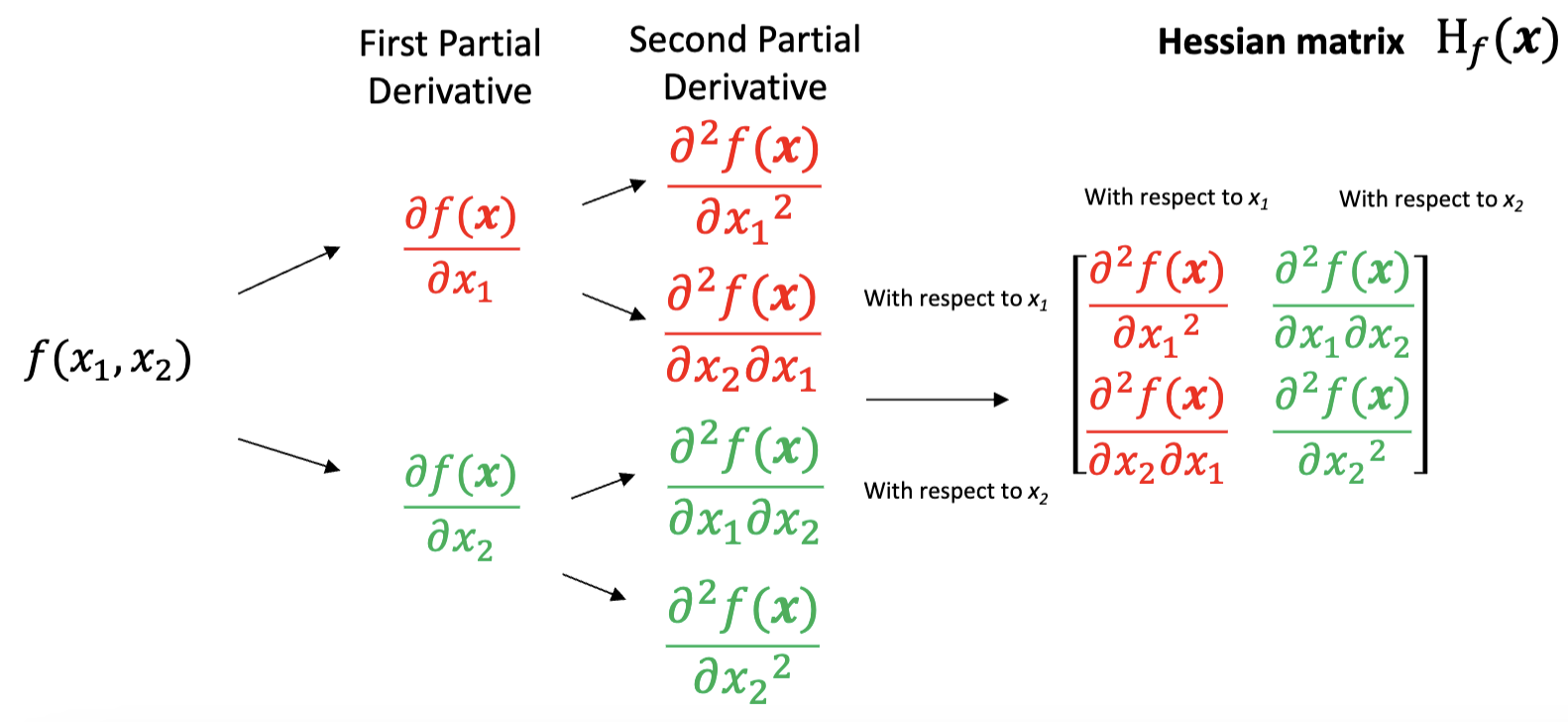
○ 2 × 2 행렬의 헤세 행렬
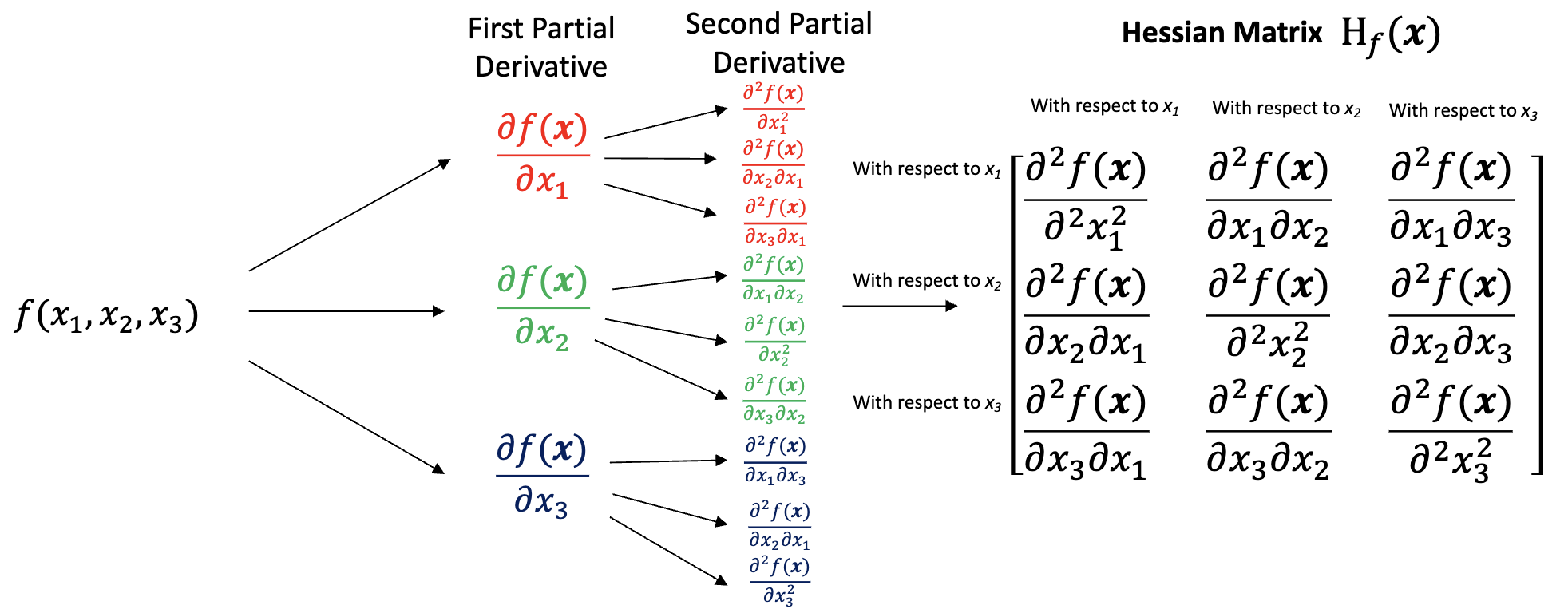
○ 3 ×3 행렬의 헤세 행렬
○ n × n 행렬의 헤세 행렬
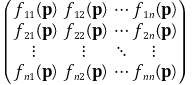
⑨ 용도 9. ► 휘켈 근사와 해밀토니안 (ref)
⑩ 용도 10. 회전 및 반사 변환
○ 회전 변환 : T: x → y를 나타내는 행렬 R이 RTR = RRT = I (등거리), det(R) = 1인 경우
○ 반사 변환 : T: x → y를 나타내는 행렬 R이 RTR = RRT = I (등거리), det(R) = -1인 경우
2. 역행렬(inverse matrix) [목차]
⑴ 정의
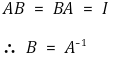
⑵ 가역행렬(invertible matrix) : 역행렬이 존재하는 행렬
① 정리 1. A의 역행렬이 존재하면 그것은 유일함
② 정리 2. A가 가역행렬이면 A-1도 가역행렬임
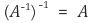
③ 정리 3. A, B가 가역행렬이면 AB도 가역행렬임
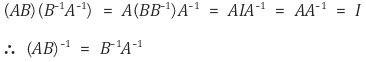
④ 정리 4. A가 가역행렬이면 cA도 가역행렬임
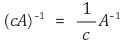
⑤ 정리 5. 역행렬과 전치행렬

⑥ 정리 6. det (Ak) ≠ 0 (단, A는 3 × 3 행렬)인 자연수 k가 존재하면 A는 가역행렬
⑦ 정리 7. (I - Ak) = O (단, A는 3 × 3 행렬이고 I는 단위행렬)인 자연수 k가 존재하면 A는 가역행렬
⑧ 정리 8. Av1 ∪ Av2 ∪ ··· ∪ Avk = ℝ3인 v1, v2, ···, vk가 존재하면 A는 가역행렬
○ 이유 : rank (A) = 3이라는 의미이므로
⑨ Avi ≠ O인 세 개의 직교벡터 v1, v2, v3가 있다는 사정만으로 A를 가역행렬로 볼 수 없음
○ 이유 : A에 의한 사상이 0이 아닌 하나의 벡터로만 가는 경우도 있기 때문
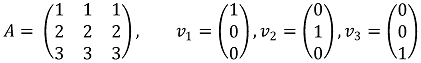
⑶ 역행렬의 계산 1. 삼각행렬로 변형하여 역행렬 구하기
① 행에 관한 기본 연산 : 역행렬을 구할 수 있는 알고리즘을 제공
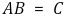
○ ⓐ A의 i 행 행벡터와 j 행 행벡터의 위치를 교환하는 기본연산은 C의 i 행과 j 행의 순서를 바꾼 것과 동일
○ ⓑ A의 i 행 행벡터에 c를 곱하는 기본연산은 C의 i 행에 c를 곱한 행렬과 같음
○ ⓒ A의 j 행 행벡터에 c를 곱하여 다른 i 행 행벡터에 더하는 기본연산은 C에 그러한 연산을 한 것과 동일
② 기본행렬(elementary matrix) : 단 한 번의 행에 관한 기본 연산을 한 것과 같은 효과를 주는 행렬
○ 1형 기본행렬(type 1 elementary matrix) : 첫 번째 기본연산(ⓐ)을 표현하는 행렬
○ 2형 기본행렬(type 2 elementary matrix) : 두 번째 기본연산(ⓑ)을 표현하는 행렬
○ 3형 기본행렬(type 3 elementary matrix) : 세 번째 기본연산(ⓒ)을 표현하는 행렬
③ 정리 1. 기본행렬들은 모두 가역행렬임
○ 1형 기본행렬의 역행렬은 자기 자신
○ 2형 기본행렬의 역행렬
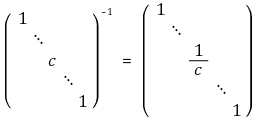
○ 3형 기본행렬의 역행렬
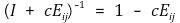
④ 정리 2. 모든 가역행렬은 기본행렬들의 곱으로 표시됨
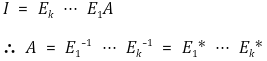
⑤ 정리 3. 모든 삼각행렬은 역행렬이 존재함
○ 삼각행렬(triangular matrix) : 상삼각행렬(upper triangular matrix)이거나 하삼각행렬(lower triangular matrix)인 경우
○ n × n 삼각행렬 A는 기본행렬들의 곱으로 표현할 수 있음
○ 우선 주어진 삼각행렬이 상삼각행렬이라고 가정
○ 1단계. 단위행렬로부터 2행에 a12를 곱한 뒤 1행에 더함
○ 2단계. 1단계 이후 3행에 a13를 곱한 뒤 1행에 더하고, a23를 곱한 뒤 2행에 더함
○ 3단계. 2단계 이후 4행에 a14를 곱한 뒤 1행에 더하고, a24를 곱한 뒤 2행에 더하고, a34를 곱한 뒤 3행에 더함
○ 4단계. 위와 같은 방법으로 주어진 상삼각행렬을 단위행렬로만 표현할 수 있음
○ 하삼각행렬도 동일한 과정을 거칠 수 있음
○ 그러므로 삼각행렬은 역행렬이 존재하고 그 형태를 특정할 수 있음
⑷ 역행렬의 계산 2. 수반행렬(adjoint matrix)
① A가 n × n 행렬일 때 A에서 i행과 j열을 없애고 나면 (n-1) × (n-1) 행렬을 얻음
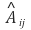
② aij의 여인수(cofactor)
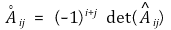
③ 라플라스 전개(Laplace expansion)
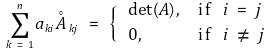
④ 수반행렬
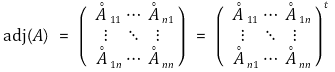
⑤ 역행렬의 계산
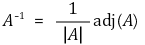
⑸ 역행렬의 계산 3. 프로그래밍 코드
① 파이썬 numpy 이용
import numpy as np
# 예시 행렬 A를 정의합니다.
A = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
# numpy.linalg.inv 함수를 이용해 역행렬을 구합니다.
try:
A_inv = np.linalg.inv(A)
print("A_inv (NumPy):")
print(A_inv)
except np.linalg.LinAlgError:
print("이 행렬은 역행렬이 존재하지 않습니다.")
② 파이썬 sympy 이용
import sympy
# 예시 행렬 A를 정의합니다.
A_sym = sympy.Matrix([
[1, 2, 1],
[0, 1, 2],
[1, 2, 3]
])
# 행렬의 역행렬을 구합니다.
try:
A_sym_inv = A_sym.inv() # .inv() 메서드 사용
print("A_inv (Sympy):")
print(A_sym_inv)
except:
print("이 행렬은 역행렬이 존재하지 않습니다.")
3. 크래머 공식(Cramer's rule) [목차]
⑴ A를 n × n 행렬, x = (x1, ···, xn)', b = (b1, ···, bn)'라 할 때, 연립방정식 Ax = b의 유일해 x0의 j번째 원소는 다음과 같음
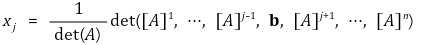
⑵ 증명
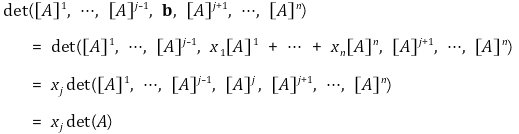
입력: 2020.04.22 09:51
수정: 2024.01.01 18:37
