【대수경】 제 37회 전국 대학생 수학 경시대회 제 1 분야
제 37회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 37회 전국 대학생 수학경시대회
제 1 분야
2018년 11월 17일 (10:00 - 13:00)
1. 벡터 u = (1/3, 1/3, 1/3) ∈ ℝ3에 대하여

로 정의할 때, 급수 ∑n=1 to ∞ (3, 2, 1)·v2n의 값을 구하여라.
Solution.
v2n의 일반항을 다음과 같이 찾을 수 있다.

따라서 (준식)은 다음과 같다.

2. 양의 정수 n에 대하여 n × n 실행렬 A는 tr(A) = 2018을 만족한다. 이때, rank(A) = 1이면 A2 = 2018A임을 보여라.
Solution.
특수한 경우에서 케일리-해밀턴 정리(Cayley-Hamilton theorem)를 증명하는 것과 같다.
rank가 1이라는 것은 A = uvT (단, u ∈ ℝn×1, v ∈ ℝn×1)와 같이 표현될 수 있음을 의미한다.
tr(AB) = tr(BA)가 성립함을 주목하자.
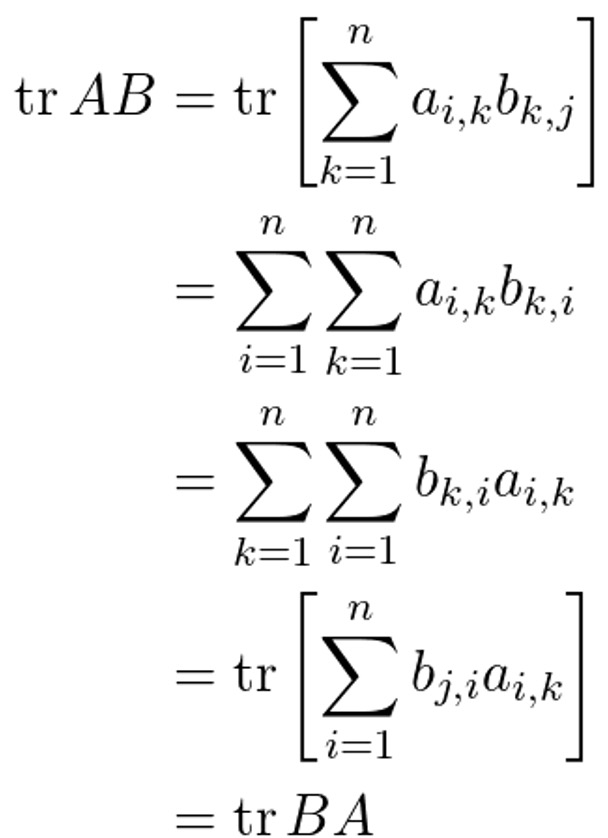
따라서, 2018 = tr(A) = tr(u × vT) = tr(vT × u) = vTu (∵ vTu ∈ ℝ)
그러므로 A2 = uvT × uvT = u × (vTu) × vT = 2018 u × vT = 2018A
3. 좌표평면 ℝ2 상의 영역 S에 대하여 다음 적분이 잘 정의된다고 하자.
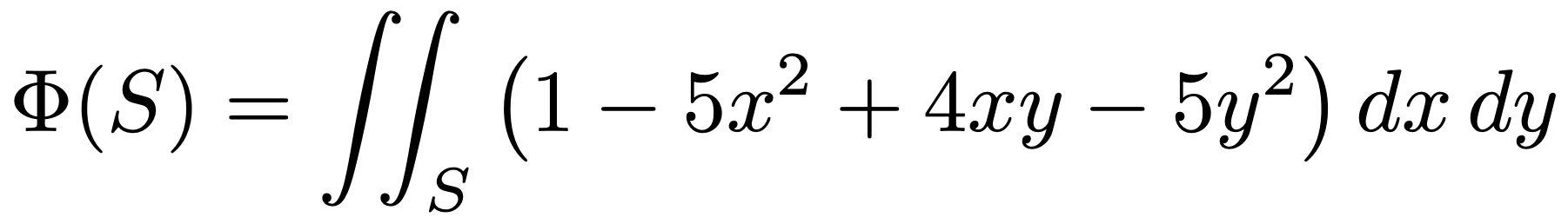
이때, Φ(S)가 취할 수 있는 값의 최댓값을 구하여라.
Solution.
(x', y')을 원점에 대하여 반시계 방향을 θ만큼 회전했을 때 (x, y)라고 하자. 그러면, 다음 식을 얻을 수 있다.
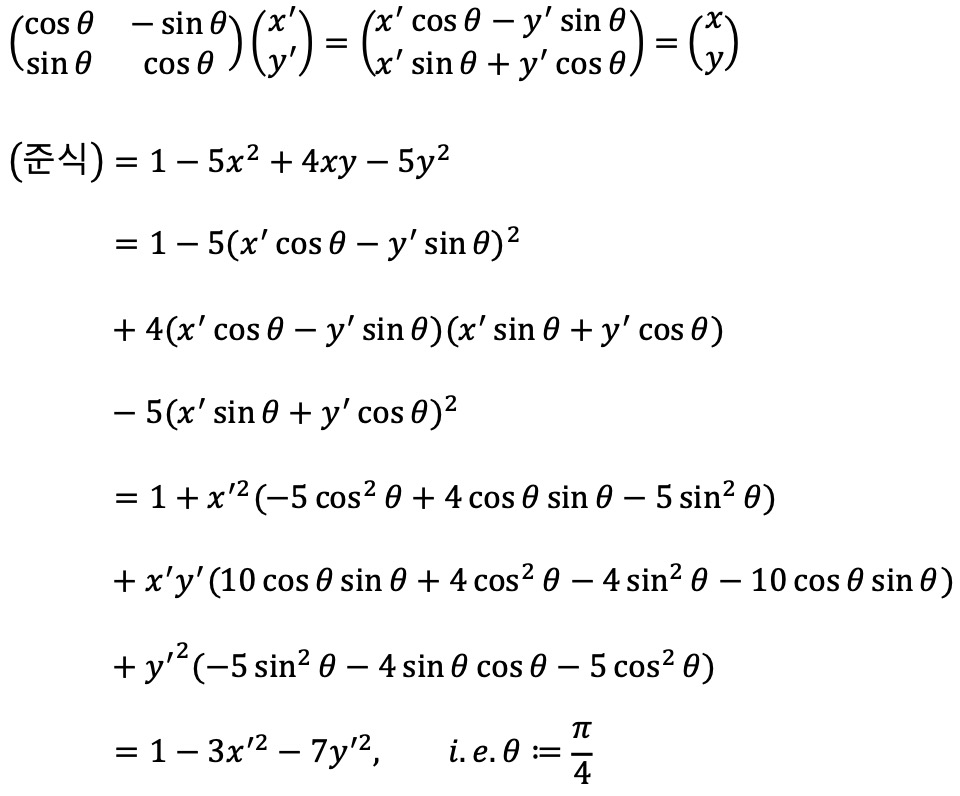
그러므로 Φ(S)의 최댓값은 다음과 같다.
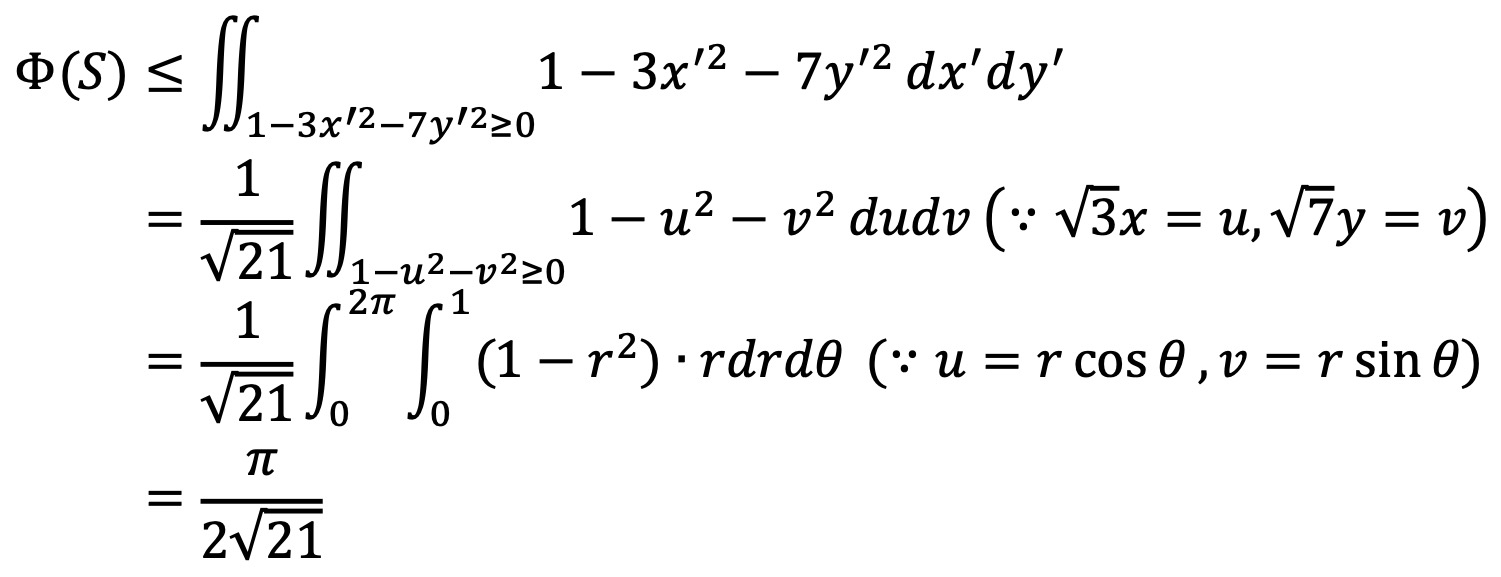
4. 정수 1, 2, ···, n을 재배열하여 얻어지는 임의의 두 순열 (α1, ···, αn)과 (β1, ···, βn)에 대하여 n × n 행렬 A = (aij)는 aij = (1 + αiβj)n-1로 정의된다. 행렬식 det(A)가 취할 수 있는 값을 모두 구하여라. (단, n ≥ 2)
Solution.
주어진 행렬에서 임의의 두 열 혹은 두 행을 서로 뒤바꾸면 행렬식의 부호가 바뀌고 크기는 동일하다.
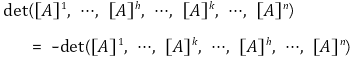
적절히 주어진 행렬의 열과 행의 순서를 바꾸면, αi = i, βj = j가 되도록 할 수 있다.
따라서, A0 = ( (1 + i × j)n-1 )인 행렬이 있을 때, det(A)가 취할 수 있는 값은 ± det(A0)이다.
한편, Vandermonde 행렬식 개념을 검토하자.
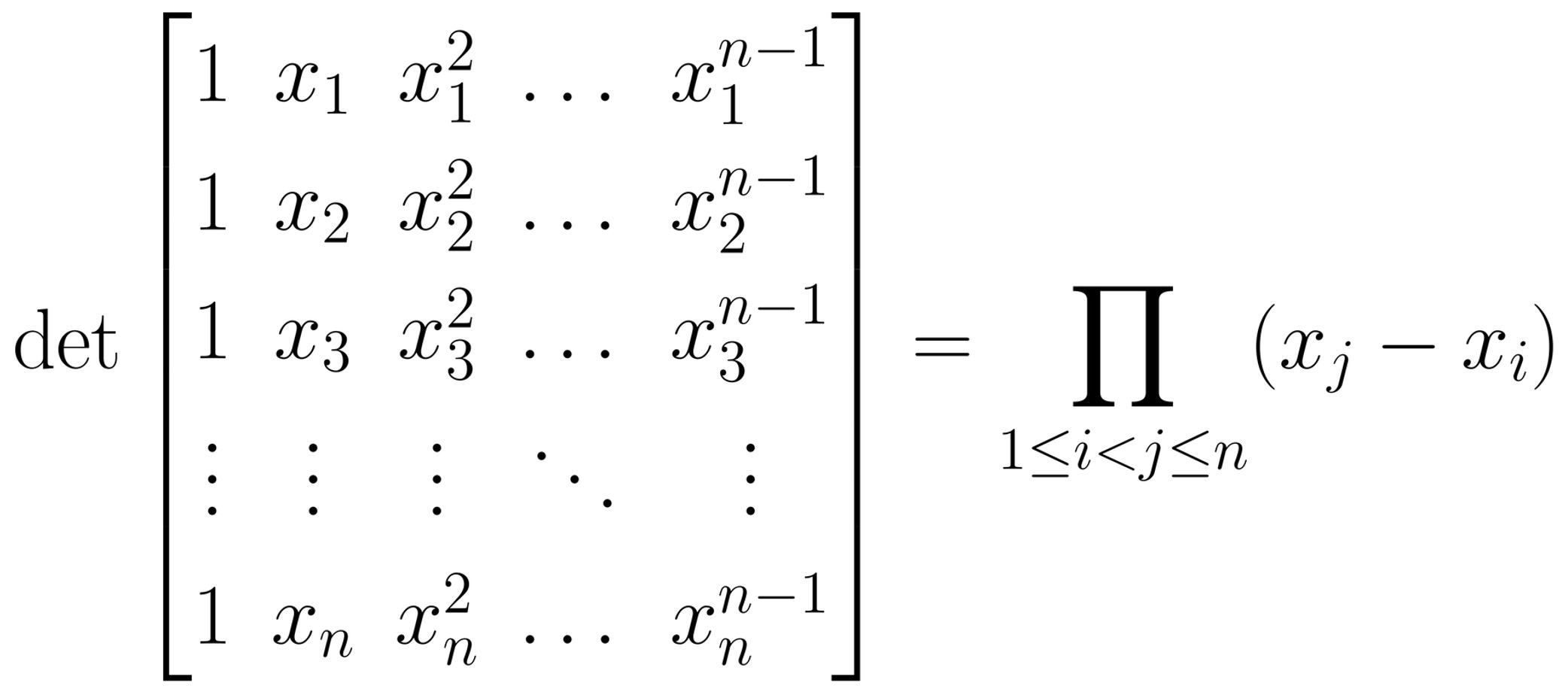
증명
주어진 행렬식은 다항식으로 표현된다.
예를 들어, xn을 보면 그 다항식은 xn에 대하여 n-1차 이하 다항식으로 표현된다.
특정 행벡터에서 다른 행벡터를 빼도 행렬식이 바뀌지 않는다는 사실을 주목하자.
n번째 행과 1번째 행의 차에서 행렬식이 (xn - x1)을 인수로 가짐을 알고, 비슷하게 (xn - x2), ···, (xn - xn-1)을 인수로 가진다.
그러므로 그 다항식은 xn에 대하여 (xn - x1) ··· (xn - xn-1)와 같이 표현된다.
이때, xnn-1이 포함된 항의 계수가 1임을 확인하자.
일반화를 잃지 않고 xn-1, xn-2, ···, x1에 대하여도 비슷하게 표현됨을 알 수 있어 위 식을 증명하였다.
따라서 det(A0)은 다음과 같다.
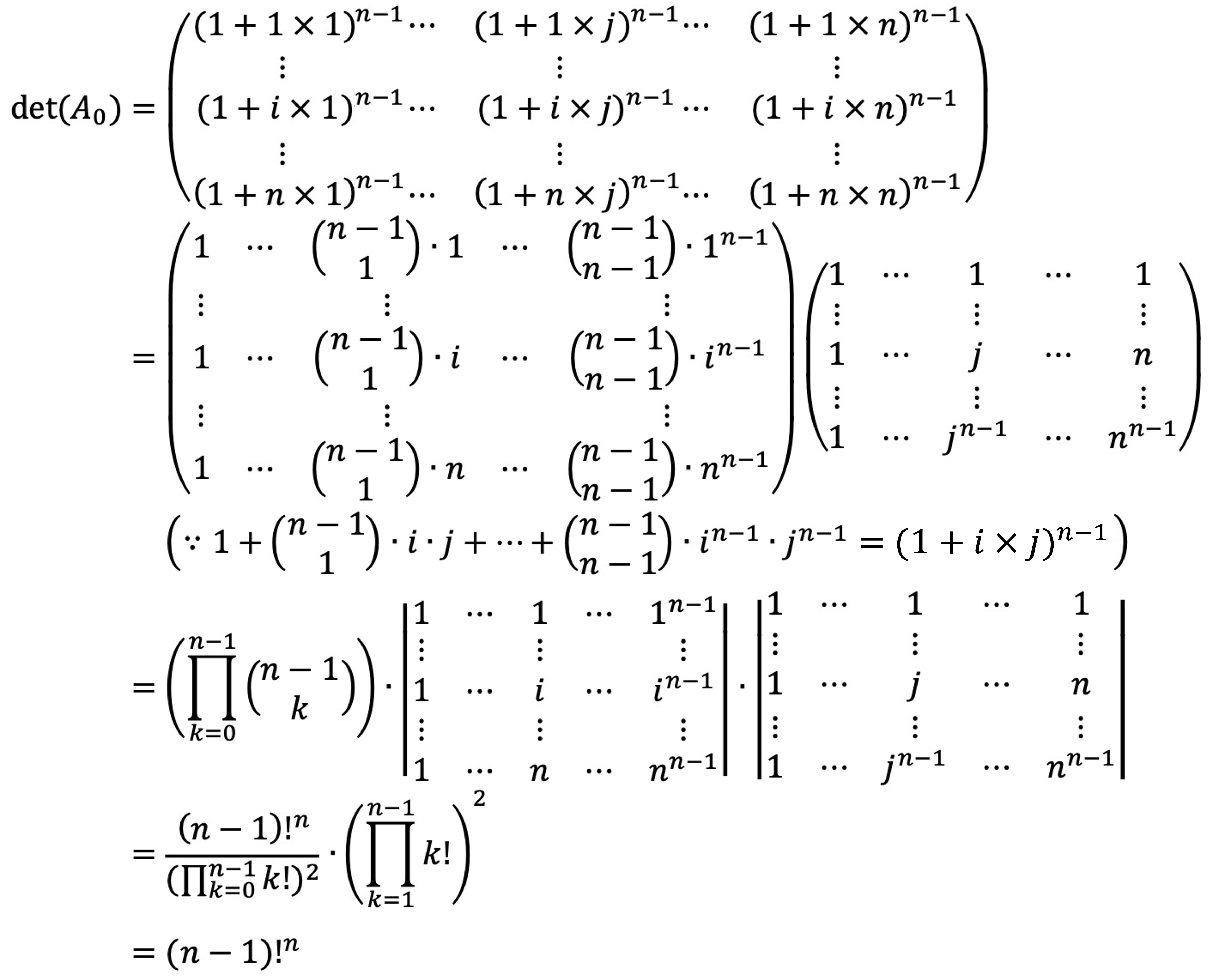
그러므로 det(A)가 취할 수 있는 값은 ± ( (n-1)! )n이다.
5. 크기가 2018 × 2018인 실대칭행렬 A = (aij)의 각 성분 aij가 | aij - 2018 | ≤ 1을 만족한다. 행렬 A의 고유치 중 가장 큰 것을 λ(A)라 할 때, λ(A)가 취할 수 있는 값의 최댓값과 최솟값을 구하여라.
Solution. (저의 풀이)
2 × 2인 실대칭행렬 A = (aij)의 각 성분 aij가 | aij - 2 | ≤ 1을 만족하는 경우를 예로 들자.
이 경우 det(A - λI) = λ2 - (a11 + a22)λ + (a11a22 - a21a12) = 0을 얻을 수 있어 각 (a11, a12, a21, a22)에서 λ(A)는 2개가 나온다.
따라서, 다음과 같이 (a11, a12, a21, a22, λ) 영역에서 2개의 초평면을 나타낼 수 있다.
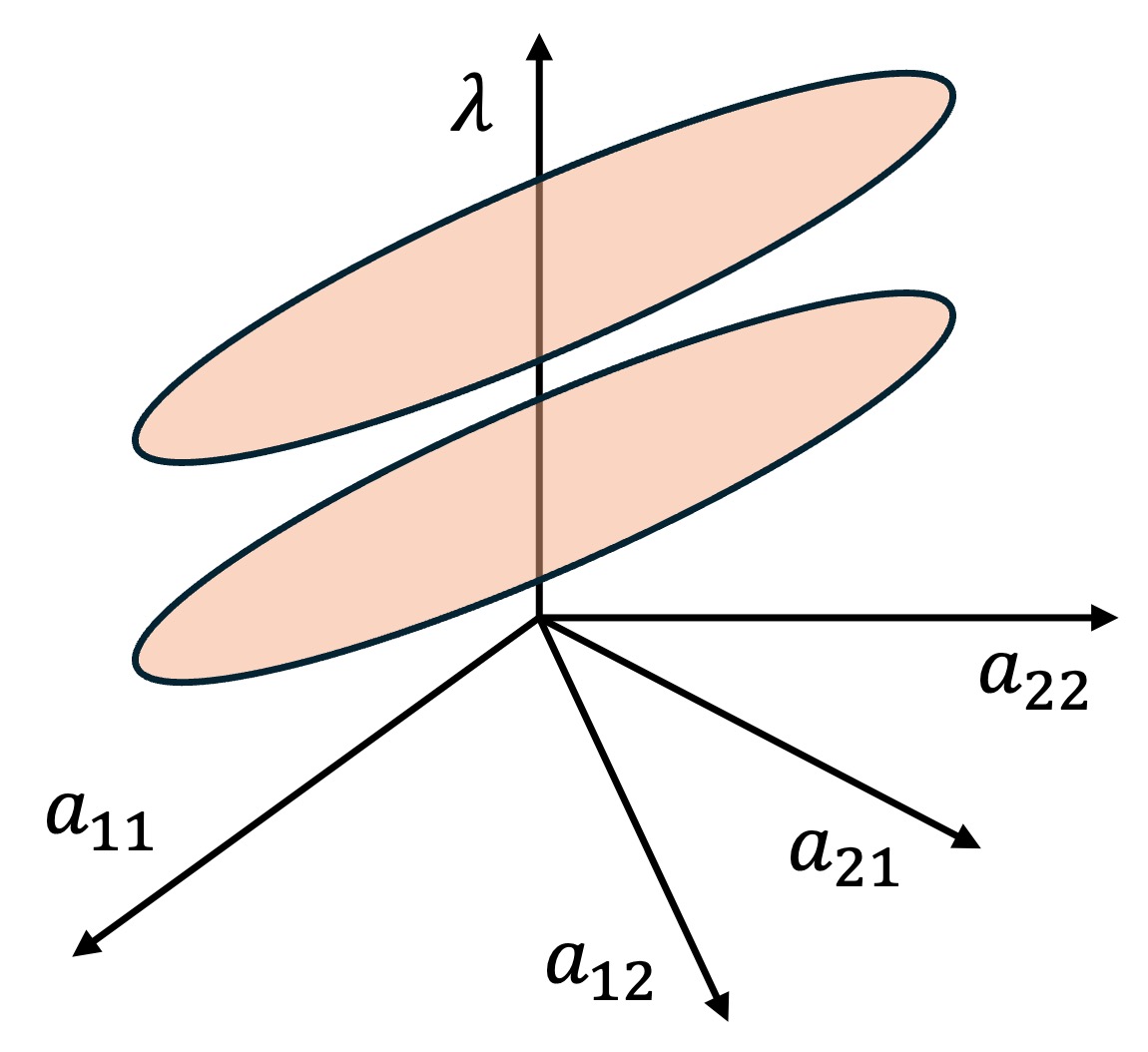
∂λ / ∂aij = 0이라고 두어 λmax가 극값을 갖도록 하는 aij를 탐색할 수 있다.
det(A - λI) = 0의 양변을 aij로 미분하면 다음과 같은 식을 얻을 수 있다.
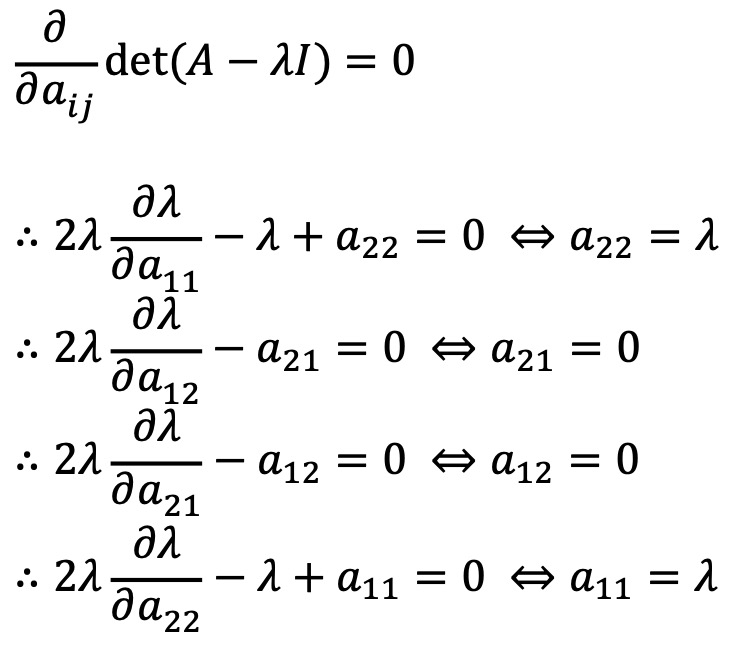
따라서 아주 흥미로운 결과가 나오지만 아쉽게도 일부 aij의 범위가 [1, 3]을 벗어난다.
즉, 주어진 영역이 임의로 잘려진 영역이기 때문에 그 경계조건에서 그 밖에 있는 극점에서 최댓값, 최솟값이 형성되지 않는다.
그런데 ∂2λ / ∂aij2 = 0 (즉, λ가 aij에 대해 선형함수)이므로 λmax가 최댓값 혹은 최솟값이 되려면 aij가 경계값(즉, 1 또는 3)이어야 한다.
이를 일반화하면 주어진 행렬의 aij은 2017 혹은 2019임을 알 수 있다.
한편, 경계조건이 없을 때 3 × 3인 실대칭행렬에서 λmax가 최댓값 혹은 최솟값을 갖는 대각 조건은 다음과 같다.
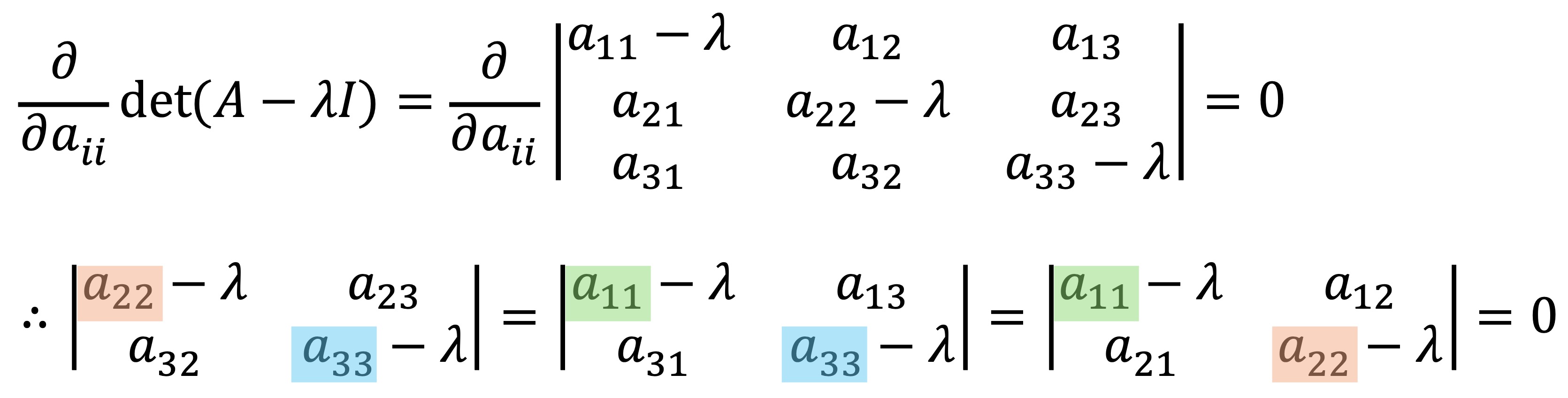
λ의 일차항의 계수가 같다는 사실로부터 a11 = a22 = a33임을 알 수 있다.
따라서, 주어진 행렬의 경우 경계조건이 없을 때, λmax가 최댓값 혹은 최솟값을 가질 시 a11 = a22 = ···가 성립함을 쉽게 알 수 있다.
비슷하게, 경계조건이 없을 때, λmax가 최댓값 혹은 최솟값을 가질 시 aij = aji = ai+1,j+1 = ···을 쉽게 보일 수 있다.
따라서, 앞에서 다룬 시스템 방정식 f(a11, ···, ann, λ) = 0 (n = 2, 3) 은 대각선 단위로 높은 수준의 대칭성을 도출한다.
대칭적인 경계조건을 적용하여 λmax의 최대, 최소를 살피는 과정에서 이러한 대칭성은 깨지지 않는다.
n을 4, 5, ···, 2018로 증가시킨다고 하여 비대칭 연산이 추가되는 것은 아니므로 이러한 대칭성은 유지된다.
따라서 λ가 최댓값 혹은 최솟값을 가질 시 A는 각 대각선 방향으로 모두 같은 값을 가지는 대칭행렬이어야 한다.
2 × 2 행렬에서 각 원소가 1 또는 3일 때, λ의 최대, 최소 조건은 유일하게 결정되며 다음과 같다.
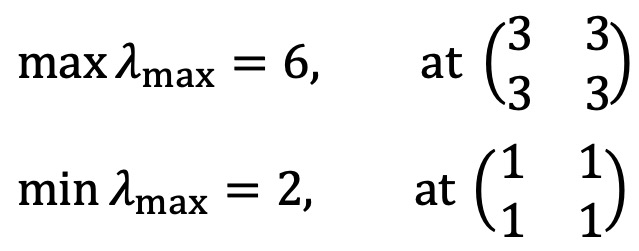
3 × 3 행렬에서 각 원소가 2 또는 4일 때, λ의 최대, 최소 조건은 유일하게 결정되며 다음과 같다.
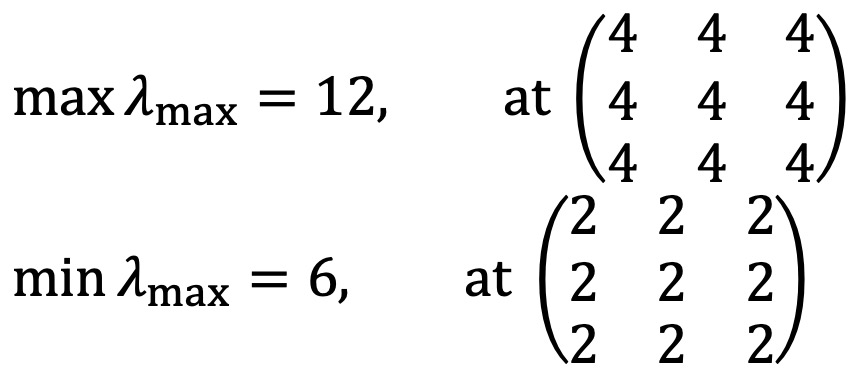
n을 2018로 증가시킨다고 하여 비대칭 연산이 추가되는 것은 아니므로 2018 × 2018 행렬에서 λmax의 최댓값과 최솟값은 비슷하게 결정된다.
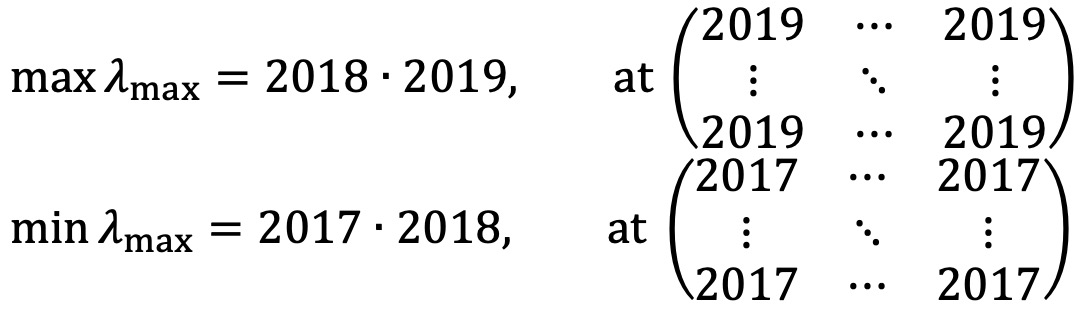
참고로, 모든 원소의 값이 1인 2018 × 2018 행렬은 rank가 1이기 때문에, 고유치 분포가 2018 (크기 n)와 나머지 0들로 결정된다.
Solution. (공식 풀이)
다음을 이용하자.
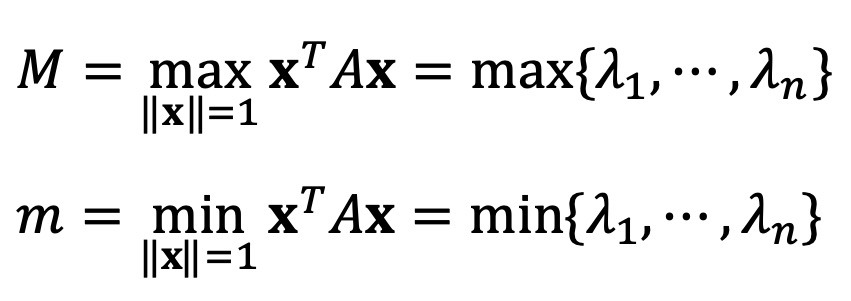
벡터 x = (1, 1, ···, 1)T / √2018 ∈ ℝ2018이라 하면, || x || = 1이며 다음이 성립한다.
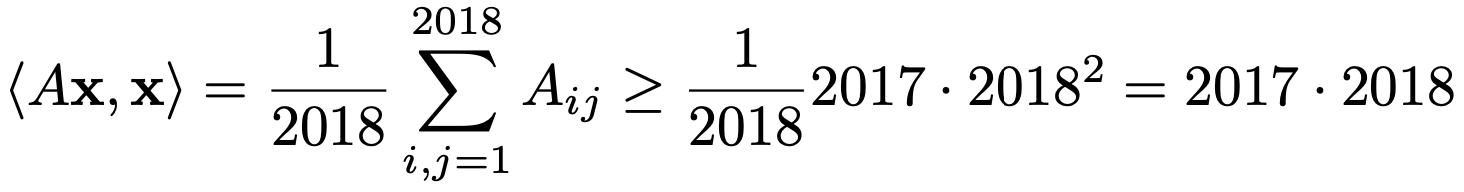
따라서, λ(A) ≥ ⟨Ax, x⟩ ≥ 2018·2017임을 알 수 있다.
가장 큰 고유치에 대응되는 고유벡터를 v = (v1, v2, ···, v2018)T라 하고, |v1|, |v2|, ···, |v2018| 중 최대인 것을 |vi|라 하면 다음과 같다.
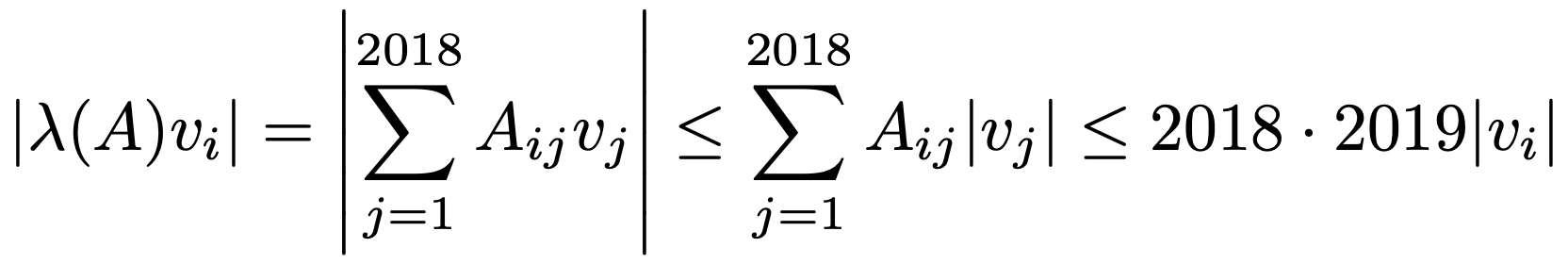
따라서, λ(A) ≤ 2018·2019임을 알 수 있다.
이제, λ(A)가 가질 수 있는 값의 범위가 [2018·2017, 2018·2019]임을 보이기 위하여, 구간 [2017, 2019]에 포함되어 있는 임의의 실수를 a에 대하여, 가장 큰 고유치가 2018·a인 행렬을 만들고자 한다.
먼저, Aij = a로 정의되는 행렬을 생각하면, rank(A) = 1임을 쉽게 알 수 있다.
또한, 벡터 (1, 1, ···, 1)T ∈ ℝ2018은 A의 고유벡터이며 대응되는 고유치가 2018·a임을 쉽게 확인할 수 있다.
따라서, A의 가장 큰 고유치는 2018·a이고 λ(A)가 가질 수 있는 값의 범위는 [2018·2017, 2018·2019]임이 증명된다.
6. 연속함수 f : [0, 1] → ℝ은 열린 구간 (0, 1)에서 미분가능하고, f(0) = 1, f(1) = 0이다. 이때,
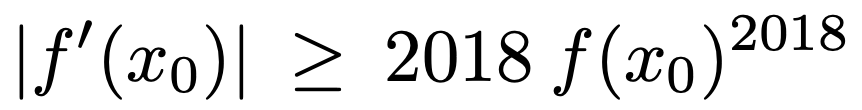
을 만족하는 1보다 작은 양의 실수 x0가 존재함을 보여라.
Solution.
귀류법을 쓰자. 즉, 모든 실수 x ∈ (0, 1)에 대해 | f'(x) | < 2018 f(x)2018이 성립한다고 가정하자.
그러면 다음과 같은 모순이 도출된다.
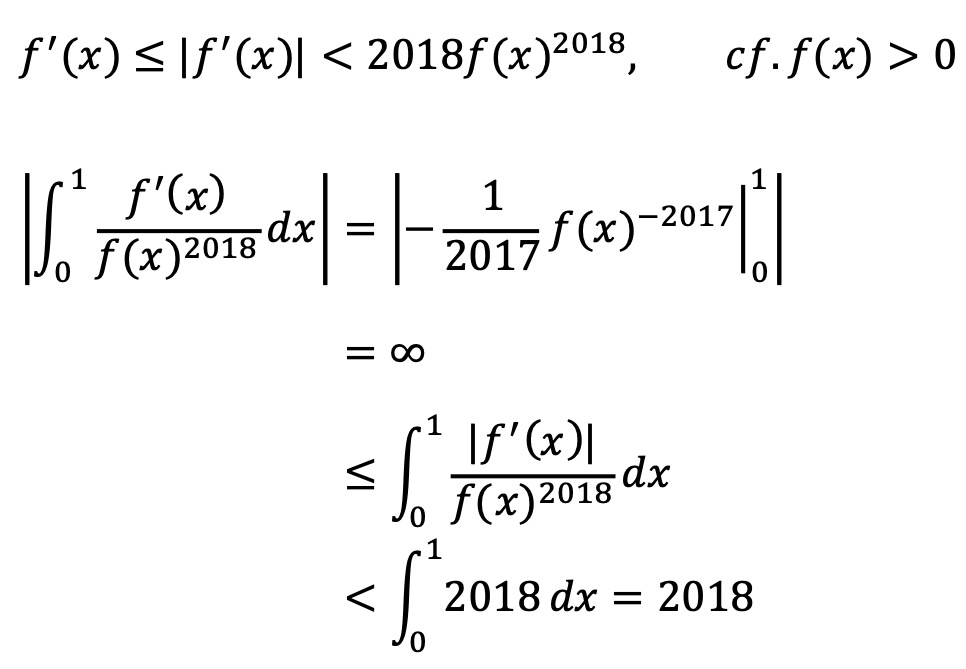
따라서 준 명제를 증명하였다.
7. 크기가 3 × 3인 실행렬 A는 임의의 벡터 v ∈ ℝ3 - {0}에 대하여 vTAv > 0을 만족한다. (단, 행렬 A는 대칭행렬이 아닐 수도 있다.)
⑴ det(A) > 0임을 보여라.
⑵ 대각행렬 D = diag(-1, 1, 1)에 대하여 행렬 AD의 음수인 고유치는 정확히 한 개임을 보여라.
Solution.
⑴
실행렬 A의 행렬식 det(A)는 고유치의 곱과 같다.
예를 들어, A가 3개의 일차독립인 고유벡터를 가진다면, det(A)를 다음과 같이 보일 수 있다.
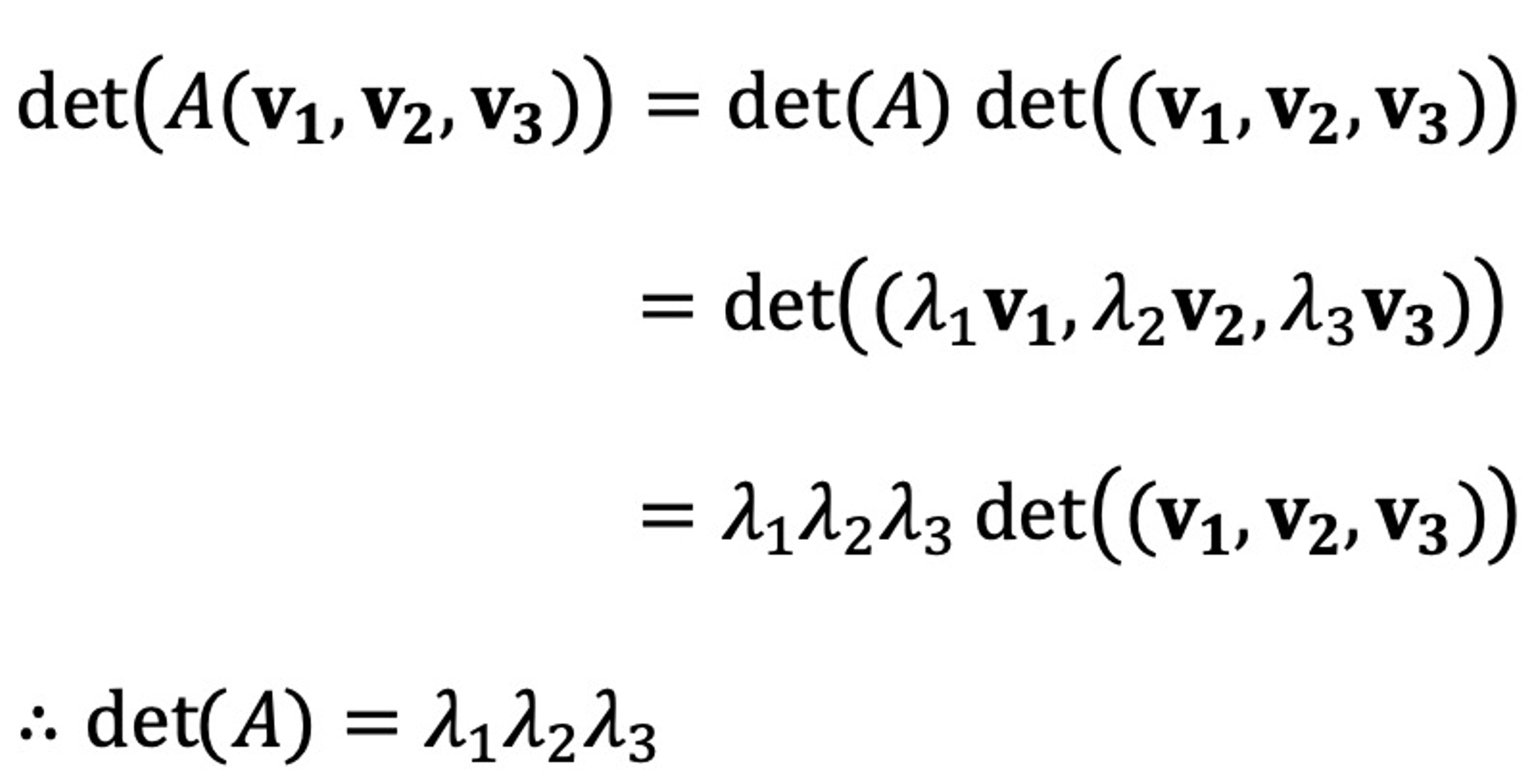
또한, 고유치가 λ1, λ2이고 각각 다중도(multiplicity)가 1, 2이라면, det(A)를 다음과 같이 보일 수 있다.
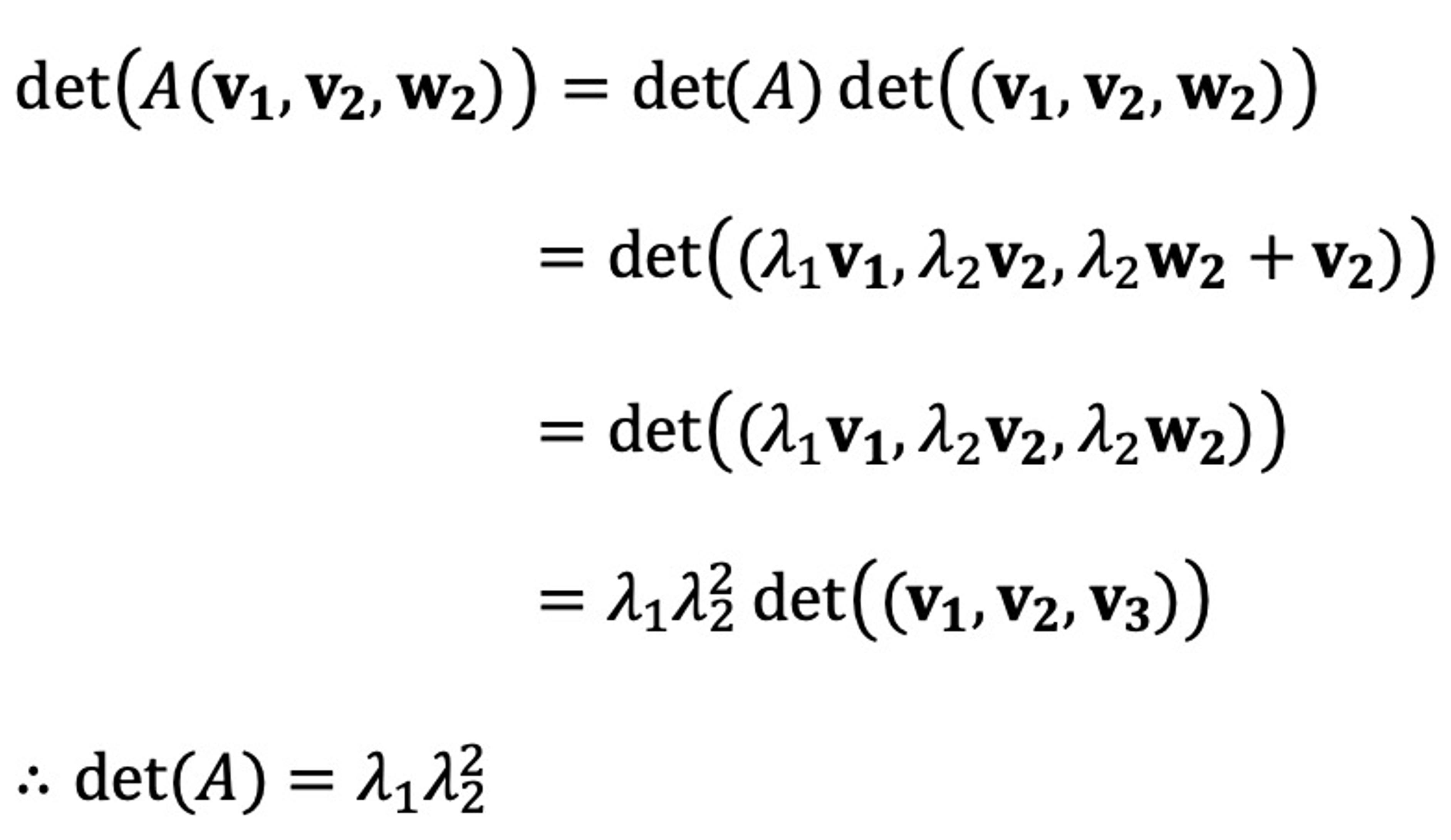
단, w2는 λ2 및 v2에 대응되는 일반화된 고유벡터이다.
이런 식으로 각 경우에 대하여 따지면 고유치의 곱이 det(A)과 같음을 쉽게 보일 수 있음
vTAv > 0이라는 사실로부터 A의 모든 고유치는 0보다 작거나 같은 실수는 아니다.
0 < vTAv = vT(λv) = λ|v|2 ⇔ λ > 0
A의 모든 고유치가 양의 실수라면 det(A) = λ1λ2λ3 (단, λi = λj일 수도 있음) > 0이 성립한다.
A의 고유치가 양의 실수가 아니라 복소수일 수도 있음을 유의하자.
그런데 A의 특성다항식 P(x)가 실계수 다항식이므로, 복소수 z가 P(x) = 0의 근이라면 z의 켤레복소수 z̄도 그 근이다.
따라서 이 경우에도 det(A) = z · z̄ · λ > 0이 성립한다.
그러므로 준 명제를 증명하였다.
⑵
det(AD) = det(A) · det(D) = -det(A) < 0이므로 AD의 고유치들은 다음 중 하나이다.
경우 1. 한 고유치는 음의 실수이고 나머지 두 고유치는 양의 실수
경우 2. 한 고유치는 음의 실수이고 나머지 두 고유치는 복소수
경우 3. 세 고유치가 모두 음의 실수
이제 경우 3이 아님을 보이면 된다.
그런데 경우 3의 경우 vT(AD)v < 0, ∀v ≠ 0이 성립해야 하는데 다음과 같이 반례가 존재하므로 준 명제가 성립함을 보였다.
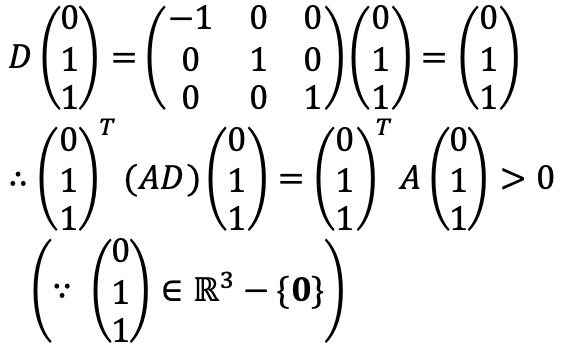
8. 실수열 {an}n≥0은 a0 = 0, 100 / 101 < a100 < 1을 만족하고, 임의의 n ≥ 1에 대하여 다음이 성립한다.
2an - an-1 - an+1 ≤ 2(1 - an)3
⑴ 수열 bn = an - n/(n+1)은 n ≥ 100이면 bn ≤ bn+1을 만족함을 보여라.
⑵ 급수 ∑n=1 to ∞ an / n2의 수렴, 발산을 판정하여라.
Solution.
⑴
n = 100에서 다음이 성립함을 확인하자.
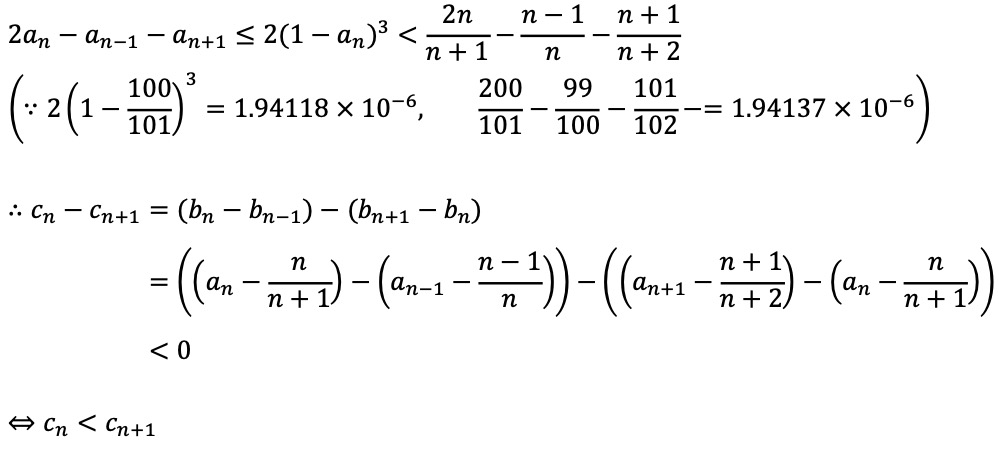
직관을 활용해보자. 부등식이 1개뿐인데, an을 한 번 크게 잡으면 (e.g., 1을 초과) an+1, an+2, ⋅⋅⋅으로 갈수록 빠르게 값이 커진다.
부등식이기 때문에 값이 빠르게 커진다는 사실 이외에 n = 1 ~ 98에서 an이 어떻게 정의되는지에 대한 일반적 정보는 없다.
이 경우 bn ≤ bn+1임을 만족시키는 것은 어렵지 않다.
따라서 an을 최대한 작게 증가시켜서 bn ≤ bn+1이 성립하기 어렵게 만들자.
n = 100에서 an+1 = (an - n / (n + 1)) + (n + 1) / (n + 2)로 최대한 작게 설정할 수 있다.
이때, 위 식은 등호 없는 부등식이므로 an+1를 가능한 것보다 더 작게 설정한 것이라 볼 수 있다.
즉, n = 100에서 an+1 > an - n / (n + 1)) + (n + 1) / (n + 2) ⇔ b100 < b101이 성립한다.
이렇게 an을 가능한 것보다도 더 작게 증가시키면, 0 < b101 - b100 = c100 < cn+1, n ≥ 100이 성립함도 알 수 있다.
즉, n ≥ 100에서 bn ≤ bn+1을 증명하였다.
주석:
위 풀이는 직관을 제공하는 것일 뿐 수학적으로 엄밀하게 풀이를 다시 정리할 필요는 있다.
예를 들어, 2(1 - an)3 < 2n / (n + 1) - (n - 1) / n - (n + 1) / (n + 2)은 따로 증명하지 않았지만 시뮬레이션으로 쉽게 보일 수 있다.

생각컨대, f(x) = (1 - x)3가 x = 1 근처에서 빠르게 감소하는 특성을 수학적으로 잘 표현할 수만 있으면 되지 않을까.
참고로, 필자 같이 직관에 확신이 있다면 위 시뮬레이션 결과를 시험장에서 보여줄 수는 없어도 쉽게 보일 수 있음을 어필할 수 있다.
⑵
우선, an이 빠르게 값이 커질 수 있기 때문에 발산하는 게 일반적이다.
이제 질문은 an을 최대한 작게 증가시켰을 때에는 수렴할 수 있는지이다.
공식 풀이가 발산한다고 명시했는데, 이는 잘못되었고 수렴하는 경우가 존재한다고 생각한다.
a99 = a100 = 100.5 / 101이고 an+1 = max(2an - an-1 - (1 - an)3, 100.5 / 101)가 성립한다고 하자.
이 경우, 2an - an-1 - (1 - an)3 < 100.5 / 101이므로 an+1 = 100.5 / 101이다.
따라서 n ≥ 99에서 an = 100.5 / 101이므로, (준식)은 수렴할 수 있다.
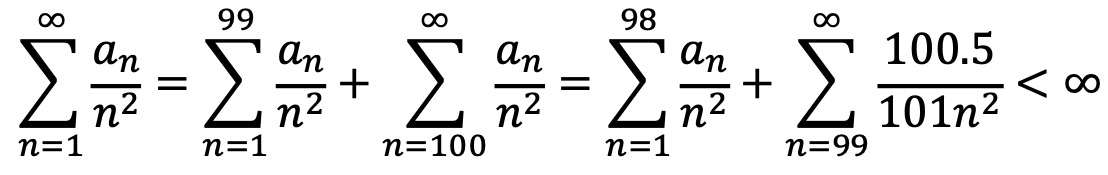
입력: 2025.01.01 17:16