【선형대수학】 2강. 행렬의 계수
2강. 행렬의 계수
추천글 : 【선형대수학】 선형대수학 목차
1. 기저 [본문]
2. 직교집합 [본문]
3. 상공간과 영공간 [본문]
1. 기저(basis) [목차]
⑴ 정의 : 생성집합 중에서 선형독립인 것
⑵ 정리 1. 벡터 공간의 기저의 원소의 개수는 유일함 : 그 개수를 차원(dimension)이라고 함
① 정리 1-1. V가 n차원 벡터공간이고 V의 부분집합을 S ={y1, ···, ym}이라 할 때, n < m이면 S는 선형종속
○ 증명
x1, x2, ···, xn을 V의 기저라고 정의

그런데 m개의 미지수에 n개의 연립방정식이므로 전체 연립방정식이 부정방정식이 되어 선형종속이 됨
② 정리 1-2. 정리 1과 유사하게 n > m이면 S는 생성집합이 아님 : 즉, 벡터의 개수가 부족함
⑶ 정리 2. 벡터 공간의 기저의 존재성 : dim V = n이고 A ={X1, ···, Xn}이 선형독립이면 A는 V의 기저
○ 증명
x가 V의 임의의 기저라 할 때

{X1, ···, Xn}은 생성집합인 동시에 선형독립이므로 V의 기저임
⑷ 정리 3. W가 벡터공간 V의 부분공간이고 dim W = dim V이면 W = V가 성립
○ 증명
W의 기저를 {w1, ···, wn}, V의 기저를 {v1, ···, vn}이라 하자.
v ∈ V이고 v ∉ W인 v가 존재한다고 가정하자. (#)

xn+1 ≠ 0이라면 (#)에 모순됨

따라서 xn+1 = 0이어야 (#)을 만족하고 그 결과 w1, ···, wn, v는 선형독립

이는 V가 n차원 벡터이고 V의 부분집합을 S = {y1, ···, ym}이라 할 때, n < m이면 S는 선형종속이라는 명제와 모순따라서 그러한 v는 존재하지 않으므로 W = V가 성립함
⑸ 정리 4. 초평면{(x1, x2, ···, xn)' | p1x1 + p2x2 + ··· + pnxn = 0, p1 ≠ 0}의 기저로 다음 n-1개를 선택할 수 있음

⑹ 정리 5. 기저에 대한 선형사상의 변환행렬
① V, W : 유한 차원 벡터공간
② T : V → W : 선형변환
③ B ={v1, v2, ···, vn}: V의 기저
④ B' ={w1, w2, ···, wm}: W의 기저
⑤ 수식화

⑥ 기저 B, B'에 관한 T의 행렬

⑺ 응용 1. 기저의 확장 : 행간소 사다리꼴(RREF) 이용

Figure. 1. v1, v2, v3가 주어져 있을 때 ℝ5를 span하도록 기저를 확장하는 과정
2. 직교집합 [목차]
⑴ 직교(orthogonal)

⑵ 직교집합(orthogonal set) : 집합 내 서로 다른 임의의 원소가 직교한 경우. 직교집합은 선형독립성을 만족함

⑶ 직교기저(orthogonal basis) : 직교집합 S가 V의 기저인 경우
⑷ 정규직교기저(orthonormal basis) : S가 직교기저이고 모든 j에 대하여 || xj || = 1인 경우
① 정규직교기저로 구성된 행렬 U에 대하여, UTU = I ⇔ U-1 = UT를 만족함
⑸ 표준기저(standard basis) : ℝn의 기저 중 하나인 U = ℰn ≡ {e1, e2, ···, en}을 지칭함
⑹ 좌표계(coordinates system)

⑺ 직교좌표계(orthogonal coordinates system) : 표준기저에 의하여 결정되는 좌표계
⑻ 투영(projection)
① 임의의 벡터를 정규직교기저로 구성된 이미지 (예 : 직선, 평면) 위에 투영하는 변환

○ 파이썬 코드 예시
y1 = np.array([1, 2, 3, 4])
y2 = np.array([8/3, 4/3, 0, -4/3])
u1 = y1 / np.linalg.norm(y1)
u2 = y2 / np.linalg.norm(y2)
U = np.column_stack((u1, u2))
UUT = np.dot(U, U.T)
v = np.array([1, 1, 2, 2])
proj_v = np.dot(UUT, v)
proj_v
② 저차원 주성분 공간으로 데이터 투영 및 복원 (cf. PCA)
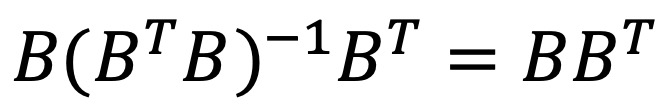
○ 행렬 B : 주로 정규 직교 행렬 B
○ 투영 공간 : B가 정의하는 저차원 공간으로 투영한 뒤 복원
③ 최소 제곱 문제를 풀기 위해 데이터 투영 : 임의의 행렬 A가 주어져 있을 때 Ax = b 위에 투영하는 변환

○ 행렬 A : 임의의 A
○ 투영 공간 : A의 컬럼 스페이스
④ 주어진 데이터를 Ax = b에 선형 근사 (ref)

⑼ 그람-슈미트 직교화 과정(Gram-Schmidt orthogonalization process)
① 정의 : 임의의 기저로부터 직교기저를 얻는 방법

② (주석) 직관적 해석 : yk를 구할 때 주어진 xk에 y1, ···, yk-1로 수정을 하는 느낌
③ 정규직교기저를 얻으려면 y1, ···, yk 등의 직교기저를 얻고 난 뒤 이들을 정규화해야 함
3. 상공간과 영공간 [목차]
⑴ 개요
① 상공간(image space) : 컬럼 공간(column space)이라고도 함

② 계수(rank) : rank (T) 또는 rk (T)로 나타냄

③ 핵(kernel) 또는 영공간(null space)

④ 퇴화차수(nullity) : nullity (T) 또는 nul (T)로 나타냄

⑤ 예 1. T(x, y, z) = (3x - 2z, y + z)'

⑥ 예 2. T(x, y) = (x - 4y, x + 2y, 2x - y)'

⑦ 예 3. 선형사상 T가 행렬로 표현된 경우 : 열벡터들 중 선형독립인 것들의 최대 개수는 2이므로,

⑧ 예 4. 선형사상 T가 행렬로 표현된 경우

⑵ 정리 1. 계수정리 : 임의의 행렬의 열벡터들의 계수와 행벡터들의 계수는 같음
⑶ 정리 2. 행렬 A ∈ ℝn×m의 rank는 A = B·Ct, B ∈ ℝn×r, C ∈ ℝm×r인 최소의 r이기도 함
① 2-1. 임의의 n × n 대칭 양반정부호 행렬(symmetric positive semi-definite matrix)의 계수가 r인 필요충분조건

⑷ 정리 3. rank(AB) ≠ rank(BA)

⑸ 정리 4. 양의 정수 n에 대하여 n × n 실행렬 A가 An+1 = O을 만족하면 An = O이 성립 (단, O는 영행렬) (ref)
○ 증명
귀류법을 쓰자.
n × n 실행렬 A가 An+1 = O을 만족하면서 An ≠ O라고 가정하자.
그러면 0 ≠ v1 ∈ Im(An)인 v1을 찾을 수 있다. (단, 0은 영행렬이다.)
이때 Av1 ∈ Im(An+1) = Im(O) = 0이므로 Av1 = 0이다.
따라서, Anv1 = 0으로부터 v1 ∈ Ker(An)임을 쉽게 알 수 있다.
그러므로 Anv1 ≠ 0이면서 (∵ v1 ∈ Im(An), An ≠ O), Anv1 ∈ 0이므로 (∵ v1 ∈ Ker(An)) 모순이다.
가정이 틀렸으므로, n × n 실행렬 A가 An+1 = O를 만족하면 An = O가 성립한다.
⑹ 정리 5. rank-nullity theorem : 사상 T : U → V가 선형사상이고 dim U = n이면 다음 관계가 성립함

○ 증명

① 정리 5-1. 선형 사상 T가 전사함수이면 T는 단사함수이고, 그 역도 성립함

② 정리 5-2. m × n 행렬 A와 n × p 행렬 B에 대해 다음 등식이 성립
rank(AB) = rank(B) - dim[Ker(A) ∩ Im(B)]
○ 증명 1

○ 증명 2. rank-nullity theorem 이용

③ 정리 5-3. m × n 행렬 A에 관하여 다음 등식이 성립함
Im(A) = Im(AA')
○ 증명

Im(A')의 어떤 원소 A'x가 동시에 ker(A)의 원소라고 가정

따라서 dim [ker(A) ∩ Im(A')] = 0이므로 다음이 성립함

④ 응용 1. 버킹엄의 파이 정리(Buckingham PI theorem) 어떤 n개의 독립변수가 m개의 기본차원으로 표시된다고 할 때, 다음 변환을 찾을 수 있음 (단, ∏i는 무차원량)
g(x1, x2, ..., xn) = 0 ⇔ G(∏1, ∏2, ..., ∏n-m) = 0
⑺ 정리 6. 프로베니우스 rank 부등식(Frobenius' rank inequality) : k × ℓ 행렬 A, ℓ × m 행렬 B, m × n 행렬 C에 대해 다음 부등식이 성립
rank(AB) + rank(BC) ≤ rank(B) + rank(ABC)
○ 증명

입력: 2020.04.25 10:03