제 36회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 36회 전국 대학생 수학경시대회
제 2 분야
2017년 (10:00 - 13:00)
1. 차수가 3 이하인 모든 실계수 다항식으로 이루어진 실벡터공간을 V라 하고 선형사상 T : V → V를 다음과 같이 정의한다.
T(P(x)) = x4P(x)를 (x-1)2(x+1)2으로 나눈 나머지
이때, T의 특성다항식을 구하여라.
Solution.
P(x) = ax3 + bx2 + cx + d ≡ (a, b, c, d) ∈ ℝ4로 정의하자.
(a, b, c, d)를 e1, e2, e3, e4 각각으로 두면 선형사상 T를 나타내는 4 × 4 행렬을 구할 수 있다.

따라서 T의 특성다항식은 다음과 같다.

2. 다음 미분방정식의 해 u(t)를 구하여라.
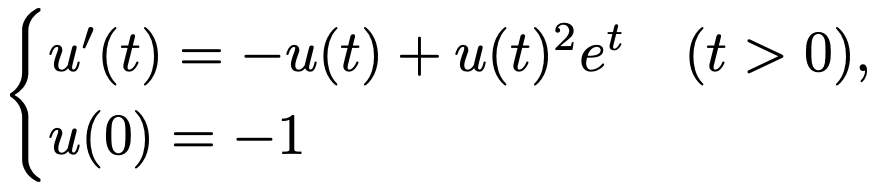
Solution.
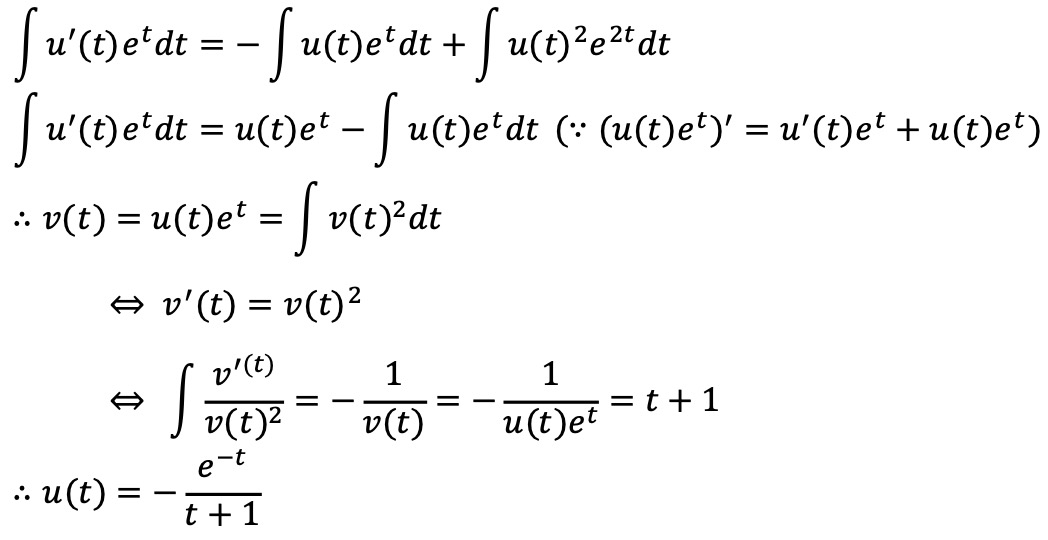
3. 양의 정수 n에 대하여 n × n 실행렬 A가 An+1 = O을 만족하면 An = O임을 보여라. (단, O는 영행렬이다.)
Solution.
귀류법을 쓰자.
n × n 실행렬 A가 An+1 = O을 만족하면서 An ≠ O라고 가정하자.
그러면 0 ≠ v1 ∈ Im(An)인 v1을 찾을 수 있다. (단, 0은 영행렬이다.)
이때 Av1 ∈ Im(An+1) = Im(O) = 0이므로 Av1 = 0이다.
따라서, Anv1 = 0으로부터 v1 ∈ Ker(An)임을 쉽게 알 수 있다.
그러므로 Anv1 ≠ 0이면서 (∵ v1 ∈ Im(An), An ≠ O), Anv1 ∈ 0이므로 (∵ v1 ∈ Ker(An)) 모순이다.
가정이 틀렸으므로, n × n 실행렬 A가 An+1 = O를 만족하면 An = O가 성립한다.
4. 계수가 유리수인 다항식 f(x, y)는 임의의 정수 m, n에 대하여 f(m, n)이 정수이다. 이때, 다항식 f(x, y)는 적당한 정수 cij에 대하여 다음과 같이 표현됨을 보여라.
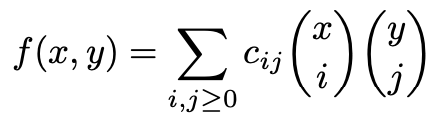
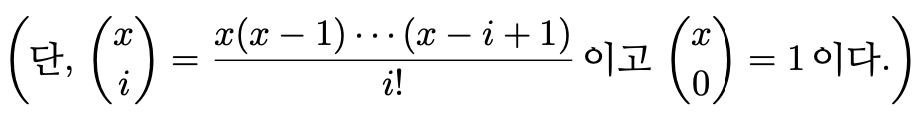
Solution.
다항식 f(x, y)는 f(x, y) = ∑a,b≥0 da,b xa yb (단, da,b는 유리수)로 나타낼 수 있다.
문제 이해 측면에서, f(x, y) = xy(x+y) / 2는 계수가 정수가 아닌 유리수이지만 임의의 정수 m, n에 대하여 f(m, n)이 정수임을 확인하자.
우선 da,b xa yb = ∑0≤i≤a,0≤j≤b cij xCi yCj인 유리수 cij가 있음을 보이자.
이때, i=a, j=b인 경우에 xCi yCj가 최고차항인 xa yb를 가질 수 있어 da,b = cab / (a! b!)임을 알 수 있다.
한편, xCi yCj = (s0x0 + s1x1 + ··· + saxa) · (t0y0 + t1y1 + ··· + tbyb)와 같이 나타낼 수 있음을 확인하자.
나머지 ci,j는 각 항에서 도출되는 x0y0, x1y0, x0y1, x1y1, ···, xa-1yb-1, xayb-1, xa-1yb이 각각 합해서 0이 되도록 적당히 정의된다.
따라서 다음과 같이 (a+1)(b+1)개의 변수에 관한 일원 연립방정식을 푸는 것과 같아 cij는 유일하게 결정된다고 할 수 있다.
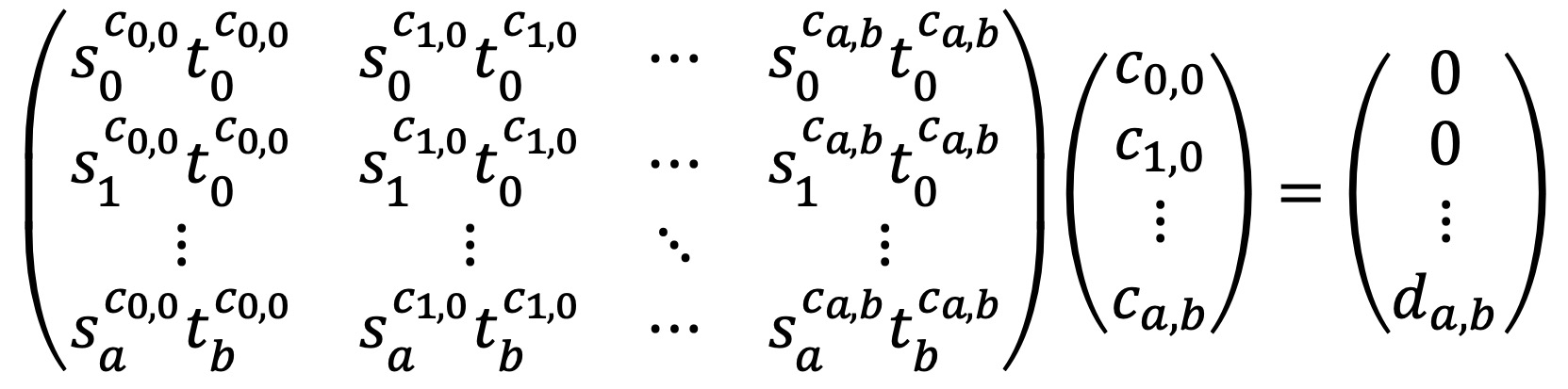
예를 들어, 위 행렬에서 첫 번째 방정식 s0c0,0 t0c0,0 + s0c1,0 t0c1,0 + ··· + s0ca,b t0ca,b = 0은 각 (i, j)에서 x0 y0의 계수를 합한 것이다.
단, c0,0 등은 지수로 들어간 것은 아니고 그저 어떤 항에서 온 것인지를 표시하는 위첨자이다.
그렇다면, 이 경우 반드시 cij는 유리수여야 하는가?
x ∈ ℤ, y ∈ ℤ을 +∞로 발산시키면, 차수가 높을수록, 차수가 같더라도 발산 경로에 따라 특정 변수의 차수가 높을수록 더 빠르게 발산한다.
발산하는 경우에도 여전히 xi yj의 계수는 da,b 또는 0이어야 하므로, 차수가 높을수록 그 계수가 유리수임을 알 수 있다.
왜냐하면 x, y → ∞로 발산하는데 계수가 무리수인 항이 한 번 나타나면 그것보다 낮은 차수의 항에서 그 무리수를 상쇄할 수 있는 방법이 없다.
따라서 모든 i, j에 대하여 cij는 유리수이다.
그러므로 계수가 유리수인 임의의 다항식 f(x, y)는 ∑0≤i≤a,0≤j≤b cij xCi yCj의 선형합이라고 할 수 있다.
따라서, f(x, y) = ∑0≤i,0≤j cij xCi yCj로 나타낼 수 있다 (즉, i, j의 범위 중 상한을 제외한 것에 불과하다).
이제, 유리수인 cij가 정수임을 보이자.
조합론에 의해 양의 정수 x, y에 대하여 xCi yCj가 정수임을 안다.
따라서 f(x, y)는 각 유리수 계수에 정수를 곱하여 선형합을 해준 형태이다.
만약 특정 계수의 분모가 고유한 소인수를 갖는다면 x, y가 그 소인수를 제외한 모든 다른 분모들의 곱을 취하면 f(x, y)는 정수가 아니다.
따라서 모든 정수가 아닌 유리수 계수는 분모가 동일하고 이를 m이라고 하자.
이때 모든 양의 정수 x, y에 대하여 f(x, y)가 언제나 정수가 되도록 할 수 없다.
왜냐하면 mod 연산 하에서 연립 방정식을 푸는 상황인데 방정식이 너무 많이 존재하는 상황이다.
따라서 정수가 아닌 유리수 계수는 존재하지 않는다.
그러므로 존재하는 (cij)가 정수임을 보였다.
참고로, 일반성의 원리에 따르면 특정 분모 m가 f(x, y)를 기술하는 특성으로 나타날 이유는 없다. (수학적으로 증명할 수도 있다.)
5. 행렬
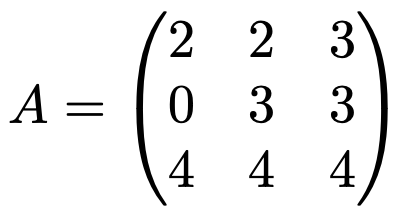
에 대하여 실행렬 B가 AB = BA를 만족하면 적당한 실수 a, b, c에 대하여 B = aA2 + bA + cI가 성립함을 보여라.
Solution.
A의 고유치는 다음과 같다.
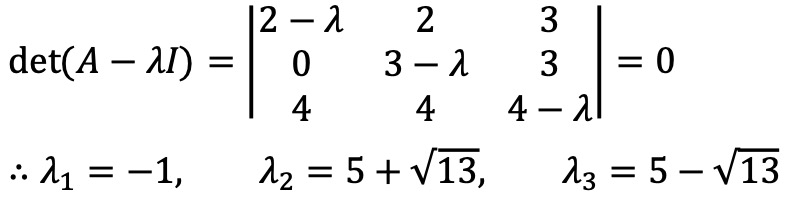
A의 고유치는 모두 다르기 때문에 A는 A = PDP-1(단, D는 대각행렬)와 같이 대각화 가능하다.
AB = BA가 성립하므로 M := P-1BP가 대각행렬 D와 가환(commutant)함을 의미하여, M도 또한 대각행렬임을 의미한다.
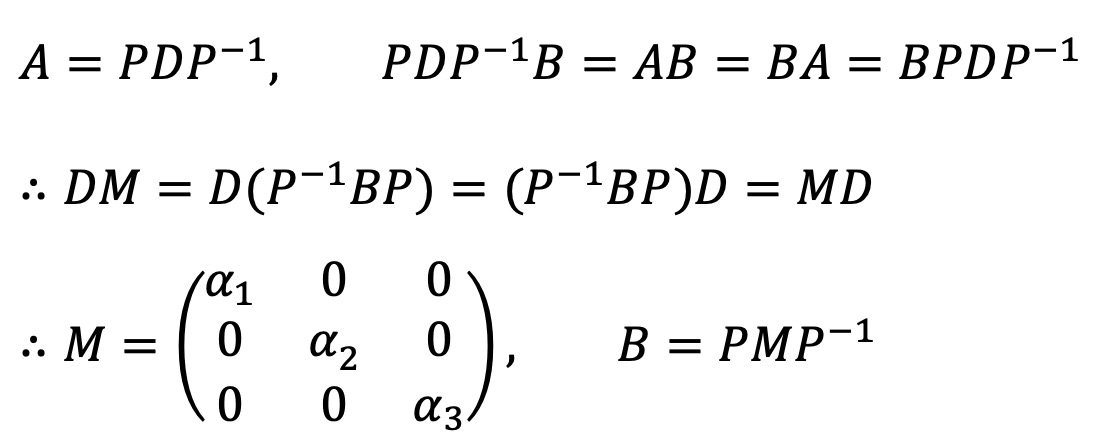
그런데 D를 구성하는 고유치가 모두 달라서 다음 식을 성립하게 하는 3원 일차방정식을 언제나 풀 수 있어서 준 명제가 성립한다.
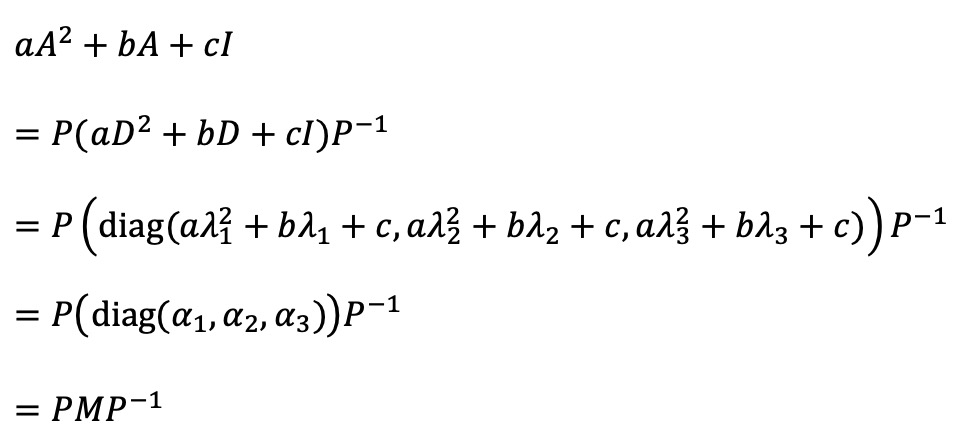
6. 양의 정수 n (n ≥ 3)에 대하여 n × n 실행렬 A = (aij)가 다음 조건을 만족하면 A는 가역행렬임을 보여라.
조건 1. 모든 i, j에 대하여 aij > 0이다.
조건 2. 모든 i에 대하여 2aii = ∑j=1 to n aij이다.
Solution.
공식 풀이를 참고하였다.
행렬 A의 영공간 Ker(A)이 0임을 보이면 된다.
Ax = 0인 벡터 x = (xi) ≠ 0이 존재한다고 하면, 일반성을 잃지 않고 xi는 실수라고 가정할 수 있다.
이제 0 ≠ |xk| = max{ |x1|, |x2|, ···, |xn| }이라 가정하면 다음을 얻을 수 있다.
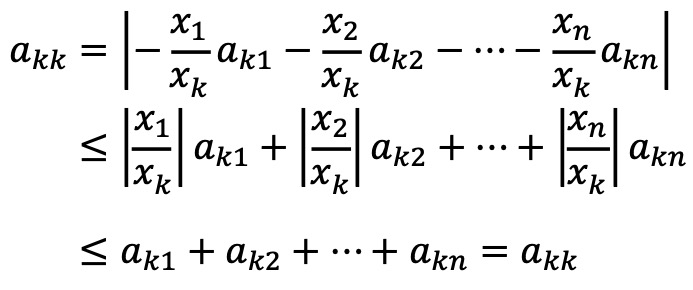
등호가 성립하기 위해서는 -xk = x1 = x2 = ··· = xn이 성립한다.
한편 정수 j ≠ k에 대하여, 2ajk = ∑i=1 to n aji = 2ajj가 성립하므로 ∑i≠j,k aji = 0이 성립한다.
가정에 의하여 이는 모순이다.
그러므로 행렬 A의 영공간 Ker(A)은 0이므로 det(A) ≠ 0으로부터 A는 가역행렬임을 알 수 있다.
7. 수열 {an}은 모든 항이 양수인 감소하는 수열이고, 0 < θ < π/2이다. 다음이 성립함을 보여라.
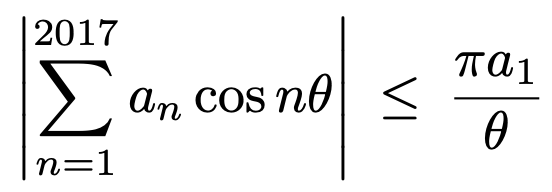
Solution.
위 그림과 같이 0 < x < π / 2에서 sin x ≥ 2x / π임을 이용하면, (준식)을 유도할 수 있다.
참고로, Bn의 일반항을 구하는 방법은 두 가지가 있다.
방법 1. 복소수 지수함수의 등비수열
방법 2. 수학적 귀납법
8. 다음 극한값을 구하여라.
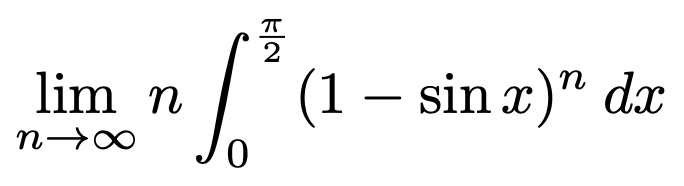
Solution.
수렴값은 다음과 같이 보일 수 있다.
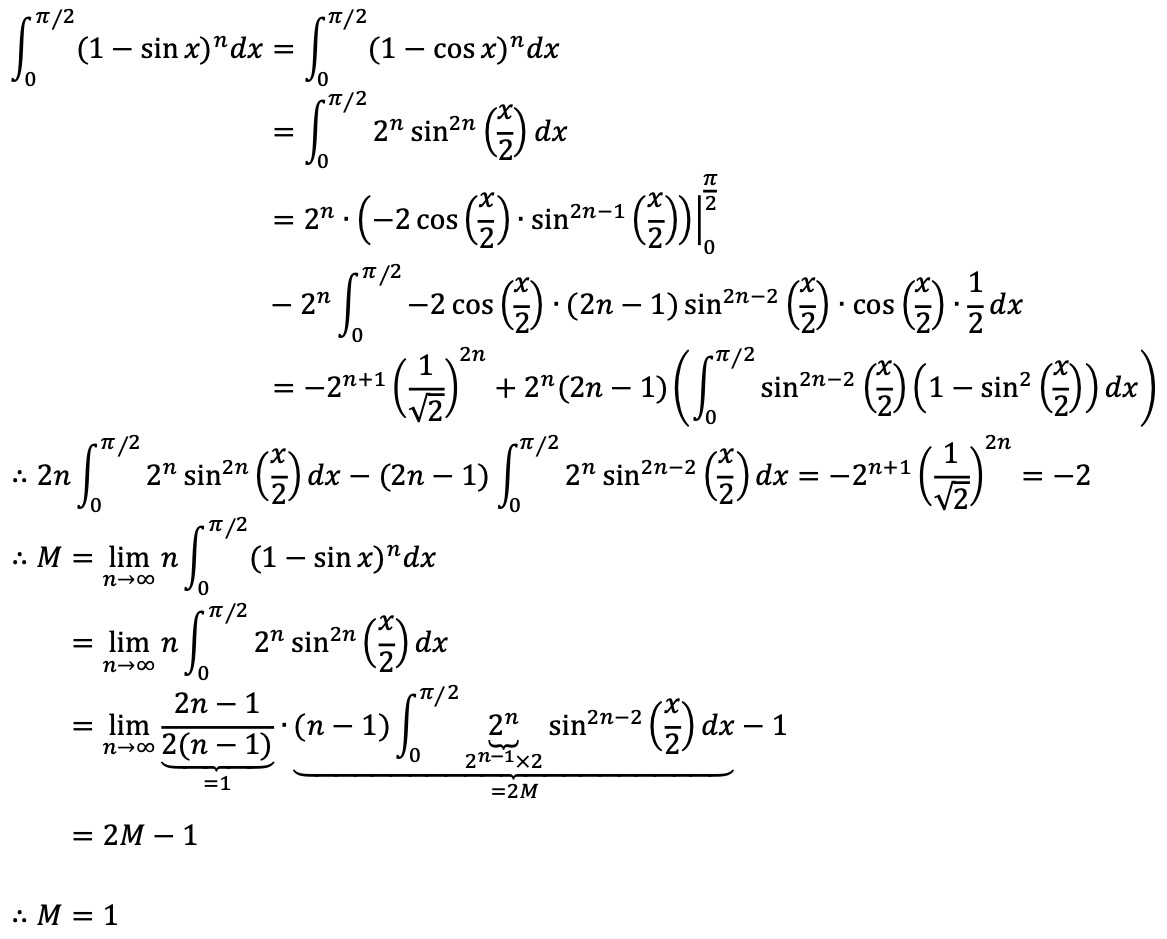
수렴성은 다음과 같이 보일 수 있다.
① M이 위로 유계임을 확인한다.
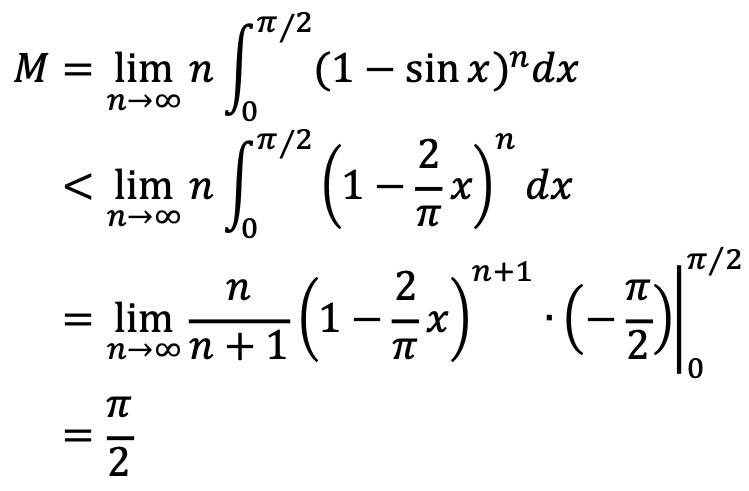
② M이 아래로 유계임을 확인한다. 즉, M ≥ 0이다.
③ 완비성 공리 및 수렴값을 보이는 과정에 의해 M < ∞이 성립하면 M은 수렴한다.
입력: 2025.02.28 09:36
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 35회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.04.20 |
|---|---|
| 【대수경】 제 35회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2025.03.18 |
| 【대수경】 제 36회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2025.03.01 |
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.01.28 |
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 1 분야 (4) | 2025.01.06 |








최근댓글