제 35회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 35회 전국 대학생 수학경시대회
제 2 분야
2016년 (10:00 - 13:00)
1. 다음 극한값을 구하여라 (단, log는 자연로그).

Solution.
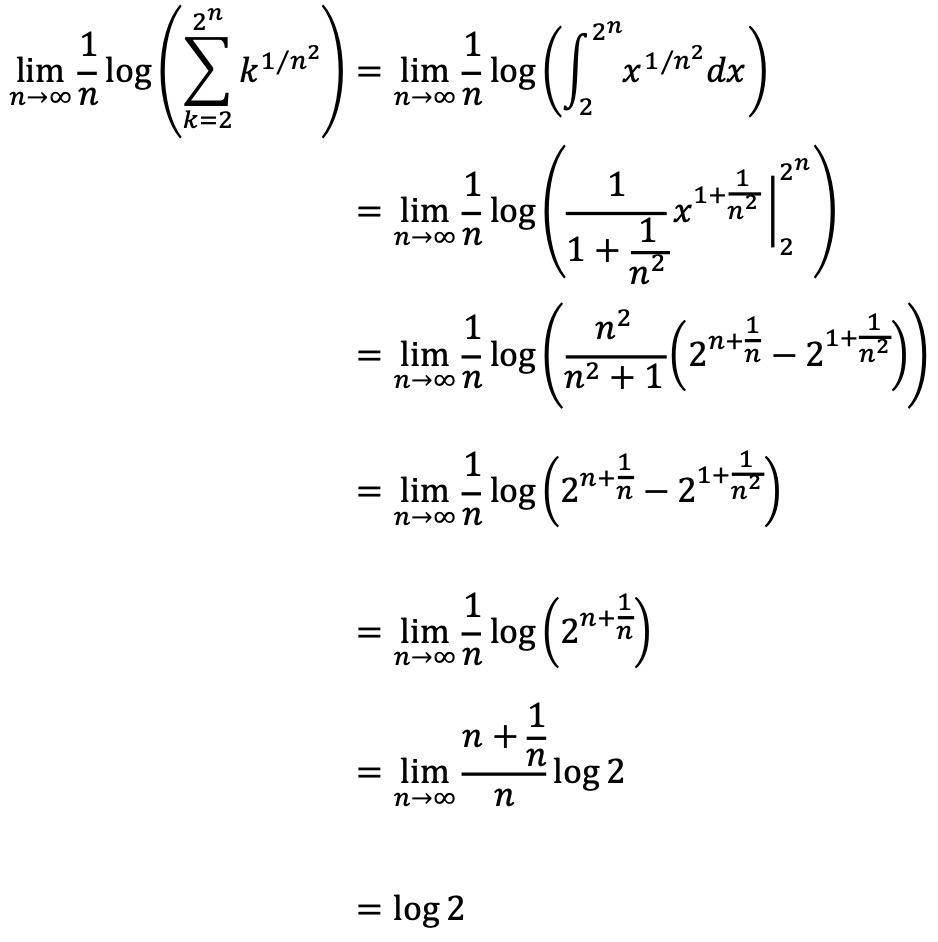
2. 실수 a, b가 a2 + b2 ≤ π2 / 4를 만족할 때, 다음 부등식을 증명하여라.

Solution.

3. 양의 정수 n에 대하여 크기가 n × n인 실행렬 A가 서로 다른 n개의 양의 고유치를 가질 때, B2016 = A를 만족하는 실행렬 B의 개수를 구하여라.
Solution.
A가 서로 다른 n개의 고유치를 가지고 있으므로 A는 대각행렬 DA, 정칙행렬 P에 대하여 다음과 같이 대각화 가능하다.
A = PDAP-1
한편, AB = B2016·B = B2017 = B·B2016 = BA이므로 A와 B는 가환(commutant)이다.
따라서 B도 대각행렬 DB, 위와 동일한 정칙행렬 P에 대하여 다음과 같이 대각화 가능하다.
B = PDBP-1, B2016 = PDB2016P-1
그러므로 A의 각 고유치 λA,i, i = 1, ···, n와 B의 각 고유치 λB,i, i = 1, ···, n에 대하여 다음과 성립한다.
λA,i = λB,i2016
따라서, λB,i = ± 2016√λA,i = ± λA,i1/2016이 성립한다.
그러므로 λB,1, ··, λB,n이 부호 때문에 각각 2가지 경우가 존재하므로, 실행렬 B는 2n개가 존재한다.
4. 다음 미분방정식을 만족하는 함수 y(t)에 대하여 함숫값 y(π/4)를 구하여라.
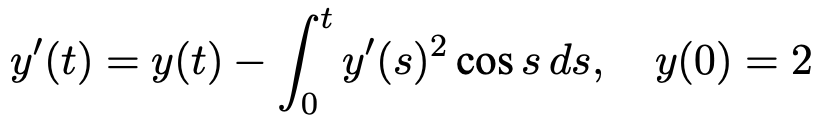
Solution.

5. 연속함수 f : [-π/4, π/4] → [-1, 1]가 구간 (-π/4, π/4)에서 미분가능할 때, 다음 부등식을 만족하는 점 x0가 구간 (-π/4, π/4)에 존재함을 보여라.

Solution.
귀류법을 사용하여 f'(x) > 1 + f(x)2 혹은 f'(x) < -(1 + f(x)2)이라고 가정하자.
f(x)는 연속이므로 f'(x) > 1 + f(x)2와 f'(x) < -(1 + f(x)2) 중 하나만 성립한다.
우선, f'(x) > 1 + f(x)2이라고 가정하면 다음과 같은 모순이 있다.
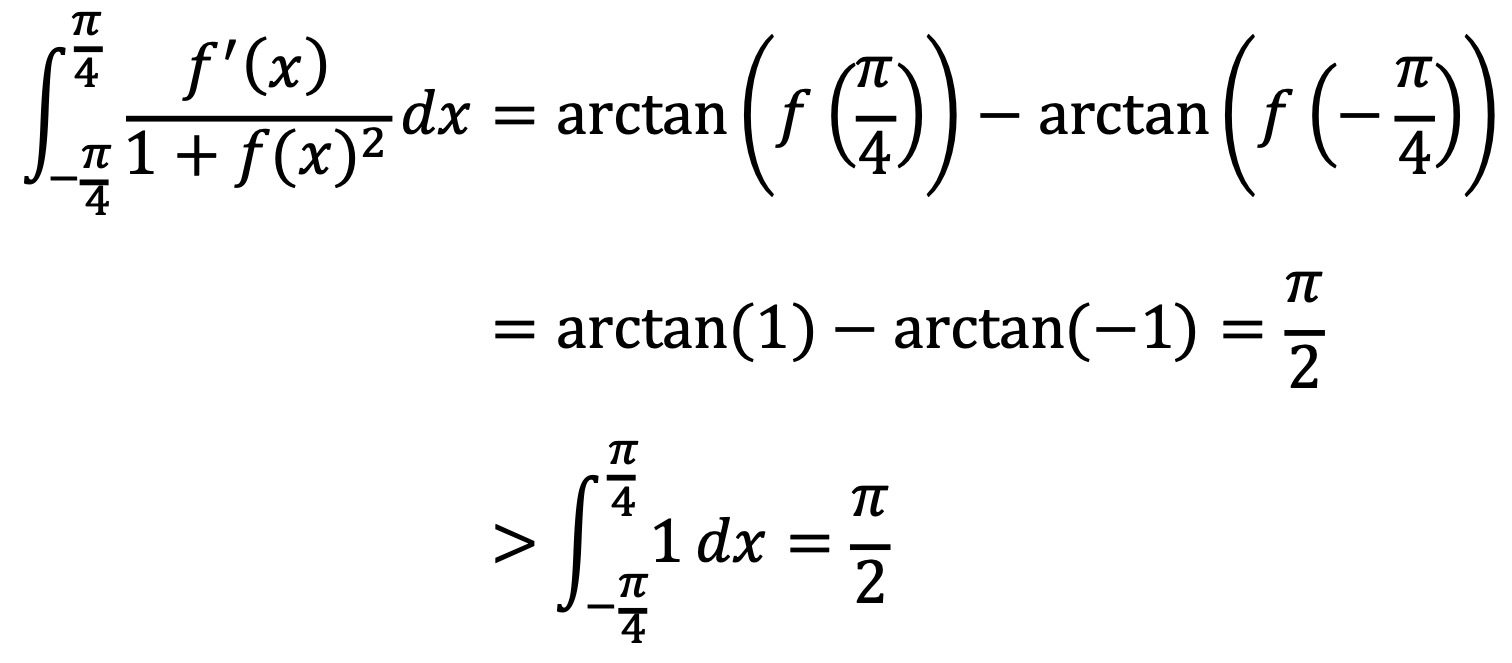
또한, f'(x) < -(1 + f(x)2)이라고 가정하면 다음과 같은 모순이 있다.
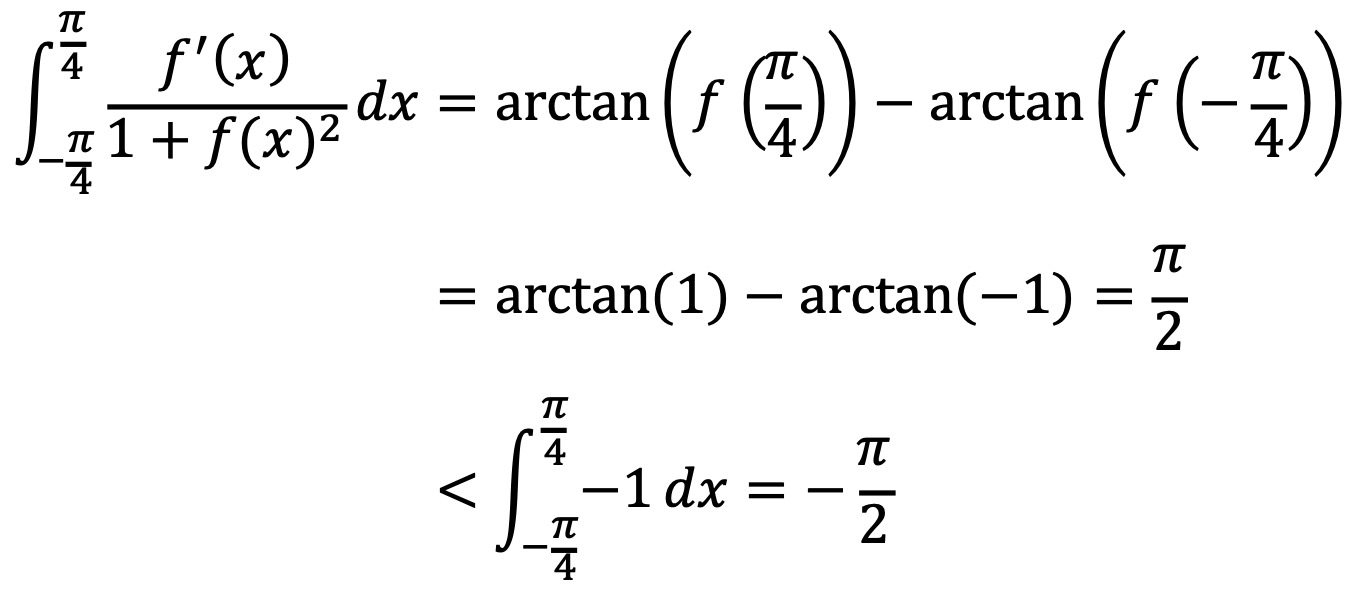
따라서 준 명제가 성립한다.
6. 양의 정수 m, n에 대하여 크기가 m × n인 실행렬 A가 주어져 있다.
⑴ 행렬 X = Im + AAT와 Y = In + ATA는 가역임을 보여라.
⑵ tr(X-1) - tr(Y-1)의 값을 구하여라.
(단, AT는 A의 전치행렬, 양의 정수 ℓ에 대하여 Iℓ은 크기가 ℓ × ℓ인 단위행렬)
Solution.
⑴
행렬 AAT는 대칭행렬이므로 AAT는 직교 대각화 가능하다. (∵ spectral theorem)
즉, AAT = PDPT = PDP-1
또한, 임의의 x ≠ 0에 대하여 xTAATx = |ATx|2 ≥ 0이므로 AAT는 양반정부호 행렬(positive semi-definite matrix)이다.
따라서 AAT의 모든 고유치 λ1, ···, λm은 0보다 크거나 같다.
X = Im + PDP-1 = P(Im + D)P-1이므로 X의 고유치는 (λX,1 + 1), ···, (λX,1 + 1) ≥ 1이다.
따라서 det(X) = (λX,1 + 1) × ··· × (λX,m + 1)이므로 X는 가역이다.
일반성을 잃지 않고, 행렬 Y도 가역이다.
⑵
AAT ∈ ℝm×m, ATA ∈ ℝn×n이 비록 행렬의 크기가 다르더라도 0이 아닌 고유치의 개수와 종류는 동일하다.
한편, tr(X-1) = tr(P(Im + D-1)P-1) = tr(Im + D-1) = ∑i (1 + λX,i)-1이 성립한다.
비슷하게, tr(Y-1) = ∑i (1 + λY,i)-1이 성립한다.
따라서 0이 아닌 고유치끼리는 서로 상쇄되어, tr(X-1) - tr(Y-1) = |m - n|이다.
7. 양의 실수 x1, x2, x3와 실수 a ∈ [-1/2, 1]에 대하여

라고 할 때, 다음 부등식을 증명하여라.

Solution.
젠센 부등식을 쓰자.

8. 양의 정수 n에 대하여 크기가 n × n인 실행렬 A, B가
A ≠ O, AB - BA = A
를 만족할 때, An = O이고 Bn ≠ O임을 보여라 (단, O는 영행렬).
Solution.
임의의 행렬 X ∈ V에 대하여 fB(X) = XB - BX로 정의하면, fB는 선형 사상이다.
AB - BA = A는 fB(A) = 1·A라는 형태이므로 고윳값 λ = 1에 대응하는 고유벡터가 A ≠ O라는 뜻이다.
fB(Ak) = AkB - BAk = kAk라고 가정하면,
fB(Ak+1) = (AkA)B - B(AkA) = Ak(BA + A) - BAk+1 = (BAk + kAk)A + Ak+1 - BAk+1 = (k+1)Ak+1
따라서 수학적 귀납법에 의해 fB(Ak) = kAk임을 확인할 수 있다.
만약 모든 k에 대하여 Ak ≠ O라고 한다면 선형함수 fB는 무수히 많은 고유치를 갖게 되므로 모순이다.
고유치는 최대 n개이므로 적당한 k ≤ n에 대하여 Ak = O가 성립한다.
그러므로 An = O가 성립한다.
한편, 임의의 양의 정수 k에 대하여

만약 Bn = O라면, BiABk-i에서 i ≥ n이거나 k - i ≥ n인 항은 전부 영행렬이 돼 버린다.
따라서 k가 충분히 크면 전체 합이 0이 돼 버려서 fBk(A) = O, k ≫ 1이 됨을 알 수 있다.
그런데 이미 fBk(A) = O임을 확인한 바 있으므로 이는 모순이다.
그러므로 Bn ≠ O가 성립한다.
입력: 2025.04.19 21:35
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 35회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2025.03.18 |
|---|---|
| 【대수경】 제 36회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.03.05 |
| 【대수경】 제 36회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2025.03.01 |
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.01.28 |
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 1 분야 (4) | 2025.01.06 |




최근댓글