제 36회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 36회 전국 대학생 수학경시대회
제 1 분야
2017년 (10:00 - 13:00)
1. 집합 S = {1, 2, ···, 2017}의 원소들은 성분으로 가지는 모든 n × n 행렬들의 집합을 T라고 하자. 다음 값을 계산하여라. (단, n은 2 이상의 양의 정수이다.)

Solution.
치환과 행렬식의 정의를 이해하자.

2. 임의의 실계수 다항식 f(x, y)는 (x + ay)k 꼴의 다항식들의 실계수 일차결합으로 표현됨을 보여라. (단, a는 임의의 실수, k는 0 이상의 정수이다.)
Solution.
이 문제는 임의의 2변수 실계수 다항식 f(x, y)에 대하여, 어떤 유한 개의 {(x + aiy)ki}와 실수 계수 {αi}를 골라서 다음을 보이는 것이다.

이제 다음을 만족하는 유한 개의 {ai}, {αi}가 언제나 존재하는지를 보이면 위 (준식)을 보일 수 있다.
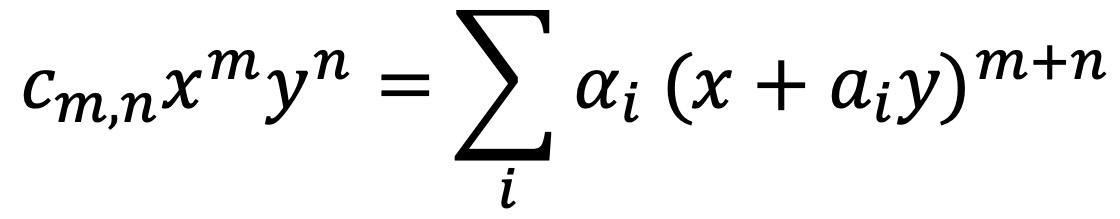
우변을 보면, (m+n)차 항이 여럿 나오는데 xmyn 항의 계수는 cm,n이고 xm+n-sys (단, s ≠ n) 항의 계수는 0이어야 한다.
따라서, α1, ···, αm+n+1에 대하여 다음과 같은 연립 1차 방정식의 해가 반드시 존재함을 보이면 충분하다.
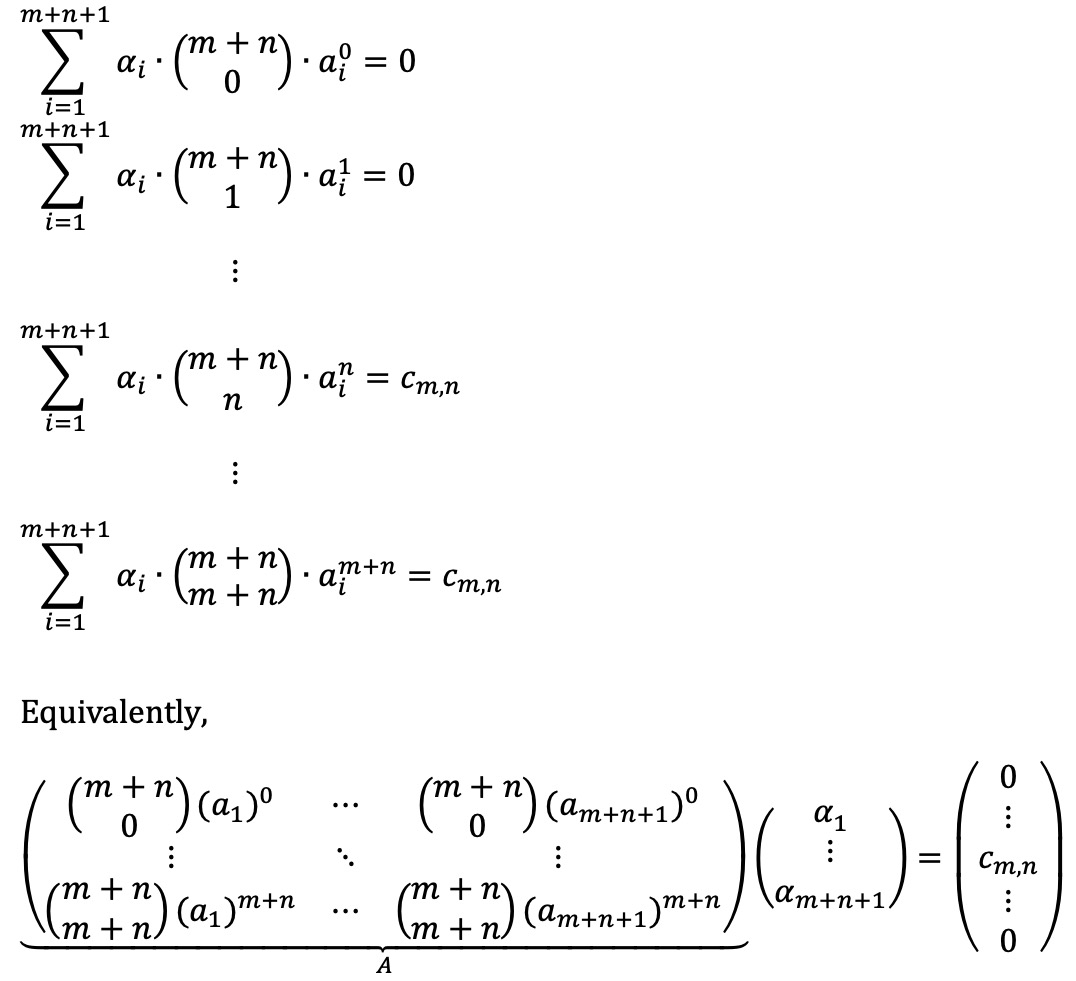
m+n = 1인 경우 해의 존재성을 보이는 건 아주 쉽다.
m+n > 1인 경우 am+n+1 ≫ a1, ···, am+n으로 설정하면 A에서 (am+n+1)m+n이 A의 다른 원소에 비해 매우 커진다.
따라서 det A ≠ 0이라고 할 수 있어 위 연립 방정식 시스템은 항상 해를 가진다.
그러므로 (준식)이 성립한다.
3. 수열 {an}이 a1 > 1이고 점화식 an+1 = 1 + n2 / an을 만족할 때, 극한 limn→∞ an / n을 구하시오.
Solution.
a1 > 1이므로 수학적 귀납법에 의해 a2k < 2k, a2k+1 > 2k+1임을 쉽게 증명할 수 있다.
따라서 an (단, n은 홀수)은 n이 충분히 클 때, nα, α ≥ 1의 스케일로 커진다. (단, α가 고정된 값이라고 단정하지 않음)
an(an+1 - 1) = n2으로부터 a2k × (a2k+1 - 1) = (2k+1)2을 얻을 수 있다.
따라서 k가 충분히 클 때 a2k+1이 nα의 스케일이라면 a2k는 nβ, β ≤ 1의 스케일로 커진다. (단, β가 고정된 값이라고 단정하지 않음)
이제 다음 식을 발견하자.
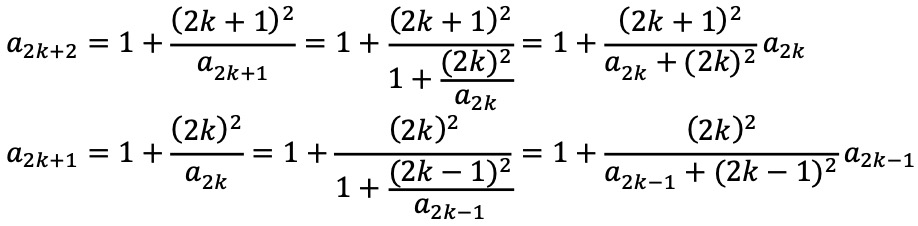
만약 k가 충분히 크면, a2k+2 ≃ 1 + a2k가 되어 β = 1을 반드시 암시한다.
따라서 an(an+1 - 1) = n2으로부터 α = 1을 알 수 있어서, a2k, a2k+1은 모두 k에 1차 비례해서 증가함을 알 수 있다.
더 나아가 k가 충분히 클 때 a2k+2 - a2k ≃ 1, a2k+1 - a2k-1 ≃ 1을 얻을 수 있어, 적어도 an / n은 홀짝성에 따라 다른 수렴값을 가지지 않는다.
따라서 (준식)의 극한값은 다음과 같다.

4. 실계수 3차 다항식 f(x) = x3 + ax2 + bx + c에 대하여 방정식 f(x) = 0의 세 근을 α, β, γ라 하자. 세 근 α, β, γ가 서로 다른 세 실수이기 위한 필요충분조건은 실대칭행렬
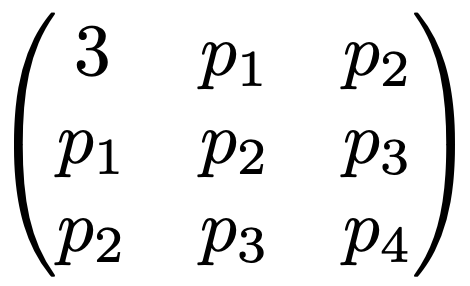
이 양의 정부호(positive definite)임을 보여라. (단, pi = αi + βi + γi이다.)
Solution.
증명 1. α, β, γ가 서로 다른 세 실근이면 행렬 M은 양의 정부호이다.
임의의 벡터 v = (v0, v1, v2) ≠ (0, 0, 0)에 대하여 다음이 성립한다.
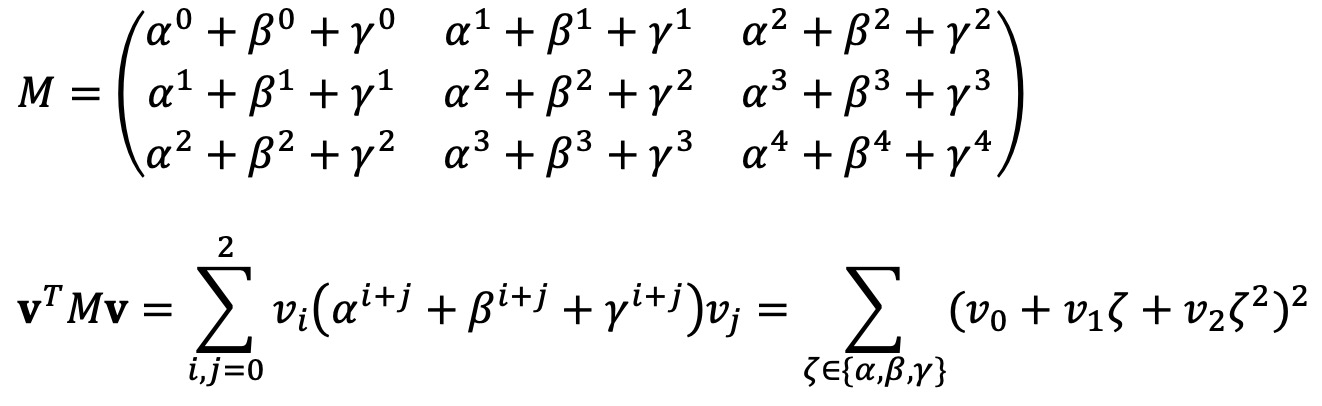
α, β, γ이 서로 다른 세 실근이라면 이 모두가 v0 + v1x + v2x2 = 0의 근이 될 수 없다.
따라서 vTMv > 0이 성립하므로 행렬 M은 양의 정부호이다.
증명 2. 행렬 M이 양의 정부호라면, α, β, γ는 서로 다른 세 실근을 이룬다.
Vandermonde 행렬식 개념을 검토하자.
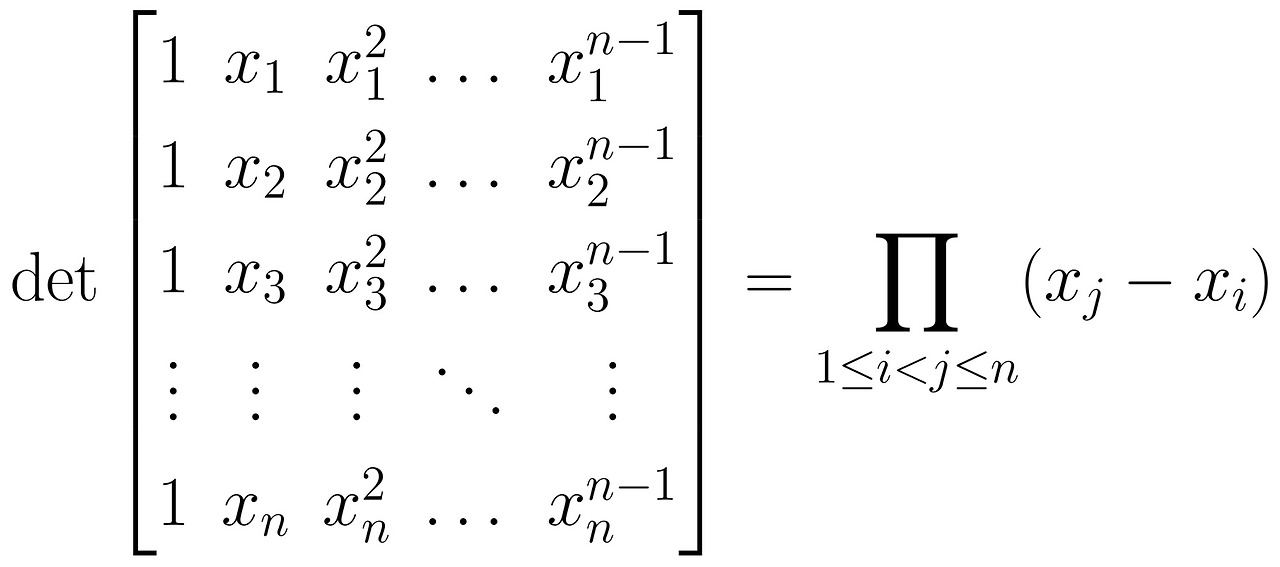
증명
주어진 행렬식은 다항식으로 표현된다.
예를 들어, xn을 보면 그 다항식은 xn에 대하여 n-1차 이하 다항식으로 표현된다.
특정 행벡터에서 다른 행벡터를 빼도 행렬식이 바뀌지 않는다는 사실을 주목하자.
n번째 행과 1번째 행의 차에서 행렬식이 (xn - x1)을 인수로 가짐을 알고, 비슷하게 (xn - x2), ···, (xn - xn-1)을 인수로 가진다.
그러므로 그 다항식은 xn에 대하여 (xn - x1) ··· (xn - xn-1)와 같이 표현된다.
이때, xnn-1이 포함된 항의 계수가 1임을 확인하자.
일반화를 잃지 않고 xn-1, xn-2, ···, x1에 대하여도 비슷하게 표현됨을 알 수 있어 위 식을 증명하였다.
행렬 M은 두 개의 Vandermonde 행렬의 곱으로 표현되고, M이 양의 정부호이므로 det(M) > 0이어야 한다.
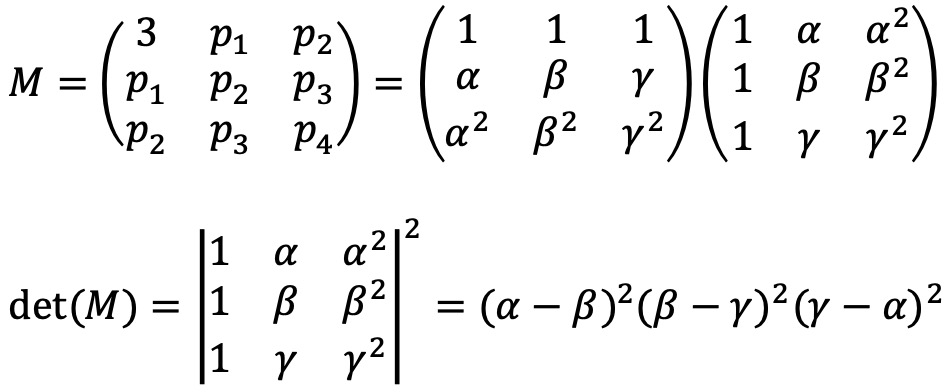
이제 주어진 방정식이 복소수 근을 갖는다고 가정하자.
삼차방정식은 적어도 한 개의 실근을 가지므로 일반성을 잃지 않고, α는 실수이며 β = a + bi, γ = a - bi라 하자.
그러면 다음과 같이 모순이 발생하므로, 주어진 방정식은 언제나 실근만을 갖는다.
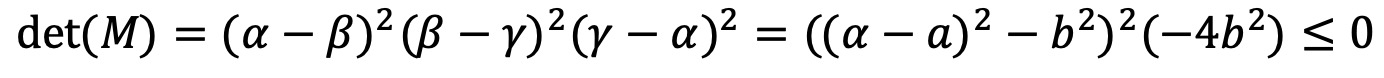
또한, 주어진 방정식이 중근을 갖는다면 vTMv = 0이 성립하는 v = (v0, v1, v2)을 찾을 수 있다. (증명 1 참고)
따라서, 세 근 α, β, γ가 서로 다른 세 실수이기 위한 필요충분조건은 M이 양의 정부호 행렬인 것이다.
5. 다음 극한을 계산하여라.
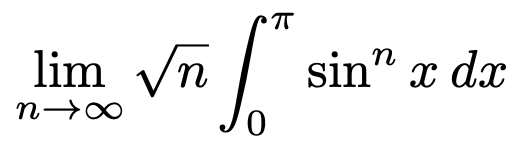
Solution.
부분분수법(integration by parts)에 의해 다음이 성립함을 확인하자.
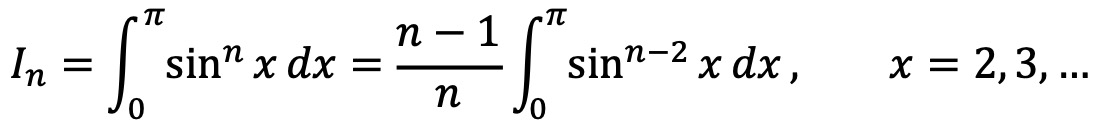
In은 n에 대하여 감소함수이므로 (준식)은 샌드위치 정리에 의해 n의 홀짝성에 따라 다른 수렴값을 가지지는 않는다.
따라서, 수렴값은 다음과 같다.

한편, 위 식에서는 엄밀하게 수렴성을 보이지는 않았지만, In-2 > In-1 > In > In+1 > In+2 이므로 √(In-2·In-1) > In > √(In+1·In+2)와 같이 식을 구성할 수 있어서 수렴값뿐만 아니라 수렴성도 같이 보여주는 식으로 식을 다시 구성해볼 수도 있다.
6. 양의 정수 n에 대하여 n × n 실행렬 A는 모든 성분이 1인 행렬 J에 대하여 다음을 만족한다.
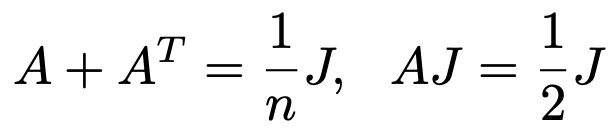
모든 양의 홀수 m에 대하여 Am - I가 가역행렬임을 보여라. (단, AT는 A의 전치행렬이다.)
Solution.
공식 풀이를 참고하였다.
우선 A2 = A(-AT + (1/n)J) = -AAT + (1/2n)J이므로 A2은 대칭행렬이다.
이제 홀수 m에 대하여 Am + (Am)T = μmJ가 성립한다면 수학적 귀납법에 의해 다음이 성립한다.
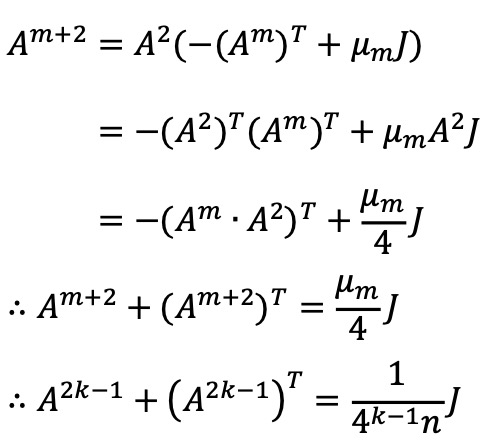
(A2k-1 - I)x = 0인 x는 다음을 만족한다.
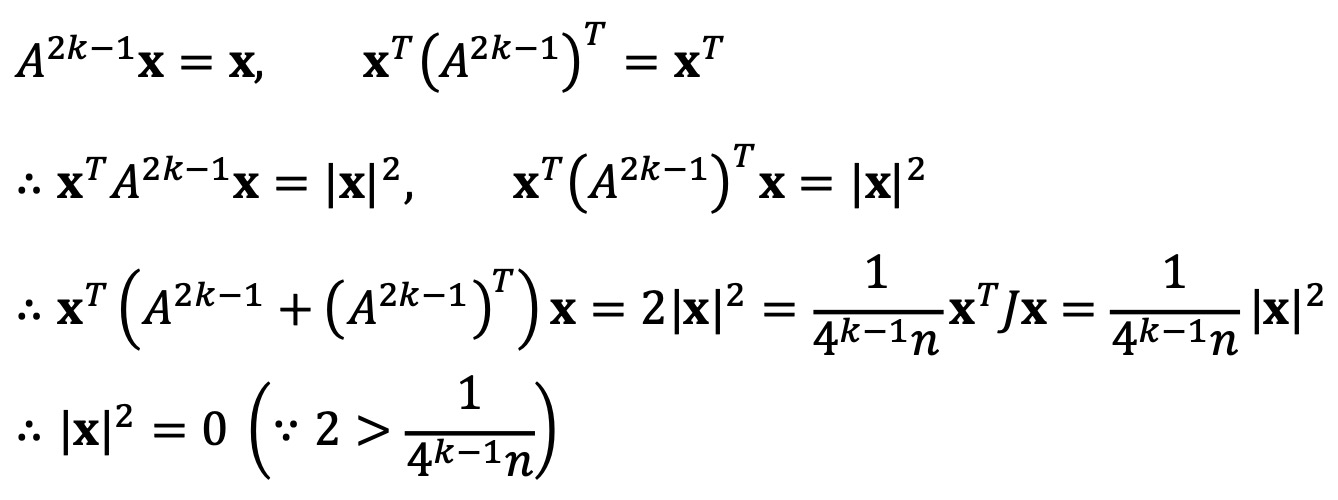
따라서 dim(Ker(A2k-1)) = 0이므로 dim(Im(A2k-1)) = n, 즉 A2k-1은 가역행렬이다.
7. 수열 {an}은 모든 항이 양수인 감소하는 수열이고, 0 < θ < π / 2이다. 다음이 성립함을 보여라.
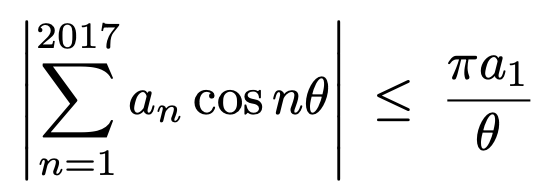
Solution.
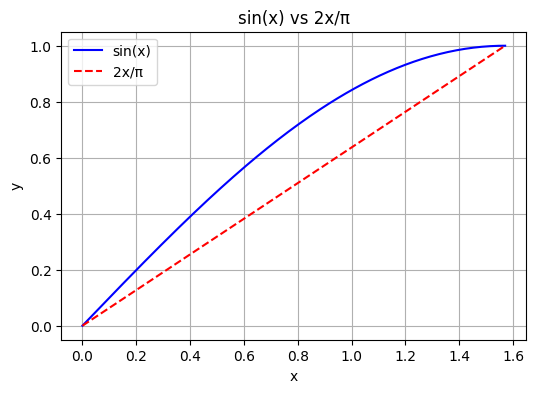
위 그림과 같이 0 < x < π / 2에서 sin x ≥ 2x / π임을 이용하면, (준식)을 유도할 수 있다.
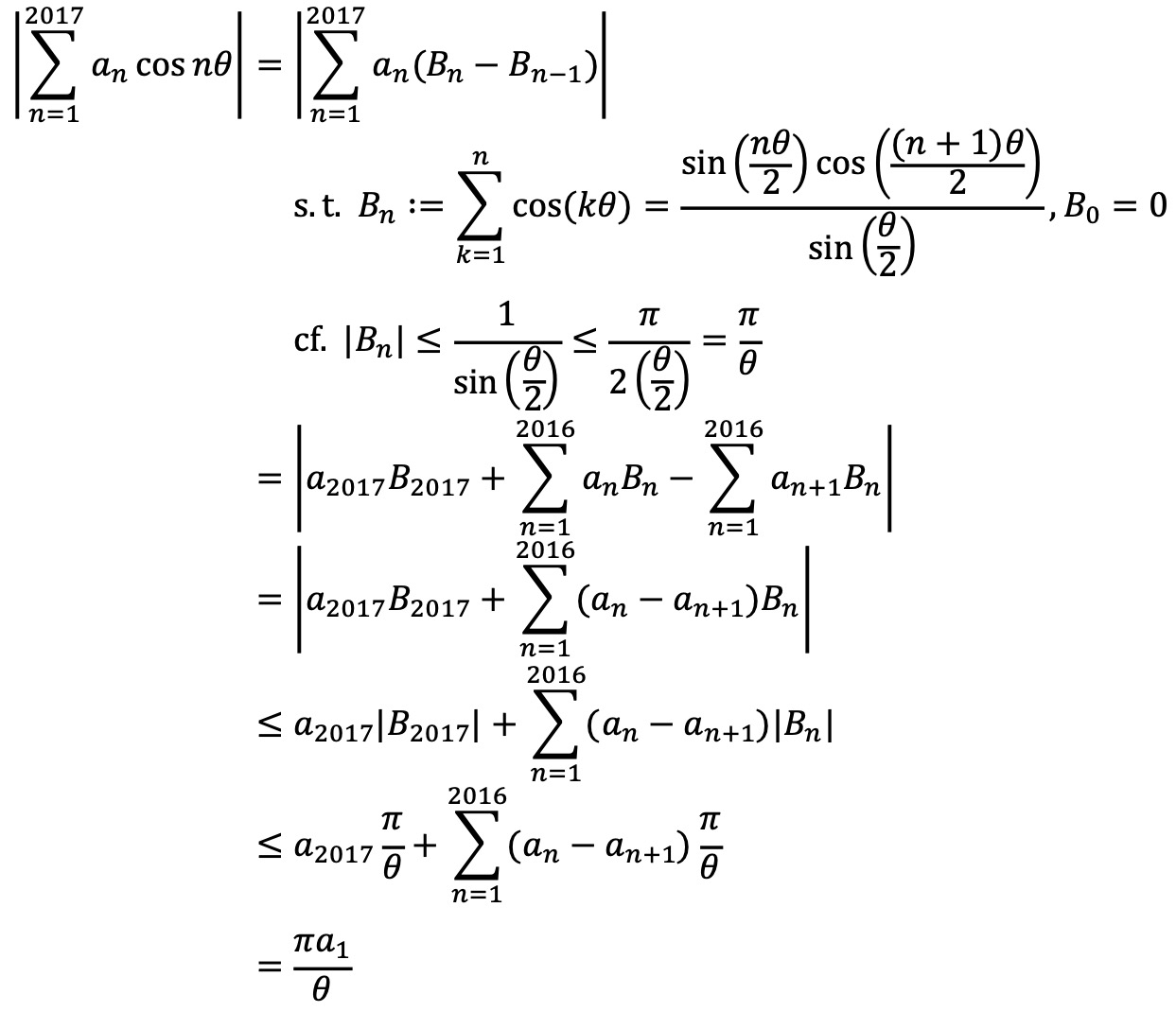
참고로, Bn의 일반항을 구하는 방법은 두 가지가 있다.
방법 1. 복소수 지수함수의 등비수열

방법 2. 수학적 귀납법
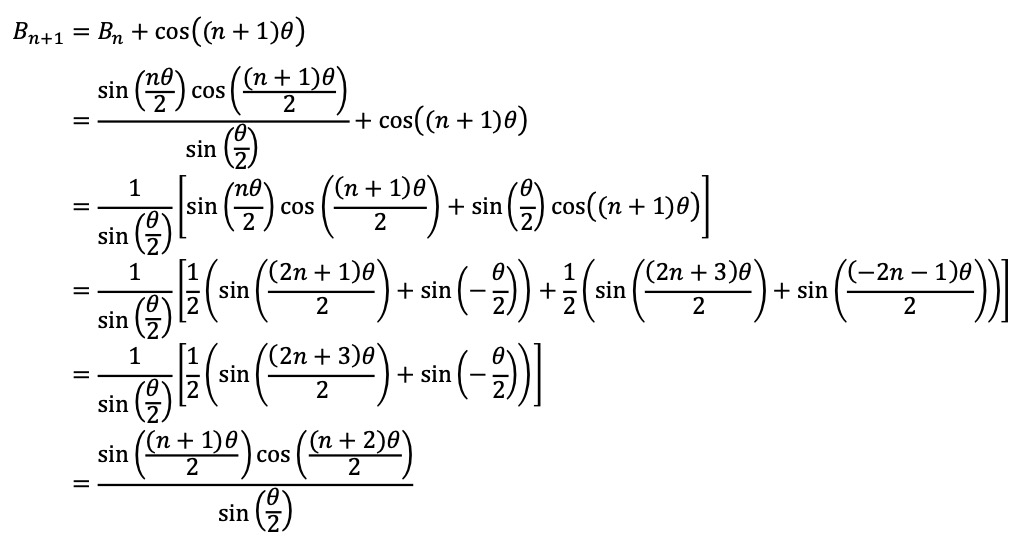
8. 다음 미분방정식의 해를 u(t)라고 하자.
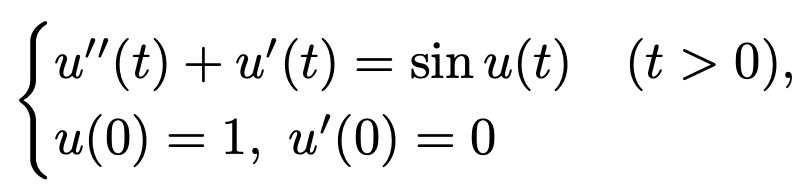
⑴ 함수 u(t)와 u'(t)가 t > 0인 범위에서 유계임을 보여라.
⑵ 극한 limt→∞ u(t)를 구하여라.
Solution. (저의 풀이)
⑴
u(t)가 유계임을 다음과 같이 보일 수 있다.
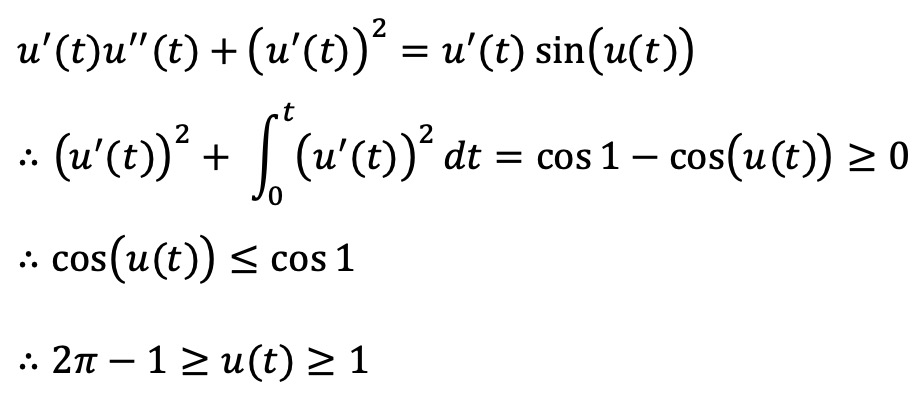
또한, u'(t)가 유계임을 다음과 같이 보일 수 있다.
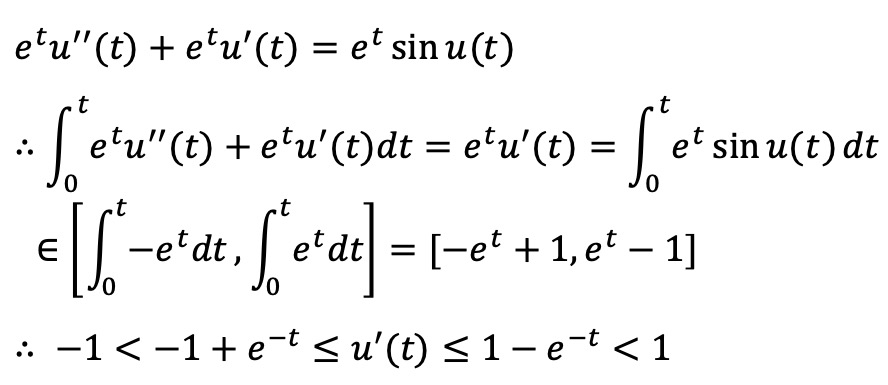
⑵
이 시스템은 F (외력) = ma = -kv (저항력) + sin u (포텐셜 에너지)와 같은 진동계이다.
이 물리 시스템은 sin u(t) > 0인 경우 물체를 앞으로 이동시키고 sin u(t) < 0인 경우 뒤로 이동시키는 게 잘 알려져 있다.
더 자세한 설명을 위해 Jacobi Elliptic Function을 참고하자.
직관적으로 보면, 시스템이 주기 함수로 구성되지 않아 물체의 위치 u가 특정한 주기 T로 원래 초기 위치로 돌아오지 않을 가능성이 높다.
실제로, 주기성을 얻으려면 특정한 파라미터 조합을 맞춰야 하므로, 일반적으로 주기성이 없다고 가정할 수 있다.
따라서, u(t)는 유계이므로 물체가 한 번 앞으로 갔다가 뒤로 돌아오는 진동을 하는데, 두 번째 시작 위치가 처음 시작 위치보다 앞에 온다.
⑴의 풀이에서 주목할 만한 부분은 다음과 같다.
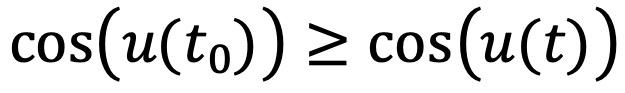
일단 두 번째 시작 위치가 처음 시작 위치보다 앞에 있으면, u(t)의 범위는 [두 번째 시작 위치 ~ 2π - 두 번째 시작 위치]로 제한된다.
이렇게 한 주기를 끝낼때마다 u(t)가 포함될 수 있는 구간은 점점 좁아지며, 결국 π를 중심으로 수렴해간다.
엄밀하게는, 각 주기에서 u(t)의 시작 위치는 증가수열이며, 완비성 공리에 의해 증가수열이 유계이면 그 수열은 수렴한다.
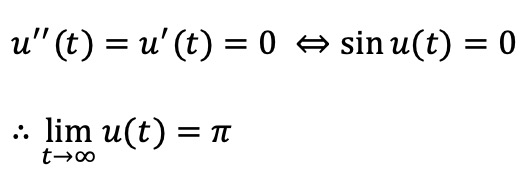
Solution. (공식 풀이)
⑴
우선 v(t) := u'(t)로 두자. 그러면 (u(0), v(0)) = (1, 0)이고 다음이 성립한다.
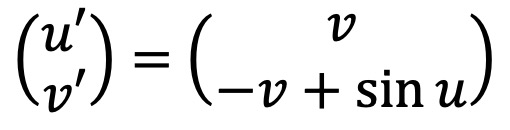
따라서 -et ≤ |et v(t)|' = et sin u(t) ≤ et 임을 알 수 있다.
이를 적분하여 |v| ≤ 1 - e-t ≤ 1 를 얻는다.
또한 w(t) := 2 cos u(t) + (v(t))2 으로 두면 w' = -2u' sin u + 2vv' = 2v sin u + 2v(-v + sin u) = -2v2 이므로, w(t)는 감소함수이다.
이로부터 cos u(t) ≤ cos u(t) + (v(t))2 / 2 ≤ cos u(0) + (v(0))2 / 2 = cos 1 을 알 수 있다.
따라서 u(t)의 연속성을 이용하여, 모든 t ≥ 0에 대하여 1 ≤ u(t) ≤ 2π-1 임을 얻는다.
⑵
함수 w(t)는 감소함수이면서 w(t) ≥ -2이므로, limt→∞ w(t) = β가 존재하고, 다음이 성립한다.
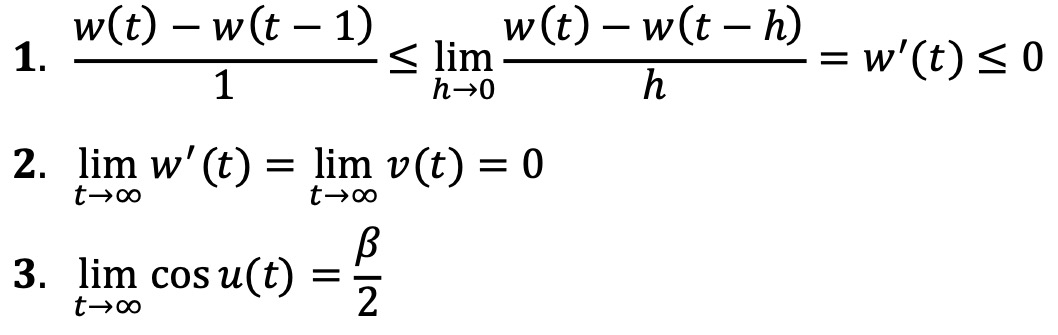
이때, β > 2라고 가정하자.
그러면 임의의 ε > 0에 대하여 어떤 t0가 존재하여, t > t0인 모든 t에 대하여 cos u(t) > β / 2 - ε, |v(t)| < ε이다.
여기에서 β / 2 - ε > -1이 되도록 충분히 작다고 가정하면, 다음과 같이 두 가지 경우가 생긴다.
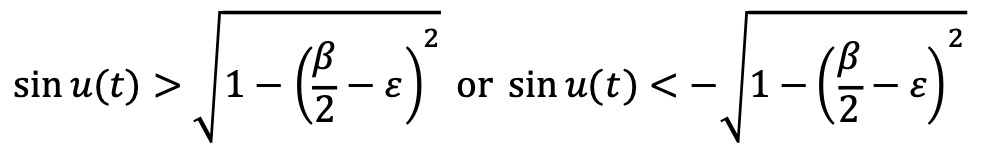
만약 첫 번째 경우이면, 충분히 작은 ε > 0에 대하여
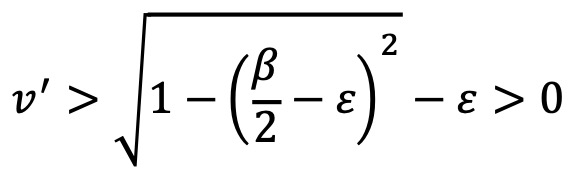
이고, 이는 v가 유계라는 사실에 모순이다.
두 번째 경우에도 마찬가지로 모순을 얻는다.
따라서, limt→∞ cos u(t) = -1이고, limt→∞ u(t) = π이다.
입력: 2025.02.28 09:36
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 35회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2025.03.18 |
|---|---|
| 【대수경】 제 36회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.03.05 |
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.01.28 |
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 1 분야 (4) | 2025.01.06 |
| 【대수경】 제 38회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.12.29 |




최근댓글