제 37회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 37회 전국 대학생 수학경시대회
제 2 분야
2018년 11월 17일 (10:00 - 13:00)
1. 좌표평면 위의 두 직선 y = (1 - h)x와 y = (1 + h)x 사이의 각을 θ(h)라 하자. (단, θ(h) ∈ [0, π/2].) 극한 limh→0+ θ(h)/h 의 값을 구하여라.
Solution.
v1 = (1, 1-h), v2 = (1, 1+h)로 두면 cos θ(h)는 다음과 같다.

따라서 로피탈 정리(L'Hospital's theorem)에 의해 준식을 다음과 같이 나타낼 수 있다.

2. 다음 미분방정식의 해를 구하여라.

Solution.
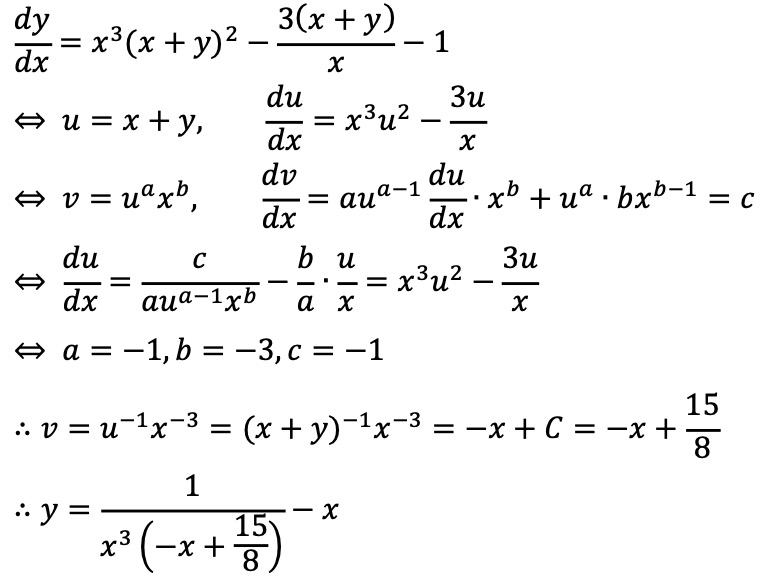
3. 크기가 2 × 2인 실행렬들로 이루어진 실벡터공간을 V라 하자. 행렬 A ∈ V가 tr(A) = 3, tr(A2) = 5를 만족할 때, V에서 정의되는 선형사상 T(B) = AB + BA에 대하여 tr(T3)을 구하여라.
Solution.
공식 풀이를 참고하였다.
tr(AB) = tr(BA), tr(An) = tr(P-1DnP) = tr(P-1PDn) = tr(Dn) = ∑i λin임을 주목하자.
(주석 : 위 식은 대각화 가능성과 별개로 성립하는 것처럼 보인다.)
A의 두 고유치 λ1 + λ2는 tr(A) = λ1 + λ2 = 3, tr(A2) = λ12 + λ22 = 5로부터 각각 1, 2임을 알 수 있다.
A는 서로 다른 고유값을 가지므로 A는 대각화 가능하다.
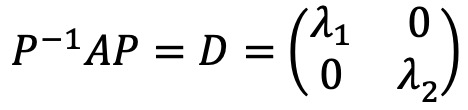
기본행렬 Eij (i, j = 1, 2)에 대하여, X = Xij = PEijP-1이라 두면, 다음이 성립한다.
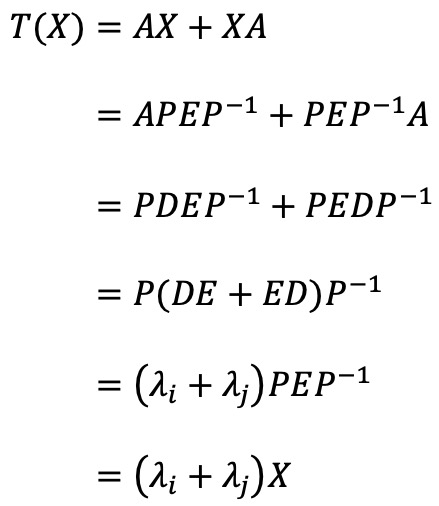
그러므로 선형사상 T도 대각화 가능하고 고유치는 λi + λj (i, j = 1, 2)이다: 2, 3, 3, 4.
결과적으로 tr(T3) = 23 + 33 + 33 + 43 = 126이다.
4. 지구 북반구 위의 두 지점 A와 B의 위치는 각각 (위도 α, 경도 0)과 (위도 β, 경도 π/2)이다. (단, 지구는 구라고 가정하고 각도의 단위는 라디안이며, 0 < α, β < π/2이다.) 지점 A에서 지점 B까지 두 점을 지나는 지표면 위의 대원을 따라 북반구 위를 이동할 때, 가장 높은 위도를 지나는 순간의 경도를 γ라 하자. 이때, tan γ를 α와 β에 관한 식으로 표현하여라.
Solution.
공식 풀이를 참고하였다.
지구 위에 있는 임의의 점은 (r cos ϕ cos θ, r cos ϕ sin θ, r sin ϕ), 0 ≤ θ < 2π, -π/2 ≤ ϕ ≤ π/2로 나타낼 수 있다. (단, ϕ는 위도, θ는 경도)
이때 A = (r cos α, 0, r sin α), B = (0, r cos β, r sin β)이다.
따라서 A와 B를 지나는 대원의 법선 벡터는 다음과 같다.
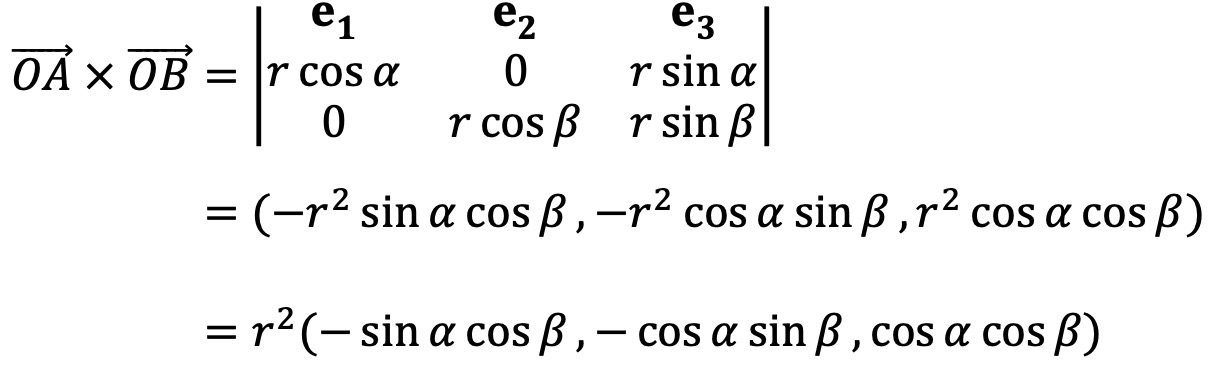
따라서, 대원 상에 있는 점은 다음과 같이 정의된다.
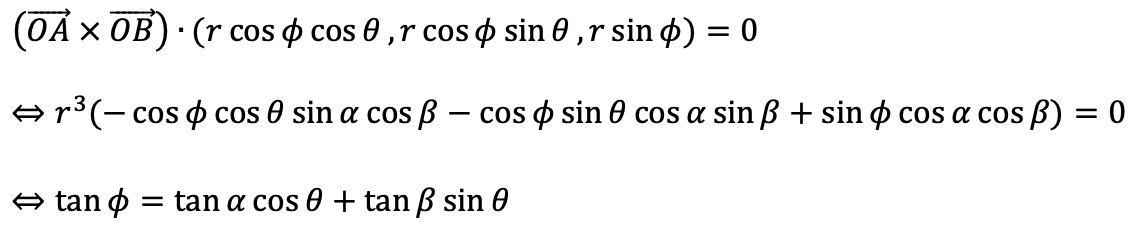
적당한 매개변수 t에 대하여 위 식을 tan ϕ(t) = tan α cos θ(t) + tan β sin θ(t) 라고 둘 수 있다.
이 대원에서 가장 높은 위도를 지나는 순간은 다음과 같다.
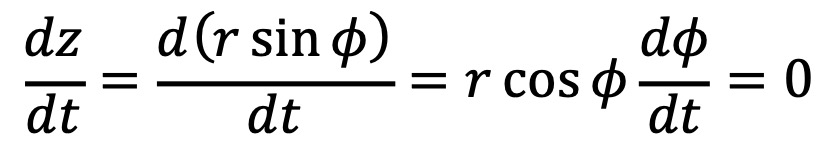
그러므로 다음 식을 얻을 수 있다.
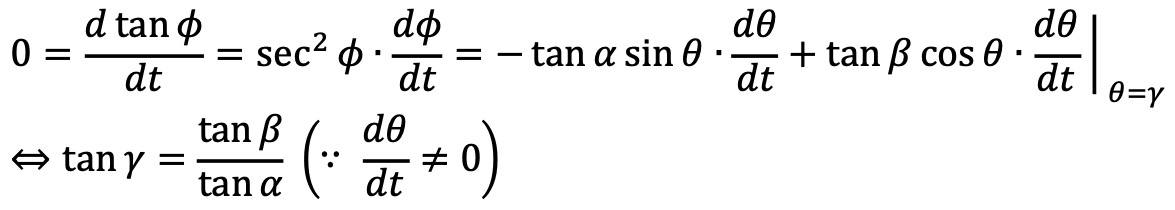
5. 정수 1, 2, ···, n을 재배열하여 얻어지는 임의의 두 순열 (α1, ···, αn)과 (β1, ···, βn)에 대하여 n × n 행렬 A = (aij)는 aij = (1 + αiβj)n-1로 정의된다. 행렬식 det(A)가 취할 수 있는 값을 모두 구하여라. (단, n ≥ 2)
Solution.
주어진 행렬에서 임의의 두 열 혹은 두 행을 서로 뒤바꾸면 행렬식의 부호가 바뀌고 크기는 동일하다.
적절히 주어진 행렬의 열과 행의 순서를 바꾸면, αi = i, βj = j가 되도록 할 수 있다.
따라서, A0 = ( (1 + i × j)n-1 )인 행렬이 있을 때, det(A)가 취할 수 있는 값은 ± det(A0)이다.
한편, Vandermonde 행렬식 개념을 검토하자.
증명
주어진 행렬식은 다항식으로 표현된다.
예를 들어, xn을 보면 그 다항식은 xn에 대하여 n-1차 이하 다항식으로 표현된다.
특정 행벡터에서 다른 행벡터를 빼도 행렬식이 바뀌지 않는다는 사실을 주목하자.
n번째 행과 1번째 행의 차에서 행렬식이 (xn - x1)을 인수로 가짐을 알고, 비슷하게 (xn - x2), ···, (xn - xn-1)을 인수로 가진다.
그러므로 그 다항식은 xn에 대하여 (xn - x1) ··· (xn - xn-1)와 같이 표현된다.
이때, xnn-1이 포함된 항의 계수가 1임을 확인하자.
일반화를 잃지 않고 xn-1, xn-2, ···, x1에 대하여도 비슷하게 표현됨을 알 수 있어 위 식을 증명하였다.
따라서 det(A0)은 다음과 같다.
그러므로 det(A)가 취할 수 있는 값은 ± ( (n-1)! )n이다.
6. 다음 급수의 값을 구하여라.
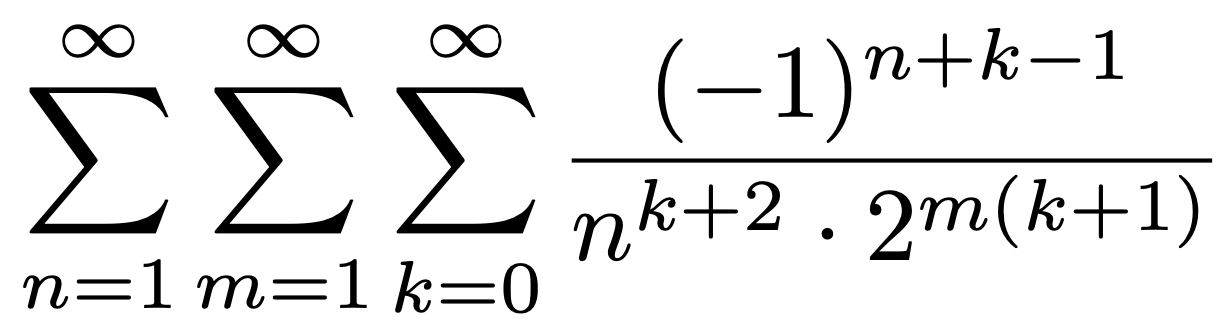
Solution.
다음은 공식 풀이를 참고하여 작성한 풀이이다.
수렴성은 쉽게 보일 수 있으므로 수렴값에 집중하자.

ln (1+x) 및 ln (1-x)의 테일러 급수를 이용하면 ∞ - ∞ 같이 되어 2 - ln 2 같이 나올 수 있으므로 유의하자.
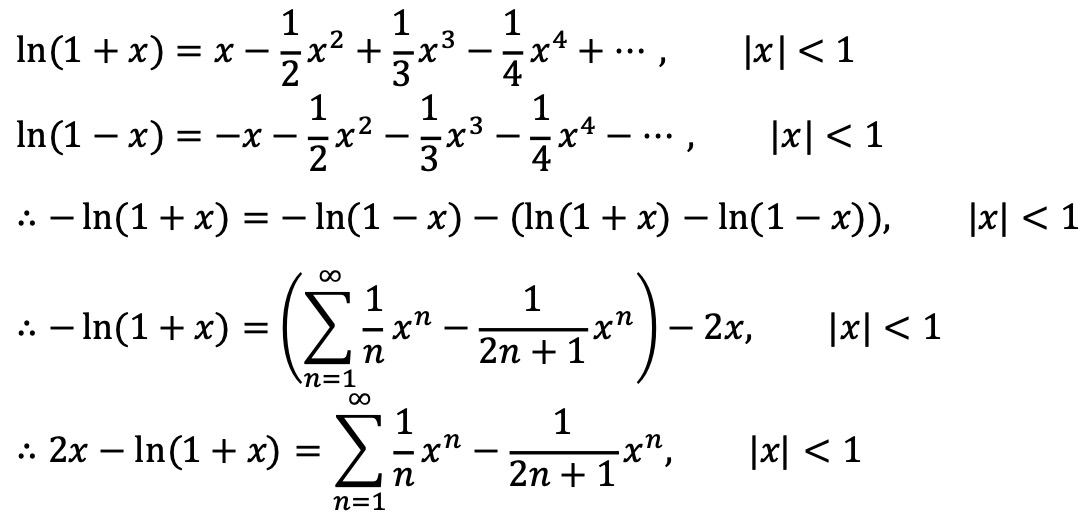
다른 풀이도 시도하였으나 결국 풀리지 않았다. (ChatGPT 및 Wolfram Alpha도 풀지 못했다.)
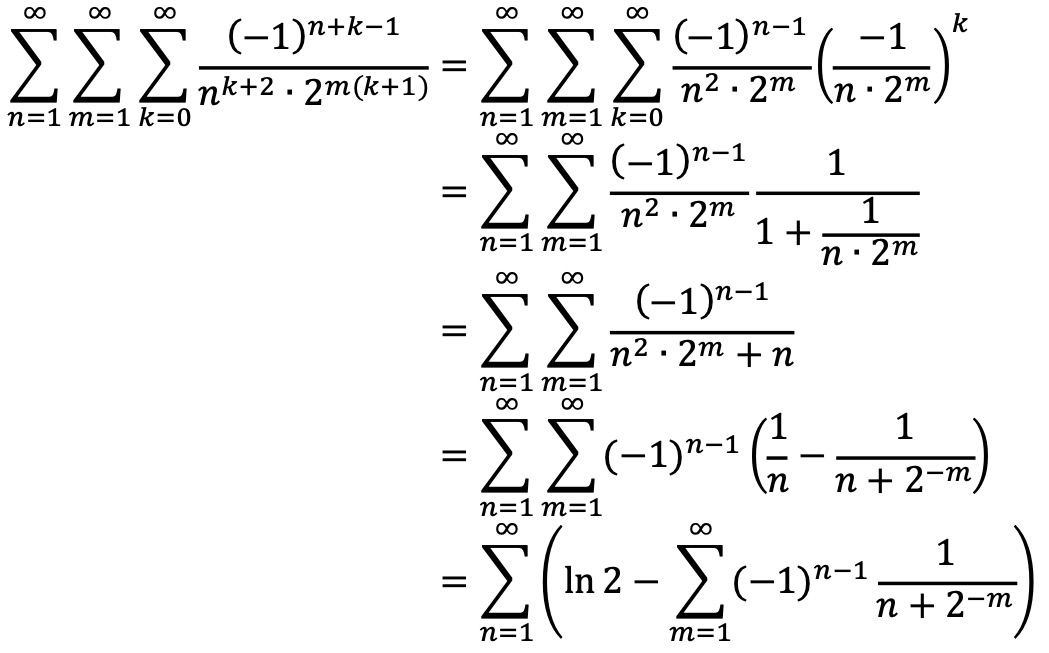
7. 수열 {an}은 임의의 양의 정수 n에 대하여 다음과 같이 정의된다.
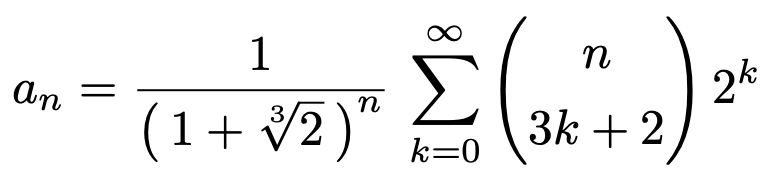
극한 limn→∞ an의 값을 구하여라. 단, 3k + 2 > n이면 nC3k+2 = 0이다.
Solution.
복소 3차 근원(roots of unity)을 이용하자. ω = exp(2πi / 3)이라고 정의하면, 다음 식을 찾을 수 있다.
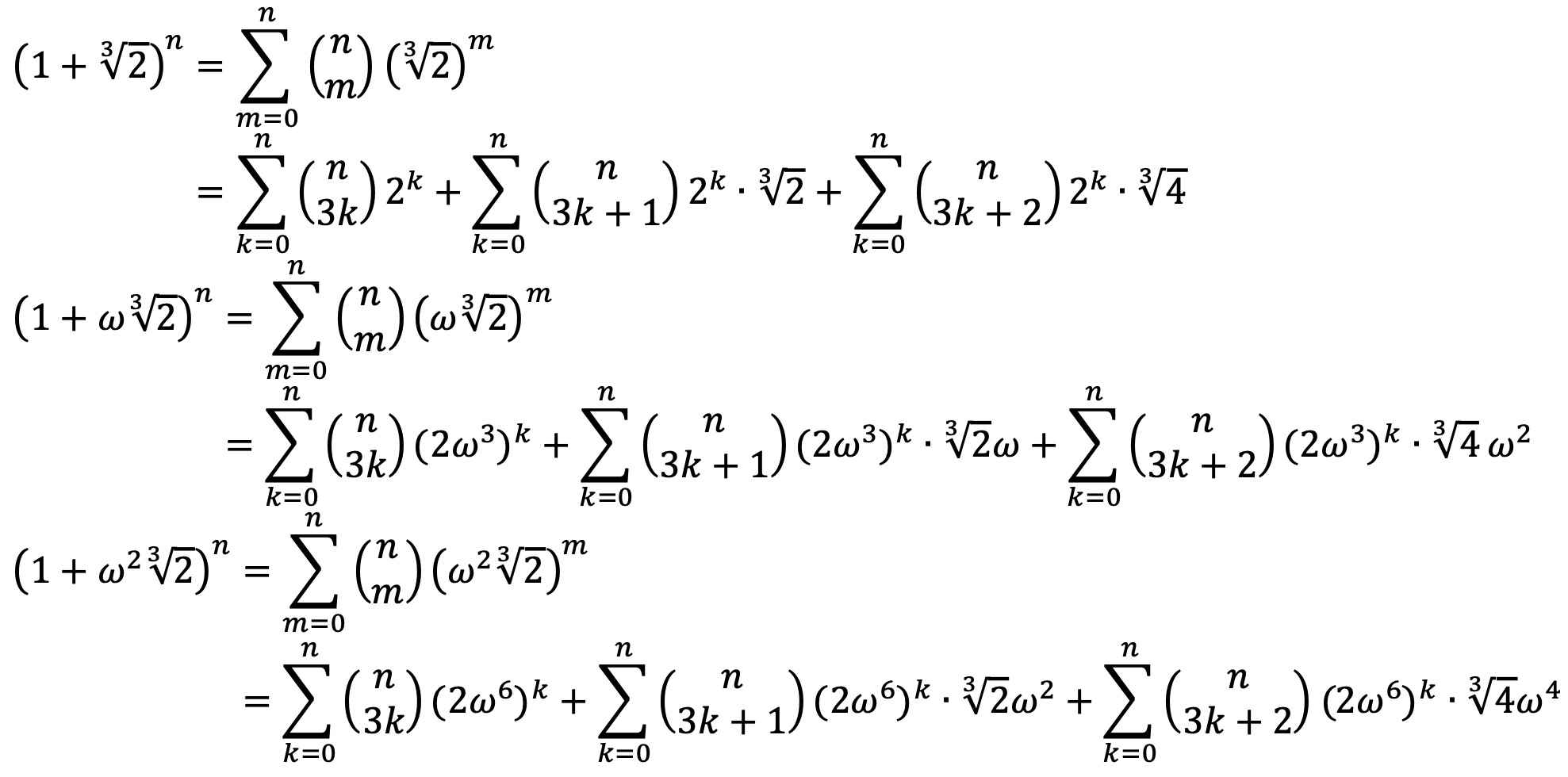
이때, ω에 관한 다음 성질을 확인하자.
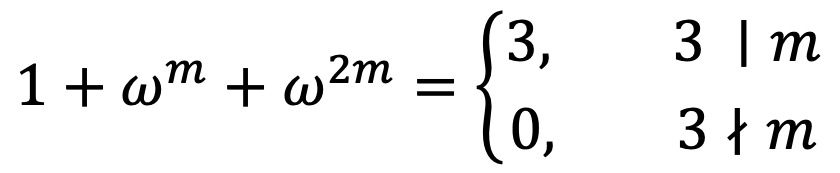
그러므로 nC3k+2 항을 남기기 위해 적절히 ω, ω2을 곱하여 더해주면 다음을 얻을 수 있다.
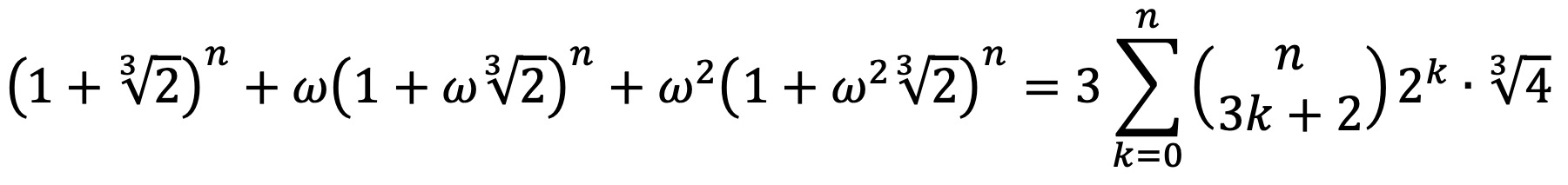
그런데 삼각부등식에 의해 다음이 성립한다.
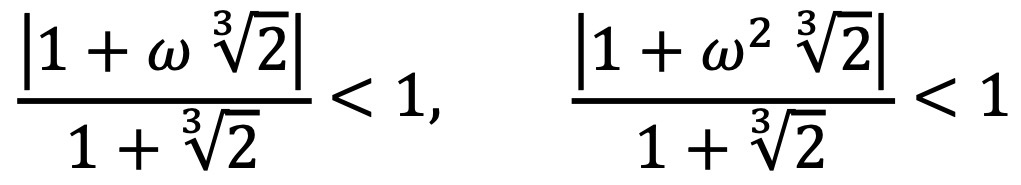
그러므로 (준식)은 다음과 같다.
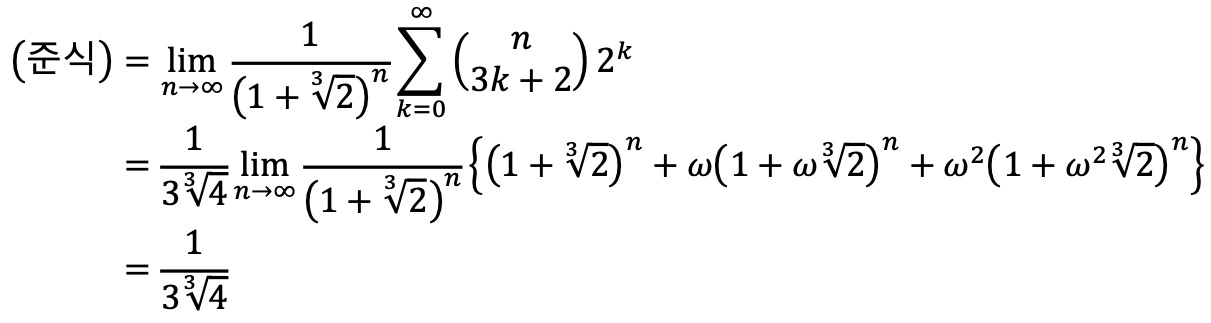
8. 두 번 미분가능한 함수 f : ℝ → (0, ∞)가 다음 조건을 만족한다.
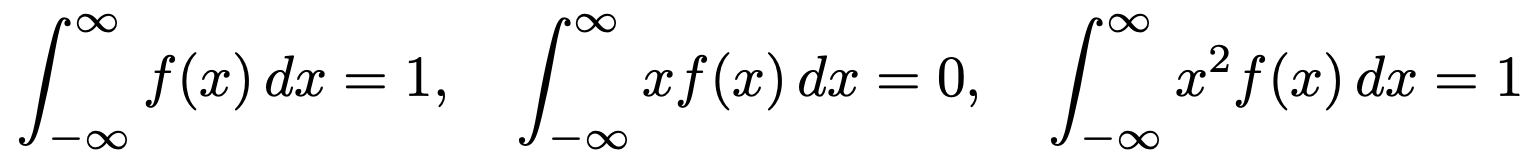
다음 부등식이 성립함을 보이고, 등호가 성립하도록 하는 함수 f를 모두 구하여라.
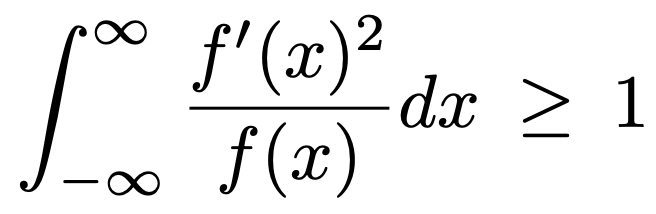
Solution.
∫x=-∞ to ∞ x f(x) dx < ∞이므로, limx→-∞ x f(x) = limx→∞ x f(x) = 0이 성립한다.
이제 다음 코시-슈바르츠 부등식이 성립함을 확인하자.
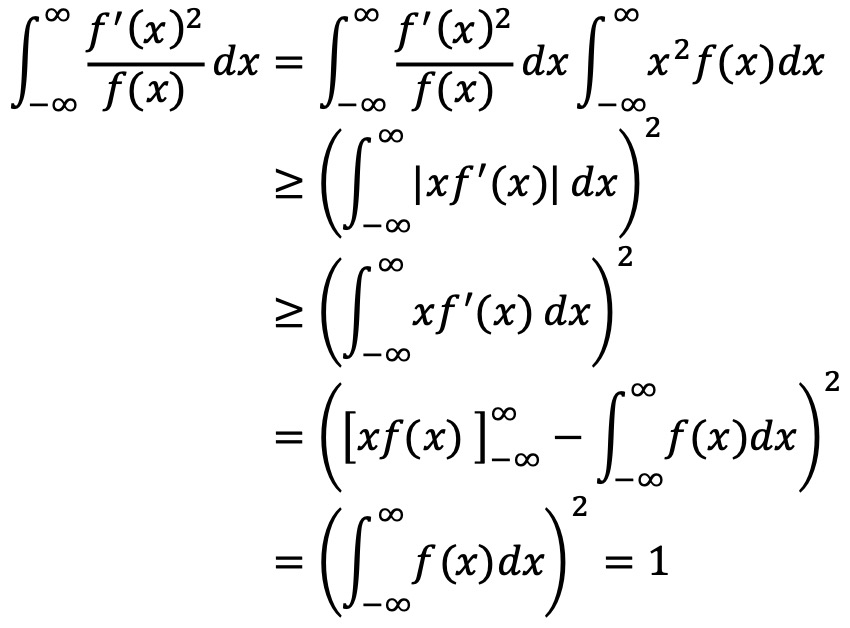
등호조건이 성립하려면 다음과 같다.
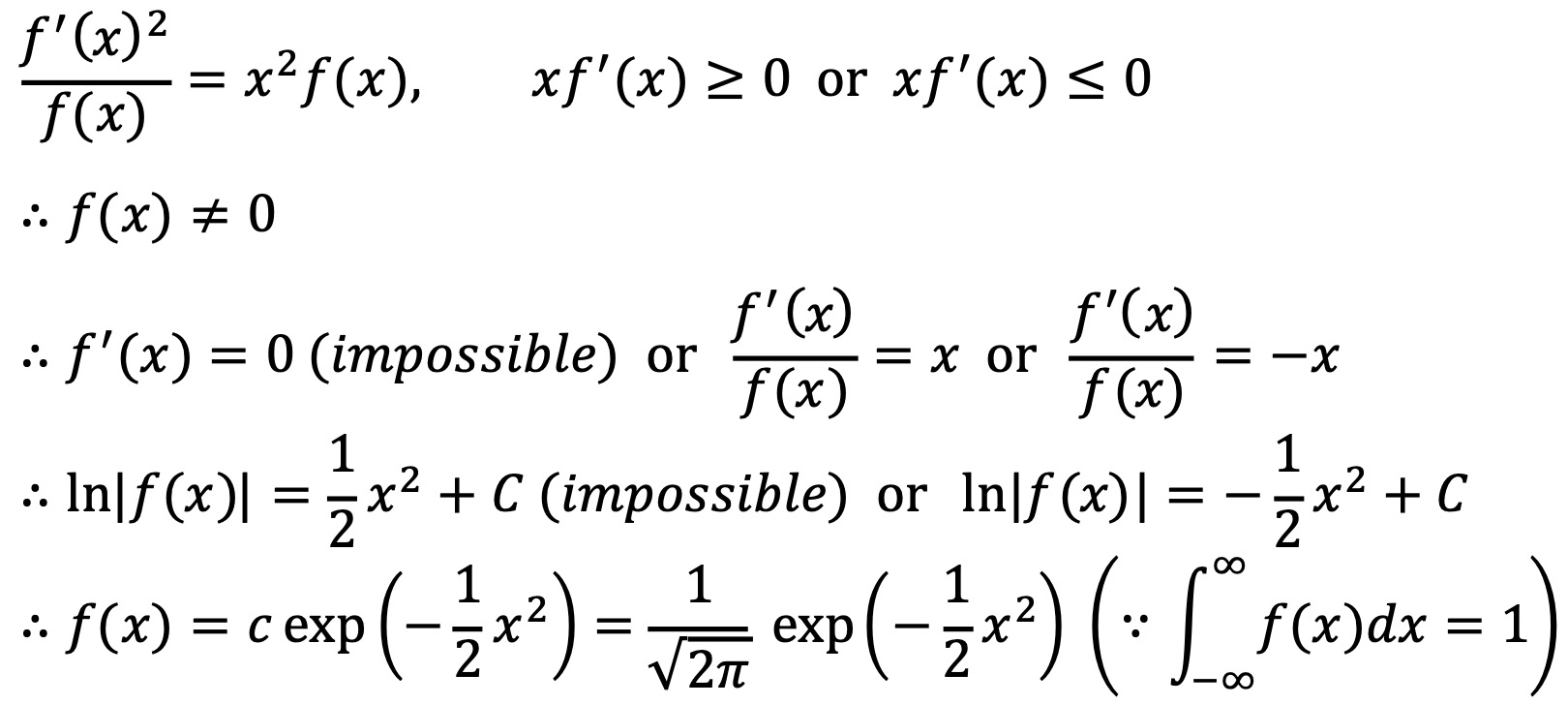
입력: 2025.01.27 10:41
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 1 분야 (4) | 2025.01.06 |
|---|---|
| 【대수경】 제 38회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.12.29 |
| 【대수경】 제 38회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.12.29 |
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.12.08 |
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2024.12.07 |







최근댓글