제 38회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 38회 전국 대학생 수학경시대회
제 1 분야
2019년 11월 9일 (10:00 - 13:00)
1. 다음 행렬 A에 대하여 rank(A)를 구하여라.

Solution.
det(A) = 0이므로 rank(A) < 3이다.

한편,

이므로 (2019, 2020, 2021)T와 (2020, 2021, 2022)T는 일차독립이다.
그러므로, rank(A) ≥ 2이다.
따라서 rank(A) = 2이다.
2. 행렬 A와 B가 다음과 같이 주어져 있다.

이 때, 입체 V = {x ∈ ℝ3 : x · Ax ≤ 1 < x · Bx }의 부피를 구하여라.
Solution.
이차형식을 풀어쓰면, x · Ax = 2x12 + 2x22 + 2x1x2 + 3x32, x · Bx = 4x12 + 4x22 + 4x1x2 + 12x32을 얻는다.
(x, y)을 (x1, x2)을 -45° 회전시킨 점이라고 할 때, x1 = (x - y) / √2, x2 = (x + y) / √2를 얻을 수 있다.
이때 x3 = z라고 하면, x · Ax = 3x2 + y2 + 3z2, x · Bx = 6x2 + 2y2 + 12z2을 얻는다.
회전변환은 입체의 부피를 보존하므로 V' = {(x, y, z) : 3x2 + y2 + 3z2 ≤ 1 < 6x2 + 2y2 + 12z2}을 고려하는 것으로 충분하다.
두 타원체는 서로 교점이 없으므로 주어진 영역의 부피를 구하는 것은 두 타원체의 사이 공간의 부피를 구하면 된다.
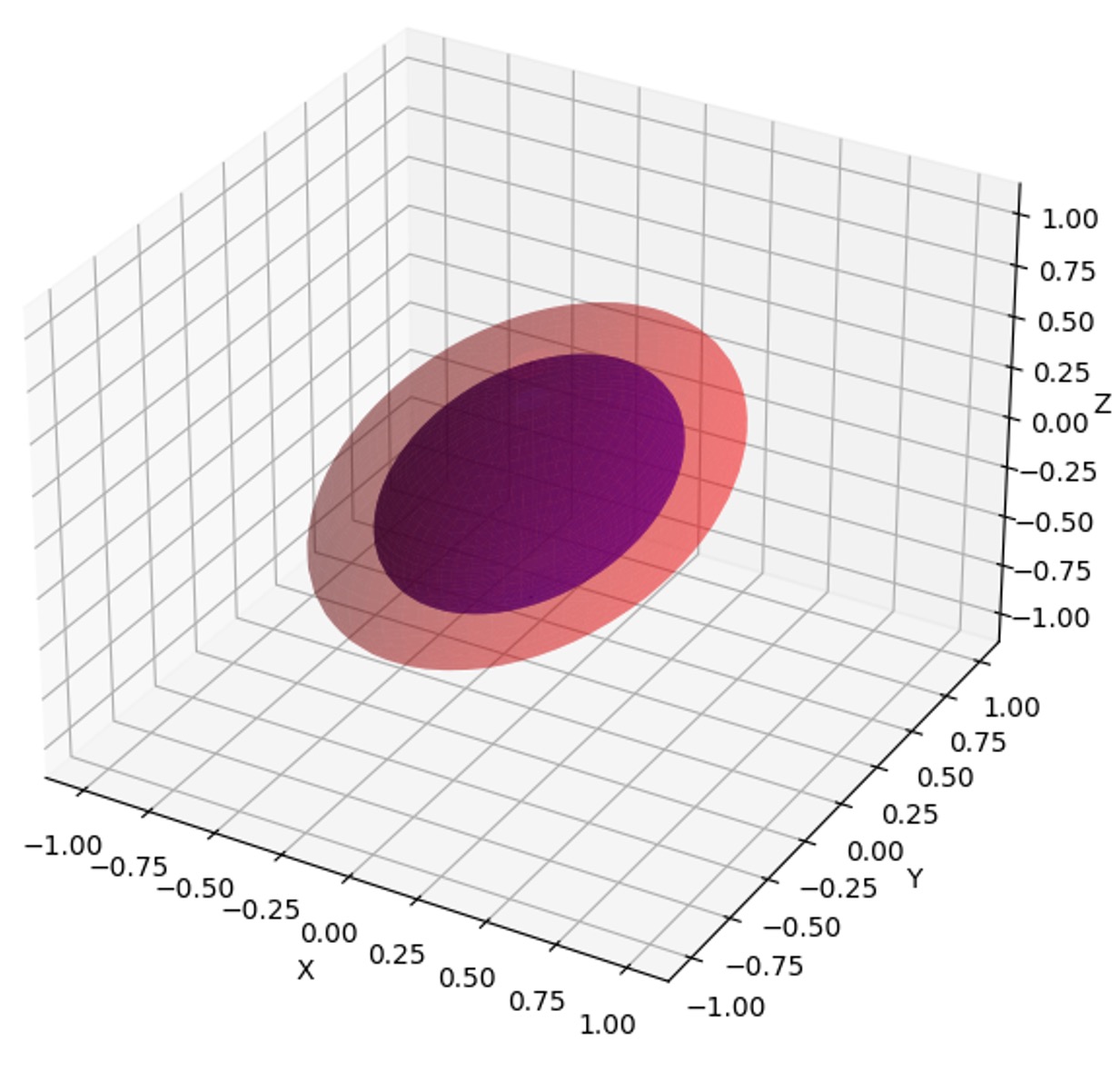
따라서 |V| = |V'| = (4π/3) × ((1/√3) × 1 × (1/√3) - (1/√6) × (1/√2) × (1/√12)) = π/3
3. 영역 W = {(x, y, z) ∈ ℝ3 : x2 + y2 ≤ 1, |z| ≤ 1}에서 두 벡터장 F와 G가 다음과 같이 주어져 있다.
F(x, y, z) = (sin xy, sin yz, 0), G(x, y, z) = (exp(x2 + y2 + z2), cos xz, 0)
다음 적분값을 구하여라. (단, curl(F) = ∇ × F이다.)
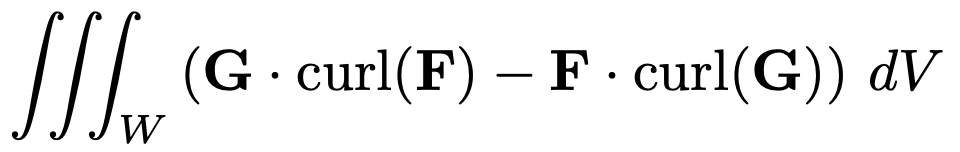
Solution.
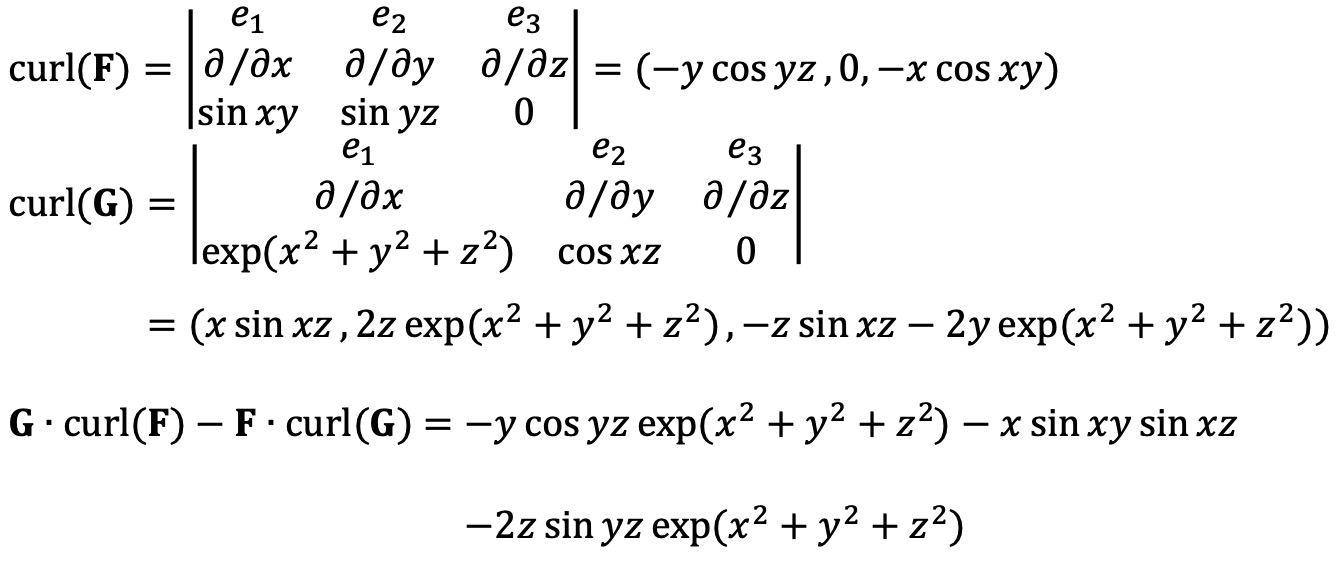
∫∫∫ -y cos yz exp(x2 + y2 + z2) dV = 0이다. 왜냐하면, (x, y, z)와 (x, -y, z)가 절댓값은 같고 부호가 달라 서로 상쇄되기 때문이다.
∫∫∫ -x sin xy sin xz dV = 0이다. 왜냐하면, (x, y, z)와 (-x, y, z)가 절댓값은 같고 부호가 달라 서로 상쇄되기 때문이다.
∫∫∫ -2z sin yz exp(x2 + y2 + z2) dV = 0이다. 왜냐하면, (x, y, z)와 (x, -y, z)가 절댓값은 같고 부호가 달라 서로 상쇄되기 때문이다.
그러므로 주어진 적분값은 0이다.
4. 크기가 n × n인 유니타리(unitary) 행렬 A와 B에 대하여, | det(A + 2B) | ≤ 3n임을 보여라.
Solution.
⑴ 유니타리 행렬의 정의 : 복소수 행렬 중에서 다음과 같은 조건을 만족하는 행렬
A · A* = A* · A = I
① A* : A의 에르미트 전치(Hermitian transpose). 즉, 행렬 A의 복소켤레를 취하고 전치(transpose)한 행렬
② I : n × n 단위행렬(identity matrix)
③ 유니타리 행렬은 실수 행렬에서 직교 행렬의 복소수 버전
⑵ 유니타리 행렬의 특성
① 모든 고유값의 절댓값이 1
② 열벡터가 정규직교(orthonormal)
③ 행벡터가 정규직교(orthonormal)
⑶ 문제 풀이
|| A + 2B ||2 ≤ || A ||2 + || 2B ||2 = || A ||2 + 2 || B ||2 = 1 + 2 = 3 (∵ || A ||2 = 1, || B ||2 = 1)
∴ | det(A + 2B) | ≤ ( || A + 2B ||2 )n = 3n
5. 수열 {an}n≥1은 다음과 같이 정의된다. (단, log는 자연로그이다.)
a1 = 1, an+1 = log ((ean - 1) / an)
수열 {bn}n≥1은 bn = ∏i = 1 to n ai으로 정의할 때, 급수 ∑n=1 to ∞ bn의 값을 구하여라.
Solution.
0 < x < 1에서 1 ≤ xex - ex + 1이 성립한다.
따라서, 0 < x < 1에서 [log ((ex - 1) / x)]' = [xex - ex + 1] / x(ex - 1) > 0이므로 log ((ex - 1) / x) < log (e-1) < 1이므로 an은 감소수열이다.
(ex - 1) / x = x0 / 1! + x/2! + x2 / 3! + ···이므로, x ≪ 1인 경우 log ((ex - 1) / x) ≒ x / 2가 성립한다.
그러므로, n이 충분히 크면, an+1 ≒ an / 2 < 1 /2와 같아서, bn+1 / bn = an+1 < 1/2이다.
따라서, 주어진 급수의 수렴성 및 limn → ∞ an = limn → ∞ bn = 0은 자명하다.
주어진 점화식 조건에 의해 anean+1 = ean - 1이 성립하므로, 최종적으로 다음이 성립한다.
e - 1 = ea1 - 1 = a1ea2 = a1(1 + a2e3) = a1(1 + a2(1 + a3(1 + ···)) = a1 + a1a2 + a1a2a3 + ··· = ∑n=1 to ∞ bn
6. 적분 가능한 함수 f : [0, ∞) → [0, ∞)가 다음을 만족한다.
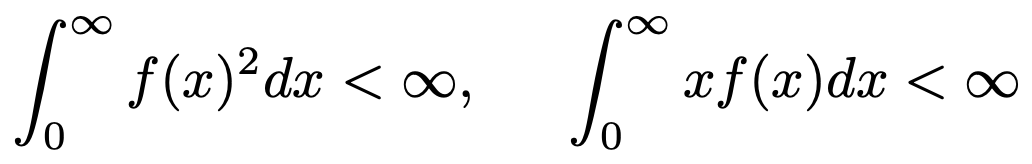
다음 부등식을 증명하여라.
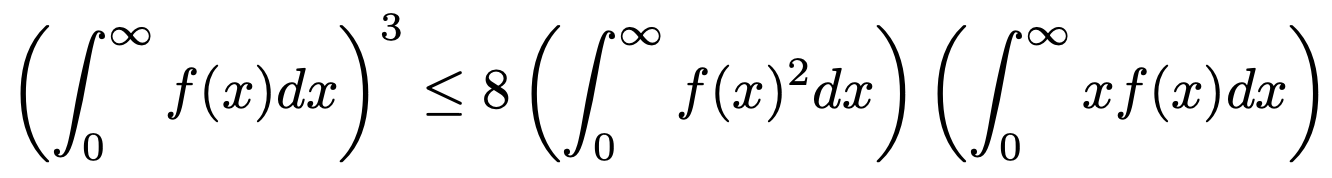
Solution.
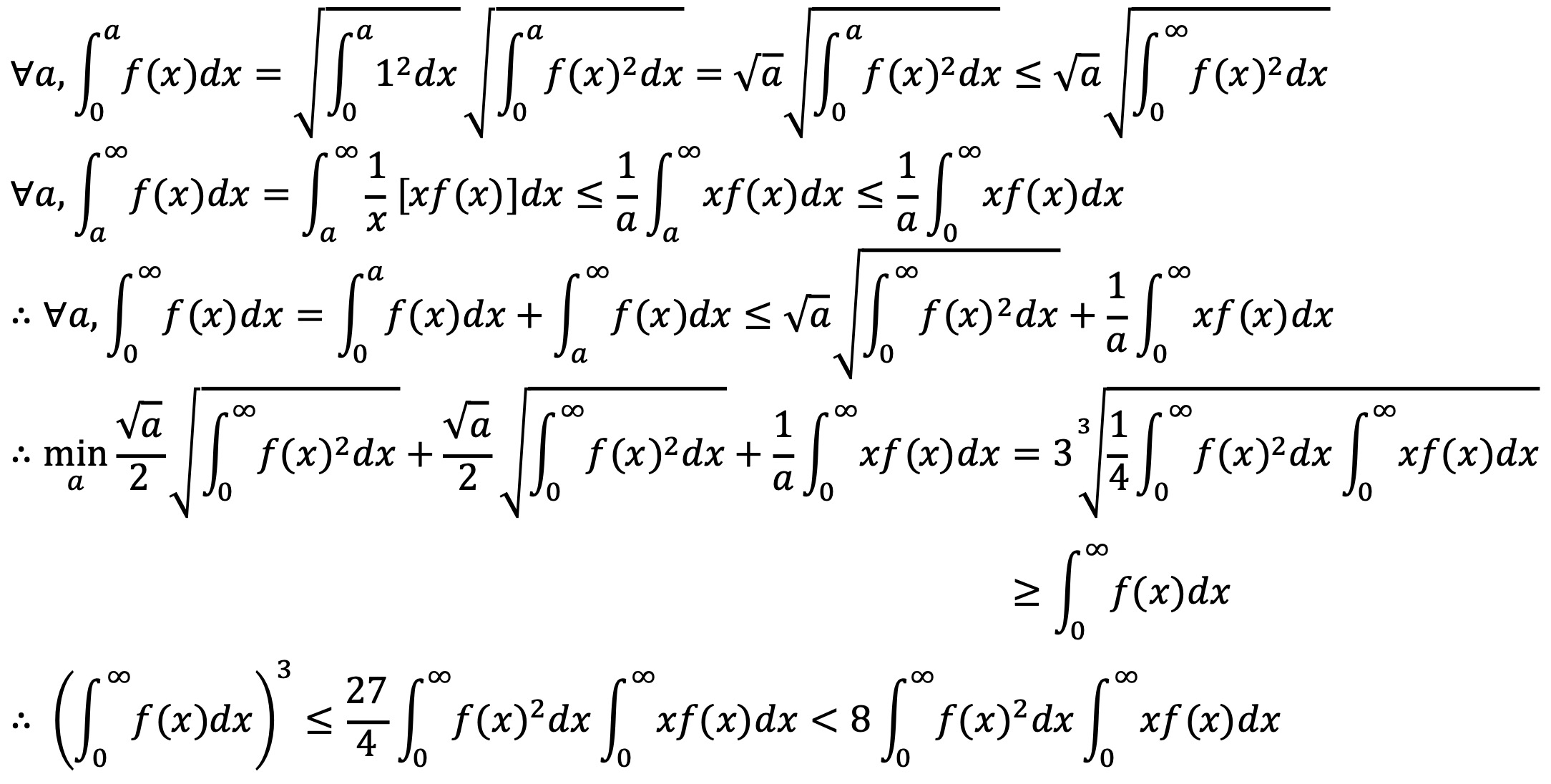
7. 실수 a와 정수 n (n ≥ 2)에 대하여 Sn(a)를 다음과 같이 정의하자.
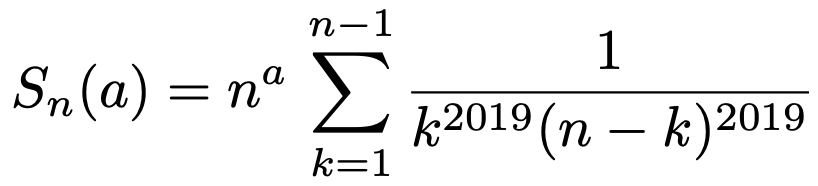
수열 {Sn(a)}n≥2가 양의 실수로 수렴하는 a의 값을 모두 구하여라.
Solution.
a = 2019인 경우 다음과 같다.
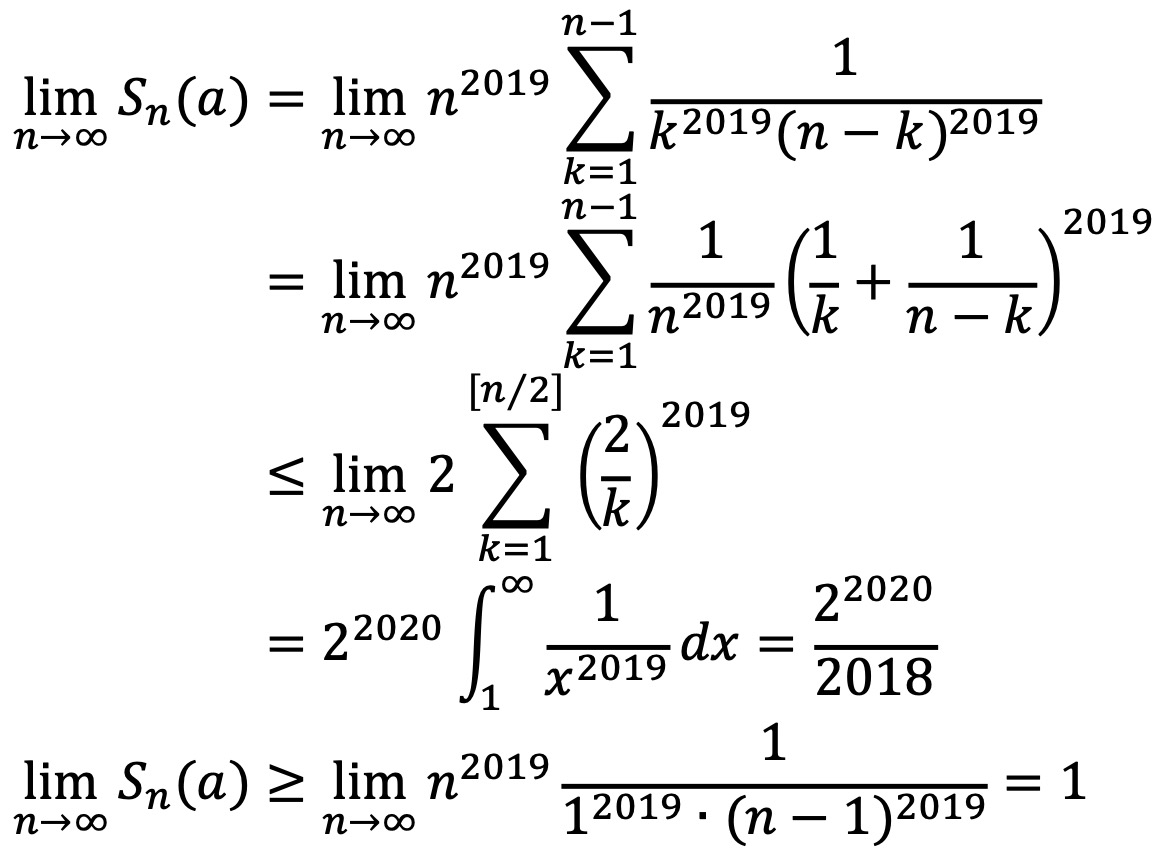
그러므로 완비성 공리에 의해 Sn(a)는 n → ∞에 대하여 수렴값이 존재하고, 그 값은 양의 실수이다.
한편, a > 2019이면 Sn(a)는 무한대로 발산하고, a < 2019이면 Sn(a)는 0으로 수렴한다.
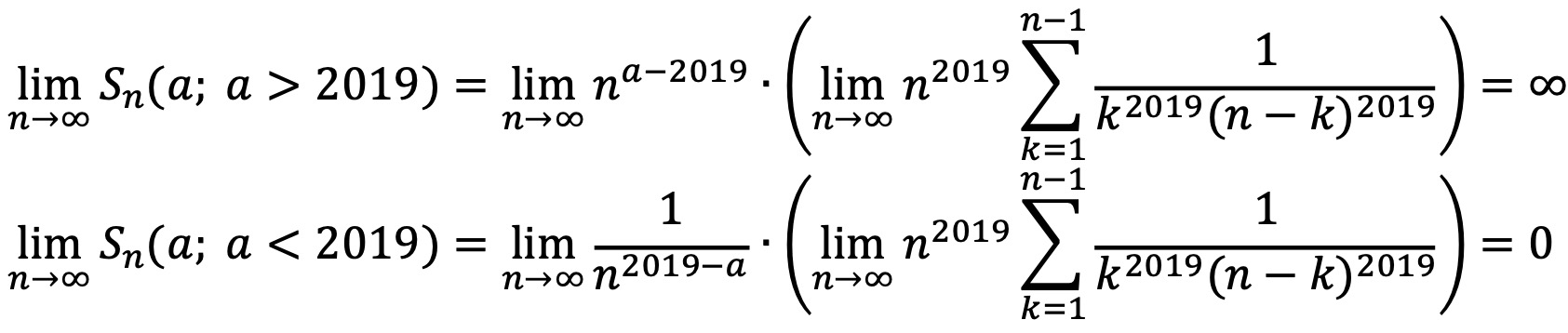
따라서 주어진 수열이 양의 실수로 수렴하는 a는 2019밖에 없다.
8. 크기가 n × n인 복소행렬들로 이루어진 복소벡터공간을 Mn(ℂ)라고 하자. 선형사상 T : Mn(ℂ) → Mn(ℂ)는 임의의 A ∈ Mn(ℂ)에 대하여 det(A) = det(T(A))를 만족한다.
⑴ 행렬 T(A)가 영행렬이면, A가 영행렬임을 보여라.
⑵ 임의의 A ∈ Mn(ℂ)에 대하여 rank(A) = rank(T(A))임을 보여라.
Solution.
⑵를 증명하면 ⑴은 자동으로 증명된다. (∵ 영행렬은 rank가 0인 유일한 행렬)
⑵에 대한 증명은 공식 풀이를 참고하였다.
우선, rank(A) = s, rank (ϕ(A)) = t라 두면, 다음을 만족하는 가역인 행렬 Ui, Vj를 잡을 수 있다.
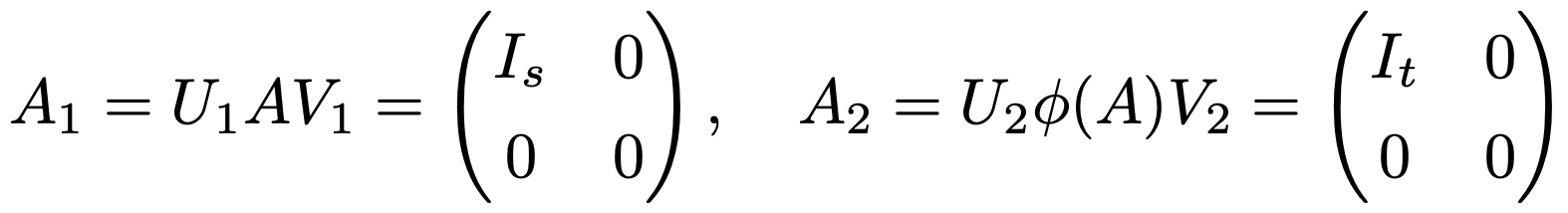
또한 B = U1-1V1-1이라 두자.
그러면 임의의 복소수 x ∈ ℂ에 대하여 다음을 만족한다.
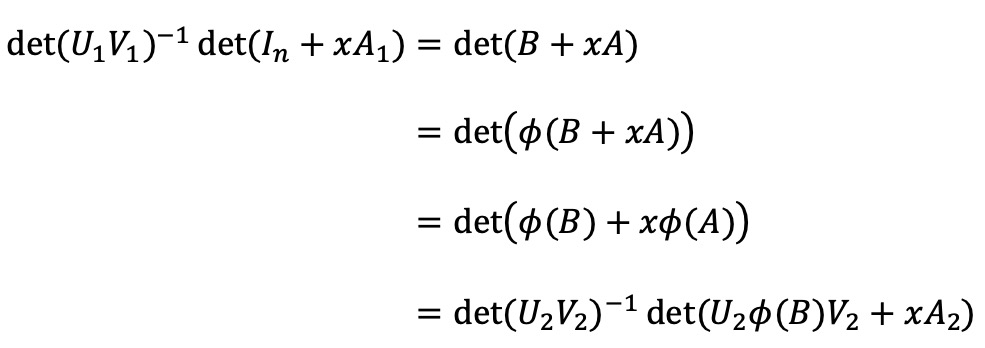
위 식은 모든 복소수 x에 대해 성립하므로, |x| → ∞으로 보내는 경우에도 동일하다.
따라서, x에 대한 차수가 동일해야 한다는 점에서 s = t 를 쉽게 보일 수 있다.
입력: 2024.12.27 13:36
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 1 분야 (4) | 2025.01.06 |
|---|---|
| 【대수경】 제 38회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.12.29 |
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.12.08 |
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.12.07 |
| 【대수경】 제 39회 전국 대학생 수학 경시대회 제 2 분야 (4) | 2024.12.06 |




최근댓글