제 39회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 39회 전국 대학생 수학경시대회
제 2 분야
2020년 11월 14일 (10:00 - 11:30)
1. 다음 극한값을 구하여라.
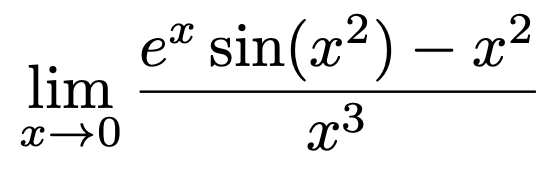
Solution.
ex = 1 + x + x2 / 2! + x3 / 3! + ···
sin(x) = x - x3 / 3! + x5 / 5! - ···
sin(x2) = x2 - x6 / 3! + x10 / 5! - ···
∴ ex·sin(x2) = x2 + x3 + x4 / 2! + x5 / 3! + ···
∴ ex·sin(x2) - x2 = x3 + x4 / 2! + x5 / 3! + ···
∴ (준식) = 1
2. 양의 정수 n ≥ 2에 대하여, n × n 대칭행렬 M = (mij)을 다음과 같이 정의하자.

이때, 다음 식의 값을 n에 대한 다항식으로 표현하여라.
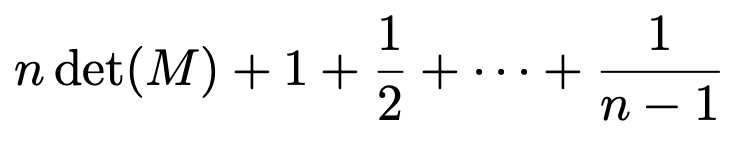
Solution.
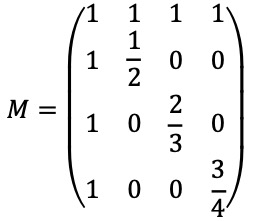
n × n 행렬 M이 위와 같을 때 여인수 전개(cofactor expansion)에 의해 det(M) = an을 다음과 같이 나타낼 수 있다.
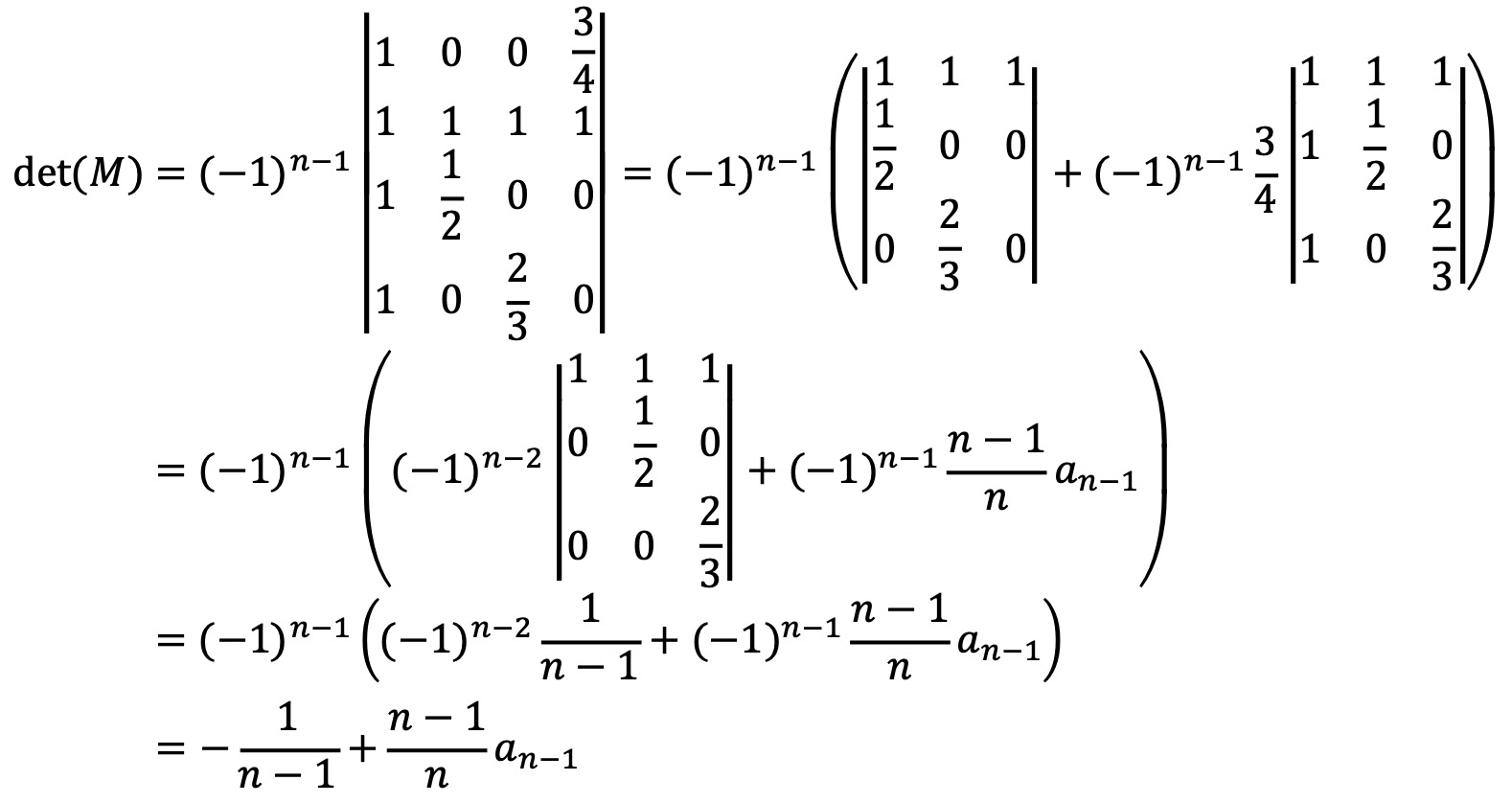
n = 2일 때 det(M) = -1/2이므로, (준식)은 최종적으로 다음과 같이 나타낼 수 있다.
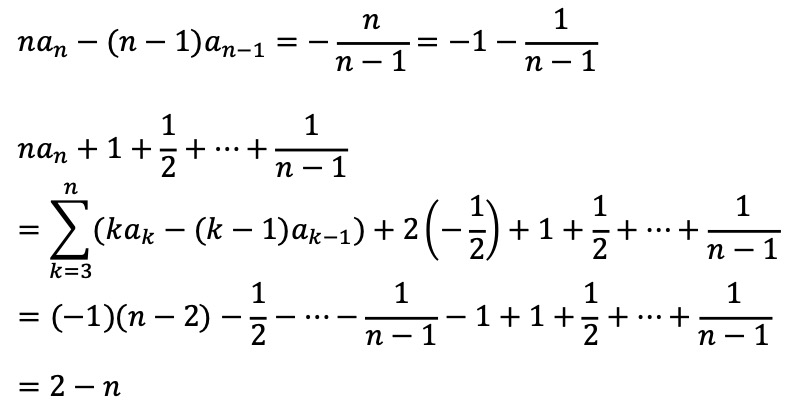
3. 이변수함수 f(x, y)는 다음과 같이 정의된다.
f(x, y) = 3 + 2 cosx + 2 cosy + 2 cos(x - y)
⑴ 모든 실수 x, y에 대하여, f(x, y) ≥ 0임을 보여라.
⑵ 영역 {(x, y) ∈ ℝ2 : -π ≤ x, y ≤ π}에서 f(x, y) = 0이 되는 (x, y)를 모두 구하여라.
Solution.
⑴
f는 모든 점에서 미분 가능하므로 f의 최솟값은 f의 극값에서 결정된다.
∇f = (-2 sinx - 2 sin(x - y), -2 sin y - 2 sin(y - x))이다.
한편, sin x + sin (x - y) = 2 sin(x - y/2) cos(y / 2) = 0이 성립하므로 x - y / 2 = mπ, m ∈ ℤ 혹은 y / 2 = (n + 1 / 2)π, n ∈ ℤ이다.
또한, sin y + sin (y - x) = 2 sin(y - x/2) cos(x / 2) = 0이 성립하므로 y - x / 2 = m'π, m' ∈ ℤ 혹은 x / 2 = (n' + 1 / 2)π, n' ∈ ℤ이다.
경우 1. x - y / 2 = mπ, m ∈ ℤ 그리고 y - x / 2 = m'π, m' ∈ ℤ
(x + y) / 2 = (m + m')π이므로 x = 2(2m + m')π / 3, y = 2(m + 2m')π / 3이다.
f의 최솟값 후보는
① f(0, 0) = 9,
② f(0, 2π/3) = 3,
③ f(0, 4π/3) = 3,
④ f(2π/3, 0) = 3,
⑤ f(2π/3, 2π/3) = 3,
⑥ f(2π/3, 4π/3) = 0,
⑦ f(4π/3, 0) = 3,
⑧ f(4π/3, 2π/3) = 0,
⑨ f(4π/3, 4π/3) = 3
이다.
경우 2. x - y / 2 = mπ, m ∈ ℤ 그리고 x / 2 = (n' + 1 / 2)π, n' ∈ ℤ
x = (2n' + 1)π, n' ∈ ℤ이고 y = 2x - 2mπ = (4n' + 2 - 2m)π이다.
사실상 x = π, y = 0으로 보아도 무방하므로 경우 2에서 기술되는 f의 최솟값 후보는 f(π, 0) = 1이다.
경우 3. y / 2 = (n + 1 / 2)π, n ∈ ℤ 그리고 y - x / 2 = m'π, m' ∈ ℤ
cos(y - x) = cos (x - y)이므로 대칭성에 의해 경우 2와 동일하게 f의 최솟값 후보는 f(0, π) = 1이다.
경우 4. y / 2 = (n + 1 / 2)π, n ∈ ℤ 그리고 x / 2 = (n' + 1 / 2)π, n' ∈ ℤ
x = (2n' + 1)π, y = (2n + 1)π이다.
사실상 x = y = π이므로 경우 4에서 기술되는 f의 최솟값 후보는 f(π, π) = 1이다.
그러므로 f의 최솟값은 0이다.
⑵
f(x, y) = 0은 f의 최솟값이므로 (x, y)는 ⑴에서 기술되는 극점이어야 한다.
그러므로 {(2π / 3, -2π / 3), (-2π / 3, 2π / 3)}이 답이 된다.
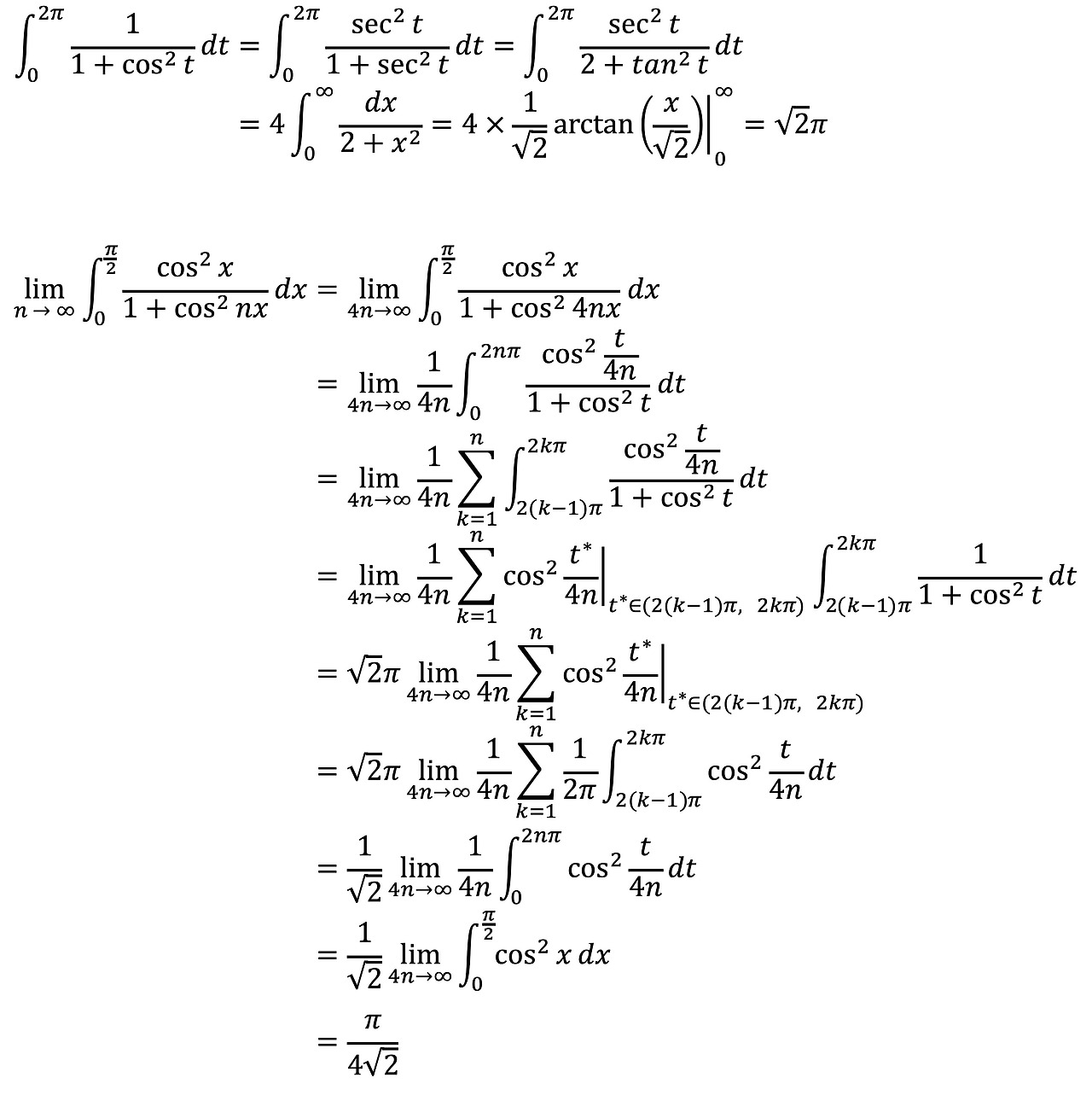
4. 다음 극한값을 구하여라.
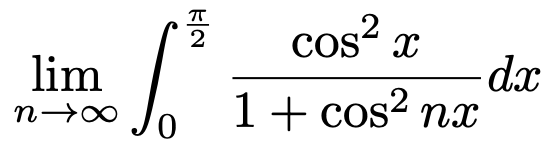
Solution.
5. 다음 세 행렬이 공통의 고유벡터를 갖기 위한 a, b의 필요충분조건을 구하여라.
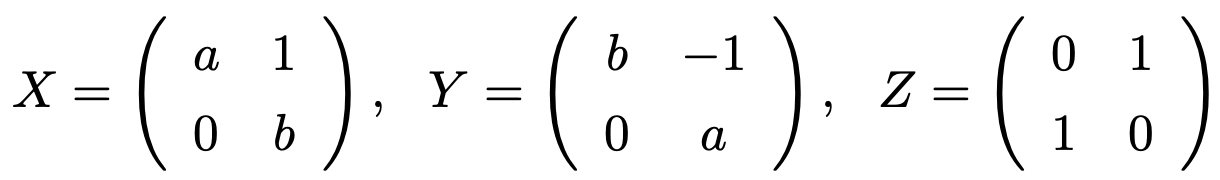
Solution.
증명 1. 세 행렬이 공통의 고유벡터를 가지면 b = a ± 1을 만족한다.
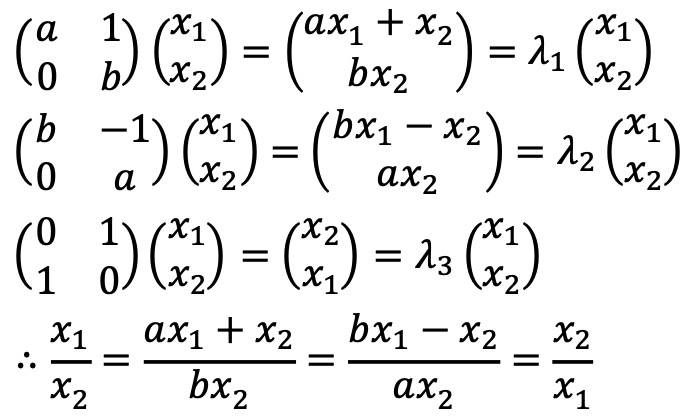
0 = x12 - x22 = (x1 - x2)(x1 + x2)이므로, x1 / x2 = 1 or -1이 성립한다.
x1 = x2인 경우, 1 = (a + 1) / b = (b - 1) / a로부터 b = a + 1을 얻을 수 있다.
x1 = -x2인 경우, -1 = (-a + 1) / b = (-b - 1) / a로부터 b = a - 1을 얻을 수 있다.
증명 2. b = a ± 1을 만족하면 세 행렬은 공통의 고유벡터를 가진다.
b = a + 1인 경우 다음이 성립한다.
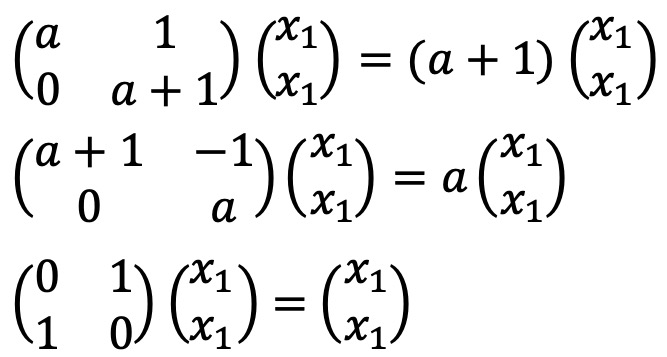
b = a - 1인 경우 다음이 성립한다.
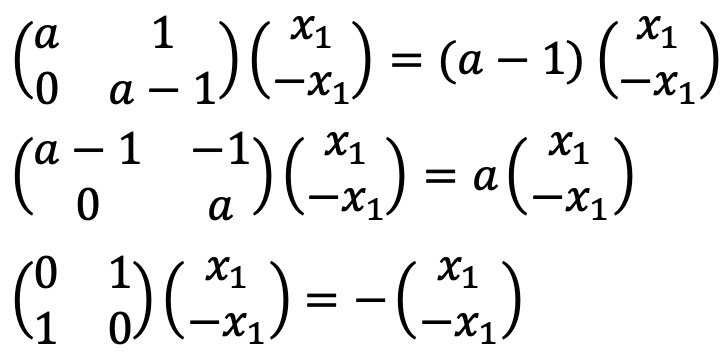
6. 세 벡터 wi = (ai1, ai2, ai3) ∈ ℝ3 (i = 1, 2, 3)에 대하여, 행렬 (aij)1≤i,j≤3의 행렬식을 |w1, w2, w3|이라고 하자. 임의의 여섯 벡터 u1, u2, u3, v1, v2, v3 ∈ ℝ3에 대하여, 다음 등식이 성립함을 보여라.
|u1, u2, u3| |v1, v2, v3| = |v1, u2, u3| |u1, v2, v3| + |u1, v1, u3| |u2, v2, v3| + |u1, u2, v1| |u3, v2, v3|
Solution.
정식 풀이는 여인수 전개를 활용하지만, 여기에서는 좀 다른 풀이를 소개하고자 한다.
치환을 활용하여 주어진 식을 다음과 같이 나타낼 수 있다.
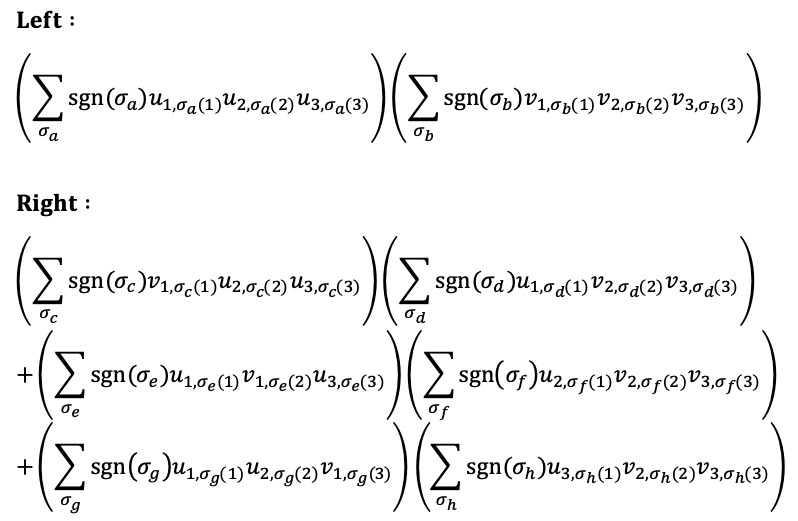
경우 1. σa(1) = σb(1)
조건을 만족하는 임의의 (σa, σb)에 대하여,
sgn(σa)u1,σa(1)u2,σa(2)u3,σa(3)·sgn(σb)v1,σb(1)v2,σb(2)v3,σb(3) [좌변]
= sgn(σc)v1,σc(1)u2,σc(2)u3,σc(3)·sgn(σd)u1,σd(1)v2,σd(2)v3,σd(3) [우변의 첫 번째 항]
가 성립하도록 σc = σa, σd = σb와 같이 설정할 수 있다.
또한, 임의의 (σe, σf)에 대하여,
u1,σe(1)v1,σe(2)u3,σe(3)·u2,σf(1)v2,σf(2)v3,σf(3) [우변의 두 번째 항]
= u1,σg(1)u2,σg(2)v1σg(3)·u3,σh(1)v2,σh(2)v3,σh(3) [우변의 세 번째 항]
이면서 sgn(σe)·sgn(σf) = -sgn(σg)sgn(σh)인 (σg, σh)가 일대일 대응으로 존재한다.
즉, σe = σg, σf = σh라고 둔 뒤 σe(2)와 σe(3)이 서로 뒤바뀐 경우이고, [두 번째 항], [세 번째 항]의 sgn(·)·sgn(·)의 부호가 달라진다.
이때, σa(1) = σb(1) = σe(1) = σf(1) = σg(1) = σh(1)로 둔다는 점에서 σa(1) = σb(1) 조건이 필요하다.
구체적으로는,
σe(1) = σg(1) = σa(1) = σb(1) : u1,σe(1)과 u1,σg(1)이 매칭됨
σe(2) = σg(3) : v1,σe(2)와 v1,σg(3)가 매칭됨
σe(3) = σg(2) = σh(1) : u3,σe(3)과 u3,σh(1)이 매칭됨
σf(1) = σg(2) = σh(1) : u2,σf(1)과 u2,σg(2)가 매칭됨
σf(2) = σh(2) : v2,σf(2)와 v2,σh(2)가 매칭됨
σf(3) = σh(3) : v3,σf(3)과 v3,σh(3)이 매칭됨
σg(2) = σh(1)인 이유 : {σg(1), σg(2), σg(3)} = {σh(1), σh(2), σh(3)} = {1, 2, 3}이기 때문이다.
요약하면, 경우 1에서 [우변의 두 번째 항]은 [우변의 세 번째 항]과 서로 상쇄되어 그 합은 0이 된다.
경우 2. σa(2) = σb(1)
조건을 만족하는 임의의 (σa, σb)에 대하여,
sgn(σa)u1,σa(1)u2,σa(2)u3,σa(3)·sgn(σb)v1,σb(1)v2,σb(2)v3,σb(3) [좌변]
= sgn(σe)u1,σe(1)v1,σe(2)u3,σe(3)·sgn(σf)u2,σf(1)v2,σf(2)v3,σf(3) [우변의 두 번째 항]
가 성립하도록 σe = σa, σf = σb와 같이 설정할 수 있다.
경우 1과 비슷하게, [우변의 첫 번째 항]은 [우변의 세 번째 항]과 서로 상쇄되어 그 합은 0이 된다. (∵ 대칭성의 원리)
경우 3. σa(3) = σb(1)
조건을 만족하는 임의의 (σa, σb)에 대하여,
sgn(σa)u1,σa(1)u2,σa(2)u3,σa(3)·sgn(σb)v1,σb(1)v2,σb(2)v3,σb(3) [좌변]
= sgn(σg)u1,σg(1)u2,σg(2)v1,σg(3)·sgn(σh)u3,σh(1)v2,σh(2)v3,σh(3) [우변의 세 번째 항]
가 성립하도록 σg = σa, σh = σb와 같이 설정할 수 있다.
경우 1과 비슷하게, [우변의 첫 번째 항]은 [우변의 두 번째 항]과 서로 상쇄되어 그 합은 0이 된다. (∵ 대칭성의 원리)
경우 1, 경우 2, 경우 3은 서로 교집합이 없고 그 합집합이 전체 집합을 이루는 분할 관계이므로, 주어진 명제가 성립함을 증명하였다.
7. 다음 극한값을 구하여라.
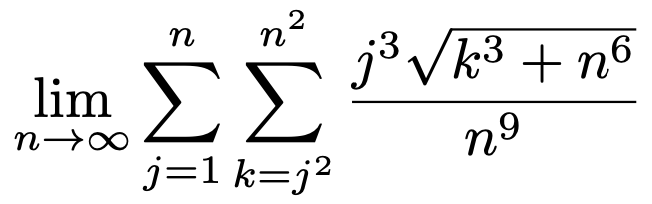
Solution.
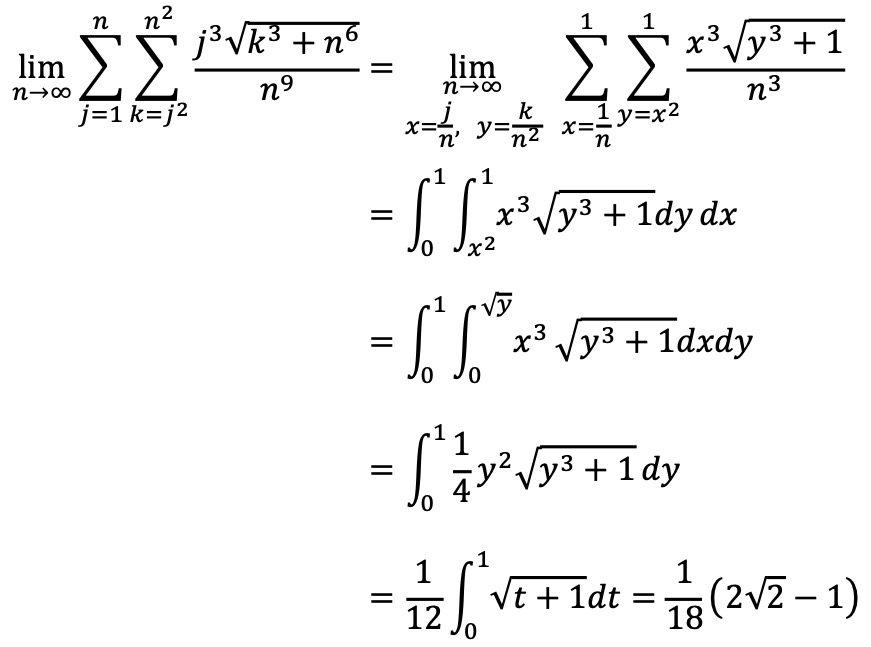
8. 구간 [0, ∞)에서 정의된 미분 가능한 실함수 x(t), y(t)가 (x(0), y(0)) = (2020, 2020)이고, 모든 양수 t에 대하여 다음 방정식을 만족한다고 하자.
x'(t) = -2x(t)y(t) + 3x(t) + 1
y'(t) = x(t)2 - x(t) - y(t) + 2
이때, 다음 극한값이 존재함을 보이고 그 값을 구하여라.
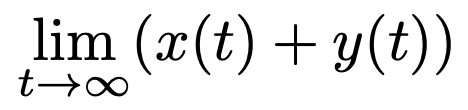
Solution.
직관적으로 (x(t), y(t))가 존재함을 보일 수 있다.
맨 처음에 x(0)와 y(0) 값이 충분히 크므로 x'(t)이 큰 음수 값을 가지고 y'(t)는 큰 양수 값을 가진다.
그러다 보면 x(t)가 비교적 작아지고 y(t)가 비교적 커지는 순간이 와 y'(t)도 음수가 된다.
따라서 (x(t), y(t))는 (+∞, +∞)으로 발산하지 않는다.
비숫하게 (x(t), y(t))가 무한대로 발산하지 않음을 보일 수 있다.
x'(t) = y'(t) = 0으로부터 극점은 (-1.34, 1.13), (-0.15, -1.83), (2.49, 1.70)을 얻는다.
극점 주변에 대한 선형 근사(linearization) 및 Jacobian 행렬은 다음과 같다.
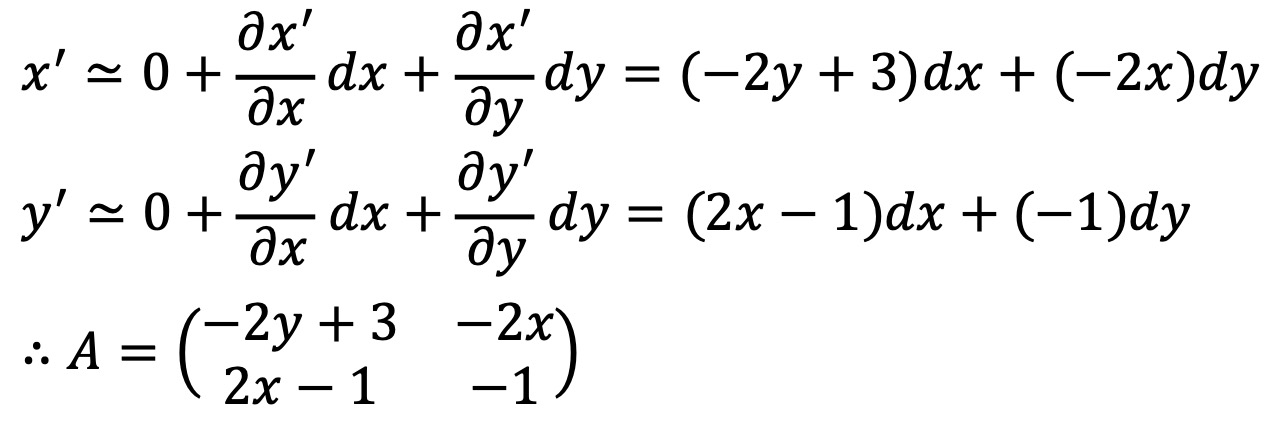
(-1.34, 1.13)에 대한 Jacobian 행렬은 -0.13 ± i 3.02의 고유치를 가지므로 주위에 spiral 패턴이 나타난다.
(-0.15, -1.83)에 대한 Jacobian 행렬은 6.61, -0.95이므로 안장점이다.
(2.49, 1.70)에 대한 Jacobian 행렬은 -0.7 ± i 4.44의 고유치를 가지므로 주위에 spiral 패턴이 나타난다.
다만, 선형 근사는 극점 바로 근처에서만 성립할 뿐 조금 벗어나면 위 패턴이 나타나지 않을 수 있음을 주의하자.
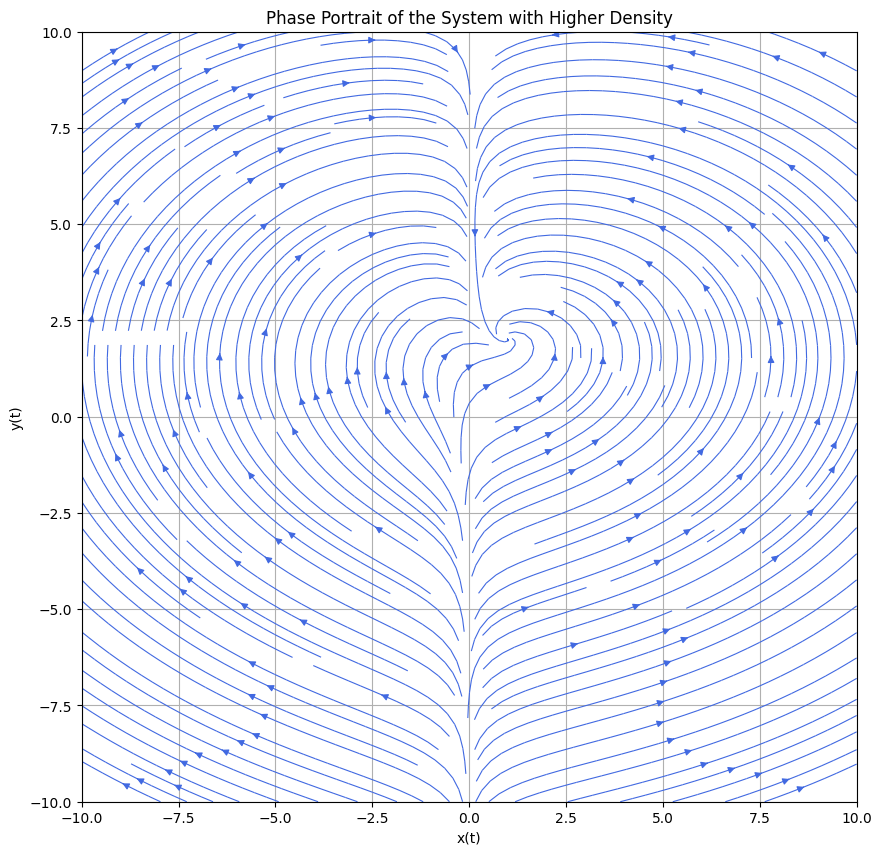
이때, 3개의 극점 중에서 (2020, 2020)과 가까운 (2.49, 1.70)이 최종 수렴 지점이 되며, 그러므로 그 값은 4.19가 된다.
실제로 다음은 주어진 시스템에 대한 phase portrait (혹은 flow diagram)이다.
import numpy as np
import matplotlib.pyplot as plt
# Define the system of differential equations
def system(X, Y):
x_prime = -2 * X * Y + 3 * X + 1
y_prime = X**2 - X - Y + 2
return x_prime, y_prime
# Set up the grid for the phase portrait with higher density
x_values = np.linspace(-10, 10, 600) # Higher density
y_values = np.linspace(-10, 10, 600)
X, Y = np.meshgrid(x_values, y_values)
# Calculate the flow of the system at each point in the grid
U, V = system(X, Y)
# Normalize the vectors for better visualization
magnitude = np.sqrt(U**2 + V**2)
U /= magnitude
V /= magnitude
# Plotting the phase portrait with higher density
plt.figure(figsize=(10, 10))
plt.streamplot(X, Y, U, V, color='royalblue', linewidth=0.8, density=2) # Increased density
plt.title("Phase Portrait of the System with Higher Density")
plt.xlabel("x(t)")
plt.ylabel("y(t)")
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.grid(True)
plt.show()
육안으로도 (x(t), y(t))가 (2020, 2020)에서 시작하여 (2.49, 1.70)으로 수렴할 것임을 알 수 있다.
입력: 2024.11.21 08:46
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.12.08 |
|---|---|
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.12.07 |
| 【대수경】 제 39회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2024.10.04 |
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.04.06 |
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 1 분야 (1) | 2024.04.06 |




최근댓글