제 40회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 40회 전국 대학생 수학경시대회
제 1 분야
2021년 11월 13일 (10:00 - 11:30)
1. 함수 f(x, y, z) = exp(x2y) sin z에 대하여 ∇f(√2, 1/2, π/4)를 구하여라. 단, ∇f는 f의 그래디언트(gradient)이다.
Solution.

2. 크기가 n × n인 실행렬들로 이루어진 실벡터공간을 Mn(ℝ)이라 하자. 행렬 A ∈ Mn(ℝ)에 대하여 선형사상 ΦA : Mn(ℝ) → Mn (ℝ)을 ΦA(X) = AX - XA로 정의할 때, det (ΦA)와 tr (ΦA)를 구하여라.
Solution.
ΦA는 n2 차원 벡터를 n2 차원 벡터로 옮기는 n2 × n2 선형 사상이라는 사실을 유의
ΦA (I) = A - A = O이므로 ker (ΦA) ≠ ∅가 되어 det(ΦA) = 0임을 쉽게 알 수 있다. (∵ rank-nullity theorem)
이제 tr(ΦA)를 구해보자. ΦA(X)는 다음과 같이 나타낼 수 있다.

ΦA(X) = (a1 · x1 + a2 · x2 + ··· + an · xn) - (x1* · a1* + x2* · a2* + ··· + xn* · an*)
그러므로 tr(ΦA)는 다음과 같다.
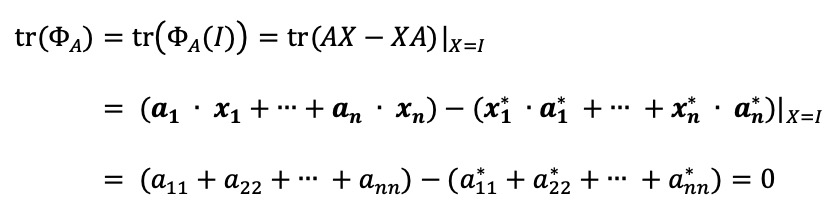
3. 다음 적분값을 구하여라.
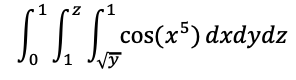
Solution.
테일러 급수를 이용한다.
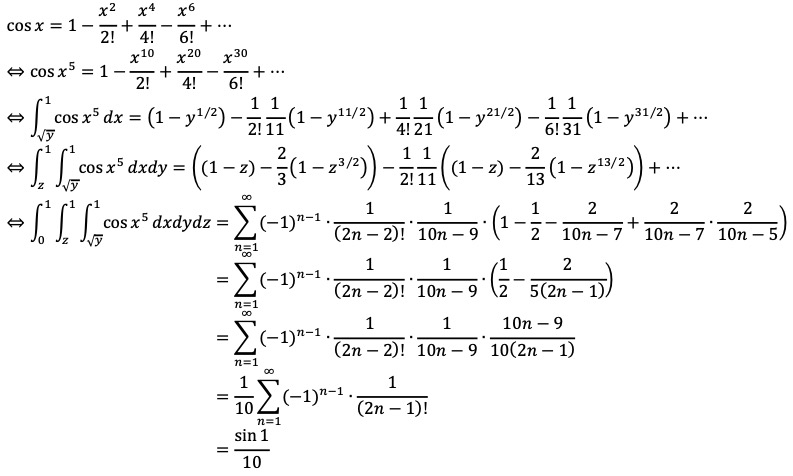
4. 크기가 n × n인 실대칭행렬 A = (aij)는 서로 다른 임의의 i, j에 대하여 aij ≤ 0을 만족하고, A의 모든 고윳값은 음이 아닌 실수이다. (단, n ≥ 2)
⒜ 행렬 A의 영공간을 N(A)라고 하자. 이때 다음을 보여라.
N(A) = { v ∈ ℝn : v · Av = 0 }
⒝ 집합 {1, 2, ..., n}의 임의의 진분할 I, J에 대하여 aij ≠ 0인 i ∈ I와 j ∈ J가 항상 존재한다고 가정하자. 이때 다음을 보여라.
dim N(A) ≤ 1
(단, 공집합이 아닌 두 집합 I, J가 I ∪ J = {1, 2, ···, n}이고 I ∩ J = ∅일 때, I, J를 {1, 2, ···, n}의 진분할이라고 하자.
Solution.
⒜ 공식 풀이를 참고하였다.
가정에 의하여 PtAP = D (단, D는 직교행렬)이 되는 적당한 직교행렬 P가 존재한다.
이때 대각행렬 D의 대각원소를 d1, ···, dn이라고 하면 가정에 의하여, 모든 i = 1, ···, n에 대하여 di ≥ 0이 성립한다.
영공간의 정의
N(A) = { v ∈ ℝn : Av = 0 }
으로부터
N(A) ⊂ { v ∈ ℝn : v · Av = 0 }
은 자명하다. (단, vt는 v의 전치행렬)
역으로, v가 vtAv = 0을 만족한다고 하자.
이때 w = Ptv라고 하면,
0 = vtAv = vtPPtAPPtv = wtDw
가 된다. 그리고 di ≥ 0이라는 사실로부터 Dw = 0을 확인할 수 있다.
따라서
0 = vtAv = vtPPtAPPtv = wtDw
이므로 Av = 0이 성립한다.
⒝ 공식 풀이를 참고하였다.
영공간 N(A)의 차원이 0보다 크다고 가정하자. 즉, dim N(A) > 0 - 가정 1
0이 아닌 벡터 x ∈ N(A)에 대하여 x의 성분의 절대값으로 이루어진 벡터를 z라고 하자.
서로 다른 임의의 i, j에 대하여 aij ≤ 0을 만족한다는 주어진 가정을 염두에 두고 ztAz, xtAx 식을 전개하면 다음을 얻을 수 있다.
0 ≤ ztAz ≤ xtAx = 0
따라서 ⒜에 의해, 임의의 x ∈ N(A)의 성분의 절대값으로 이루어진 벡터 z는 z ∈ N(A)를 만족한다. - 명제 1
한편, z = (z1, z2, ···, zn)에서 zi = 0인 모든 i의 집합을 I라고 하고, J = {1, 2, ···, n} - I라 하자. - 가정 2
이때, z ∈ N(A)로부터 다음이 성립함을 유의하자.
Az = 0, 또는
∑j a1j zj = 0
⋮
∑j anj zj = 0
그런데, 가정 2 하에 ∑j aij zj = 0이 성립할 수 있을까? i ∈ I라 두면,
0 = ∑j aij zj = ∑j*∈J aij* zj*, zj* > 0
⇔ aij* = 0 ∀ j* ∈ J
이는 aij* ≠ 0 ∃ j* ∈ J라는 주어진 조건과 모순이다.
따라서 가정 2은 틀렸고, 그러므로 I 또는 J가 존재하지 않는다.
그리고 aij* ≠ 0 ∃ j* ∈ J라는 조건을 조금만 검토하면 I가 존재하지 않는다는 것을 알 수 있다. - 명제 2
z의 모든 성분이 양수이므로 x의 모든 성분이 0이 아님을 알 수 있다. - 명제 3
dim N(A) > 1이라고 가정하자. - 가정 3
이때 x, y ∈ N(A)인 일차독립인 x, y를 찾을 수 있다.
∀a, b ∈ ℝ, ax + by ∈ N(A)인데 ax + by의 임의의 한 성분이 0이 되도록 a, b를 적절하게 선택할 수 있다. - 명제 4
명제 4는 명제 3과 모순이므로, 가정 3은 틀렸다.
가정 1 및 가정 3의 역에 의해 dim N(A) ≤ 1이 성립한다.
5. 다음 적분값을 구하여라.
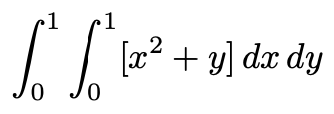
(단, [t]는 실수 t를 넘지 않는 가장 큰 정수이다.)
Solution.
주어진 적분 구간에서 [x2 + y]는 다음과 같은 분포를 갖는다.
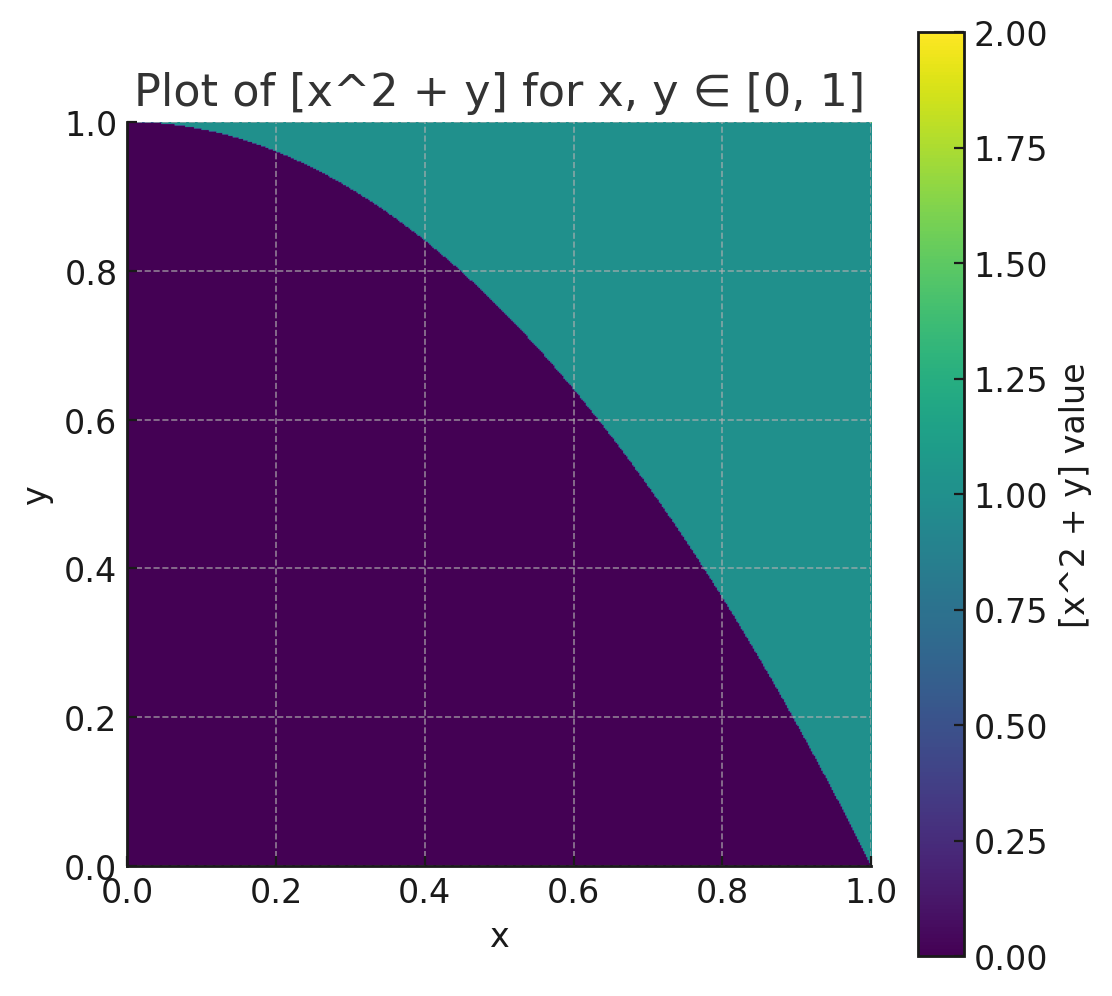
import numpy as np
import matplotlib.pyplot as plt
# Define the resolution of the grid
resolution = 500
# Create a grid of x and y values
x = np.linspace(0, 1, resolution)
y = np.linspace(0, 1, resolution)
# Create a meshgrid for x and y
X, Y = np.meshgrid(x, y)
# Calculate [x^2 + y] where [] denotes the floor function
Z = np.floor(X**2 + Y)
# Plotting
plt.figure(figsize=(6, 6))
plt.imshow(Z, origin='lower', extent=[0, 1, 0, 1], cmap='viridis')
plt.colorbar(label='[x^2 + y] value')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Plot of [x^2 + y] for x, y ∈ [0, 1]')
plt.show()
따라서, 주어진 적분식은
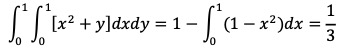
6. 크기가 n × n인 서로 다른 k개의 가역행렬들로 이루어진 집합 S = {A1, A2, ···, Ak}가 있다. (단, n, k ≥ 2) 임의의 Ai ∈ S에 대하여 S = {A1Ai, A2Ai, ···, AkAi}가 성립할 때,
(A1 + A2 + ··· + Ak) - At
가 가역행렬이 되는 At ∈ S가 존재함을 보여라.
Solution.
M을 다음과 같이 정의하자.
M = A1 + A2 + ··· + Ak
주어진 조건에 의해,
M × A1 = M
M × A2 = M
⋮
M × Ak = M
따라서, M × (A1 + ··· + Ak) = M2 = kM이 성립한다.
M2 - kM + (k/2)2 I = (k/2)2 I이 성립하므로, M = (k/2) I ± (k/2) I = O or kI가 성립한다.
경우 1. M = O
(A1 + ⋯ + Ak) - At = M - At = -At이므로 A1, ⋯, Ak가 가역이라는 사실로부터 쉽게 준 명제가 성립한다.
경우 2. M = kI
M × At = kAt = At (단, At = 가역행렬)로부터 k = 1이 성립한다.
이는 k ≥ 2라는 조건과 모순이다.
그러므로 준 명제가 성립한다.
7. 크기가 3 × 3인 직교행렬 A와 B가 유한집합
{(x, y, z) ∈ ℝ : x, y, z는 정수, x2 + y2 + z2 ≤ 2 }
에서 고윳값이 -1인 고유벡터를 두 개, 고윳값이 1인 고유벡터를 세 개 이상 가진다고 하자. 이때 (AB)2, (AB)3, (AB)4 중에 적어도 하나는 단위행렬 I3임을 보여라.
Solution.
주어진 유한집합을 R이라 하면, R = {(0, 0, 0), (±1, 0, 0), (0, ±1, 0), (0, 0, ±1), (±1, ±1, 0), (±1, 0, ±1), (0, ±1, ±1)}와 같다.
임의의 v ∈ R가 있으면, -v ∈ R도 성립한다.
A가 R에서 고윳값이 -1인 고유벡터를 두 개 가지고 있음은 어떤 ±v ∈ R이 있어 Av = -v, A(-v) = v가 성립한다는 의미이다.
또한, A가 R에서 고윳값이 1인 고유벡터를 세 개 이상 가지고 있음은 ±v2, ±v3 ∈ R이 있어 A(±v2) = ±v2, A(±v3) = ±v3이 성립함을 의미한다.
따라서 A는 v = av1 + bv2 + cv3로 표현되는 벡터 v를 v' = (-av1) + bv2 + cv3으로 옮기는 선형사상이 된다.
그러므로 A는 벡터 v ∈ R에 수직한 평면에 대한 대칭변환이다.
같은 방법으로 B는 적당한 벡터 v ∈ R에 수직한 평면에 대한 대칭변환이다.
벡터 v, w가 이루는 각을 θ라고 하면, AB는 v, w에 수직인 직선은 고정시키고, v, w가 이루는 평면은 ±2θ만큼 회전이동을 시키는 변환이다.
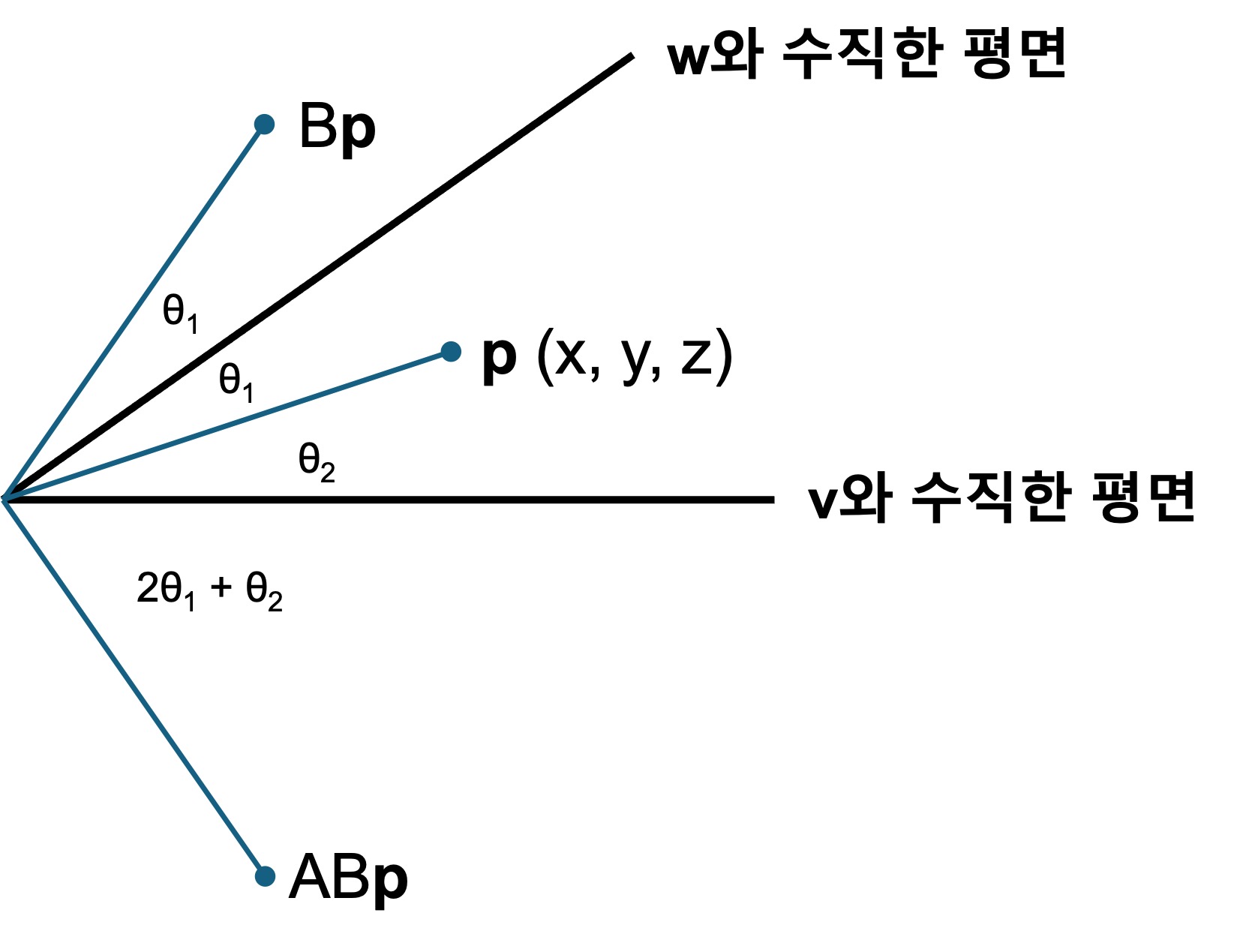
한편 R의 임의의 두 벡터가 이루는 각은
kπ/4 (k = 0, 1, 2, 3) 또는 lπ/3 (l = 0, 1, 2, 3)
이므로, 준 명제가 성립한다.
8. 실수에서 정의된 두 번 미분가능한 실함수 f가
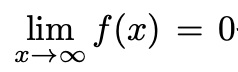
을 만족한다고 하자. 이때 다음 부등식이 성립함을 보여라.
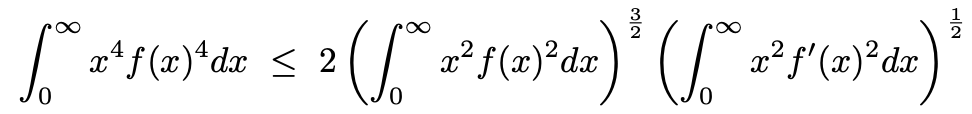
Solution.
대수경 공식 풀이를 참고하였다.
중간에 코시-슈바르츠 부등식(※)을 사용하였다.
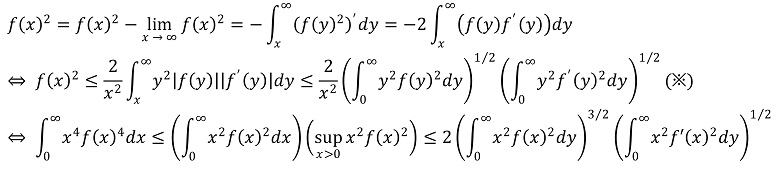
입력: 2024.04.05 09:14
수정: 2024.04.17 10:08
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 39회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2024.10.04 |
|---|---|
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.04.06 |
| 【대수경】 제 41회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.03.16 |
| 【대수경】 제 41회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.03.05 |
| 제 34회 전국 대학생 수학 경시대회 제 1 분야 #01 (0) | 2023.03.11 |




최근댓글