제 41회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 41회 전국 대학생 수학경시대회
제 2 분야
2023년 11월 11일 (10:30 - 13:30)
1. 좌표공간 안에 단위구 x2 + y2 + z2 = 1의 일부인 영역 D가 다음과 같이 주어졌다.

점 (0, 0, 1)에 놓인 광원(light source)으로부터 D를 xy-평면에 사영(projection)하여 얻은 영역의 넓이는 D의 넓이의 몇 배인지 구하여라.
Solution.

영역 D의 넓이는,

(cos ϕ cos θ, cos ϕ sin θ, sin ϕ)가 광원(0, 0, 1)과 (t cos ϕ cos θ, t cos ϕ sin θ, t(sin ϕ - 1) + 1), t ∈ ℝ의 직선의 방정식을 가지므로, t = 1 / (1 - sin ϕ)에서 x-y 평면에 직선과 교점이 생긴다.
즉, 정사영 영역 D*의 방정식은,
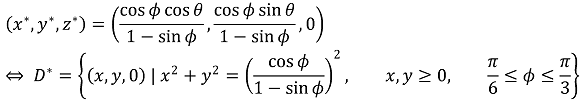
그런데,
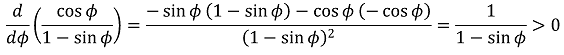
이므로 cos ϕ / (1 - sin ϕ)는 ϕ에 대하여 증가함수라 할 수 있어, 정사영 영역 D*의 넓이는,
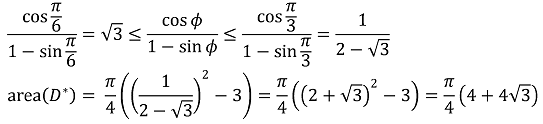
따라서, area (D*) / area (D) = (4 + 4√3) / (√3 - 1) = 4(2 + √3)
2. 다음 조건을 만족하는 열린 구간 (1/e, e)에서 정의된 함수 y = y(x)를 구하여라.

Solution.
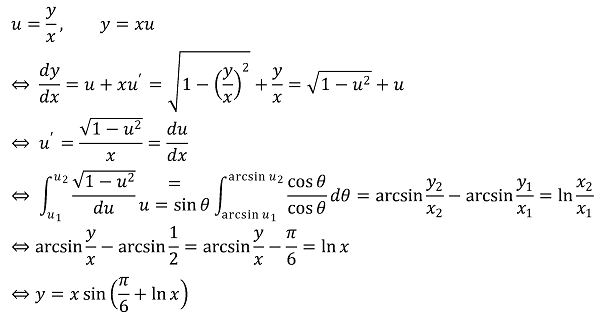
3. 함수 f(x) = exp(x8) sec(x4)에 대하여, f(16)(0) / 16!의 값을 구하여라. (단, f(n)(x)는 f(x)의 n계 도함수이다.)
Solution.
f(16)(x)는 다음과 같이 나타낼 수 있다.
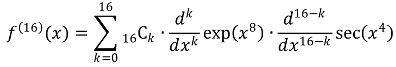
exp(x)의 매클로린 급수로부터, exp(x8)은 x = 0에서 다음과 같은 미분계수를 갖는다.
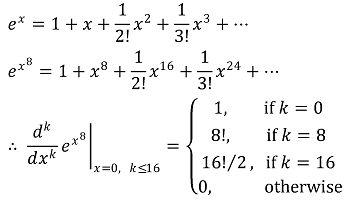
또한, d/dx sec(x) = sec(x)tan(x), d/dx tan(x) = sec2(x)로부터, x = 0에서 다음과 같은 미분계수들이 관찰된다.
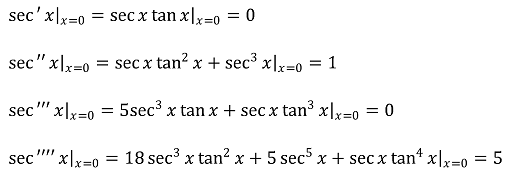
따라서 sec(x)와 sec(x4)는 다음과 같은 매클로린 급수를 갖는다.
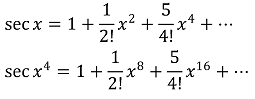
그러므로 (준식)은
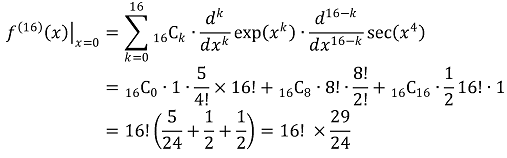
즉, 답은 29/24이다.
4. 크기가 2 × n (n ≥ 4)인 실행렬 A = (aij)와 순서쌍 (p, q)에 대하여
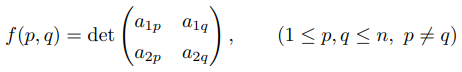
라고 하자.
⒜ 서로 다른 p, q, r, s에 대하여 다음이 성립함을 보여라.
f(p, q)f(r, s) = f(r, q)f(p, s) + f(s, q)f(r, p)
⒝ 임의의 q (2 ≤ q ≤ n)에 대하여 f(1, q) > 0이고 f(q-1, q) > 0임이 성립한다고 하자. 이때, 1 ≤ p < q ≤ n인 모든 순서쌍 (p, q)에 대하여 f(p, q) > 0임을 보여라.
Solution.
⒜
f(p, q)f(r, s) = (a1pa2q - a2pa1q)(a1ra2s - a2ra1s)
f(p, q)f(r, s) = a1pa2qa1ra2s - a2pa1qa1ra2s - a1pa2qa2ra1s + a2pa1qa2ra1s
f(r, q)f(p, s) = a1ra2qa1pa2s - a2ra1qa1pa2s - a1ra2qa2pa1s + a2ra1qa2pa1s
f(s, q)f(r, p) = a1sa2qa1ra2p - a1sa1qa1ra2p - a1sa2qa2ra1p + a2sa1qa2ra1p
⒝ 공식 풀이를 참고하였다.
q에 대한 수학적 귀납법을 적용한다.
먼저 q = 4인 경우를 생각하자.
f(1, 3)f(2, 4) = f(2, 3)f(1, 4) + f(4, 3)f(2, 1) = f(2, 3)f(1, 4) + f(3, 4)f(1, 2)
위 식에서 f(2, 4)를 제외한 나머지 f(p, q)는 양의 실수이므로 f(2, 4) > 0이 성립한다.
다음으로 4 ≤ q < n의 경우에 성립한다고 하자.
가정에 의해 1 < p < q인 q에 대하여 f(p, q+1) > 0이 성립함을 보이면 충분하다.
⒜에 의해
f(p, q+1)f(1, q) = f(1, q+1)f(p, q) + f(q, q+1)f(1, p)
이 성립하고, 가정에 의해 f(1, r) > 0 (r = p, q, q+1), f(p, q) > 0, f(q, q+1) > 0이 성립한다.
그러므로 위 식에 의하여 f(p, p+1) > 0이 성립한다.
5. 크기가 n × n인 실행렬 A에 대하여, det (A + D) ≠ 0이 성립하도록 하는 다음과 같은 꼴의 대각행렬 D가 존재함을 보여라.
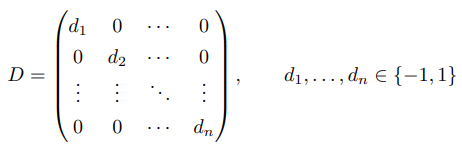
Solution. 공식 풀이를 참고하였다.
수학적 귀납법을 n에 대하여 사용하자.
먼저 n = 1일 때 A = (a)라고 두면, a + 1 또는 a - 1는 0이 아니므로, 주어진 명제는 사실이다.
이제, 주어진 명제가 n - 1에 대하여 사실임을 가정하고, 크기가 n × n인 실행렬 A을
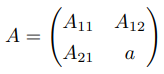
라고 두자. 여기서 A11는 크기가 (n - 1) × (n - 1)인 실행렬이고, a ∈ ℝ이다.
귀납 가정에 의해 크기가 (n - 1) × (n - 1)이면서 문제의 조건을 만족하는 대각행렬 E'이 존재하여 det (A11 + E') ≠ 0이 성립한다.
행렬식의 여인수 전개(cofactor expansion)로부터
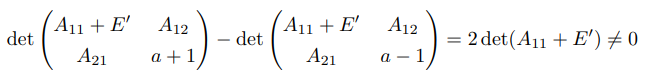
이 성립한다.
따라서, 처음 두 개의 행렬식 중 적어도 하나는 0이 아니게 되어, 명제가 n에 대해서도 성립한다.
6. A와 B가 바닥에서 출발하여 단의 개수가 12개인 계단을 먼저 올라가면 이기는 게임을 하려고 한다. 1부터 12까지의 수가 적혀있는 정12면체 주사위를 번갈아 던져서 다음의 규칙에 따라 계단을 올라간다.
○ A가 던져서 나온 주사위의 수가 4의 배수일 때, A는 4계단 올라간다.
○ B가 던져서 나온 주사위의 수가 6의 배수일 때, B는 6계단 올라간다.
○ 그 외의 경우에는 모두 움직이지 않는다.
A가 먼저 주사위를 던지기 시작할 때, A가 이길 확률을 구하여라. (단, 어느 한 명이 이길 때까지 계속하여 번갈아 주사위를 던진다.)
Solution.
A가 도달한 지점을 a, B가 도달한 지점을 b라고 하면 임의의 게임 상황을 순서쌍 (a, b)로 나타낼 수 있다.
A가 선공일 때, (a, b) → (a + 4, b)가 될 확률은 다음과 같다.
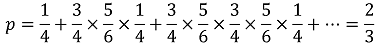
따라서 A가 선공일 때, (a, b) → (a, b + 6)이 될 확률은 다음과 같다.
p = 1 - 2/3 = 1/3
또한, A가 후공일 때, (a, b) → (a + 4, b)가 될 확률은 다음과 같다.
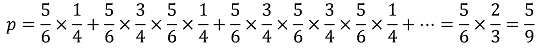
그리고 A가 후공일 때, (a, b) → (a, b + 6)이 될 확률은 다음과 같다.
p = 1 - 5/9 = 4/9
모든 게임 경우의 수는 다음 중 하나가 되는데, A가 승리하게 될 각 경로들에서 점화식처럼 적용하면 A가 승리하게 될 확률을 구할 수 있다. 단, A가 후공인 경우, 주황색 화살표로 표시하였다.
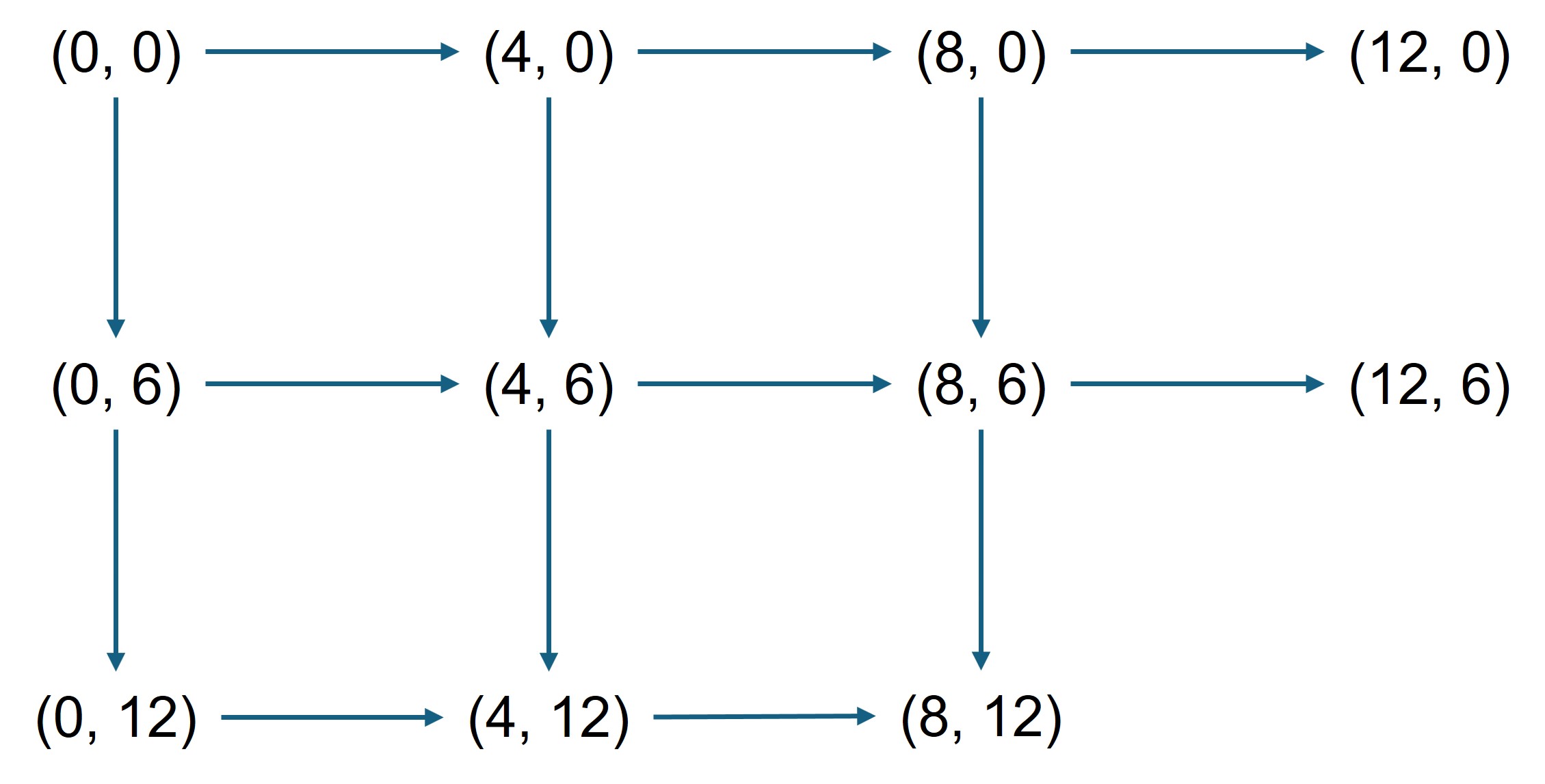
○ 경로 1. (0, 0) → (4, 0) → (8, 0) → (12, 0) : p = 2/3 × 5/9 × 5/9 = 50/243
○ 경로 2. (0, 0) → (4, 0) → (8, 0) → (8, 6) → (12, 6) : p = 2/3 × 5/9 × 4/9 × 2/3 = 80/729
○ 경로 3. (0, 0) → (4, 0) → (4, 6) → (8, 6) → (12, 6) : p = 2/3 × 4/9 × 2/3 × 5/9 = 80/729
○ 경로 4. (0, 0) → (0, 6) → (4, 6) → (8, 6) → (12, 6) : p = 1/3 × 2/3 × 5/9 × 5/9 = 50/729
답 : 50/243 + 80/729 + 80/729 + 80/729 + 50/729 = 40/81
7. 수열 {an}이 다음 식을 만족한다.
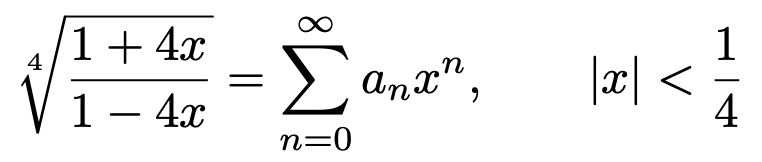
이때, 모든 n ≥ 0에 대하여 an은 음이 아닌 정수임을 보여라.
Solution.
⑴ 단계 1
준식에 대하여 n차 도함수를 취하면
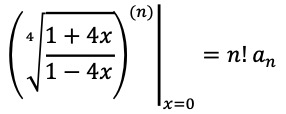
또한,
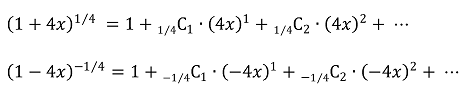
이므로, 이 둘의 곱으로부터 an이 될 수 있는 하나의 함수식을 얻을 수 있다.
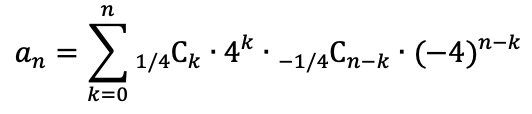
그런데 테일러 전개는 유일하므로 위 an의 형태가 an의 일반항이라고 할 수 있다.
이항계수의 정의를 이용하면 an이 분수라고 하더라도 분모의 소인수는 2밖에 없다는 것을 쉽게 증명할 수 있다.
예를 들어, 1/4C3 × 43 = 1/4 × (1/4 - 1) × (1/4 - 2) × 43 / 3! = (1 × (1-4) × (1-8)) / 6인데, 분자의 각 수(e.g., 1, -3, -7)는 분모의 각 수(e.g., 1, 2, 3)보다 절댓값이 큰 수들의 곱으로 구성되고 (사실 1), 홀수들과 서로소인 4라는 값으로 분자를 구성하는 각 홀수들이 spacing 돼 있어 (사실 2), 분자와 분모를 모두 소인수 분해한다면 분모에 있는 홀수인 소인수들은 모두 약분된다.
그러므로 분자의 각 수(e.g., 1, -3, -7)는 모두 홀수이고 분모에는 짝수(e.g., 2)가 있어서 an은 분모가 1, 2, 4, 8, ··· 중 하나라는 것만 알 수 있다.
그러므로 an > 0이고 an의 분모가 1, 2, 4, 8, ··· 중 1임을 증명해야 한다.
⑵ 단계 2
다음 관계식을 이용한다. (단, a0 = 1이다.)
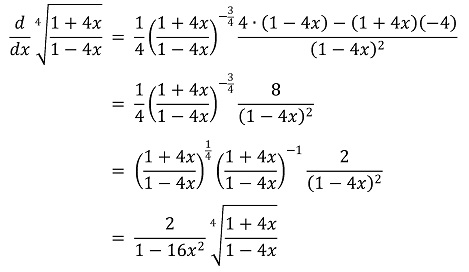
이로부터 다음 점화식을 얻을 수 있다.
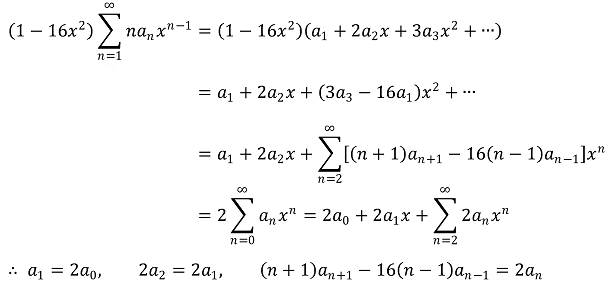
우선 (n+1)an+1 = 16(n-1)an-1 + 2an으로부터 an > 0임을 쉽게 알 수 있다.
a1, ···, a2k가 음이 아닌 정수라고 가정하면, a2k+1의 분모가 1, 2, 4, 8, ··· 중 하나임을 앎으로 a2k+1도 음이 아닌 정수이다.
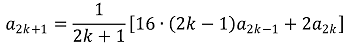
또한, a1, ···, a2k+1이 음이 아닌 정수라고 가정하면, a2k+3의 분모가 1, 2, 4, 8, ···임을 앎으로 16 × (2k+1) a2k+1 + 2a2k+2이 (2k+3)의 배수인 정수여야 하므로 a2k+2가 음이 아닌 정수임을 안다.
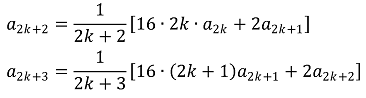
따라서, 점화식과 수학적 귀납법에 의해 an은 음이 아닌 정수이다.
입력: 2024.03.16 21:31
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.04.06 |
|---|---|
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 1 분야 (1) | 2024.04.06 |
| 【대수경】 제 41회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.03.05 |
| 제 34회 전국 대학생 수학 경시대회 제 1 분야 #01 (0) | 2023.03.11 |
| 【대수경】 제 34회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2023.03.11 |




최근댓글