제 41회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 41회 전국 대학생 수학경시대회
제 1 분야
2023년 11월 11일 (10:30 - 13:30)
1. 극좌표계에서 2 - 2 cos θ ≤ r ≤ 1을 만족하는 영역의 넓이를 구하라.
Solution.
영역은 다음과 같이 도출된다: θ = ± π/3에서 경계가 결정된다.

따라서 (준식)은,

2. 다음과 같이 크기가 2 × 2인 실행렬로 이루어진 벡터공간을 V라 하자.
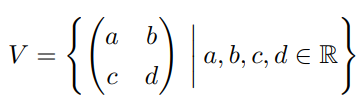
선형사상 T : V → V를 T(A) = At로 정의할 때, T의 고유값과 각 고유값에 대응하는 고유벡터를 모두 구하여라. (단, At는 A의 전치행렬)
Solution.
⑴ 출제 의도 : 다차원 벡터 대신 실행렬로 이루어진 벡터공간을 준 것으로 보아 선형대수학에 관한 수학적 센스를 검증하기 위함
⑵ 고유값 계산 : T(A) = λA로부터,
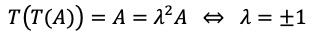
⑶ λ = 1인 경우 : T(A) = A로부터,
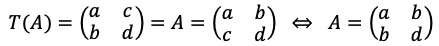
단, a, b, d는 모두가 0은 아닌 실수
⑷ λ = -1인 경우 : T(A) = -A로부터,
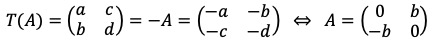
단, b는 0이 아닌 실수
3. 좌표평면에서 움직이는 점 X의 위치가 시각 t에 대하여 다음과 같은 매개함수로 표현된다.
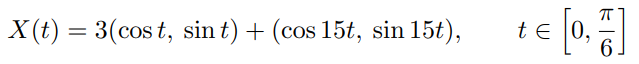
원점을 기준으로 점 X의 각도의 변화가 시계방향인 시각 t의 범위를 구하여라.
Solution.
X(t) 벡터보다 X(t) + X'(t) dt 벡터가 더 시계방향에 있음을 이용하자.
즉, X(t) × (X(t) + X'(t) dt) = X(t) × X'(t) dt (dt > 0) 벡터는 -z축 상에 있다. (단, X(t) 벡터는 3차원이라고 하자.)
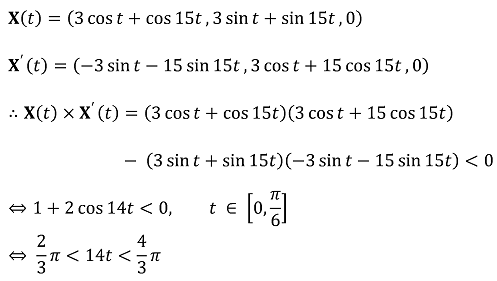
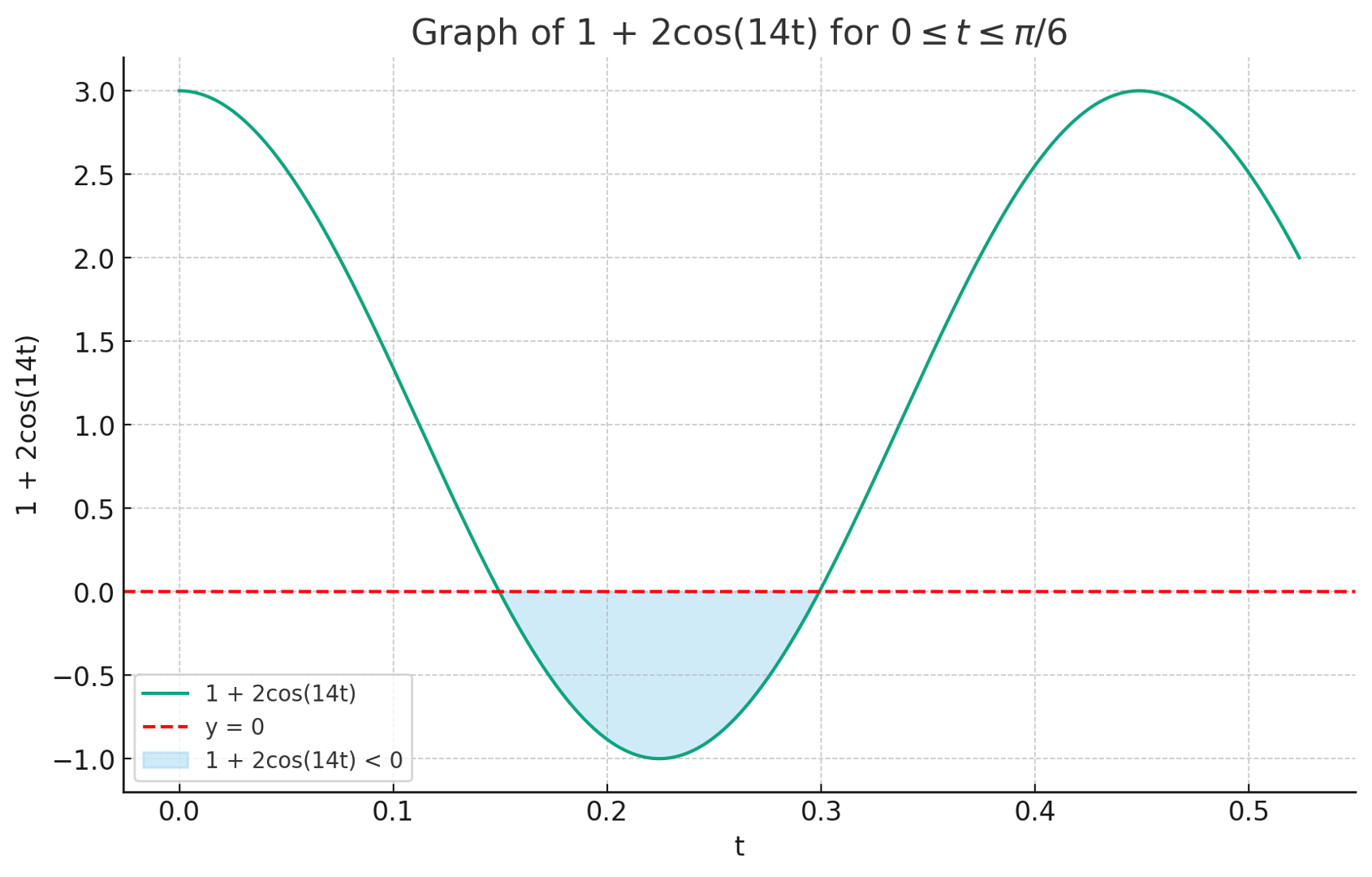
4. 집합 S = {2k | k는 음이 아닌 정수} = {1, 2, 4, 8, ···}라고 하자. 양의 정수 n을 S의 원소들의 합으로 표현하되, 같은 수는 최대 세 번까지만 사용하려고 한다. 이렇게 표현하는 방법의 개수를 f(n)이라 하자. 예를 들어, n = 7인 경우 다음과 같이 모두 네 가지 방법이 있으므로 f(n) = 4이다.
7 = 1 + 1 + 1 + 4 = 1 + 1 + 1 + 2 + 2 = 1 + 2 + 2 + 2 = 1 + 2+ 4
이때, f(n)을 n에 대한 식으로 표현하여라.
Solution.
풀이를 보면 답은 1 + ⎣n/2⎦라고 하지만, 필자 다음과 같이 f(n)을 푸는 게 타당하다고 생각한다.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| f(n) | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 4 | 6 | 6 | 6 | 6 | 8 | 8 | 5 | 5 |
기본적으로 양의 정수 n을 S의 원소들의 합으로 표현할 때, 필자는 내림차순으로 표현하였다. (e.g., 4 = 4 = 2 + 2 = 2 + 1 + 1)
이때 필자는 다음과 같은 점화식을 발견하였다.
점화식 : f(n) = f(n - 2k) + f(n - 2k-1) - f(n - 2k - 2k-1) (단, 2k ≤ n < 2k+1이고 k ≥ 0)
○ 정의 : 우선, f(0) = 1, f(ℤ-) = 0으로 정의한다.
○ f(n - 2k)의 의미 : 양의 정수 n을 S의 원소들의 합으로 표현했을 때, 최대 수가 2k인 경우를 지칭한다.
○ f(n - 2k-1)의 의미 : 원래 양의 정수 n을 S의 원소들의 합으로 표현했을 때, 최대 수가 2k-1인 경우를 의도했다. 그런데 2k-1 + 2k + ···와 같이 최대 수가 2k-1가 아닌 경우가 있다는 것을 알게 되었다. 심지어 내림차순도 아니다!
○ f(n - 2k - 2k-1)의 의미 : f(n - 2k-1)에서 2k-1 + 2k + ···와 같이 되는 경우를 빼기 위해 새로 도입하였다.
○ 위 점화식은 3회 조건이 만족하는 경우만을 필요충분적으로 잘 반영하고 있다.
○ 검토 1. n = 2k인 경우 위 점화식이 쉽게 성립함을 알 수 있고, n ≠ 2k인 경우 n < 2k-1 + 2k-1 + 2k-1 + 2k-1 ····이다. 따라서 2k ≤ n < 2k+1이라는 조건 자체가 3회 조건을 부분적으로 반영하고 있다.
○ 검토 2. 2k-2 + 2k-2 + (2k-2 + ··· ) ≤ 2k-2 + 2k-2 + (2k-1 -1) = 2k -1 < n이므로 3회 조건 하에서 점화식에서 2k-2 이하의 항으로만 구성된 경우를 고려할 필요는 없다.
예 1. n = 6인 경우
○ 22 ≤ 6 < 23이므로 k = 2
○ 6 = 4 + 2 = 4 + 1 + 1 = 2 + 2 + 2 = 2 + 2+ 1 + 1이므로 f(6) = 4
○ f(6 - 22) = 2와 대응되는 경우 : 4 + 2, 4 + 1 + 1
○ f(6 - 21) = 3과 대응되는 경우 : 2 + 4, 2 + 2 + 2, 2 + 2 + 1 + 1
○ f(6 - 22 - 21) = 1과 대응되는 경우 : 2 + 4
예 2. n = 10인 경우
○ 23 ≤ 10 < 24이므로 k = 3
○ 10 = 8 + 2 = 8 + 1 + 1 = 4 + 4 + 2 = 4 + 4 + 1 + 1 = 4 + 2 + 2 + 2 = 4 + 2 + 2 + 1 + 1이므로 f(10) = 6
○ f(10 - 23) = 2와 대응되는 경우 : 8 + 2, 8 + 1 + 1
○ f(10 - 22) = f(6) = 4와 대응되는 경우 : 4 + 4 + 2, 4 + 4 + 1 + 1, 4 + 2 + 2 + 2, 4 + 2 + 2 + 1 + 1
○ f(10 - 23 - 22) = f(-2) = 0과 대응되는 경우 : n = 10인 경우 2k-1 + 2k + ···인 경우 자체가 없는데, 이 경우 f(n - 2k - 2k-1) = f(-2) = 0이 되어 점화식 자체는 여전히 유효하게 성립한다.
그러나 이 경우 다음과 같은 패턴은 보이지만, 적당한 일반항을 찾을 수는 없었다.
○ f(2k) = k+1 (단, k ≥ 0) (∵ brute-force하게 탐색)
○ f(2k + 1) = f(1) + f(2k-1 + 1) = 1 + k (단, k ≥ 1) (∵ 수학적 귀납법)
○ f(2k + 2) = f(2) + f(2k-1 + 2) = 2 + 2(k-1) = 2k (단, k ≥ 2) (∵ 수학적 귀납법)
○ f(2k + 2k-1) = f(2k) + f(2k-1) - f(0) = (k+1) + k - 1 = 2k (단, k ≥ 1)
5. 다음 문제를 풀어라.
⒜ 크기가 n × n인 실행렬 A와 B에 대하여, 행렬 AB의 고윳값은 행렬 BA의 고유값이 됨을 증명하여라.
⒝ 홀수인 양의 정수 n에 대하여 크기가 n × n인 실행렬 A와 B가
2AB = (BA)2 + In
을 만족할 때, det (In - AB) = 0임을 보여라. (단, In은 크기가 n × n인 단위행렬)
Solution.
⑴ λ는 AB의 고유값이라고 가정
⇔ ABv = λv, v ≠ 0
⇔ BABv = BA (Bv) = B · λv = λ (Bv)
⇔ 다음과 같이 가능한 모든 경우를 고려해 보았을 때, BA의 고유값은 AB의 고유값과 동일함
① Bv ≠ O인 경우 : λ는 BA의 고유값
② Bv = O인 경우
⇔ ABv = AO = O = λv
⇔ λ = 0은 AB의 고유값
⇔ 0 = det(AB) = det(A) × det(B) = det(BA)
⇔ 따라서 BAv' = O인 v' ≠ 0이 존재함
⇔ λ = 0도 BA의 고유값
⑵ 문제 ⒜은 문제 ⒝를 풀 때 힌트가 됨
행렬 BA가 홀수 × 홀수 크기의 실행렬이므로 실수인 고유값이 존재한다: 예를 들어, 3 × 3 실행렬이라면, 모든 고유값들의 집합은 1개의 실수값, 3개의 실수값, 1개의 켤레 복소수 및 1개의 실수값 중 하나이다.
BA의 실수인 고유값을 λ, 고유벡터를 v ≠ 0이라고 하면, AB도 동일한 고유값 및 고유벡터를 가지므로
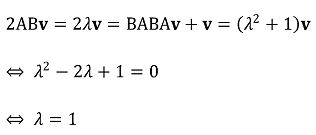
따라서 ABv = Inv ⇔ (In - AB)v = O (단, v ≠ 0)이 존재하므로 In - AB는 역행렬이 존재하지 않는다.
즉, det(In - AB) = 0
6. 양의 정수의 부분집합 S = {k | 1 ≤ k ≤ 2023, k와 2023은 서로소}에 대하여 N을 다음과 같이 정의하자.
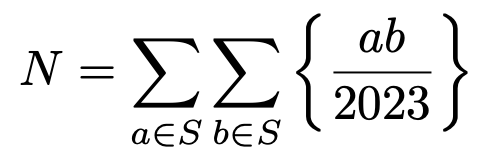
이때, N이 양의 정수임을 보이고 N을 소인수 분해 하여라. (단, {t} = t - [t]이고, [t]는 t 이하의 가장 큰 정수)
Solution.
⑴ N이 양의 정수임을 증명
2023 = 7 × 17 × 17
|S| = 2023 - 2023 / 7 - 2023 / 17 + 2023 / (7 × 17) = 1632 (∵ 포함배제의 원리)
∑k∈S k = 2023 × 816
N = ∑∑a,b ab/2023 - ∑∑a,b na,b = (2023 × 816)2 / 2023 - ∑∑a,b na,b = 정수
이때, na,b = [ab/2023]을 의미한다. (단, [t]는 t 이하의 가장 큰 정수)
N > 0임은 자명하므로 N은 양의 정수이다.
⑵ 예 1. 2023 대신 7일 때, ∑a,b na,b를 계산하는 과정
| b \ a | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 |
Table. 1. 2023 대신 7인 상황에서 a × b를 나타낸 과정
na,b 값에 따라서 음영을 달리 하였음
S = S = {k | 1 ≤ k ≤ 7, k와 7은 서로소}이라면, |S| = 6, Σk∈S k = 21이 성립한다.
Σna,1 + ··· + Σna,6 = 0 + 3 + 6 + 9 + 12 + 15 = 6 / 2 × (21 - 6) = 45
⑶ 예 2. 2023 대신 9일 때, ∑a,b na,b를 계산하는 과정
| b \ a | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 |
Table. 2. 2023 대신 9인 상황에서 a × b를 나타낸 과정
na,b 값에 따라서 음영을 달리 하였고, a와 b가 9와 서로소가 아니면 검은색 음영으로 하였음
S = S = {k | 1 ≤ k ≤ 9, k와 9은 서로소}이라면, |S| = 6, Σk∈S k = 27이 성립한다.
Σna,1 + Σna,2 + Σna,4 + Σna,5 + Σna,7 + Σna,8 = 0 + 3 + 9 + 12 + 18 + 21 = 6 / 2 × (27 - 6) = 63
⑷ 결론 : 2023으로 계산을 하는 과정 : 사실 이 과정을 수학적 귀납법으로 엄밀하게 보일 수도 있다.
S = S = {k | 1 ≤ k ≤ 2023, k와 2023은 서로소}이라면, |S| = 1632, Σk∈S k = 2023 × 816이 성립한다.
Σna,1 + ··· + Σna,2022 = 1632 / 2 × (2023 × 816 - 1632) = 8162 (2023 - 2)
∴ N = ∑∑a,b ab/2023 - ∑∑a,b na,b = 2023 × 8162 - 8162 (2023 - 2) = 8162 × 2 = 29 × 32 × 172
7. 수열 {an}이 다음 식을 만족한다.
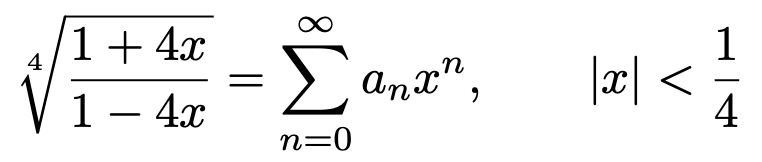
이때, 모든 n ≥ 0에 대하여 an은 음이 아닌 정수임을 보여라.
Solution.
⑴ 단계 1
준식에 대하여 n차 도함수를 취하면
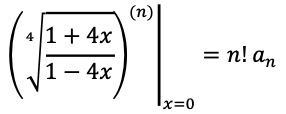
또한,
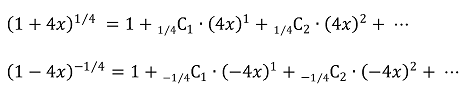
이므로, 이 둘의 곱으로부터 an이 될 수 있는 하나의 함수식을 얻을 수 있다.
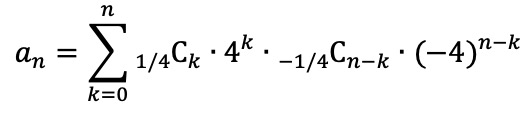
그런데 테일러 전개는 유일하므로 위 an의 형태가 an의 일반항이라고 할 수 있다.
이항계수의 정의를 이용하면 an이 분수라고 하더라도 분모의 소인수는 2밖에 없다는 것을 쉽게 증명할 수 있다.
예를 들어, 1/4C3 × 43 = 1/4 × (1/4 - 1) × (1/4 - 2) × 43 / 3! = (1 × (1-4) × (1-8)) / 6인데, 분자의 각 수(e.g., 1, -3, -7)는 분모의 각 수(e.g., 1, 2, 3)보다 절댓값이 큰 수들의 곱으로 구성되고 (사실 1), 홀수들과 서로소인 4라는 값으로 분자를 구성하는 각 홀수들이 spacing 돼 있어 (사실 2), 분자와 분모를 모두 소인수 분해한다면 분모에 있는 홀수인 소인수들은 모두 약분된다.
그러므로 분자의 각 수(e.g., 1, -3, -7)는 모두 홀수이고 분모에는 짝수(e.g., 2)가 있어서 an은 분모가 1, 2, 4, 8, ··· 중 하나라는 것만 알 수 있다.
그러므로 an > 0이고 an의 분모가 1, 2, 4, 8, ··· 중 1임을 증명해야 한다.
⑵ 단계 2
다음 관계식을 이용한다. (단, a0 = 1이다.)
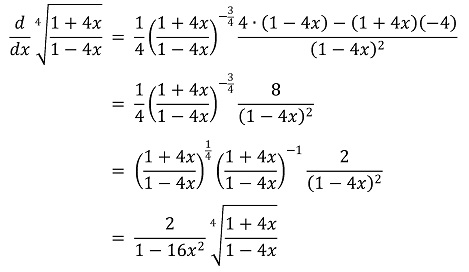
이로부터 다음 점화식을 얻을 수 있다.
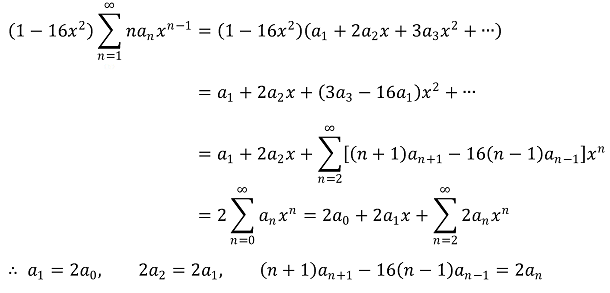
우선 (n+1)an+1 = 16(n-1)an-1 + 2an으로부터 an > 0임을 쉽게 알 수 있다.
a1, ···, a2k가 음이 아닌 정수라고 가정하면, a2k+1의 분모가 1, 2, 4, 8, ··· 중 하나임을 앎으로 a2k+1도 음이 아닌 정수이다.
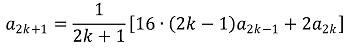
또한, a1, ···, a2k+1이 음이 아닌 정수라고 가정하면, a2k+3의 분모가 1, 2, 4, 8, ···임을 앎으로 16 × (2k+1) a2k+1 + 2a2k+2이 (2k+3)의 배수인 정수여야 하므로 a2k+2가 음이 아닌 정수임을 안다.
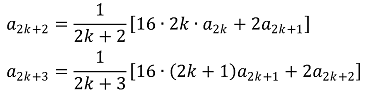
따라서, 점화식과 수학적 귀납법에 의해 an은 음이 아닌 정수이다.
입력: 2024.03.05 00:49
수정: 2024.03.16 21:26
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 1 분야 (1) | 2024.04.06 |
|---|---|
| 【대수경】 제 41회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.03.16 |
| 제 34회 전국 대학생 수학 경시대회 제 1 분야 #01 (0) | 2023.03.11 |
| 【대수경】 제 34회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2023.03.11 |
| 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음 (0) | 2022.03.06 |




최근댓글