제 34회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 34회 전국 대학생 (공업)수학 경시대회
제 2 분야
2015년 11월 14일 (10:00 - 13:00)
1. 다음 적분값을 계산하여라.

Solution.
u = x2 + 1이라고 두자.

2. 양의 정수 n에 대하여 크기가 n × n인 행렬 A = (aij)가 aij = max{ i, j }로 주어질 때, det (A)를 구하여라.
Solution.
⑴ 1 × 1 행렬, 2 × 2 행렬, 3 × 3 행렬에 대한 조사

⑵ 행렬식의 성질

⑶ 수학적 귀납법 적용

3. 급수
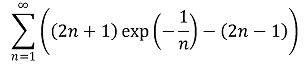
의 수렴 여부를 판정하여라.
Solution.
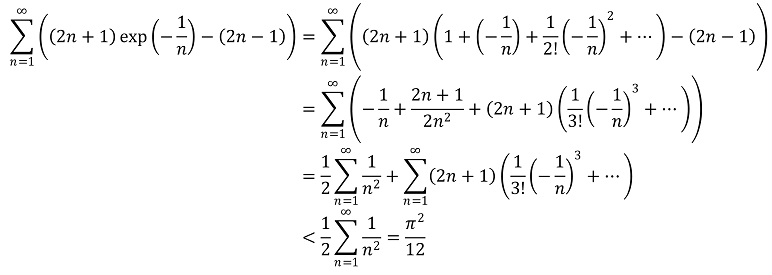
완비성 공리에 의해, 증가수열이 유계이면 그 수열은 수렴한다.
4. 모든 성분이 유리수이고 크기가 5 × 5인 행렬 A의 한 고유벡터가 (1, √2, √3, √4, √5)T이다. 이 때, AT는 모든 성분이 유리수인 고유벡터를 가짐을 보여라. (단, AT는 A의 전치행렬)
Solution.
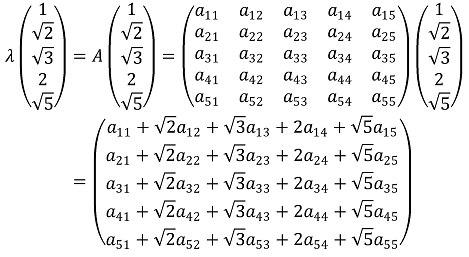
√2, √3, √5는 유리수의 연산에 대하여 선형 독립이다.
그런데 A의 모든 성분은 유리수라고 주어져 있다.
따라서 1행과 4행을 비교만 해도 다음과 같은 관계식을 찾을 수 있다.
2 × (a11 + 2a14) = a41 + 2a44
2 × a12 = a42
2 × a13 = a43
2 × a15 = a45
따라서 다음과 같은 고유벡터가 있음을 보일 수 있다.
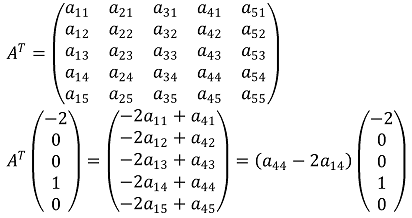
5. 무한 번 미분가능한 함수 f : (-1, ∞) → ℝ가 모든 양의 정수 n에 대하여, f(1/n) = n / (n+1)을 만족할 때 f'''(0)을 구하여라.
Solution.
주어진 함수는 무한 번 미분가능하므로, 연속임은 자명하다.
n이 상당히 클 때, 함수의 연속에 의해 1/n에 수렴하는 실수열 { xm }은 다음을 만족한다.
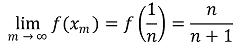
따라서 x = 0+ 근처에서 f(x) = (1/x) / ((1/x) + 1) = 1/(x+1)을 만족한다고 볼 수 있다. (함수 근사)
그러므로 f'''(0)은 다음과 같다.
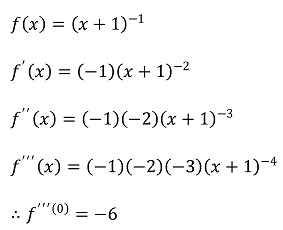
6. 함수 f : [a, b] → ℝ가 연속일 때, 다음을 만족하는 상수 c ∈ [a, b]가 존재함을 보여라.
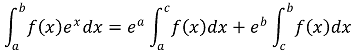
Solution.
c = a인 경우 다음이 성립한다.
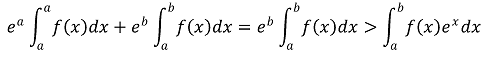
c = b인 경우 다음이 성립한다.
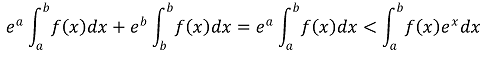
따라서, 중간값 정리에 의해 (준식)을 만족하는 c ∈ [a, b]가 존재한다.
7. 양의 정수 n에 대하여 크기가 n × n인 복소행렬 A = (aij)가 다음 조건을 만족한다.
(i) aii = 1 (1 ≤ i ≤ n)
(ii) aij = 0 (1 ≤ j < i ≤ n)
(iii) ĀA = I
이 때, 다음 조건을 만족하는 크기가 n × n인 복소행렬 B = (bij)가 존재함을 보여라.
(I) bii = 1 (1 ≤ i ≤ n)
(II) bij = 0 (1 ≤ j < n)
(III) B̅A = B
(단, Ā = (āij), I는 단위행렬)
Solution.
실수부가 1/2인 임의의 복소수 α에 대하여 B = αA + αI는 주어진 조건을 만족함을 알 수 있다.
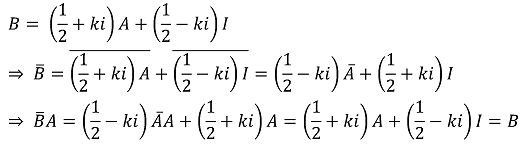
8. 양의 정수 n에 대하여 크기가 n × n인 실행렬 X = (xij)의 성분 xij들은 X가 가역인 범위에 있다고 가정하자. 역행렬 Y = X-1 = (ypq)의 성분을
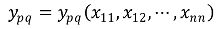
과 같이 변수 xij에 대한 함수로 생각할 때, 다음을 보여라.
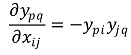
Solution.
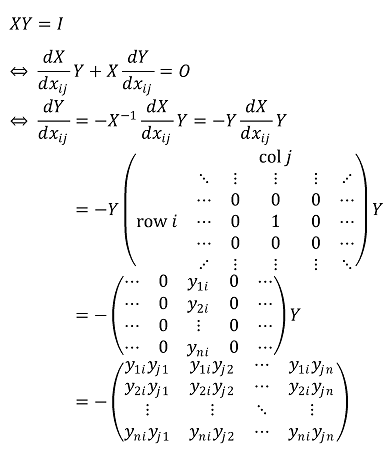
입력: 2023.03.11 10:53
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 41회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.03.05 |
|---|---|
| 제 34회 전국 대학생 수학 경시대회 제 1 분야 #01 (0) | 2023.03.11 |
| 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음 (0) | 2022.03.06 |
| 제 26회 전국 대학생 수학 경시대회 제 1 분야 #01-05 (0) | 2016.06.26 |
| 제 26회 전국 대학생 수학 경시대회 제 1 분야 #01-04 (0) | 2016.06.26 |




최근댓글