제 40회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 40회 전국 대학생 수학경시대회
제 2 분야
2021년 11월 13일 (10:00 - 11:30)
1. 다음 극한값을 구하여라.

Solution.

2. 다음 미분방정식의 해를 구하여라.

Solution.

라 정의하면, 다음을 얻을 수 있다.
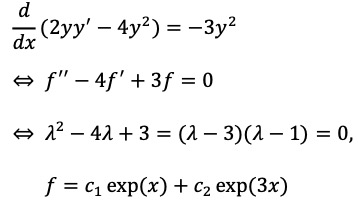
f'(0) = y(0)2 = 4 = c1 exp(0) + 3c2 exp(0) = c1 + 3c2,
f''(0) = 2y(0)y'(0) = 12 = c1 exp(0) + 9c2 exp(0) = c1 + 9c2
이므로 c1 = 0, c2 = 4/3을 얻을 수 있다.
즉, y2 = 4 exp(3x)이므로 y(x) = 2 exp(1.5x)를 얻는다.
3. 다음 행렬이 가역행렬이 되도록 하는 2 이상의 정수 n과 실수 α1, ···, αn, β1, ···, βn을 모두 구하여라.
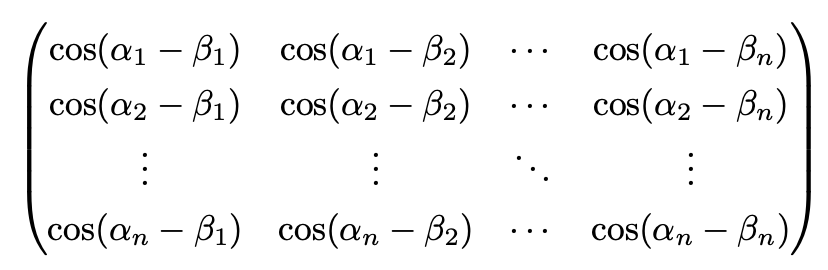
Solution. 공식 풀이를 참고하였다.
등식 cos (x - y) = cos x cos y + sin x sin y로부터, 문제의 행렬은
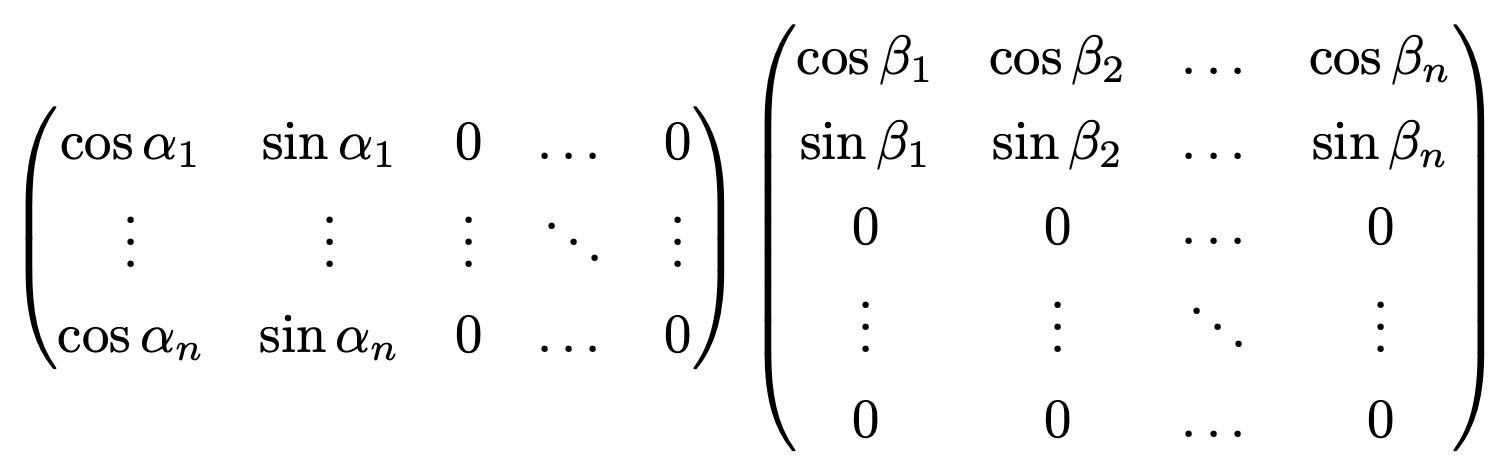
와 같이 두 행렬의 곱으로 쓸 수 있다.
따라서 n ≥ 3이면 주어진 행렬은 항상 비가역이다.
n = 2일 때, 주어진 행렬의 행렬식은 다음과 같다.
sin (α2 - α1) sin (β2 - β1)
따라서 주어진 행렬이 가역이기 위한 필요충분조건은, n = 2이고 α2 - α1과 β2 - β1이 모두 π의 정수배가 아닌 것이다.
4. 영역 D = {(x, y) ∈ ℝ2 : x > 0, y > 0, 1 - x - y > 0 }에서 함수 f : D → ℝ을 다음과 같이 정의하자.
f(x, y) = 4(x2 + y2 + (1 - x - y)2) - x log x - y log y - (1 - x - y) log (1 - x - y)
이때 f의 극점(critical point)의 개수를 구하여라.
Solution.
f의 극점 (x, y)는 다음 조건을 만족하는 점이다.
∂f / ∂x = 16x + 8y - 8 - log x + log (1 - x - y) = 0
∂f / ∂y = 16y + 8x - 8x - log y + log (1 - x - y) = 0
이제 극점의 개수를 구하기 위해 시각적으로 문제를 풀어보자.
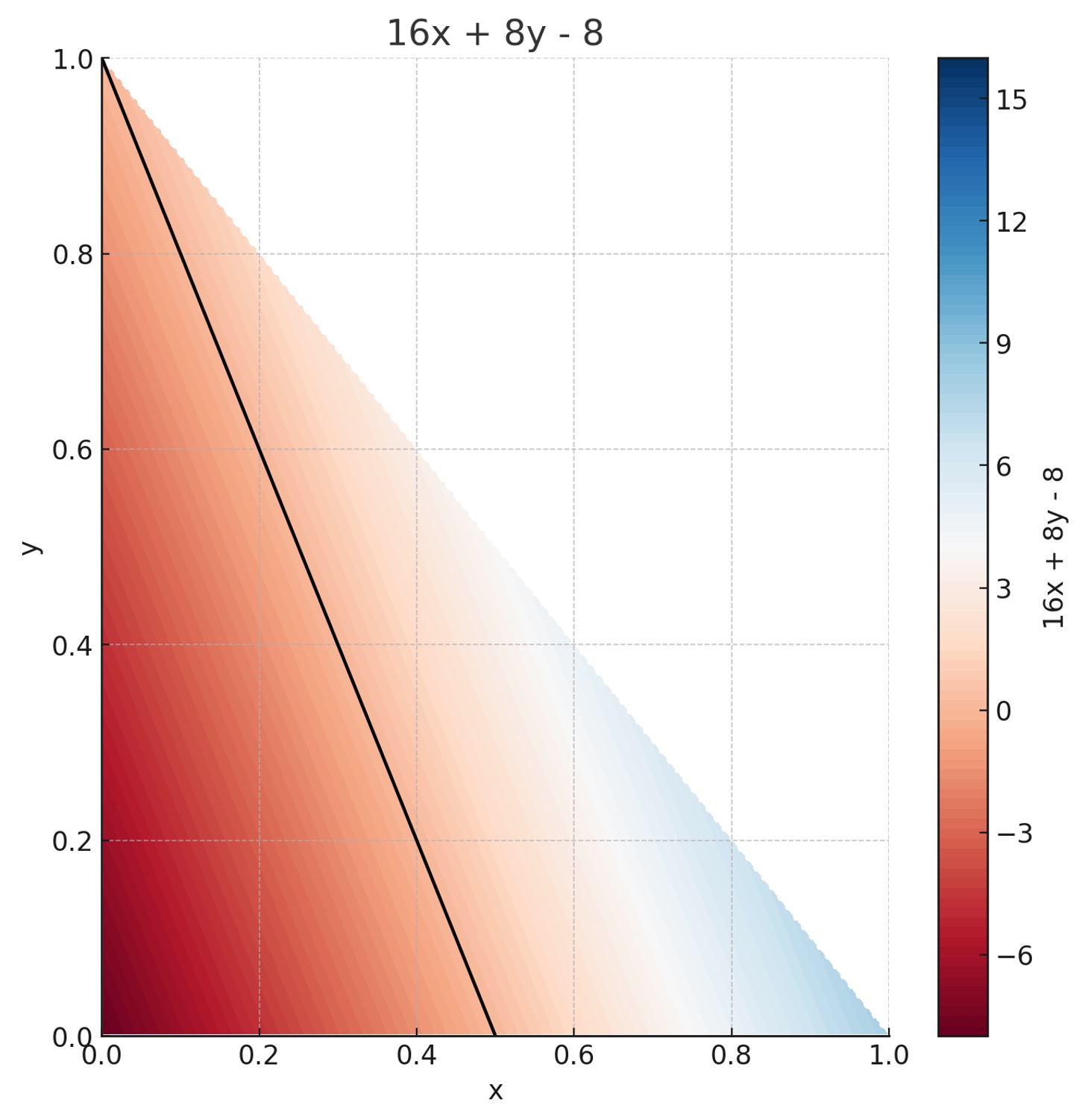
우선 영역 D에서 16x + 8y - 8 값의 분포는 다음과 같다. (단, 값이 0인 부분은 검정색 선으로 표시했다.)
import numpy as np
import matplotlib.pyplot as plt
# Create a grid of points
x = np.linspace(0, 1, 500)
y = np.linspace(0, 1, 500)
X, Y = np.meshgrid(x, y)
Z = 16*X + 8*Y - 8
# Mask the region outside the defined area for Z
Z_masked = np.ma.masked_where((1 - X - Y) <= 0, Z)
# Create the plot
plt.figure(figsize=(8, 8))
cp = plt.contourf(X, Y, Z_masked, levels=np.linspace(Z_masked.min(), Z_masked.max(), 500), cmap='RdBu')
plt.contour(X, Y, Z_masked, levels=[0], colors='black') # Add contour line for Z=0
# Create a colorbar with a label
plt.colorbar(cp, label='16x + 8y - 8')
# Add titles and labels
plt.title('16x + 8y - 8')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.show()
그리고 영역 D에서 16x + 8y - 8 - log x 값의 분포는 다음과 같다. (단, 값이 0인 부분은 검정색 선으로 표시했다.)
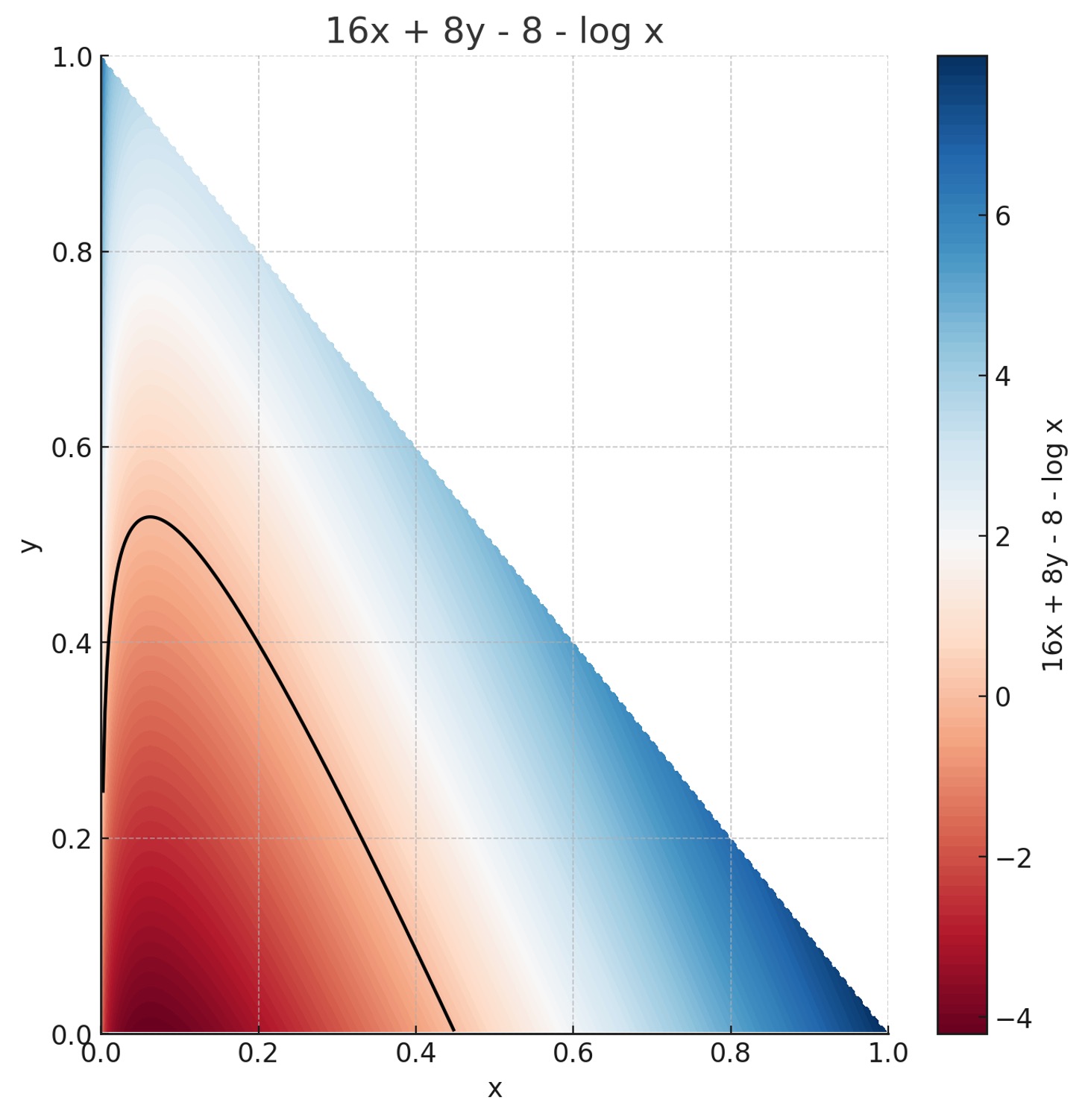
또한, 영역 D에서 16x + 8y - 8 - log x + log (1 - x - y) 값의 분포는 다음과 같다. (단, 값이 0인 부분은 검정색 선으로 표시했다.)
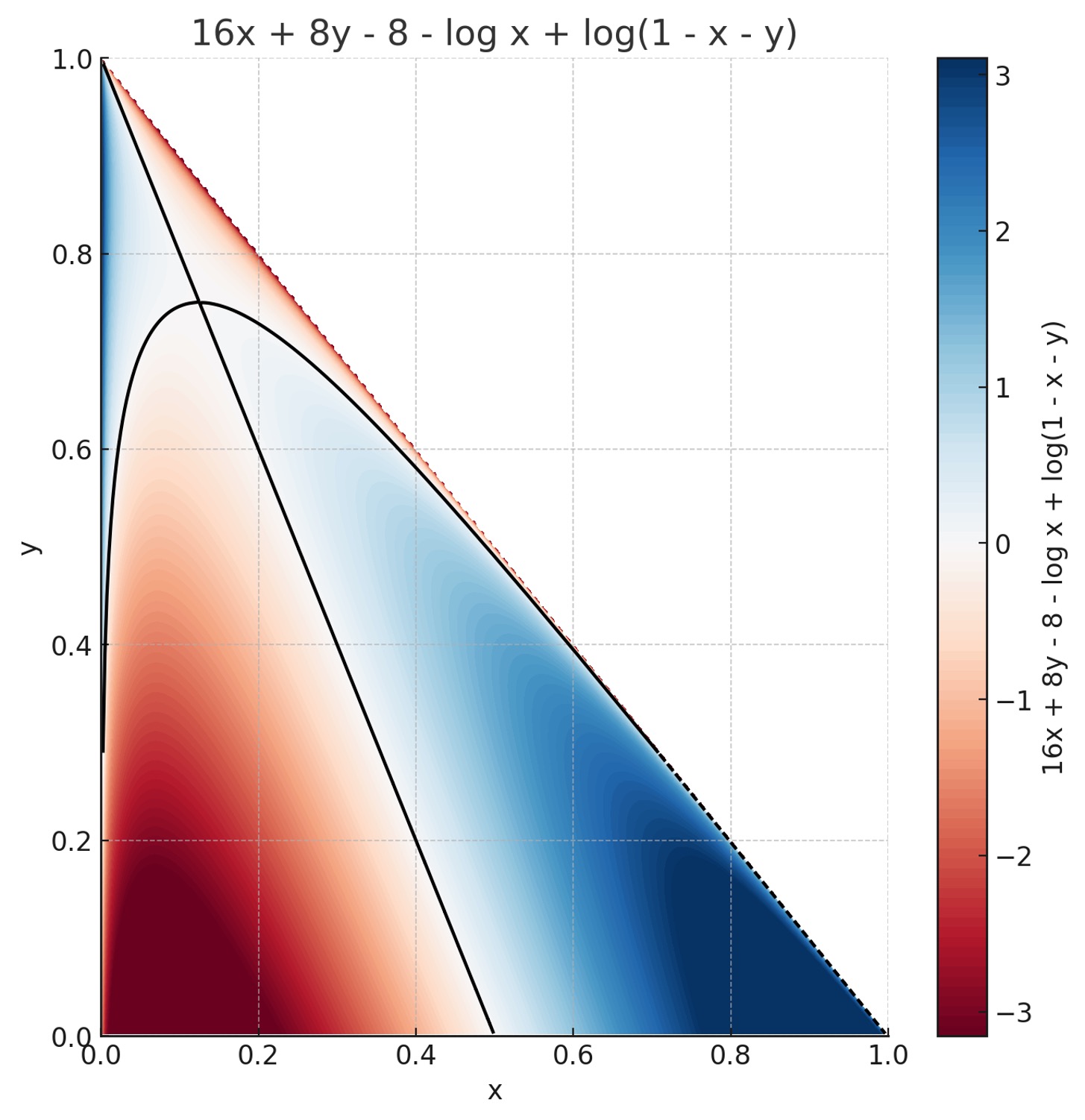
위 그림에서 검정색 선은 ∂f / ∂x = 0인 (x, y)를 나타낸다.
∂f / ∂y = 0은 위 선을 y = x에 대해 대칭적으로 나타낸 집합이다.
따라서 f의 극점 (x, y)는 ∂f / ∂x = 0인 선과 ∂f / ∂y = 0인 선의 교점이므로 다음과 같이 시각적으로 나타낼 수 있다.
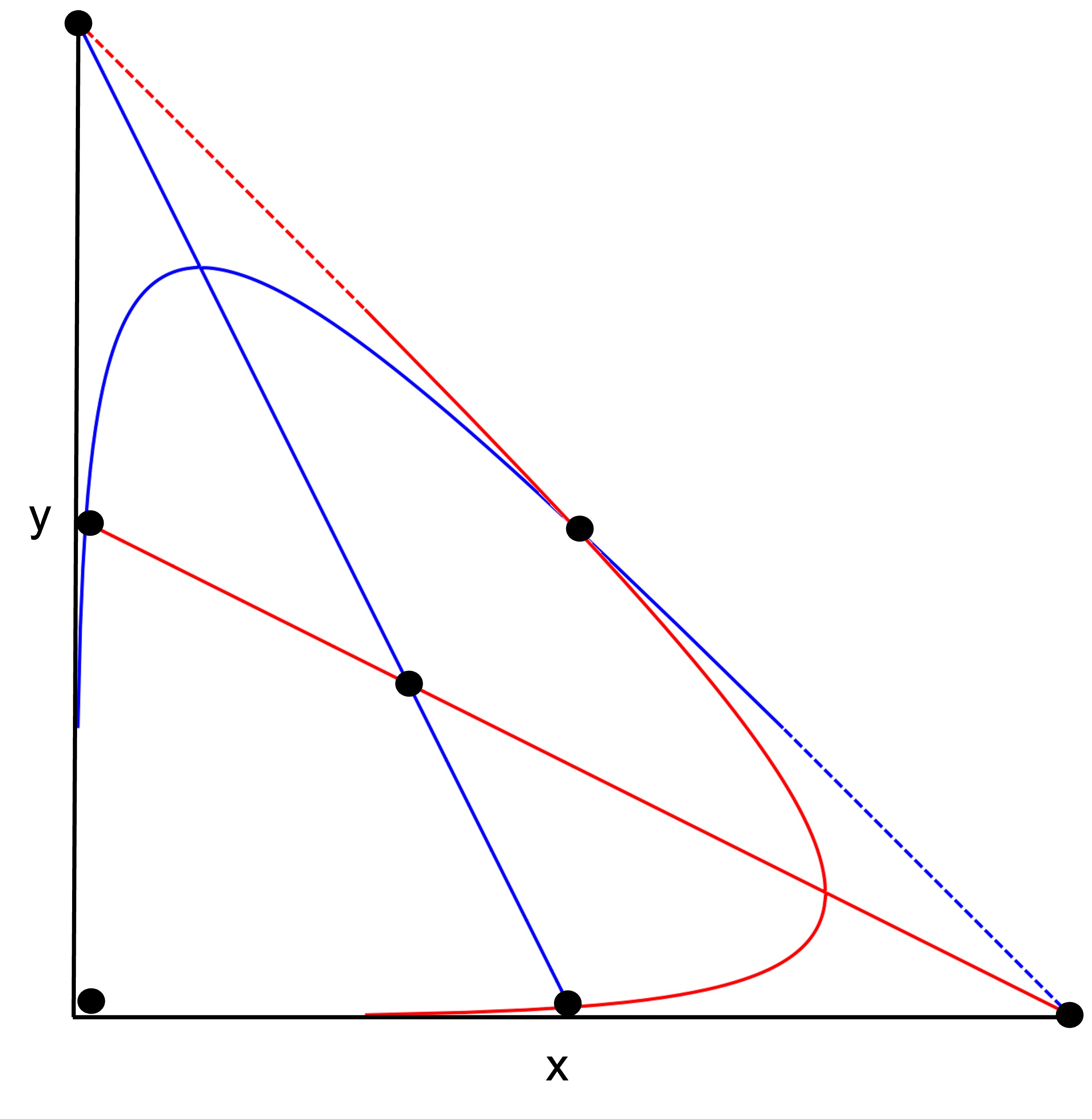
그러므로 f의 극점의 개수는 7개이다.
5. 다음 적분값을 구하여라.
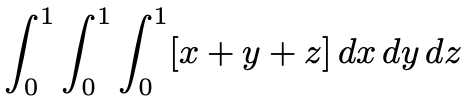
(단, [t]는 실수 t를 넘지 않는 가장 큰 정수이다.)
Solution.
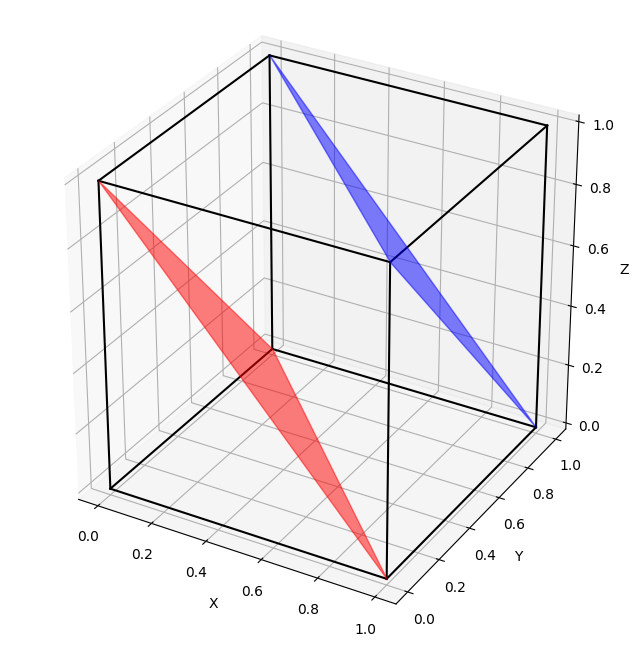
영역 D* = {(x, y, z) ∈ ℝ3 : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1}와 x + y + z = 1 (빨강), x + y + z = 2 (파랑)을 나타내면 다음과 같다.
from itertools import product, combinations
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
# Set up the figure and axis
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
# Draw the cube
r = [0, 1]
for s, e in combinations(np.array(list(product(r, r, r))), 2):
if np.sum(np.abs(s - e)) == r[1]-r[0]:
ax.plot3D(*zip(s, e), color="k")
# x + y + z = 1 plane triangle vertices
vertices = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
triangle = Poly3DCollection([vertices], alpha=0.5, color='red')
ax.add_collection3d(triangle)
# x + y + z = 1 plane triangle vertices
vertices = np.array([[1, 1, 0], [0, 1, 1], [1, 0, 1]])
triangle = Poly3DCollection([vertices], alpha=0.5, color='blue')
ax.add_collection3d(triangle)
# Labeling the axes
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Setting the aspect ratio to 'auto' for equal scaling
ax.set_box_aspect([1,1,1]) # Aspect ratio is 1:1:1
plt.show()
빨간색 평면에서 원점 방향으로 이동하면, [x + y + z] = 0이다.
빨간색 평면과 파란색 평면 사이에서 [x + y + z] = 1이다.
그리고 파란색 평면에서 (1, 1, 1) 방향으로 이동하면 [x + y + z] = 2이다.
그러므로 (준식)은
(준식) = 1 × 평면 간 사이 부피 + 2 × 파란색 평면이 밑면인 삼각뿔 = 1 × (13 - 1/3 × 1/2 × 1 × 2) + 2 × (1/3 × 1/2 × 1) = 1
6. 크기가 n × n인 가역행렬 A = (aij)가 1 ≤ k ≤ n인 모든 정수 k에 대하여 다음을 만족한다.
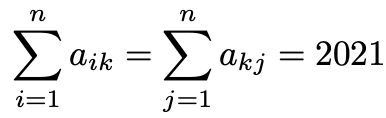
행렬 A의 역행렬을 B = (bij)라 할 때, 1 ≤ k ≤ n인 모든 정수 k에 대하여 다음이 성립함을 보여라.
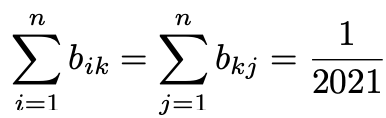
Solution.
BA = I의 i행 j번째 성분은 다음과 같이 나타난다.
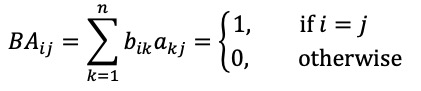
B의 i 번째 행벡터를 βi, A의 j 번째 열벡터를 αj라 할 때, BAi1 + ··· + BAin = 1로부터 다음을 얻을 수 있다. - (※)
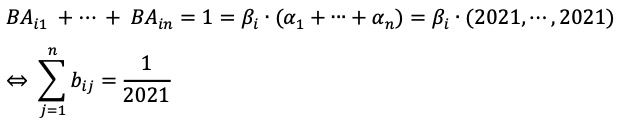
BA = I 대신 AB = I라는 사실을 이용하면, 임의의 k에 대하여 b1k + ··· + bnk = 1라는 사실도 쉽게 보일 수 있다.
물론, 대칭성의 원리에 의해 그러한 사실을 보이지 않아도 (※)로부터 준 명제가 자명하게 성립한다.
7. 실수 a, b에 대하여 행렬 A를 다음과 같이 정의하자.
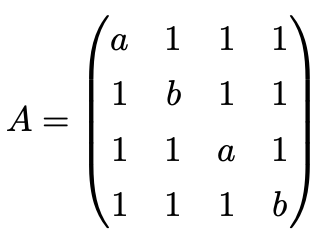
이때 행렬 A가 양의 정부호(positive definite)일 필요충분조건은 a > 1이고 b > 1임을 보여라.
Solution.
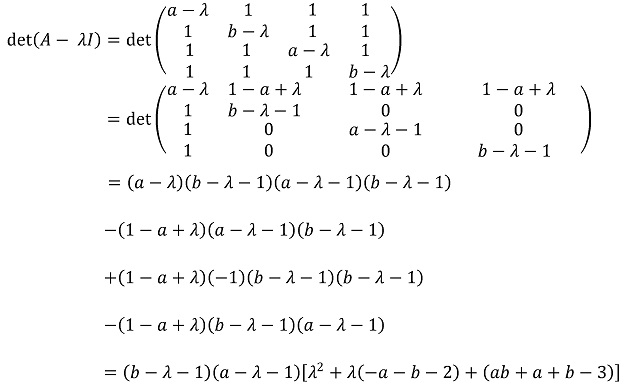
정방향 증명
행렬 A가 양정부호 행렬이라면, λ1 = b - 1 > 0, λ2 = a - 1 > 0이 성립한다.
역방향 증명
a > 1, b > 1이라면, λ2 + λ(-a - b - 2) + (ab + a + b - 3) = 0의 두 해 λ3, λ4는 λ3 + λ4 = a + b + 2 > 0, λ3λ4 = (a+1)(b+1) - 4 > 0으로부터 λ3 > 0, λ4 > 0이 성립한다.
λ1 = b - 1 > 0, λ2 = a - 1 > 0이 성립하므로 행렬 A는 양정부호 행렬이다.
그러므로 준명제가 성립한다.
8. 실수에서 정의된 두 번 미분가능한 실함수 f가
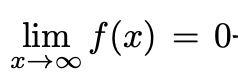
을 만족한다고 하자. 이때 다음 부등식이 성립함을 보여라.
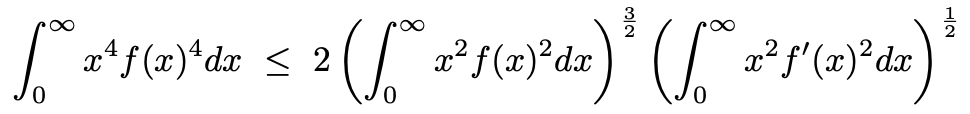
Solution.
대수경 공식 풀이를 참고하였다.
중간에 코시-슈바르츠 부등식(※)을 사용하였다.
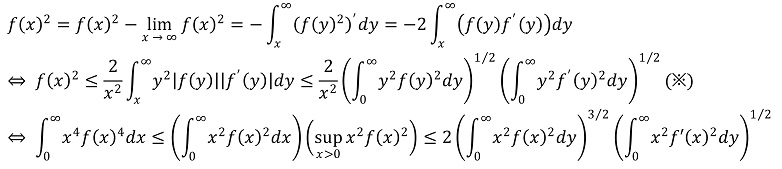
입력: 2024.04.06 01:28
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 39회 전국 대학생 수학 경시대회 제 2 분야 (4) | 2024.12.06 |
|---|---|
| 【대수경】 제 39회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2024.10.04 |
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 1 분야 (1) | 2024.04.06 |
| 【대수경】 제 41회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.03.16 |
| 【대수경】 제 41회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.03.05 |




최근댓글