제 39회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 39회 전국 대학생 수학경시대회
제 1 분야
2020년 11월 14일 (10:00 - 11:30)
1. 다음 극한값을 구하여라.

Solution.
ex = 1 + x + x2 / 2! + x3 / 3! + ···
sin(x) = x - x3 / 3! + x5 / 5! - ···
sin(x2) = x2 - x6 / 3! + x10 / 5! - ···
∴ ex·sin(x2) = x2 + x3 + x4 / 2! + x5 / 3! + ···
∴ ex·sin(x2) - x2 = x3 + x4 / 2! + x5 / 3! + ···
∴ (준식) = 1
2. 양의 정수 n은 완전제곱수이고, 마지막 네 자리의 숫자가 모두 같다. 이때, n은 10000의 배수임을 보여라.
Solution.
완전제곱수를 8로 나눈 나머지는 0, 1, 4 중 하나이다.
n = m2이라고 할 때,
m의 끝자리가 0인 경우 : 마지막 네 자리의 숫자는 0000
m의 끝자리가 1, 9인 경우 : 마지막 네 자리의 숫자는 1111 → 8로 나눈 나머지가 7이므로 모순
m의 끝자리가 2, 8인 경우 : 마지막 네 자리의 숫자는 4444
m의 끝자리가 3, 7인 경우 : 마지막 네 자리의 숫자는 9999 → 8로 나눈 나머지가 7이므로 모순
m의 끝자리가 4, 6인 경우 : 마지막 네 자리의 숫자는 6666 → 8로 나눈 나머지가 2이므로 모순
m의 끝자리가 5인 경우 : 마지막 네 자리의 숫자는 5555 → 8로 나눈 나머지가 3이므로 모순
n의 마지막 네 자리의 숫자가 4444인 경우, n = 4k = m2으로 둘 수 있다.
따라서 k = (m / 2)2이므로 k도 또한 제곱수이다.
k의 마지막 네 자리의 숫자 1111을 8로 나눈 나머지가 7이므로 모순이다.
따라서, n의 마지막 네 자리의 숫자는 0000이다.
즉, n은 10000의 배수이다.
3. 크기가 n × n이고 영행렬이 아닌 실대칭행렬 Z는 tr(Z) ≤ 0을 만족한다. 이때, 충분히 큰 모든 양의 정수 k에 대하여 다음 부등식이 성립함을 보여라. (단, In은 크기가 n × n인 단위 행렬이다.)

Solution.
k가 꼭 양의 정수일 필요는 없고, 양의 실수여도 결론은 동일하다.
경우 1. tr(Z) ≠ 0이라고 가정하자.
임의의 n × n 행렬 A의 행렬식 det A는 다음과 같이 정의된다. (단, σ는 치환이다.)

k가 충분히 크면 (1/k) Z의 모든 성분이 모두 0에 매우 가까운 값이 되므로, A = In + (1/k) Z의 행렬식을 구하는 과정에서
| Aiσ(i); σ(i) ≠ i | ≪ | Aii |
이 성립한다. 따라서 k가 충분히 크면 det A를 다음과 같이 근사할 수 있다.

k가 충분히 큰 경우 (1/k)이 곱해진 항보다 (1/k2), (1/k3), ···, (1/kn)이 곱해진 항이 훨씬 작아지므로 다음을 얻을 수 있다.

경우 2. tr(Z) = 0, Z112 + ··· + Znn2 > 0이라고 가정하면, 다음을 얻을 수 있다.

경우 3. tr(Z) = 0, Z11 = ··· = Znn = 0이라고 가정하면, 다음을 얻을 수 있다.
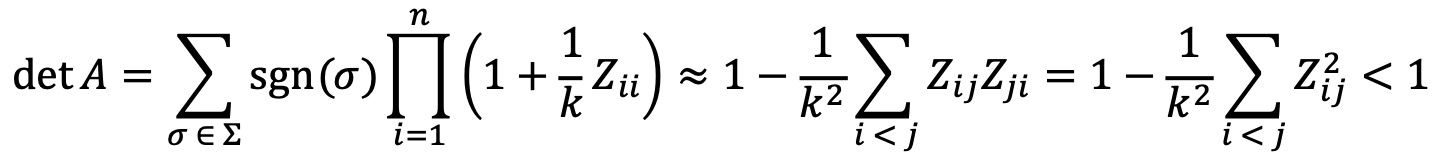
Z가 실대칭행렬이라는 조건은 경우 3에서 필요하다.
4. 다음 극한값을 구하여라.
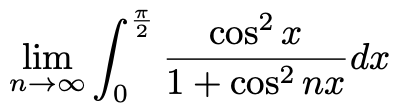
Solution.

5. 크기가 2020 × 2020인 행렬 A는 계수(rank)가 2이고, 모든 성분이 0 또는 1이다. 행렬 A의 성분을 모두 더한 값을 n(A)라 정의할 때, 가능한 n(A)의 값을 모두 구하여라.
Solution.
다음은 주어진 조건을 만족하는 상태에서 2 ~ 2019 × 2까지 모두 가능함을 보이고 있다. (3번째 이상 열을 1-2번째 열의 선형결합으로 나타냄)

다음은 주어진 조건을 만족하는 상태에서 2019 × 2 + 1 ~ 2019 × 3까지 모두 가능함을 보이고 있다.

이렇게 주어진 조건을 만족하는 상태에서 2 ~ 2019 × 2020까지 모두 가능함을 보일 수 있다.

위 예시에서 첫 번째 열을 두 번째 열에 더하여도 여전히 주어진 조건을 만족함을 보일 수 있다.

그런데 n(A) = 1이거나 n(A) = 20202인 경우 주어진 조건을 만족하지 않음은 자명핟.
따라서 2 ≤ n(A) ≤ 20202 - 1이 모두 가능하다.
6. 영역
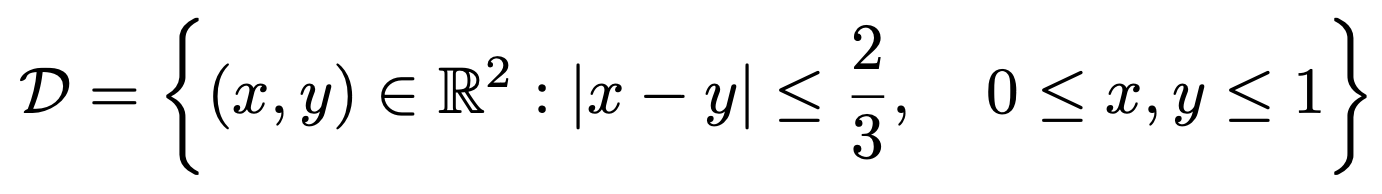
에 대하여 다음 적분값을 구하여라.
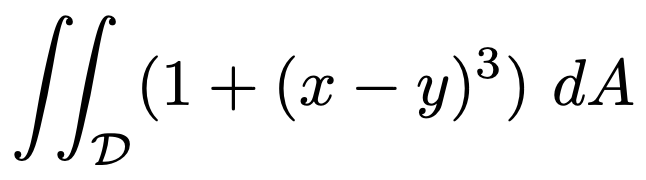
Solution.
영역 D를 도식화하면 다음과 같다.
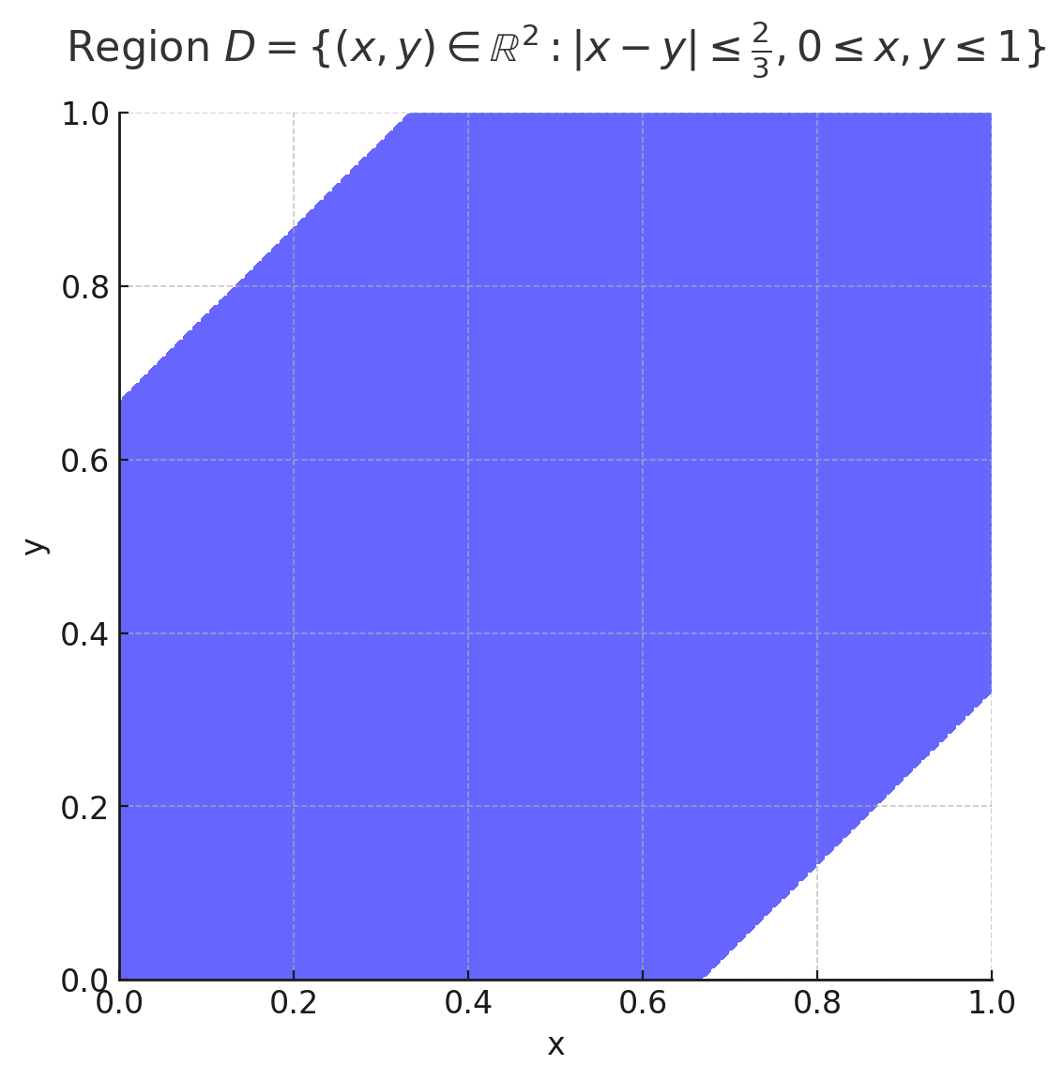
import numpy as np
import matplotlib.pyplot as plt
# Define the region D
x = np.linspace(0, 1, 400)
y = np.linspace(0, 1, 400)
X, Y = np.meshgrid(x, y)
# Condition for the region D
condition = np.abs(X - Y) <= 2/3
# Plot the region D
plt.figure(figsize=(6, 6))
plt.contourf(X, Y, condition, levels=[0, 0.5, 1], colors=['white', 'blue'], alpha=0.6)
plt.xlabel('x')
plt.ylabel('y')
plt.title(r'Region $D = \{(x,y) \in \mathbb{R}^2 : |x - y| \leq \frac{2}{3}, 0 \leq x, y \leq 1\}$')
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.grid(True)
plt.show()
따라서 준식은 다음과 같다.
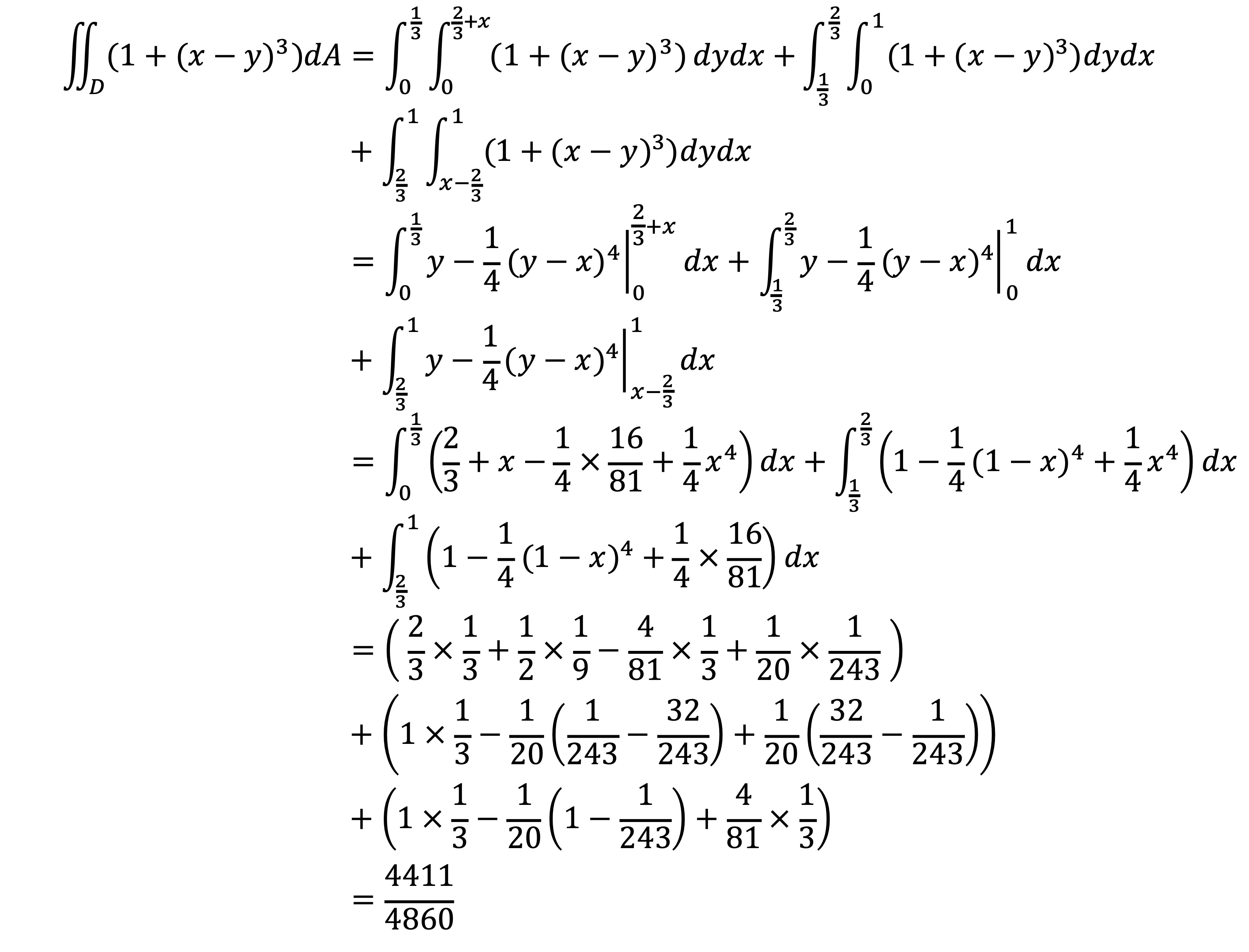
7. 두 번 미분가능한 함수 g : ℝ → (0, ∞)가 주어져 있다. 이계도함수 g"(x)가 모든 점에서 연속이고 g'(0) = g'(1) = 0을 만족하면, 다음 부등식이 성립함을 보여라.
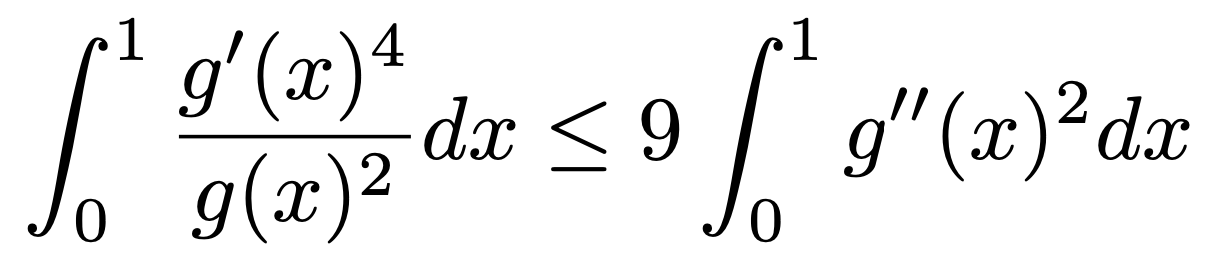
Solution.
절대부등식 0 ≤ (a-b)2 ⇔ 2ab ≤ a2 + b2 ⇔ 2ab - a2 ≤ b2 으로부터 다음 식을 구할 수 있다.

f2(x) = 3g''(x)라고 두면 다음을 얻을 수 있다.

g'(0) = g'(1) = 0으로부터 다음 식을 얻을 수 있다.

위 식에서 분모를 g(x)2으로 두면 (준식)에서 주어진 g'(x)4 / g(x)2와 비슷한 형태가 되므로 n=1로 두자.
따라서 준식을 증명하는 것은 f1의 존재성을 보이는 것과 동치이며, 다음과 같이 참이다.

8. 양의 실수열 {am,n}m≥0,n≥1이 모든 양의 정수 m, n에 대하여 다음 조건을 만족한다.
am+1,n × am-1,n+1 = am,n × am,n+1 - 1, a0,n = 1
양의 정수 m에 대하여 행렬 Bm = (bij)1 ≤ i,j ≤ m을 다음과 같이 정의하자.
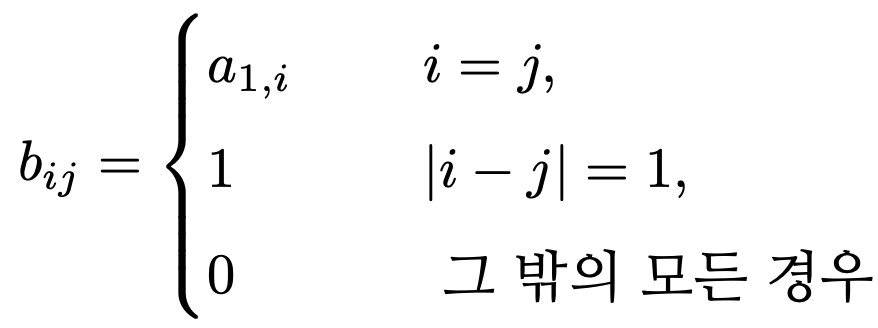
이때, 모든 양의 정수 m에 대하여 am,1 = det(Bm)이 성립함을 보여라.
Solution.
m = 1, 2인 경우, 주어진 정의에 의해 am,1 = det(Bm)임이 자명하게 성립한다.
여인수 전개에 의해 쉽게 다음이 성립함을 보일 수 있다.
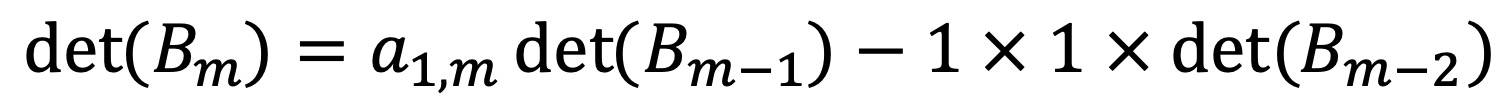
m = 1, ···, k일 때 am,1 = det(Bm)이 성립했다고 가정하자.
이제 (준식)을 증명하는 것은 다음 점화식(※)을 증명하는 것과 같다.

이 점화식을 증명하기 위해 주어진 점화식을 응용하자. 우선, 다음 식을 얻을 수 있다.
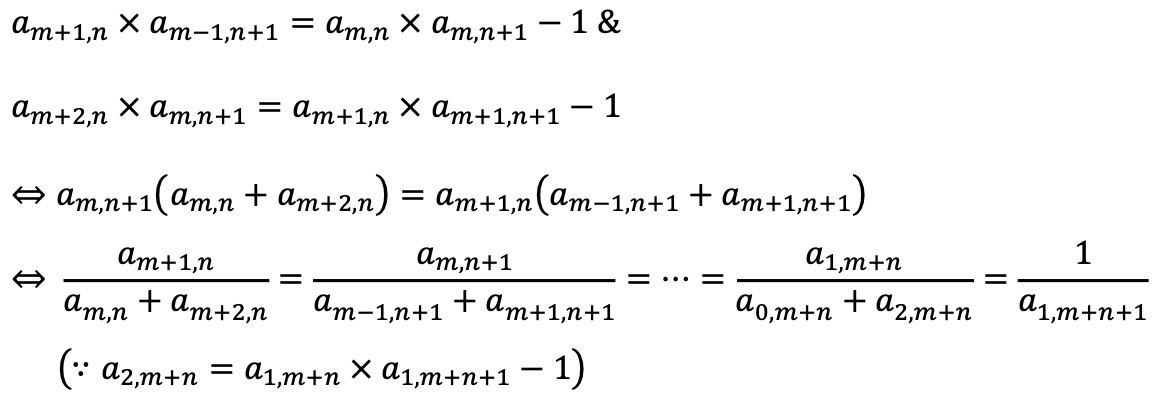
이때, am+1,n / (am,n + am+2,n) = 1 / a1,m+n+1에 m = k-1, n = 1을 대입하면 식 (※)을 얻는다.
입력: 2024.09.03 19:01
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2024.12.07 |
|---|---|
| 【대수경】 제 39회 전국 대학생 수학 경시대회 제 2 분야 (4) | 2024.12.06 |
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.04.06 |
| 【대수경】 제 40회 전국 대학생 수학 경시대회 제 1 분야 (1) | 2024.04.06 |
| 【대수경】 제 41회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.03.16 |




최근댓글